AutoBank软件分析河道堤防的渗流稳定性

(江西省赣抚平原水利工程管理局，江西 南昌 330096)

1 概 述

AutoBank软件是用于渗流计算和稳定性分析的重要软件，其研究对象为堤防、水库大坝等水工建筑物，它既能计算稳定渗流场问题，又能处理非稳定饱和渗流场的问题。AutoBank软件将三维的空间问题巧妙地简化为二维平面问题，其主界面是依托AutoCAD的界面设计的，使用者可以在界面中直接绘制简化模型。在构建模型时，使用者应定义其宽度、高度、边坡比等，确定土层的材料和渗透系数，绘制出临界水位的高度，根据这些数据AutoBank软件利用有限元的原理进行渗流计算，求解渗流场，并将渗流场的计算结果以图表或数值的型式直观显示出来，包括等势线、浸润线、流速等值线图、流速矢量图、水力坡降等值线图等[1]。

本文以江西省抚河河道为研究对象，防渗材料采用钠基膨润土防水毯，利用AutoBank软件进行渗流计算，分析其实际的作用效果。

钠基膨润土防水毯是新型的复合材料，是由两层土工合成材料夹封膨润土，利用针刺、黏结或缝合工艺等制作而成的，其中起防水作用的主要成分为蒙脱石[2]。在遇水情况下，膨润土颗粒会迅速膨胀，挤压颗粒间存在的空气，形成一层致密的不透水层，从而起到挡水作用。通常可将膨润土防水毯分为三种型号(见图1)[3]。

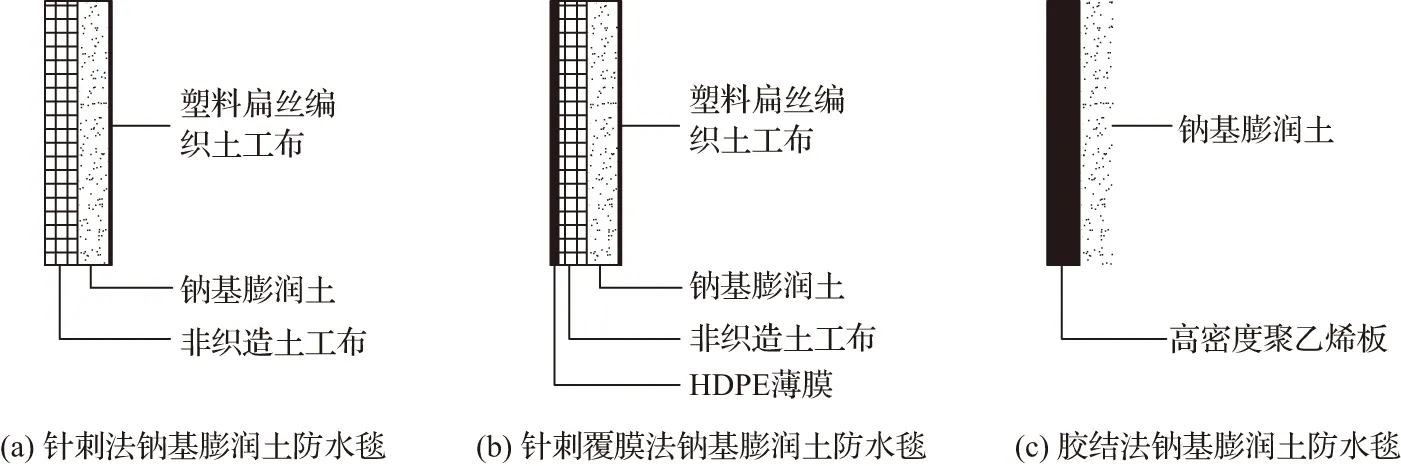
图1 钠基膨润土防水毯的分类

2 防水毯的渗透系数

作为复合材料，钠基膨润土防水毯的渗透系数并不是固定不变的，而是随水头的变化而变化。张潮等[2]建立了钠基膨润土防水毯的室内试验模型，测得其渗透系数与水头成非线性关系：y=6.97x-0.49，其相关系数为R=-0.9481。即水头越高，防水毯的渗透系数越小，其防渗效果越优越。根据实际情况，抚河河道水深最深为2.2m。本文选取0.50m、1.00m、1.50m、2.00m四种水头，利用AutoBank软件分析在四种水头作用下的钠基膨润土防水毯的防渗效果。在以上四种水头作用下，求得钠基膨润土防水毯的渗透系数(见表1)。

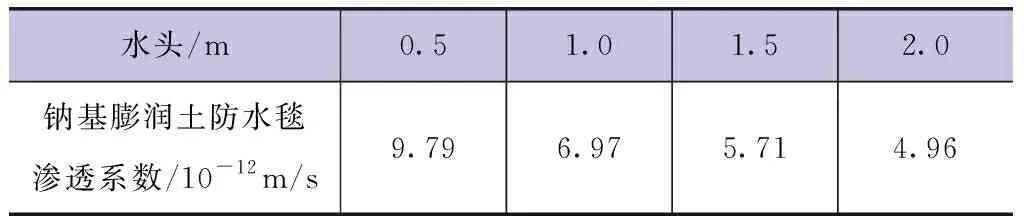
表1 钠基膨润土防水毯的渗透系数

3 渗流计算

3.1 AutoBank计算流程

利用AutoBank软件进行渗流计算首先要对所选取的断面进行基本假定，将复杂的工程问题简化为可数据量化的模型(见图2)。其假定为：渗流服从达西定律；河道足够长，具有相似性，故将三维空间问题转化为二维平面，按照平面问题处理；保护层与防水毯间完全结合，不存在空洞或缝隙；防水毯平整均匀，渗流系数固定不变。

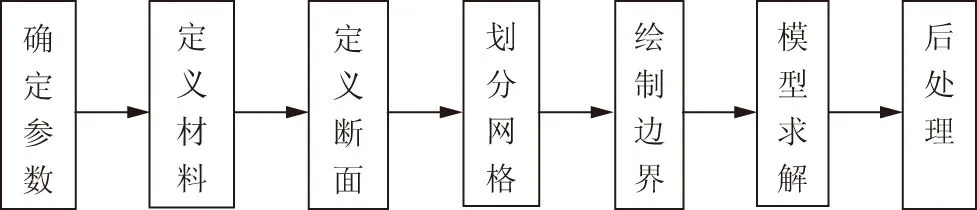
图2 有限元模型建立流程

软件的应用按以下步骤进行：

a.打开软件，进入主界面。

b.构建简化模型。定义模型的长度、宽度、高度及边坡比，绘制断面的简化模型，注意模型应闭合。定义不同的土层名称和渗透特性，由于假定抚河河道为稳定渗流，则只需定义土层的渗透系数，并利用不同的颜色对土层加以区分。

c.单元网格划分。AutoBank软件包括两种网格划分方式，此次计算利用全自动划分方式，将模型分为若干个矩形小单元。

d.定义边界条件。这是渗流计算的依据，边界条件包括固定水位边界和可能出逸边界等，与水接触位置为固定水位边界，在水位以下且不与水接触位置为可能出逸边界。

e.求解。利用渗流计算模块对模型进行求解，将所求解的渗流场进行输出和生成。

f.后处理。对输出的渗流结果进行分析，总结其单宽渗流量和水力梯度的分布规律。

3.2 计算原理

抚河河道长度较长，流域内流速区域稳定，因此可将其看作稳定的均匀渗流，符合达西定律。软件依据的计算公式为

该公式应用的控制条件为

式中h0——边界水头；

n——边界外法线方向；

z——浸润线上各点的几何纵坐标值。

3.3 断面选取

抚河河道线路较长，可以只取一横截断面进行分析计算。由于河道的左右岸为中轴线对称分布，且河道较宽，如果取用整个过水断面，则河道高度与宽度差距过大，并不能在同一界面以同一比例尺表示，所以为使模型更加直观，求解结果更明确，此次渗流计算只取河道一侧进行简化(见图3)，选取1号断面作为典型断面。

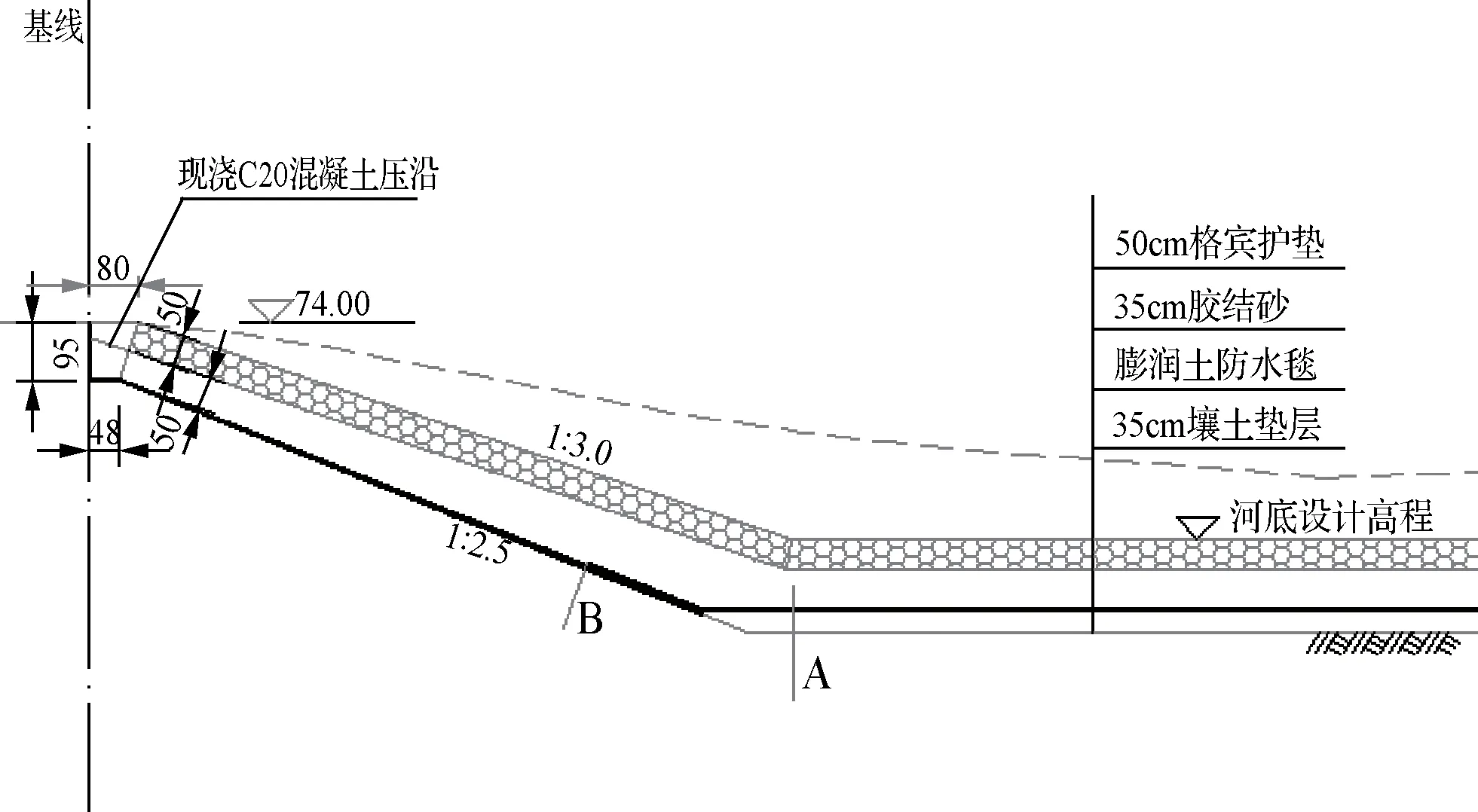
图3 1号水面断面(尺寸单位：cm)

3.4 建立计算模型

根据断面结构型式以及AutoBank软件的计算对象等情况，对所选断面进行合理的简化。由于壤土层上部的格宾石笼只用于固定和压实壤土，避免壤土被水流冲刷影响防水毯的效果，并没有起到实际的防水效果，因此其在简化断面中并不体现。在此简化模型中，只需将起到防渗作用的土层进行定义，包括壤土层和防水毯层。简化后的几何模型如图4所示。

图4 简化后断面几何模型

3.5 确定边界条件

一般来讲，模型的边界条件主要包括模型的几何参数以及边界上起支配作用的条件。从描述流动的数学模型看，边界条件主要包括两种形式：固定水位边界条件和出逸边界条件。

以1.50m水头条件下的模型为例，其边界条件如图5所示。

图5 1.5m水头作用下的断面边界条件

3.6 网格划分图

网格划分的前提是计算区域为闭合性的，此次网格划分选取全自动的方式，划分网格后的模型如图6所示。

图6 1.5m水头作用下的断面网格划分

4 防渗效果分析

4.1 单宽渗流量

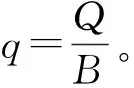
根据AutoBank软件的计算输出结果，不同水头作用下的单宽渗流量不同，具有一定的变化规律(见表2)。

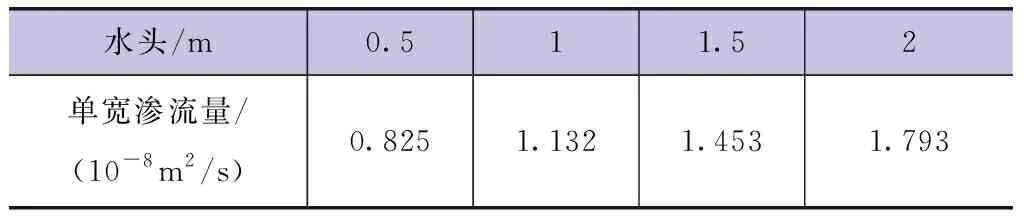
表2 单宽渗流量

以水头为X轴，对应的单宽渗流量为Y轴，画出两者之间的关系曲线(见图7)。

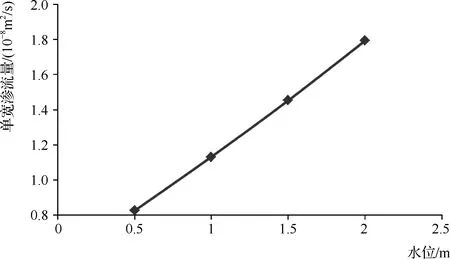
图7 单宽渗流量变化曲线

图7直观体现了防水毯的单宽渗流量随水头的变化趋势。由图7的变化曲线可知，不同水头条件下，防水毯的单宽渗流量也不相同，后者随水头的增大而增大。分析变化趋势可知，由于水头的增加，使得防水毯承受的水压变大。尽管钠基膨润土防水毯的渗透系数随水头升高而降低，但由于所受压力变大的影响，使得防水毯的渗透水量随之增大，导致单宽渗流量变大。

4.2 浸润线

浸润线是指渗流在断面内的自由面与横剖面的交线，即浸润面与横剖面的交线[4]。浸润线可以直观体现土体中渗流水的自由表面所处位置。确定浸润线的位置，就可以判断堤防、大坝等建筑物的渗流是否具有稳定性，从而确定水工建筑物是否安全。利用AutoBank软件能够直观显示不同水头作用下模型的浸润线所处位置，据此可以对防水毯的作用效果进行直观的评价。不同水头条件下的浸润线位置见图8。

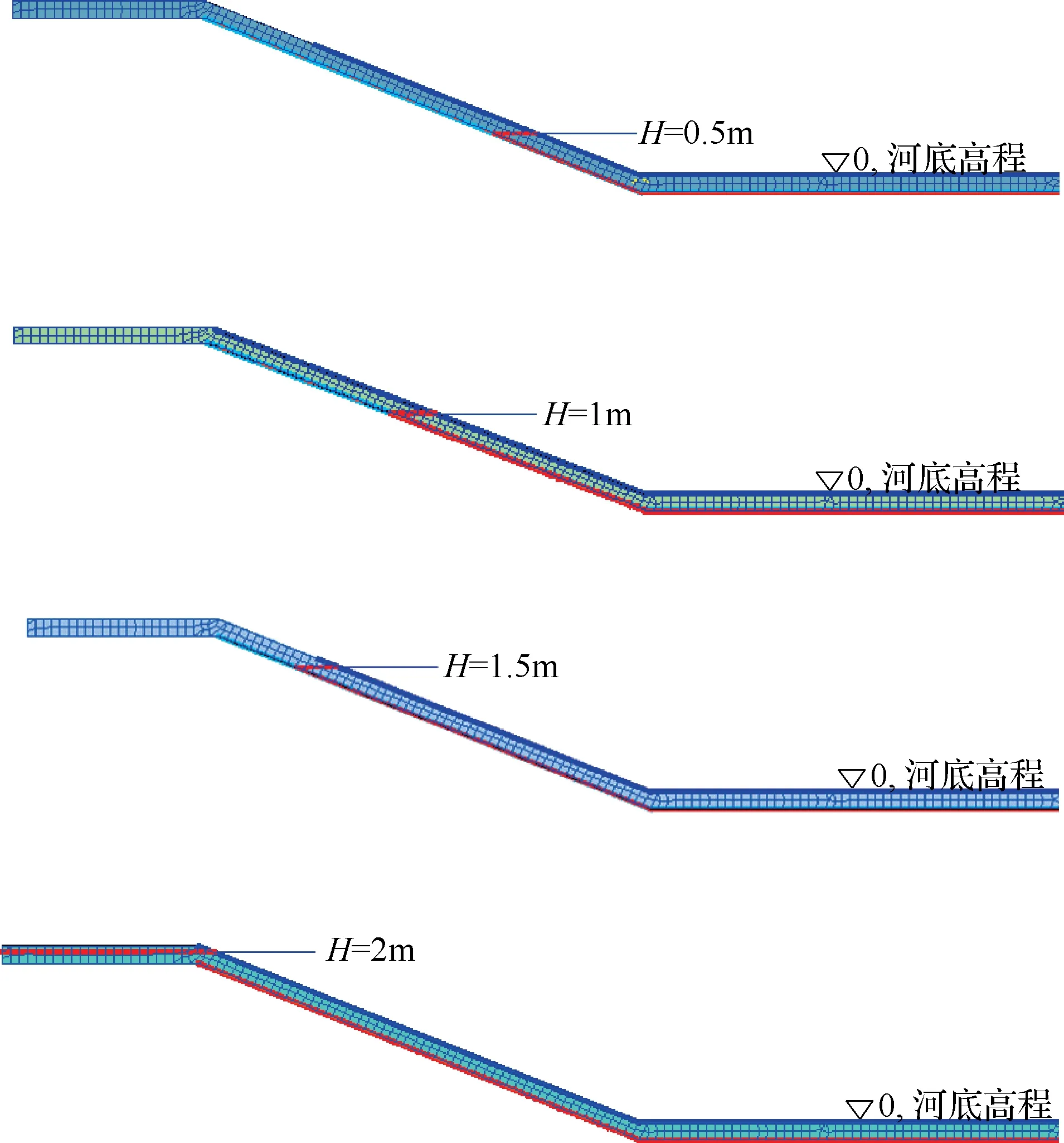
图8 不同水头作用下断面的浸润线

由图8可知，不同水头条件下的浸润线具有一定的相似性，其位于保护层(即壤土层)以内，防水毯层以上。浸润线的高度与自由水面基本持平。防水毯所承受的水头越大，则其渗流路径就越长。

根据以上4种水头条件下浸润线的位置分布规律可以看出，防水毯层起到了十分显著的防渗作用，能够做到少透水甚至不透水，使得河道堤防中渗流非常稳定。可以确定，抚河的河道堤防安全性得到了保证。

4.3 水力梯度

水力梯度是指沿渗透路径水头损失与渗透路径长度的比值，反映了渗流沿水流方向在每单位距离上的水头下降值，也可理解为渗流通过单位长度渗透途径时，克服摩擦阻力所耗失的机械能[5]。

以1.50m水头条件下的模型为例，求解的最大水力梯度值为57.14，位于坡脚处，该处距自由水面最远；水位差沿断面边坡越来越小，使得水力梯度逐渐降低，到达自由水面处达到最小值，为3.18；河道底部水力梯度值与坡脚位置相同。这是因为，坡脚处为距自由水面线垂直距离最大的位置，而在自由水面线处其距离最小。渗流路径指的是渗透水经过保护层到达防水毯层的距离，这是一定值，即为保护层的厚度。

根据浸润线的绘制图形可知，模型的渗透路径就是保护层表面到防水毯表面的垂直距离，即保护层的厚度，该数值是固定不变的。因此，水头越大，对防水毯的压力越大，产生的水力梯度也随之变大。

现对不同水头作用下的最大水力梯度值进行对比分析，其变化曲线见图9。

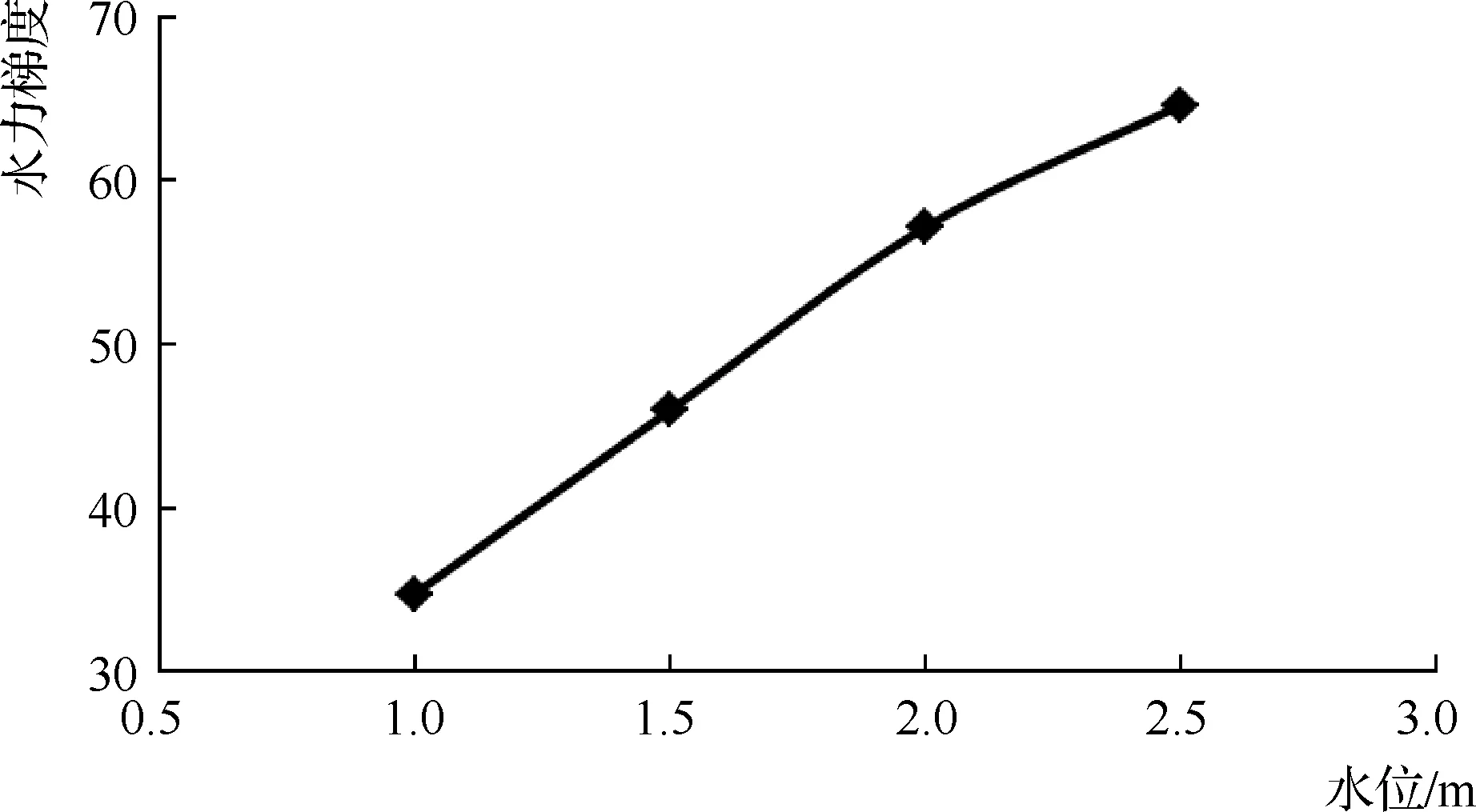
图9 不同水头作用下的断面水力梯度分布

从图9可看出，随着水头的逐渐增加，各断面的最大水力梯度值也逐渐变大。根据浸润线的变化规律可知，由于水头的增加，模型渗流途径变长，其水头损失的最大值也变大，最大水力梯度值随之变大。

4.4 分析结论

对AutoBank软件所求解的渗流场输出结果进行分析，可以总结出以下结论：

a.随着水头的逐渐增加，单宽渗流量逐渐变大。

b.不同水头条件下的浸润线延伸方向具有一定的相似性，其位于保护层(即壤土层)以内，防水毯层以上。浸润线的高度与自由水面基本持平。防水毯所承受的水头越大，则其渗流路径就越长。

c.在河道边坡范围内，水力梯度最大值位于河道断面的坡脚位置，沿断面边坡向上逐渐减小，在水位线处，水力梯度最小；河道底部水力梯度值与坡脚位置数值相同。

d.随着水头的逐渐增加，各断面的最大水力梯度值也逐渐变大。

5 结 语

本文利用AutoBank软件，对抚河河道堤防进行简化，建立计算模型，求解模型的渗流场，根据单宽渗流量、水力梯度及浸润线的输出数据，对钠基膨润土防水毯的实际效果进行评价，判断堤防的稳定性。计算结果表明:钠基膨润土防水毯具有显著的防渗作用，抚河河道堤防十分稳定。