基于希尔伯特—黄变换的控制阀气密性故障诊断研究

,,,

(浙江工业大学 信息工程学院，杭州 310023)

0 引言

控制阀作为工业控制系统的重要和关键组成部件，工业过程控制的性能很大程度上受其影响。而气动调节阀作为其中的佼佼者，应用最为普遍。薄膜气动控制阀的主要动力和控制源自于空气压缩机提供给薄膜气室的空气。通过智能阀门定位器控制薄膜气室的气压，从而推动阀杆克服弹簧弹力和摩擦力上升或者下降；最终通过连接阀杆的阀芯来控制流经阀体节流面介质的流量大小。然而气路漏气的发生会导致控制阀直接失去动力源，使阀杆不能精确的响应设定信号，轻则影响产品性能工艺，重则造成设备和人员的损坏和伤亡[1]。所以及时诊断出控制阀运行过程中的故障并且保证控制阀的正常平稳运行，成为科研工作者研究的重中之重。

气密检测是衡量许多工业品密封性能的重要手段[2],然而国内对于气密性检测技术的研究相对落后，传统上主要依靠人的主观感官去判断，不确定因素较大。目前国内外较为常用的干式漏检法为差压漏检法[3]，虽然应用广泛，但也存在很多问题比如使用寿命和检测精度等[4]，而基于信号处理分析的方法具有操作方便、精度高的优点。

1998年美国国家宇航局Huang等人提出了一种新的信号分析理论希尔伯特-黄变换(Hilbert-Huang Transform简称HHT)[5]，它包括经验模态分解(Empirical Mode Decomposition简称EMD)和Hilbert变换(HT)两个主要步骤。 HHT是一种有效分析各类信号的时频分析方法。基于信号的自适应特性和局部特征，解决了傅里叶变换不能有效处理的非线性、非平稳信号的难题。针对控制阀的相关信号的特征提取，有效刻画了控制阀阀位响应信号的相关特性。然而在HHT方法问世之后Huang及以后的研究者多应用于地震、声学、地球物理学、海洋学、电机、齿轮、轴承等方面[6-8]。但是在气动控制阀诊断应用领域的研究却相对较少。

本研究将希尔伯特黄变换方法引入到气动控制阀气室气密性故障诊断研究中，模拟了气室漏气，采用EMD对阀位信号进行分解，实现了对故障发生时刻的检测，计算模态能量值，通过对比控制阀是否漏气状态下的模态能量值达到了对故障的强度识别。

1 希尔伯特-黄变换算法

希尔伯特-黄变换由两个部分组成：首先是用经验模态分解(EMD)方法分解已采集到的初始信号X(t),分解并提取原信号中固有IMF分量; 每个固有模态函数理论只含单一频率的信号成份[8]。其次对于每个模态，作Hilbert变换，获得其表征频率、时间和幅值的希尔伯特谱H(ω,t)，通过对其积分获得希尔伯特边际谱h(ω)，从而得到信号分析处理的结果。该方法的简要流程如图1所示。

图1 Hilbert-Huang变换框图

1.1 经验模态分解(EMD)

Huang[9]详细的介绍了HHT的相关理论，该算法采用经验模态分解(EMD)解决了信号自适应分解的难题。EMD将给定连续信号X(t)自适应的分解为一个残余项及多个固有模态函数。

图2 EMD分解流程图

通过如图2所示的EMD分解流程框图即可得到各个固有模态分量；信号分解提取模态如下式，等号左边是原始信号X(t)，经EMD分解得到等号右边IMF分量的累加及剩余分量r(t)。即：

(1)

式中，n为信号分解所得IMF的个数，r(t)是此分解过程最终产生的剩余分量。

从图2的EMD分解流程图及(1)式可知第i个IMF与第i-1个相比有着较低的频率分布。即IMF分量的频率从高到低依次生成；不同的IMF代表着不同的时间尺度对应的原始信号特征[10]。剩余分量r(t)代表着X(t)原始信号的整体趋势，在诸如海洋、气候等缓慢变化的信号中有着及其重要的利用价值。但是对于控制阀气室漏气造成的气压突变信号中，通常被去掉不用。

1.2 Hilbert变换(HT)

长期以来，采用傅里叶变换处理从时域变换到频率域上信号有着明显的效果，但是针对非平稳信号中存在的特殊频率成分，傅里叶变换的结果是该频率在此序列内一直存在。而Hilbert变换可以将时域信号X(t)变换到相同域的信号y(t)。这一时频分析方法被广泛的应用在许多实际信号的分析处理中。例如在声纳、雷达、地震信号、机械振动信号的应用中，验证了Hilbert变换在处理此类特征信号方面的有效性和优越性。

希尔伯特变换由德国数学家Hilbert提出来的，对于X(t)在区间(-∞，+∞)的实函数，其希尔伯特变换交换定义为：

(2)

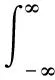
(3)

其中:P为柯西主值，y(t)为给定信号序列X(t)的Hilbert变换，本质上是将Hilbert变换定义为给定信号X(t)与时间倒数的卷积，它强调了X(t)的局部特性。作为现代信号处理准则的基础之一，由实信号向复信号进行扩展[11]。因此，z(t)可被定义为复解析信号：

z(t)=x(t)+iy(t)=a(t)ejθ(t)

(4)

式(4)能有效的确定相关变量，以上定义时频表达式的基础，且更适用于分析信号频带宽度与信号持续时间相乘足够大的情况。

1.3 模态能量

模态能量法可以用来判断各阶模态频率下，模态能量在系统各个自由度分布。从能量这一重要特征信号，研究控制阀及其相关附件的故障类型特征。因此作为研究诊断控制阀薄膜气室漏气故障的重要方法。首先提取控制阀阀杆位置响应信号的能量特征，然后构建对应的特征向量。经验模态分解将原始信号分解成若干个不同频段范围的模态分量，当出现漏气相关故障时，不同频率范围的阀位响应信号相较于不漏气时会发生变化，从而引起相应频段内的能量变化。因此[12]，分别提取不漏气时信号与漏气时信号对应模态能量进行对比,构建阀位响应信号的能量特征。由此定义控制阀阀位响应信号能量为：

(5)

同时，待检测信号与气密性良好状态下的阀位响应信号的模态分量的能量比为：

(6)

式中,δ表示待测阀位响应信号的能量特征，ej表示漏气状态下阀位响应信号IMF分量的能量值；Ej表示正常状态下的阀位响应信号IMF分量能量值。

2 仿真分析

在控制阀故障诊断MATLAB/Simulink模型中进行仿真分析,模拟膜头穿孔导致的气室气密性故障，文献给出了其数学表达式如下：式中Ps为气室气压，fs为故障强度[13]。

Psf=Ps(1-0.5fs)fs∈(0,1)

(7)

为了更好模拟控制阀在实际工业生产中的状态，保证能够实现在线应用,本次选择的随机信号必须满足控制阀实际工况，因此所用随机信号其频率设定不能超过待测阀的截止频率(0.22 Hz)，时间在400 s以内。仿真所用的正弦设定信号均为：

y=50+20*sin(2*pi*0.05*t)+25*sin(2*pi*0.1*t)，t∈(0,400s)；

2.1 EMD经验模态分解

2.1.1 正弦信号测试

故障发生时间：160 s

故障强度：0.1

图4 EMD分解结果

2.1.2 随机信号

故障发生时间：200 s

故障强度：0.2，如图5～6所示。

图5 随机信号及阀位

图6 EMD分解结果

2.2 Hilbert变换故障诊断

2.2.1 正弦信号测试

(1)故障类型：无(正常状态)

故障强度：0，如图7所示。

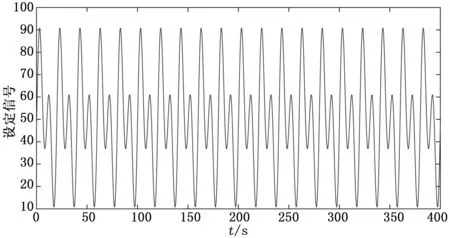
图7 多正弦设定信号

对于上述信号，经过模态分解后，前两个模态的能量占比如图8所示。

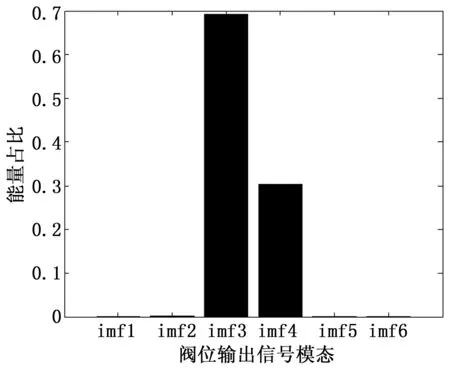
图8 正弦信号正常状态阀位模态

(2)故障类型：气室漏气

故障强度：0.1(微弱)

故障开始时间：160 s

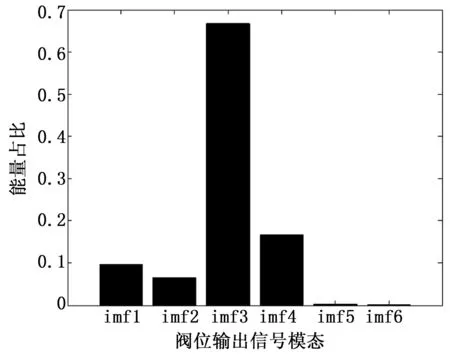
图9 气室漏气故障微弱状态阀位模态

(3)故障类型：气室漏气

故障强度：0.3(较弱)

故障开始时间：60 s

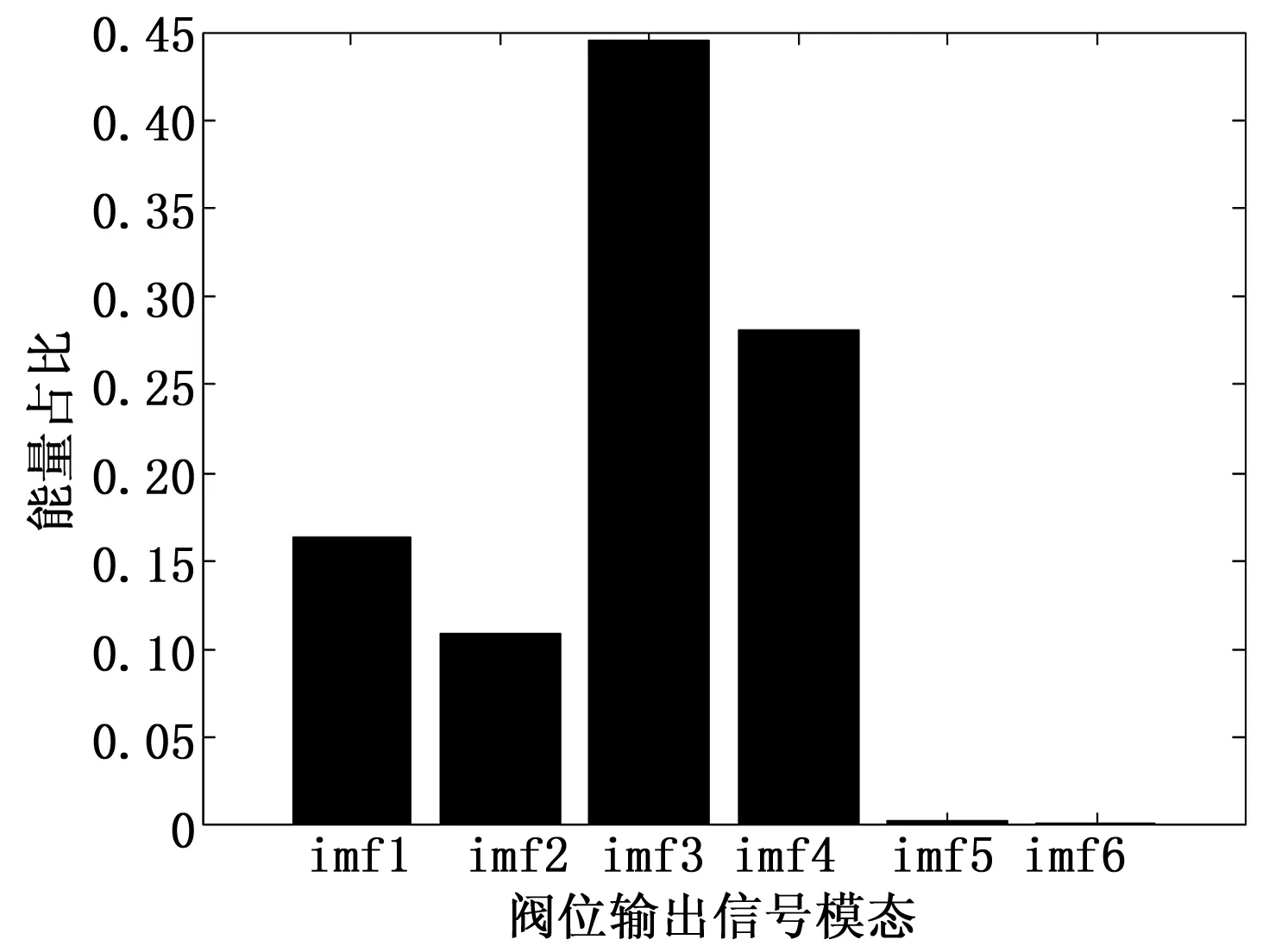
图10 气室漏气故障较弱状态阀位模态

此设定信号下的前两个模态能量占比之和与故障强度的趋势如图11所示。

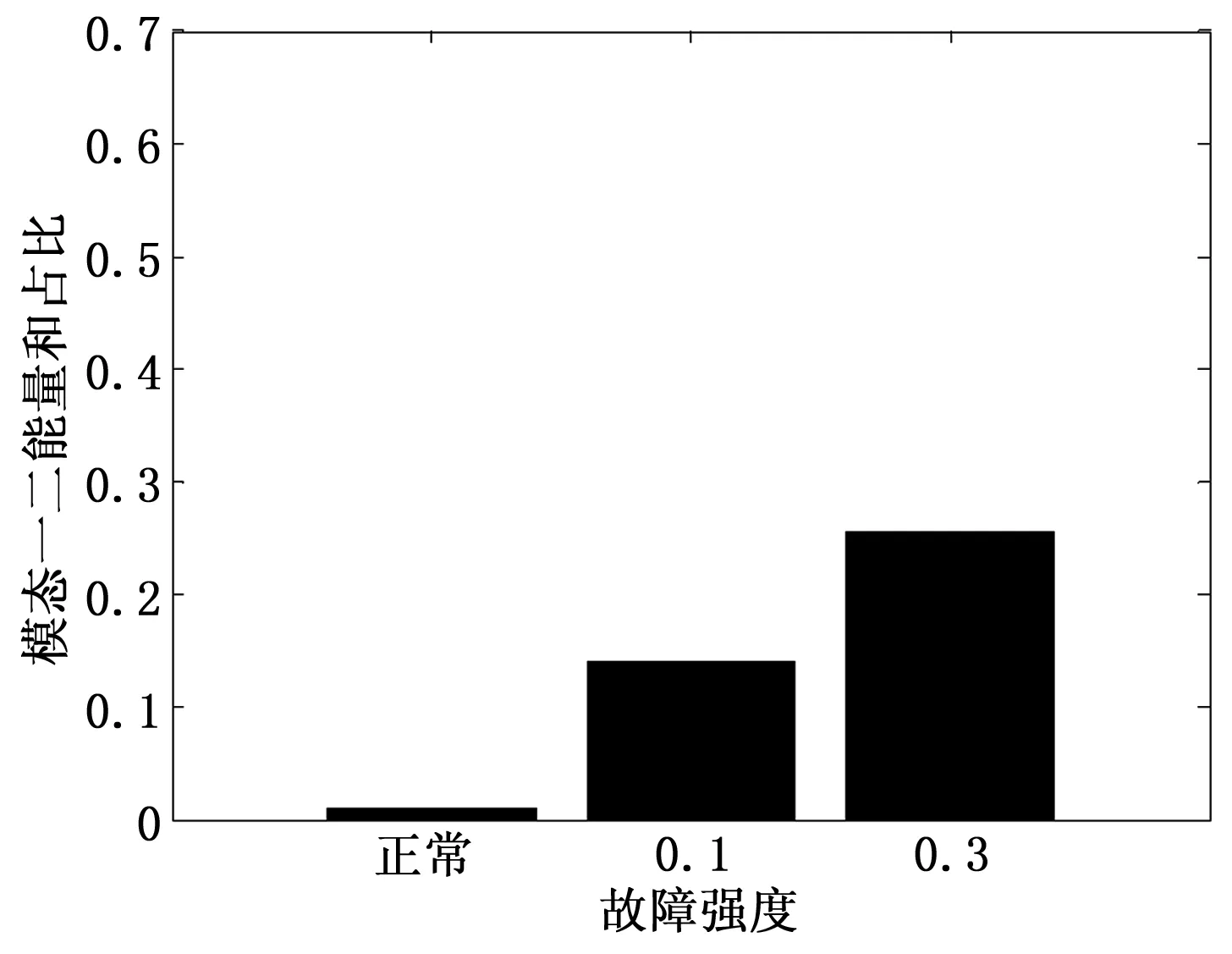
图11 模态一、二能量和占比与故障强度的趋势图

2.2.2 随机信号测试

(1)正常状态测试

故障强度：0，如图12～13所示。

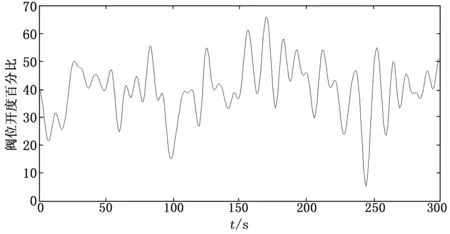
图12 随机信号

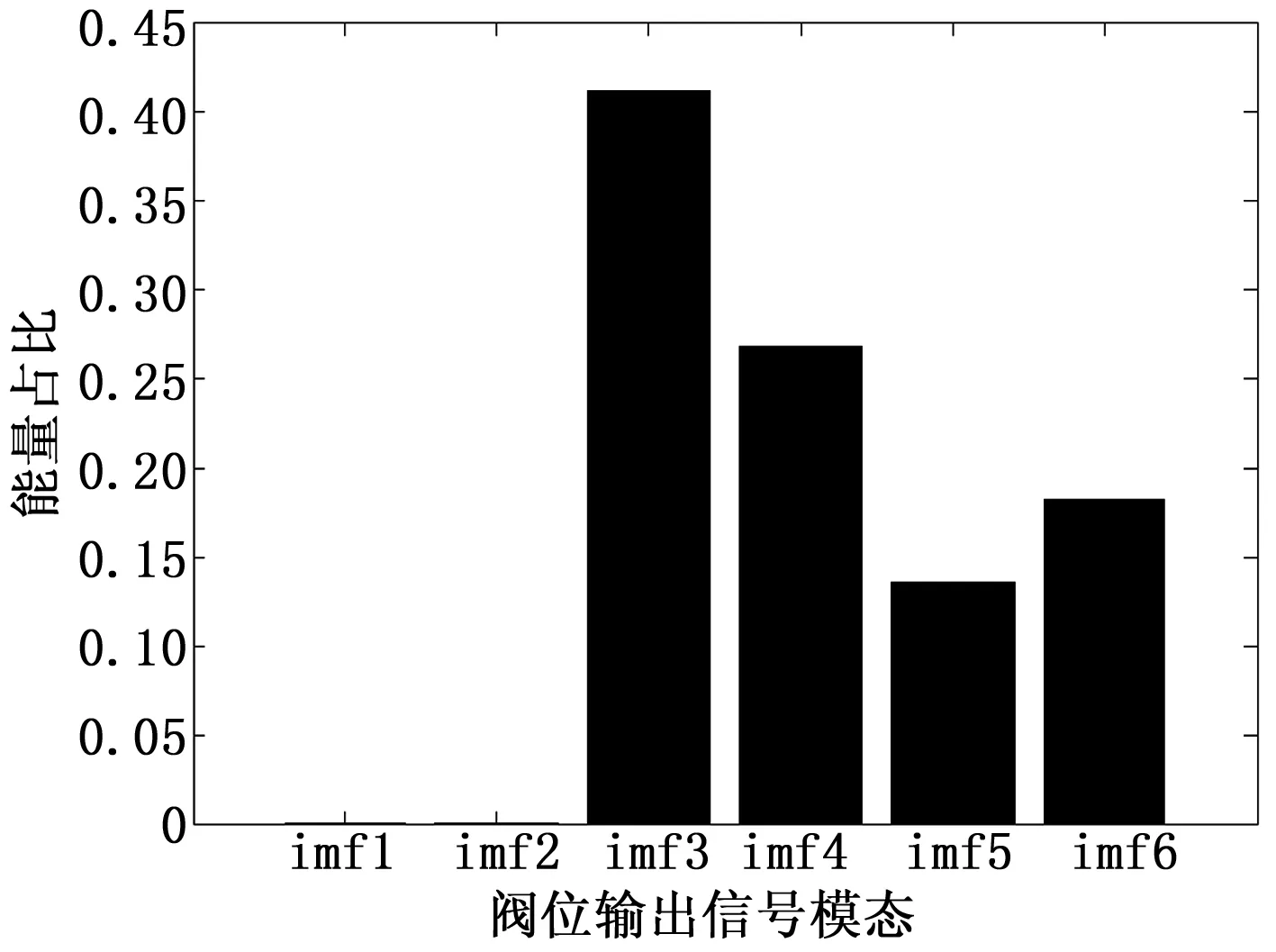
图13 随机信号正常状态阀位模态

(2)故障测试

故障强度：0.1(微弱)，如图14所示。

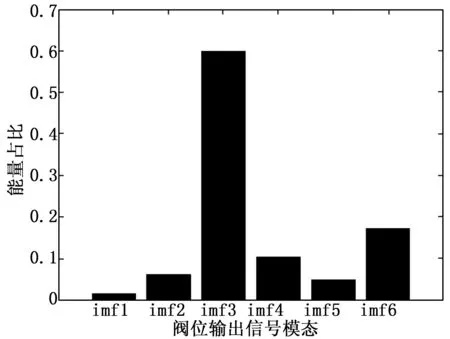
图14 气室漏气故障弱状态阀位模态

(3)故障测试

故障强度：0.3(较弱)，如图15所示。

图15 气室漏气故障较弱状态阀位模态

该随机信号下的前两个模态能量占比和与故障强度的趋势如图16所示。

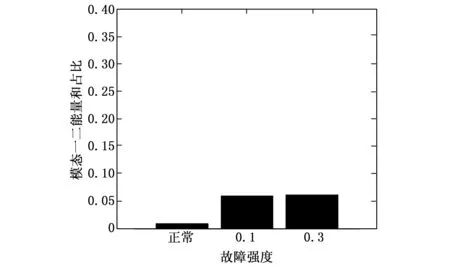
图16 模态一、二能量和占比与故障强度的趋势图

从仿真结果可以看出，在Simulink搭建的控制阀故障诊断模型中,通过希尔伯特-黄变换的方法能够有效分析各阶模态及其能量占比特性，获得了控制阀气室气密性故障、故障强度的诊断。

3 实验平台与实验方案

3.1 实验平台

3.1.1 硬件实验平台介绍

搭建控制阀气室气密性故障检测硬件实验平台如图17所示。

图17 执行器故障诊断系统实验平台

其中1空气压缩机，2减压阀，3稳压电源，4机箱和板卡的组合，5压力传感器，6薄膜气动控制阀，7智能阀门定位器，8三通阀和小型手阀， 9上位机及LabVIEW程序。

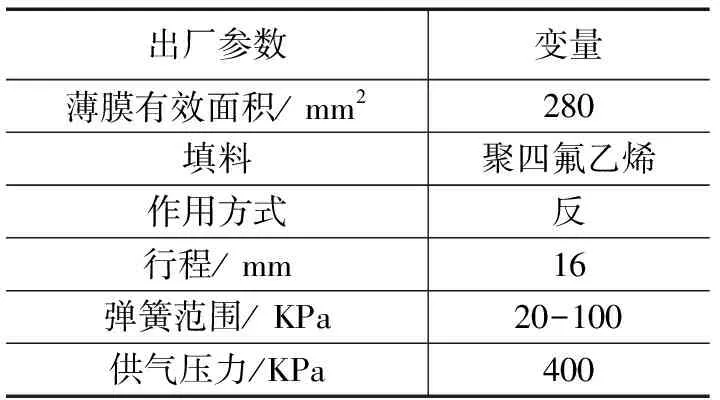
表1 实验用控制阀的出厂参数

3.1.2 LabVIEW软件介绍

实验所用软件由美国国家仪器(NI)公司研制，使用图形化编辑语言G编写程序，实现了对控制阀设定信号的发送、数据采集、报表生成、数据存储的功能，如下图所示此VI项目主要实现了对控制阀设定信号SP,阀位响应信号PV，气室气压信号P2,气源气压信号Ps，通过转换将设定信号SP及阀位响应信号归一化至0—100的区间。LabVIEW程序由上位机操控实现对硬件平台的有效控制。

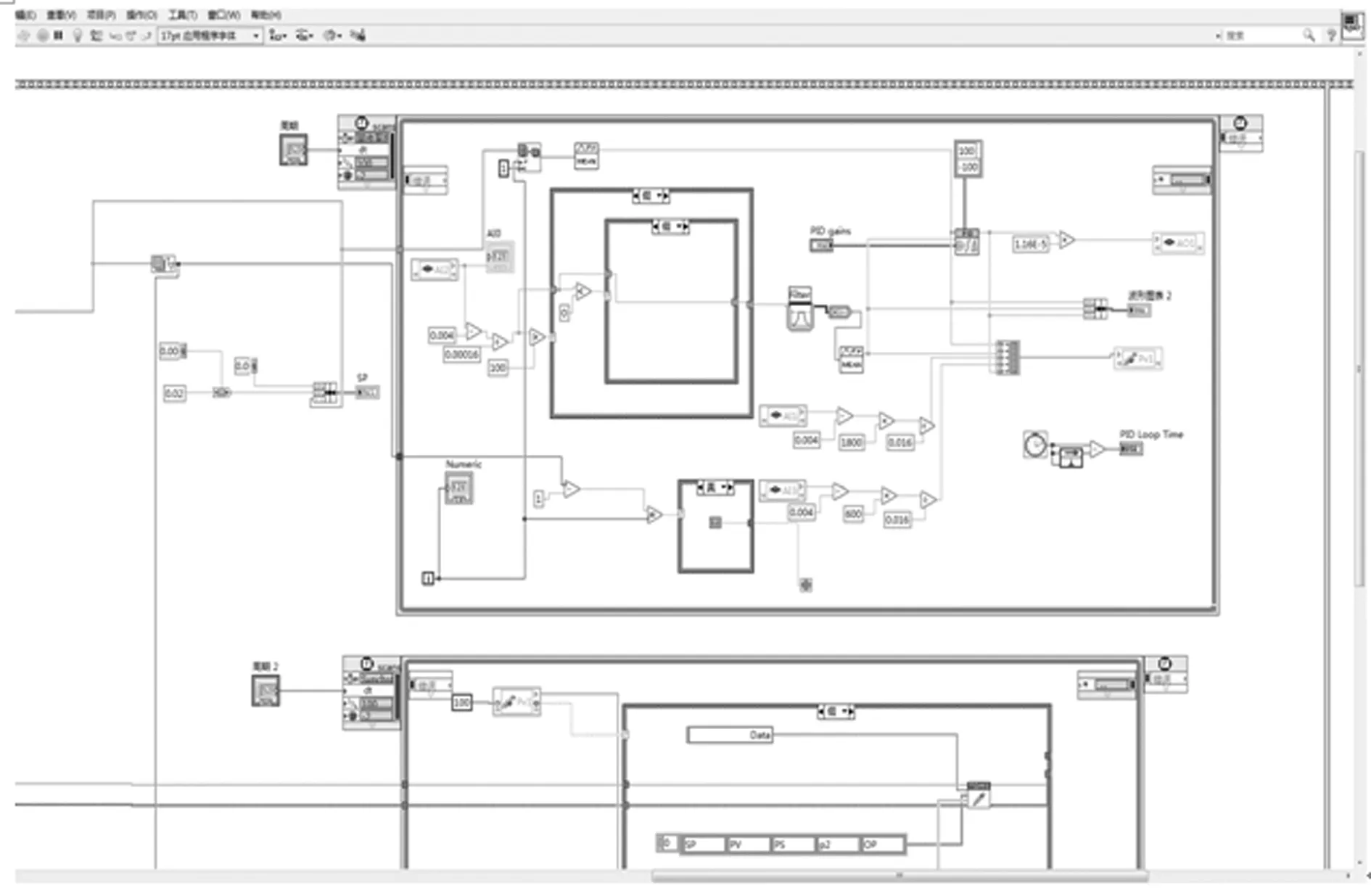
图18 LabVIEW程序框图后面板

3.2 实验方案

实验模拟气动调节阀常见的气密性故障，例如接头、气管损坏或者螺栓松动、薄膜穿孔等常见故障类型。此故障发生时会引起薄膜气室气压的瞬间波动，进而导致对对阀杆的振动冲击。最终引起高频模块振动加剧，作为高频成分的前两个模态能量便会相应的变多。

实验操作步骤如下：

1)首先，按照图17所示硬件实验平台，连接电路和气路，通过上位机LabVIEW程序经NI板卡给智能阀门定位器发送不同的设定信号SP。

2)其次，在控制阀跟随设定信号开始正常动作后，选定时刻将图17第8个部件对应的小型手阀旋开一定圈数。来模拟薄膜气动调节阀的气密性故障。

3)程序跟随设定信号运行完毕，此时将小型手阀旋紧恢复到实验最初的旋紧状态。

4)循环前3个步骤，同时旋开小型手阀至其他开度，模拟薄膜气动调节阀气密性故障的另一种强度。

5)处理数据，利用MATLAB工具将数据导入希尔伯特-黄变换的算法程序中，加入经过EMD经验模态分解，选出与阀位响应信号系数最相近的6阶模态用于作出模态能量图的展示。

4 实体阀实验分析

为了验证该方法在实体阀工作中监测性能的有效性，对控制阀设置了不同的阀位信号和故障强度，模拟了不同强度的气室漏气故障。所用随机阀位设定信号均满足频率和时间如下,f∈(0,0.22 Hz),t∈(0,400 s)。 此次所用设定正弦信号为：y=50+10*sin(2*pi*0.02*t)

4.1 EMD分解故障检测

4.1.1 正弦信号测试

故障程度:小型手阀松6圈，故障发生时刻:205秒，如图19～20所示。

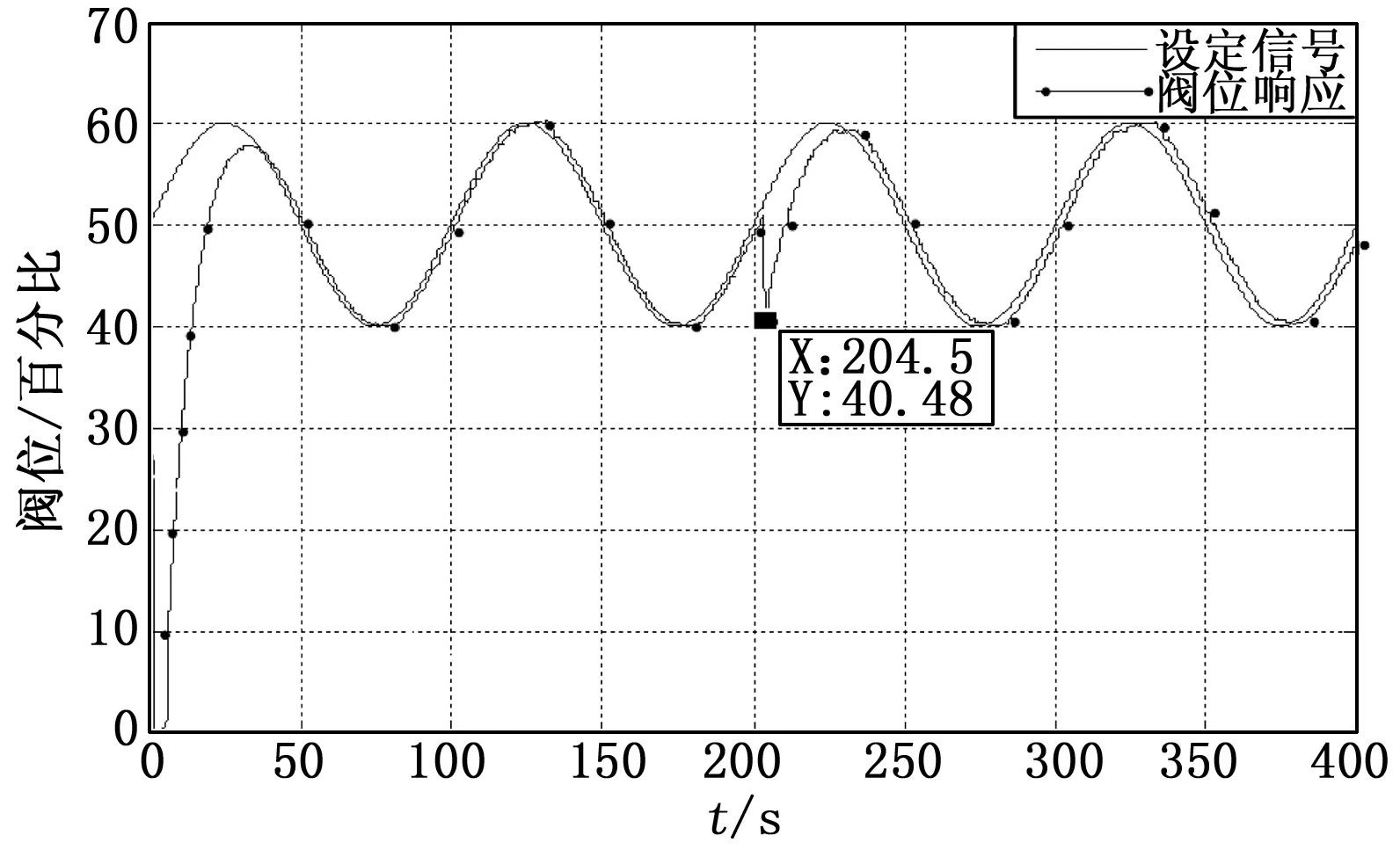
图19 阀位响应曲线

图20 EMD分解结果

4.1.2 随机信号测试

故障强度:小型手阀松4圈，故障发生时刻:230秒，如图21～22所示。

图21 阀位响应曲线

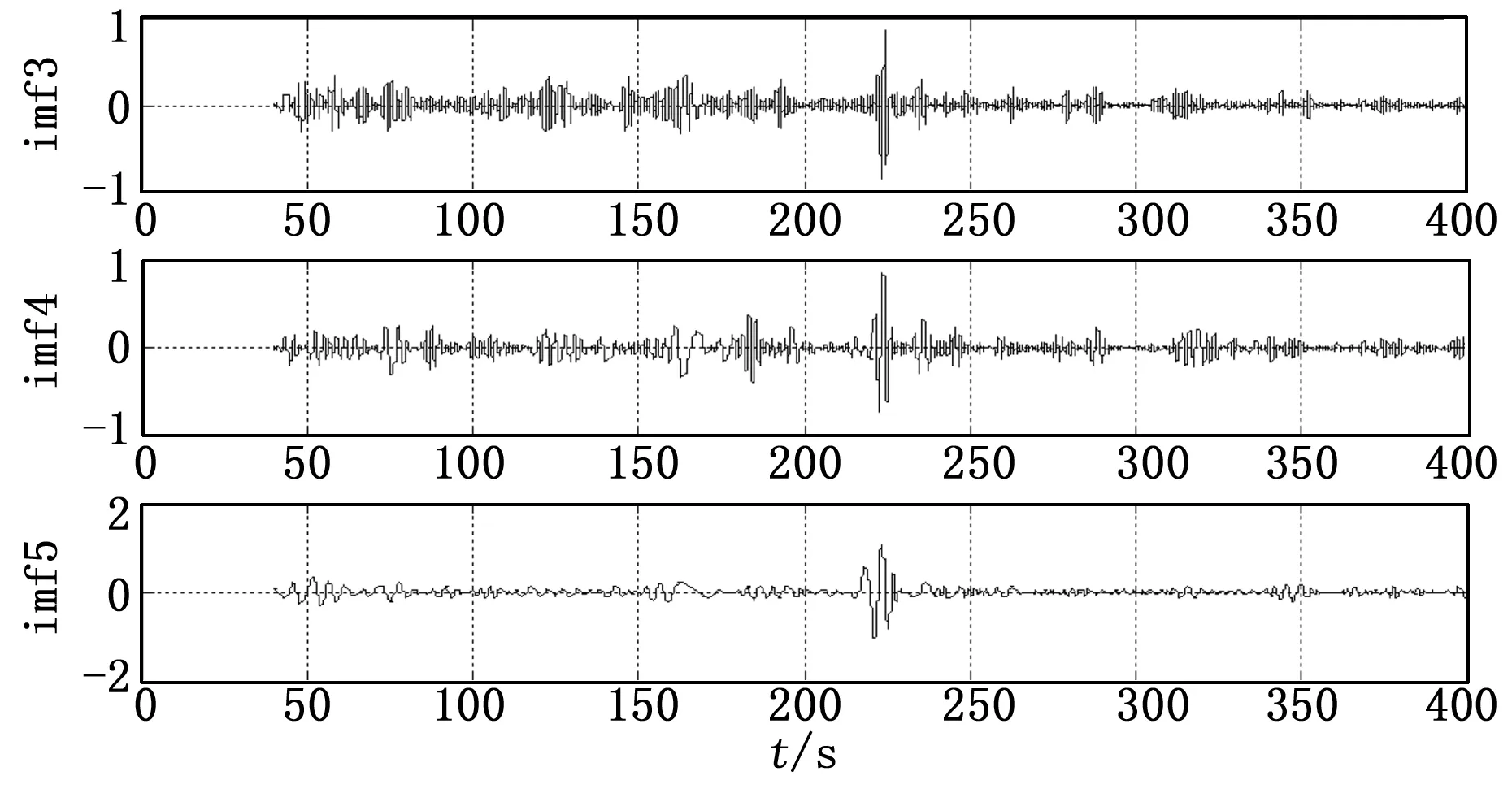
图22 EMD分解结果

以上几组实验，在不同强度漏气故障下，利用EMD对阀位响应信号进行分解，有效的检测出了阀位异常点即获得了漏气故障发生所对应的时刻,与我们的理论分析一致。实验采用工业生产中使用的正弦信号以及测试用的随机信号来模拟控制阀在线实际工况，结果表明EMD分解都可较准确的监测出故障。验证了EMD方法的自适应强的效果，即可较好的分析非稳态信号，为实际应用中控制阀故障诊断提供了可靠的理论和实验依据, 为以后的工业应用打好了基础。

4.2 Hilbert变换故障诊断

4.2.1 正弦信号诊断

(1)故障类型：无(正常状态)

故障强度：0，如图23～24所示。

图23 正弦阀位输出信号

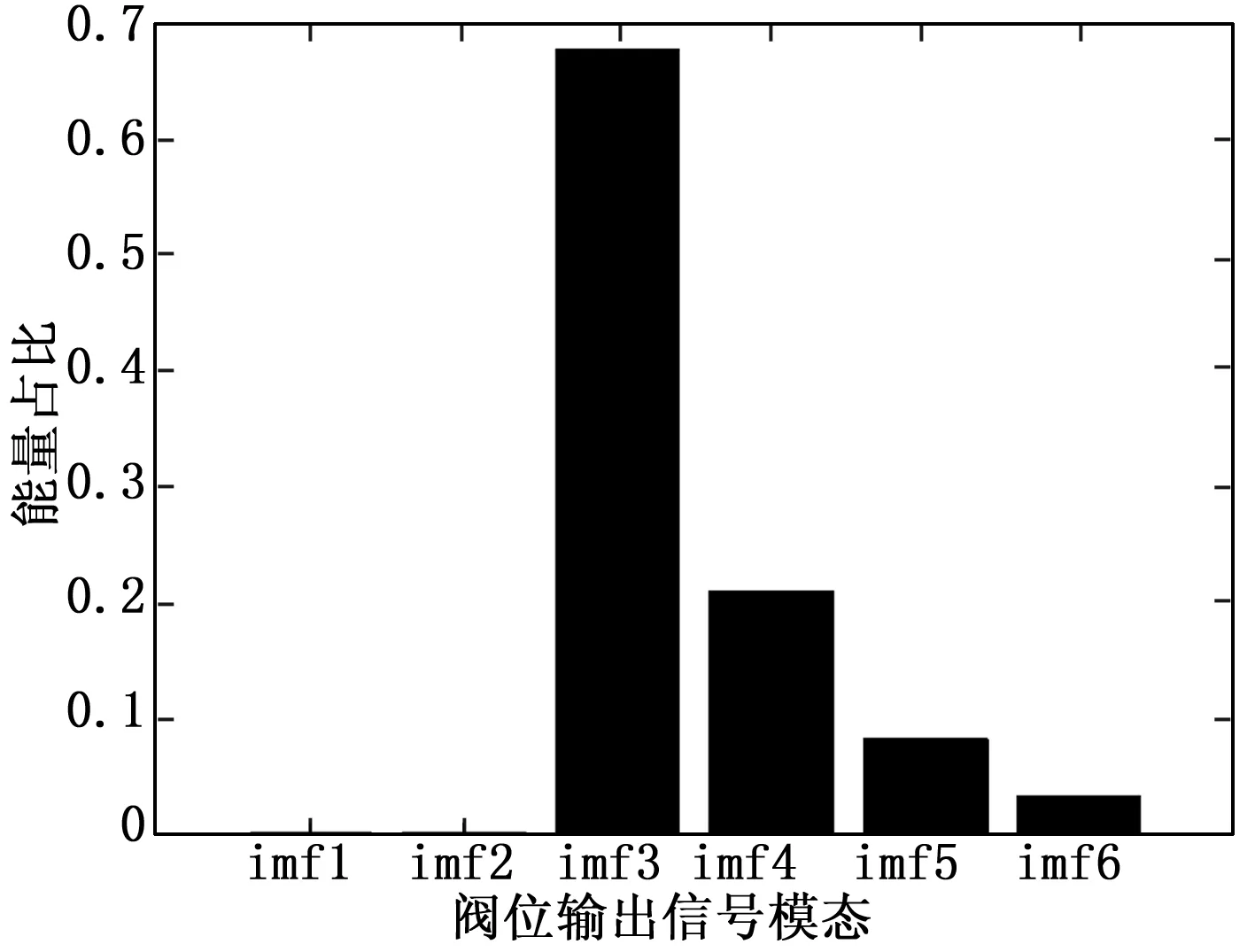
图24 正弦信号正常状态阀位模态

(2)故障类型：气室漏气

故障强度：小型手阀开度两圈(微弱)，如图25所示。

图25 气室漏气故障微弱状态阀位模态

(3)故障类型：气室漏气

故障强度：小型手阀开度四圈(较弱)，如图26所示。

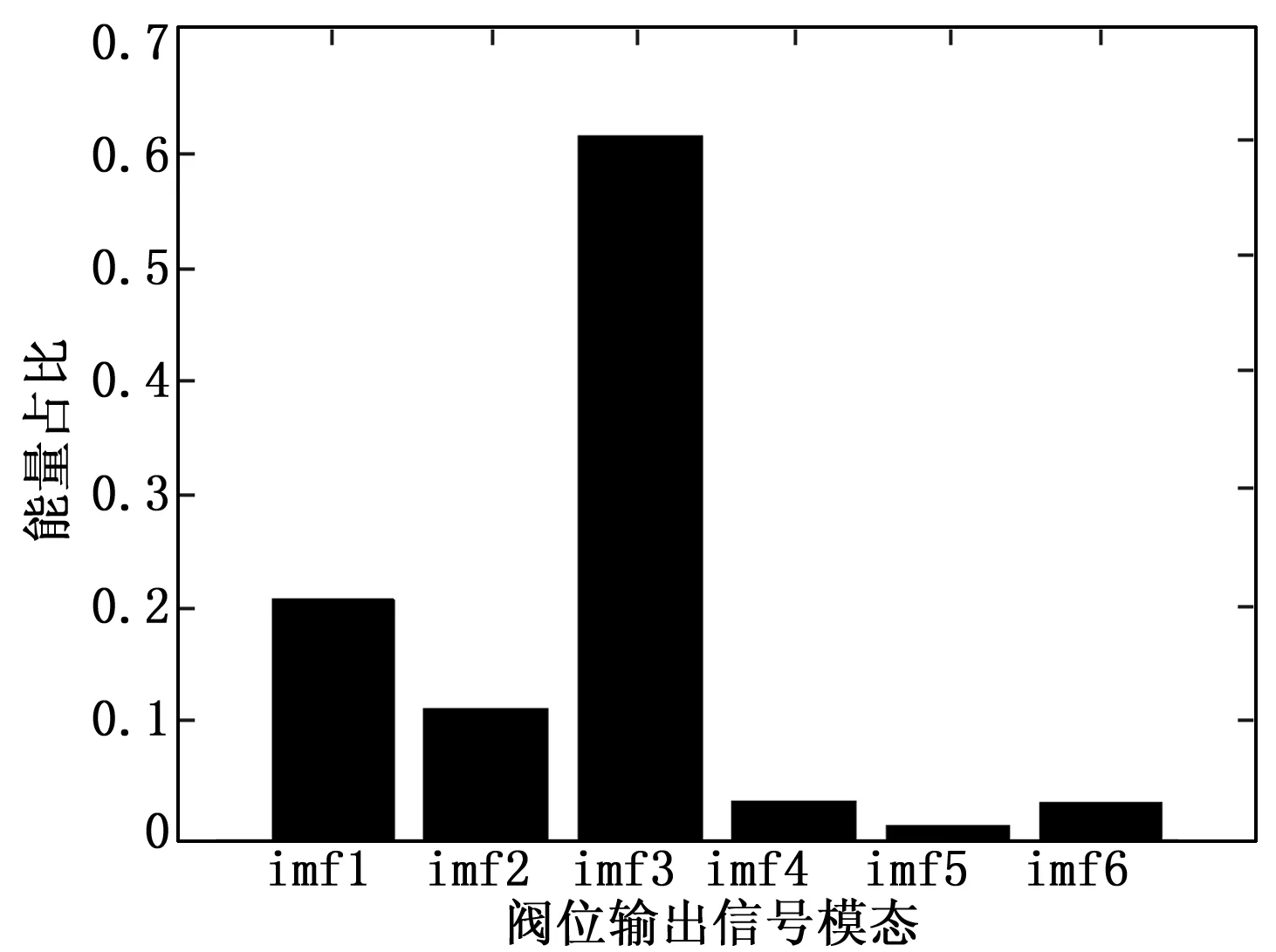
图26 气室漏气故障较弱状态阀位模态

此设定信号的气室漏气故障阀位模态一、二能量占比之和与故障强度的趋势图如图27所示。

图27 模态一、二能量和占比与故障强度的趋势图

4.2.2 随机信号诊断

(1)故障类型：无(正常状态)

故障强度：0，如图28～29所示。

图28 随机信号

图29 随机信号正常状态阀位模态

(2)故障类型：气室漏气

故障强度：小型手阀开度两圈(微弱)，如图30所示。

图30 气室漏气故障弱状态阀位模态

(3)故障类型：气室漏气

故障强度：小型手阀开度四圈(较弱)，如图31所示。

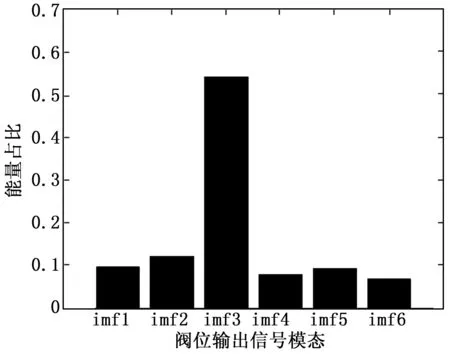
图31 气室漏气故障较弱状态阀位模态

此设定信号的气室漏气故障阀位模态一、二能量占比之和与故障强度的趋势图如图32所示。

图32 模态一、二能量和占比与故障强度的趋势图

4.3 实验结果分析

利用MATLAB/Simulink故障仿真模型的仿真分析和实验室气动薄膜单座直通阀的实验结果，可得出：

1)在气动控制阀正常运行状态下，利用HHT方法对阀位响应信号做EMD模态分解、Hilbert变换同时做出低阶模态能量占比图，据此可看出控制阀阀杆正常运作时阀位响应信号低阶模态的能量占比较小，而当控制阀出现漏气等气密性问题时，低阶模态特征频带信号的能量占比会随之增大。

2)研究主要针对的是控制阀气密性故障属于微弱强度的状态，属控制阀故障诊断分类的早期故障诊断方式。观察不同阀位设定信号模态低阶能量和占比与故障强度的趋势图，发现当气动控制阀气密性故障强度越大，即漏气越严重时低阶模态的能量占比和会变得越来越大。

3)仿真和实验结果复现验证了前文的理论分析；即：气动薄膜单座调节阀的气密性故障对于薄膜气室的造成的气压瞬间波动从而对阀杆造成巨大的振动冲击，最终引起控制阀阀位响应信号高频部分的振动加剧，低阶模态的特征频带信号能量便会相应的增多。

5 结论

本文基于希尔伯特黄变换进行了薄膜气动控制阀气密性故障的诊断研究，该方法通过对阀位相应信号进行分析，研究了各阶模态及其能量占比特性，使气动控制阀气密性故障诊断变得简洁易行，而且完整的实现了故障的在线的检测、诊断和强度识别。此方法的有效性通过模型仿真和实体阀实验得到了检验，可以把此方法推广到气动执行器其他故障的诊断上。