物理竞赛中含有非平衡电桥的复杂电路问题研究
姚春贤
(江苏省苏州市西安交通大学苏州附属中学,江苏 苏州 215000)
电路的分析联系着理论教学和实验两大物理主线,且其教学内容与实际有着密切的联系,在高中物理教学中有着举足轻重的地位.非平衡电桥在实际工程和科学实验中应用较广,如测量温度、压力、形变等[1-3],已成为中学物理竞赛、高考及高等学校物理实验的热点问题.为了更有效地指导学生学会灵活应用非平衡电桥法解决实际问题,培养其高层次的实验素养和创新实践能力,本文将对戴维南定理、基尔霍夫定律及△-Y变换法进行简单介绍,并将其应用于含有非平衡电桥的复杂电路问题中.通过实例演练和对比,总结出一套行之有效的求解方法,希望能够为广大师生提供一些参考.
1 戴维南定理
戴维南定理的推导和证明一般高中都不涉及(大学教材都会详细讲解[4]),为了便于学生理解,本论文将通过具体的实例给出戴维南定理的内容.在图1(a)电路中,E=10 V,r=1 Ω,R1=1 Ω,R2=2 Ω,R3=3 Ω,问R4上的电压为多少?对于这种只需计算复杂电路的一个支路上的电压或电流时,可以将这条支路画出,而把其他部分看作是一个由理想电源(E0)和内阻(R0)串联的电源来等效代替.E0为有源端口网络的开路电压,即将R4断开后A、B两端的电压,R0为去除端口网络中所有电源(将理想电压源短路,理想电流源开路)后的等效输入电阻,这就是戴维南定理.利用戴维南定理,如图1(a)所示的电路即可简化为图1(b)的形式,求等效电源的过程其实就是求等效电动势和等效内阻的过程,其中
(1)
(2)

(a)原始电路图
对于戴维南定理的使用条件及注意事项可参考文献[4].
2 基尔霍夫定律
基尔霍夫定律包括基尔霍夫电流定律和基尔霍夫电压定律.
基尔霍夫电流定律又称为基尔霍夫第一定律,简记为KCL,是电流的连续性在电路上的体现,其物理背景是电荷守恒定理.即在电路中任意一个节点上,任一时刻流入节点的电流之和等于流出该节点的电流之和,方程为
(3)
其中,n是与所求节点相连的支路数,ik是第k个进入或离开该节点的电流.
基尔霍夫电压定律又称为基尔霍夫第二定律,简记为KVL,是电场为位场时电位的单值性在电路上的体现,其物理背景是能量守恒定理.即沿着闭合回路所有元件两端的电势差(电压)的代数和等于0,方程为
(4)
其中,m是这个闭合回路的元件数目,uk是该回路中第k个元件两端的电压.
3 △-Y变换法
图2(a)和图2(b)分别为△网络和Y网络,△网络中的3个电阻分别为R12、R23和R31,Y网络中的3个电阻分别为R1、R2和R3,两个网络中任意两个节点之间的电压及分别从3个节点(节点1、节点2和节点3)流入的电流如图2所示,根据完全等效的原理,即
i1△=i1Y,i2△=i2Y,i3△=i3Y,
(5)
u12△=u12Y,u23△=u23Y,u31△=u31Y,
(6)

(a) 三角形联接电路图 (b) 星形联接电路图
可导出△-Y变换公式即
(7)
特别的,当构成△或Y电路的3个电阻相等时,

(8)
△-Y变换的推导和证明详细讲解见文献[4].对于△-Y变换的使用条件及注意事项可参考文献[5]的实例练习.
4 实例
计算如图3所示电路中经过电阻R9两端的电流I9.

图3 包含非平衡电桥的复杂电路
对于单一的非平衡桥式电路可直接通过戴维南定理、基尔霍夫定律或△-Y变换法进行求解,具体求解过程可参考文献[6].
仔细观察图3可知,该电路并非单一的非平衡电桥电路,而是包含了非平衡电桥的复杂电路(图3中右侧的虚线框内的部分为非平衡电桥),因此直接用戴维南定理、基尔霍夫定律或△-Y变换法进行求解比较困难,本文将戴维南定理与基尔霍夫定律或△-Y变换法相结合用于求解本题,其求解过程相对简单,且便于师生理解.
4.1 直接用戴维南定理求解
根据上文中讲述的戴维南定理及使用条件,首先对图3所示电路中的局部电路1进行一次戴维南等效,而其余部分保持不变,经等效变换后可得到如图4所示的电路.

图4 对局部电路进行戴维南等效后的电路图
其中,Req为局部电路1(图3所示电路中左侧虚线框内的电路)的等效电阻,Eeq为等效电压源.
经简化后,发现要求出流经电阻R9两端的电流,其电路结构仍然比较复杂,需对电路进行第二次戴维南等效,分别画出求解开路电压和等效电阻的电路图,如图5和图6所示.

图5 求解开路电压的等效电路图
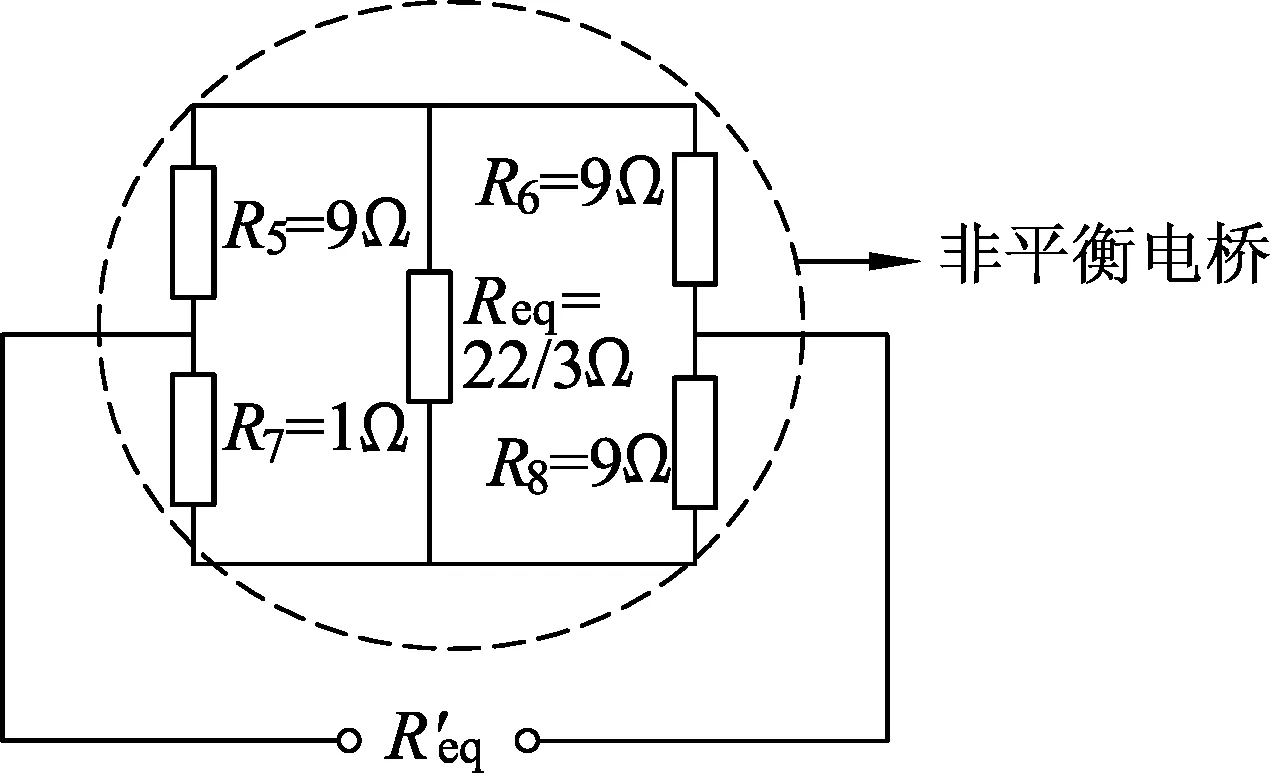
图6 求解等效电阻的等效电路图
仔细观察图5和图6,可知根据电路图5不难求出开路电压,但是在图6中仍然包含非平衡桥式电路(图6虚线框内的结构),因此仍然需要利用前文中讲述的△-Y变换法求解其等效电阻.
通过上述讨论可知,在此题的求解中,如果单独使用戴维南定理对其进行分析,其求解过程比较复杂而且计算量较大,本论文不做详细计算,读者可进行相关计算.
4.2 戴维南定理和△-Y变换法相结合进行求解
首先对图3所示电路中的局部电路1进行戴维南等效,而其余部分保持不变可得到如图7所示的电路.

图7 对局部电路1进行戴维南等效后的电路图
仔细观察该电路图,发现其中的非平衡电桥电路中包含了由对称电阻构成的三角形电路(图7中虚线框内的电路结构),因此可直接对虚线框内的电路结构进行△-Y变换,变换后可得如图8所示的电路结构图.
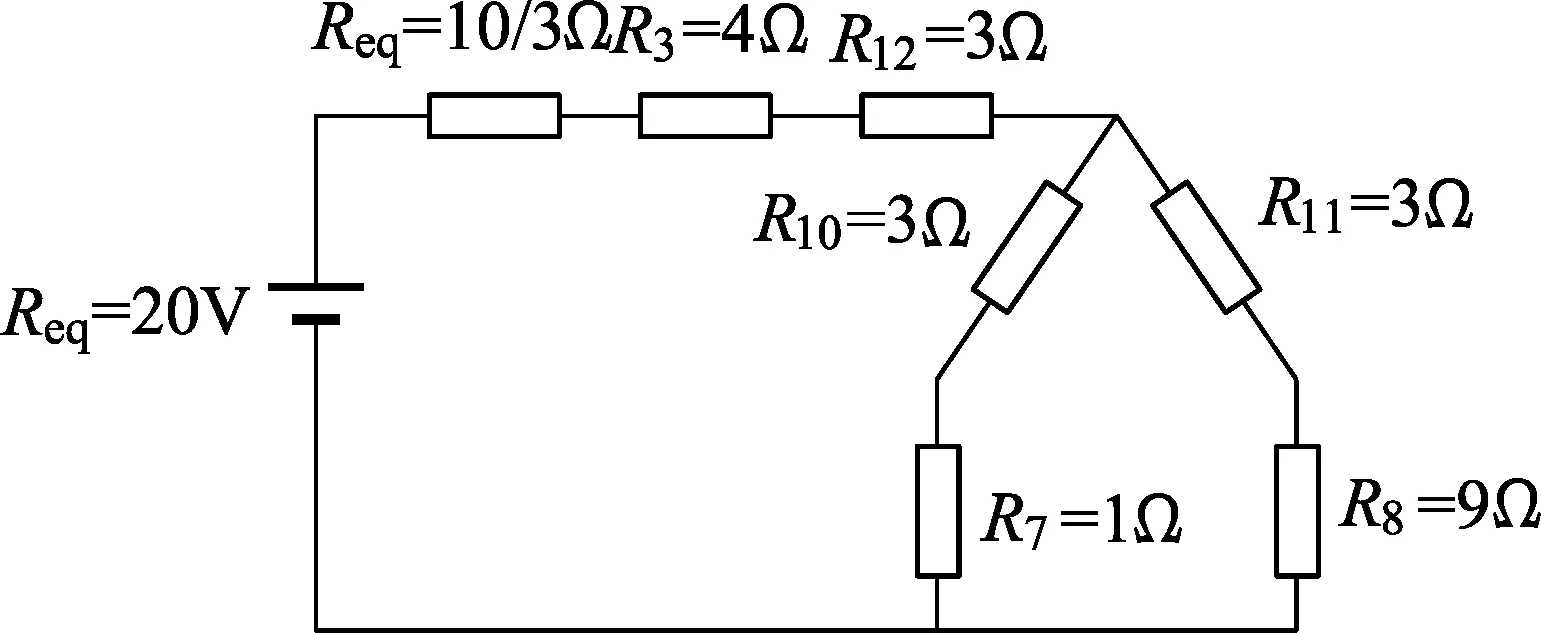
图8 经△-Y变换后的等效电路图
继续对图8进行串/并联等效可得如图9所示的等效电路.

图9 经串/并联等效后的电路图
图9中Ra,Rb和Rc分别为3个分支的等效电阻,Ia,Ib和Ic为流经电阻Ra,Rb和Rc的电流,其电流方向如图9所示.根据图9电路结构,很容易求解出电流Ib和Ic,其计算结果过程和计算结果如下.
(9)
(10)
(11)
将图9中所标识的数据代入方程 (9)~(11),可得Ia=1.5 A,Ib=1.125 A,Ic=0.375 A.根据图3可知,I9=Ib-Ic=0.75 A.通过比较4.1和4.2中的两种解法,可知戴维南定理和△-Y变换法相结合的方法对于求解含有非平衡电桥的复杂电路更加简便和容易.
4.3 戴维南定理和基尔霍夫定律相结合进行求解
这种解法的第1步跟4.2节中的解法一致,通过对电路中的局部电路1进行戴维南等效,而其余部分保持不变可得到如图10所示的电路.
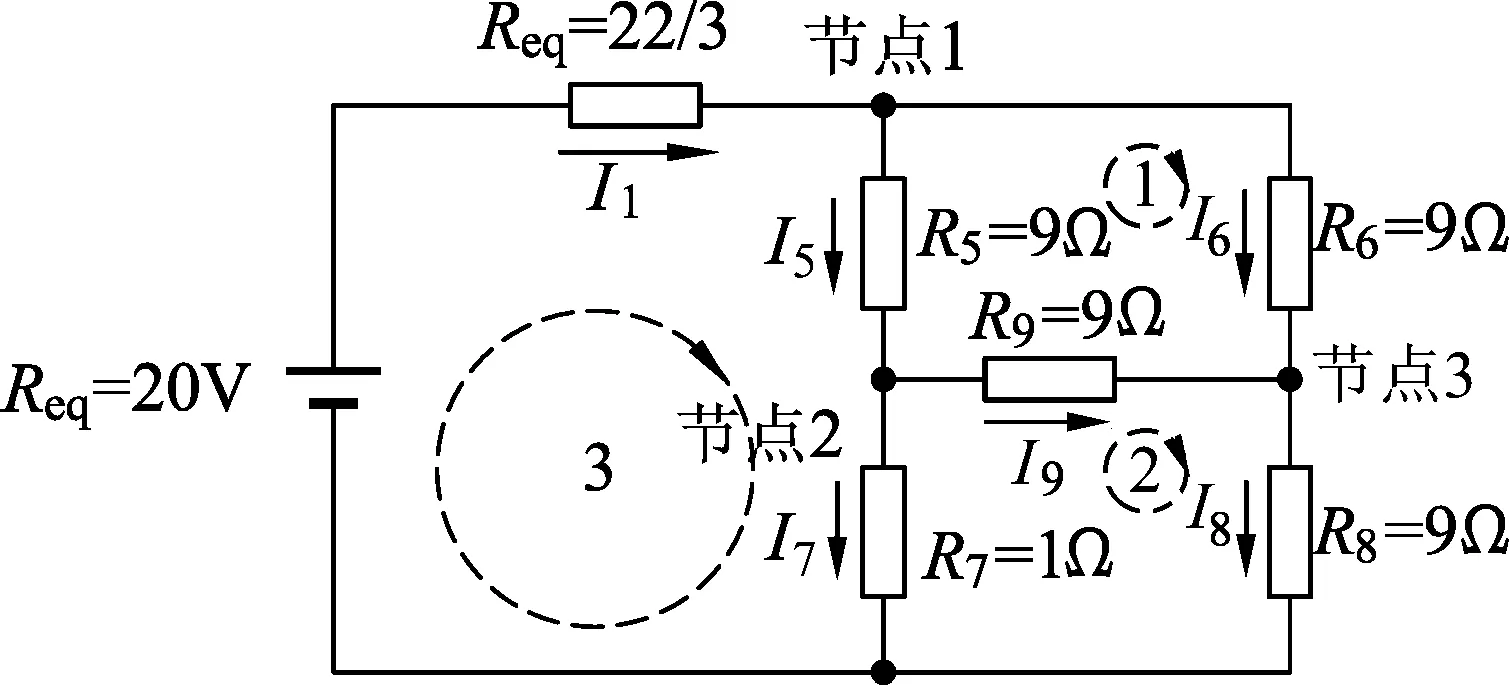
图10 对局部电路1进行戴维南等效后的电路图
然后利用基尔霍夫电流定律和基尔霍夫电压定律对该电路进行分析,在图10所示的电路中I1、I5、I6、I7、I8和I9分别为流过电阻Req、R5、R6、R7、R8和R9上的电流,其电流方向如图10所示.
选取如图10所示的节点1、节点2和节点3,并利用基尔霍夫电流定律分别对节点1、节点2和节点3列KCL方程,其方程组1的表达式如下.
节点1:I1-I5-I6=0.
(12)
节点2:I5-I7-I9=0.
(13)
节点3:I6+I9-I8=0.
(14)
选取如图10所示的回路1、回路2和回路3(3个回路的方向均为顺时针方向,如图10所示),并利用基尔霍夫电压定律分别对回路1、回路2和回路3列KVL方程,其方程组2的表达式如下.
回路1:I6R6+I9R9-I5R5=0.
(15)
回路2:I9R9+I8R8-I7R7=0.
(16)
回路3:I1Req+I5R5+I7R7-Eeq=0.
(17)
将题目中所有已知数据代入方程组1和方程组2,并联立方程组求解,可得,I9=0.75 A.
通过比较4.1、4.2和4.3中的3种解法,可知将戴维南定理与基尔霍夫定律或△-Y变换法相结合用于求解本题,其求解过程相对简单,且便于师生理解.
5 结论
非平衡电桥是电路理论教学环节中比较重要的一个环节,针对高中物理教学内容的特点和中学生的认知能力,本论文首先给出了戴维南定理、基尔霍夫定律和△-Y变换法的具体内容,并以实例的形式将戴维南定理与基尔霍夫定律或△-Y变换法相结合用于求解含有非平衡电桥的复杂电路,通过分析对比,让学生熟练掌握和应用戴维南定理、基尔霍夫定律和△-Y变换法在复杂电路中的应用,并得出了适宜中学生学习和掌握的求解方法.近两年来,在本校的教学实践表明,本方法得到了广大师生的一致好评.

