大坝安全监测中自动化比测方法的应用研究

唐宏华

湖南五凌电力科技有限公司，湖南怀化 419635

在信息技术快速发展带动下，大坝安全实时监测已经能够实现自动化，但由于受到设备、工艺和大坝所处环境等因素的影响，使自动化系统难免出现失真。所以，找到一种能对自动化系统所得监测结果进行自动校核，并确定精度与可靠性的方法至关重要。

1 数据比测基本概念与现状分析

对于大坝安全监测，其数据比测是指对由自动化系统得出的测量结果和由人工观测得出的结果进行比对与分析，用于验证所设自动化系统是否稳定与可靠。人工观测因历史较为久远，有着十分广泛的应用，且过程简单，所以是公认的有很高稳定性及可信度的方法；而自动化系统虽然也有很高的测量与频率，但可靠性与稳定性均需验证。因此，国家标准提出了需要对这两个结果实施对比的基本要求[1]。

就目前来看，行业中对大坝安全数据进行比测的具体方法与相关分析手段还没有明确的规定，在实际应用过程中，采用人工进行操作和阈值法相对普遍，另外，借助数据处理软件进行过程线的绘制，并用人工对曲线的走势及周期进行对比，也十分常见。但以上方法在很多方面都存在缺陷，比如：没有对测次对齐予以充分考虑，对比测的结果造成一定影响，这主要是因为没有保持对齐的序列会使对监测量信号进行判断时产生很大的偏差，而且采用人工将数据对齐，既烦琐，又容易出错，也会出现偏差；只采用不超过两种较为直观且浅层的对比方式，在分析能力上还较为欠缺。在实际应用过程中，一般以阈值法为主，对段时序小样本进行数据比测；数据挖掘有待提升，所得结果的说服力不足；必须采用人工进行操作，费时费力，而且计算能力不强，无法对长时序大样本进行数据比测。

2 比测方法基本原理与应用

2.1 方法原理

比测流程如图1所示。

图1 比测流程

2.1.1 以时序为基础的测次对齐

对大坝而言，在不同时间有不同的实际工作形态，尤其是关键部位，变化频率更高。为有效保证数据比测结果的合理性，两种测量方式的时序必须保持一致，所以在形成序列后，必须开展测次对齐。其方法为：将自动化系统所得测量数据对应的时间值作为基准，基于有效时间要求，找到和自身时间值最相近的观测结果；若未找到，则将这一自动化系统的实测结果丢弃，从而形成数量完全相等且时序保持一致的最佳样本组[2]。

2.1.2 超限分析

以预设变化阈值为依据，对每批相同测次两个结果差值进行判断，确认是否处在阈值范围内，此时将超限数量与所占百分比输出。

2.1.3 方差分析

这一步骤将超限的测值总数和所占百分比输出。

2.1.4 相关性与差异性

相同监测量在相同时序中采用两系统的测值序列，若方差和均值都没有明显差异，同时序列高度相关，则认为尽管监测方式有所不同，但所得结果完全一致。将样本数量记作K，采用自动化系统所得观测序列记作M，其均值记作EM，标准差记作 ；人工观测序列记作N，其均值和标准差分别记作EN、 。

①对系列均值进行差异性检验，若M和N没有明显差异，则可建立零假设，即EM=EN，进而可得以下检验统计量：

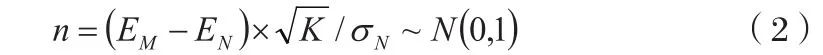
可见，n满足准正态分布，若将显著性水平设为a，可将拒绝域表示为 与，其中， 可通过查表获得，此时能输出不同显著性水平对应的接受结论及拒绝结论。

②对系列方差进行差异性检验，若M和N的方差没有明显差异，则可建立零假设，即 ，进而可得以下检验统计量：

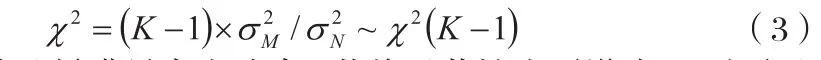
可见，统计量满足卡方分布，若将显著性水平设为a，则可通过查表获得拒绝域，此时能输出不同显著性水平对应的接受结论及拒绝结论。

③对系列相关性进行检验，即分析序列是否具有线性关系。当两者之间保持的线性关联较为紧密，则说明两者具有较高的趋同性及相似性，对于相关系数，可采用以下公式计算：

此时可将两个结果的线性相关系数输出。

2.1.5 判断规律性

所谓规律性的判断，是指以监测量发生的变化为一个随机的过程，然后把序列数值看作离散的信号量，以此为基础，进行傅立叶变换，对不同信号对应的特征量进行输出，同时予以对比。

2.2 方法应用

以某混凝土大坝为例进行分析，该大坝采用双向电容式自动化测量仪器，如图2所示，将测量周期确定为：在非汛期时，每天测量一次；在汛期，每8h测量一次。在人工观测方面，以视准测量为主，每7d测量一次。利用上述比测方法，时间间隔取8h，将测序对齐之后，可获得共884个结果，其比测结果为：以设计指标为依据开展超限分析与方差分析，超限测次数量为6，约占1.3%。从巡检日志中可以看出，其产生原因主要为自动化装置部分段所用防冻液大量挥发，使浮力降低或直接被冻住，导致测量结果失准；相关系数经计算等于0.97，说明两者为正相关；采用人工观测所得序列，其均值和标准差分别为0.10mm、1.1；采用自动化系统观察所得序列，其均值和标准差分别为0.097mm、1.17，两者均值对应的差异统计量结果为0.057，当置信度为95%时，不拒绝原定假设，两者方差对应的差异统计量结果为500.04，当置信度为95%时，同样不拒绝原定假设。通过上述分析可以看出，该大坝所用两种测量方式，无论在均值和标准差，还是相关性上，均具有良好性能，满足相关标准要求[3]。

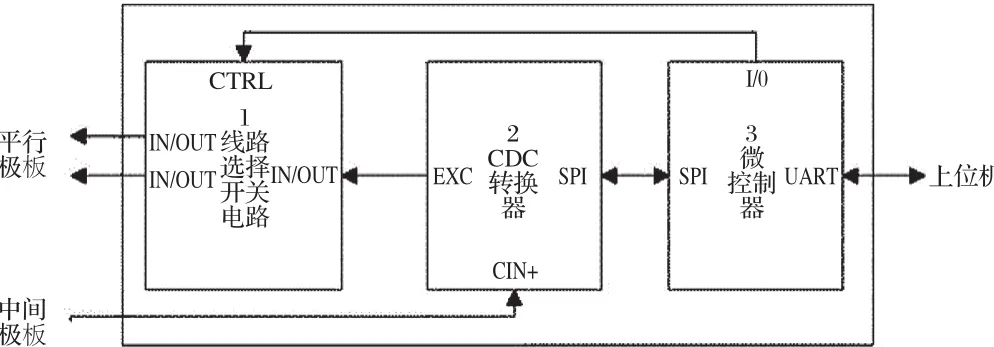
图2 双向电容式自动化测量仪器

3 结语

因数据比测对自动化观察结果验收及校核均有重要作用，所以在当前引起了很多人的重视。目前行业中最常见的方式就是人工，选取一段时间内适量样本开展差值对比，虽然方法简单，但具体操作和执行十分烦琐，所得结果的说服力及可信度均亟待提升。

对此，本文基于数据预处理，提出一种多维度比测方式，通过研究和应用，可将其优势特征总结如下：

首先，利用自动化比测，能打破数据规模带来的限制，使比测结果准确性得以大幅提高；

其次，比测开始前，先进行测次对齐，这样可以在保证样本质量的同时，提高可信度；

再次，在包含方差、差异性、相关性及与规律性等在内的多个方面对两种数据结果的关联性进行深度挖掘，所得结果更加全面，同时还具有校核的功能；

最后，算法十分清晰，具有良好的鲁棒性，容易实现，能满足现在越来越多长时序大样本对数据比测提出的要求。

以此，该方法可以十分充分地整合现有测量数据，且更为深入与全面地对相同监测量在采用不同方法后所得结果的差异性及关联性进行分析，进而为大坝自动化系统持续优化提供依据。