基于约束差异最大化投影算法的表情识别
王 超,潘正高,路红梅,李雪竹
宿州学院信息工程学院, 宿州,234000
在人的情绪判别和人际交往中,人脸表情识别起到了重要作用[1,2],因此人脸表情识别在国内外引起广泛关注。目前多种模式识别的方法被应用到人脸表情自动识别中。主分量分析(PCA)[3]算法将人脸数字图片转换成一个矢量,大量样本集组成一个矢量集,对这些矢量集的协方差矩阵求特征值特征向量。主要特征值对应的特征向量映射下的人脸图片作为特征人脸进行分类。线性判别分析(LDA)[4]算法充分利用类别信息构造一个类间散度矩阵和一个类内散度矩阵并且通过寻找一组投影向量使得这两个散度矩阵的迹之比最大。这组投影向量作用于每一个样本使得投影后的人脸样本称为fisher脸,并使用这个fisher脸来进行分类。此外线性特征提取方法还有独立分量分析(ICA)[5]。以上算法是对人脸表情图片整体直接做特征提取方法然后给分类器分类。
还有一些算法是对图像求局部特征和整体特征融合的方法。文献[6]人脸表情识别通过两个阶段的特征提取,第一阶段通过限制的局部二值模式(LBP)将人脸图片转变成特征图片,第二阶段对这些特征图片利用基于块的中心对称局部二值模式提取具有鉴别信息的特征,然后利用支持向量机(SVM)分类。文献[7]融合了PCA和嘴巴部分的LBP特征进行人脸表情识别,利用SVM进行分类,在作者自己构造的样本数据上取得了比传统特征提取效果更好的分类结果。文献[8]利用了简化的局部梯度编码算法,仅仅采用了水平方向和垂直方向的分量进行编码,在日本女子人脸表情数据集(JAFFE)上测试这个算法,比传统的LBP和gabor特征具有更好分类效果而且运行时间上更快。针对PCA和LBP融合算法对随机噪声和光照变化容易受影响的特点,文献[9]提出了融合PCA整体特征和局部方向模式(LDP)特征,LDP算子作用于眼部和嘴部提取其局部纹理特征,实验证明这种融合算法比单独使用PCA提取特征或者PCA和LBP融合算法有更好的效果。
流形学习算法是非线性特征提取方法,文献[10]提出一种流形学习的方法进行人脸表情分类。它基于这样一个假设,不同的表情分布在不同的流形上(维数也未必相同),提出一个人脸表情建模和分类的整体框架。每种表情的本征特征单独学习,通过遗传算法(GA)从分类角度获取每个表情流形最佳维数。分类标准也是新定义的,在表情流形上最小的重建误差作为分类的判别标准。文献[11]提出使用改进的LBP和类规则的局部保持投影(LPP),LBP强调了人脸在特定基准点的部分信息,另外也增强了面部特征和表情类别的联系。LPP通过降维使得不同类独立性最大化,另外也保持了局部特征的相似性。文献[12]提出了一种有偏的子空间学习算法来鲁棒处理非对齐人脸表情图片,同时提出有偏线性判别分析(BLDA),该算法对于差别很小的类间样本给予很大的惩罚,对于差别很大的类间样本给予很小的惩罚,这样可有效提取鉴别特征。算法为了更好地利用测地信息,设计了一种加权有偏差异fisher分析(WBMFA)算法,利用图嵌入准则提取鉴别信息,该算法适用于数据集不满足高斯分布的情况。约束差异最大化投影[13](CMVM)算法由2008年李波等提出,应用于人脸识别等领域。该算法在构造差异化判决式上利用类别信息,而且在构造近邻关系判决式上利用了近邻信息。该算法主要目标是保持同类的人脸表情样本投影后更紧凑,不同类人脸表情样本投影后更加离散。本文采用此算法在人脸表情识别领域,是首次尝试。
1 约束差异最大化投影算法
CMVM算法的思想来源于差异最大化展开(maxmum variance unfolding MVU)的流形学习算法[14,15]。该算法假设近邻的样本之间由刚性杆连接,算法的目标是最大化两样本之间距离同时又不破坏近邻样本之间的刚性连接。CMVM算法从数据降维角度考虑,把原始输入高维数据通过投影映射到低维空间。这个过程中保持了近邻样本之间的刚性连接,同时又最大化两两样本之间的距离。
1.1 邻域的选择
首先是近邻样本选择,近邻样本之间的距离用欧式距离来度量。有两种判断近邻的方法,一种是(K-Nearest Neighbor,KNN)就是在欧式距离度量的样本之间寻找距离最小的前K个样本。另一种方法叫ε-ball的方法,该方法以中心样本为圆心,以一定长度ε为半径画超球。超球范围内的样本,统称为中心样本的近邻样本。表达近邻关系样本关系矩阵的元素定义如下:
(1)
(2)
1.2 近邻关系判决式
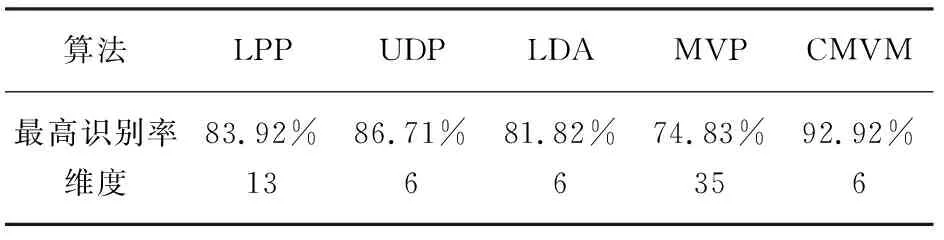
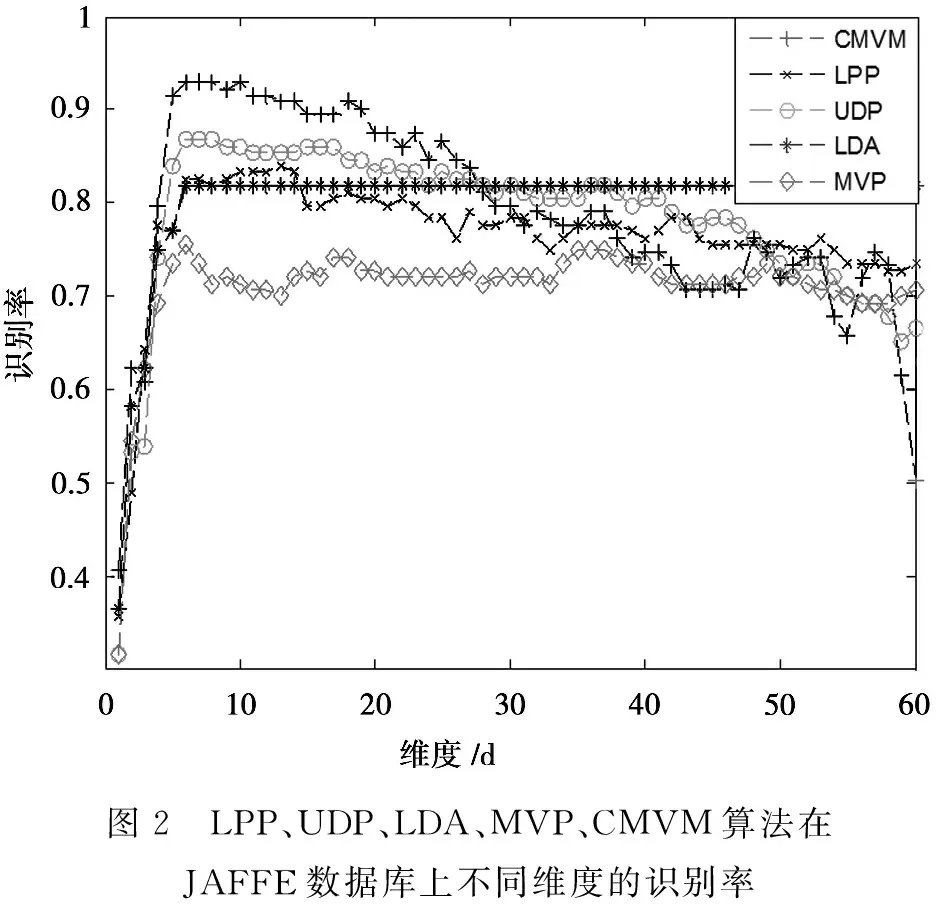
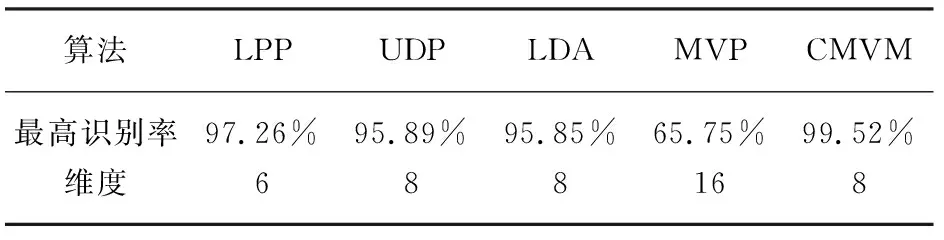
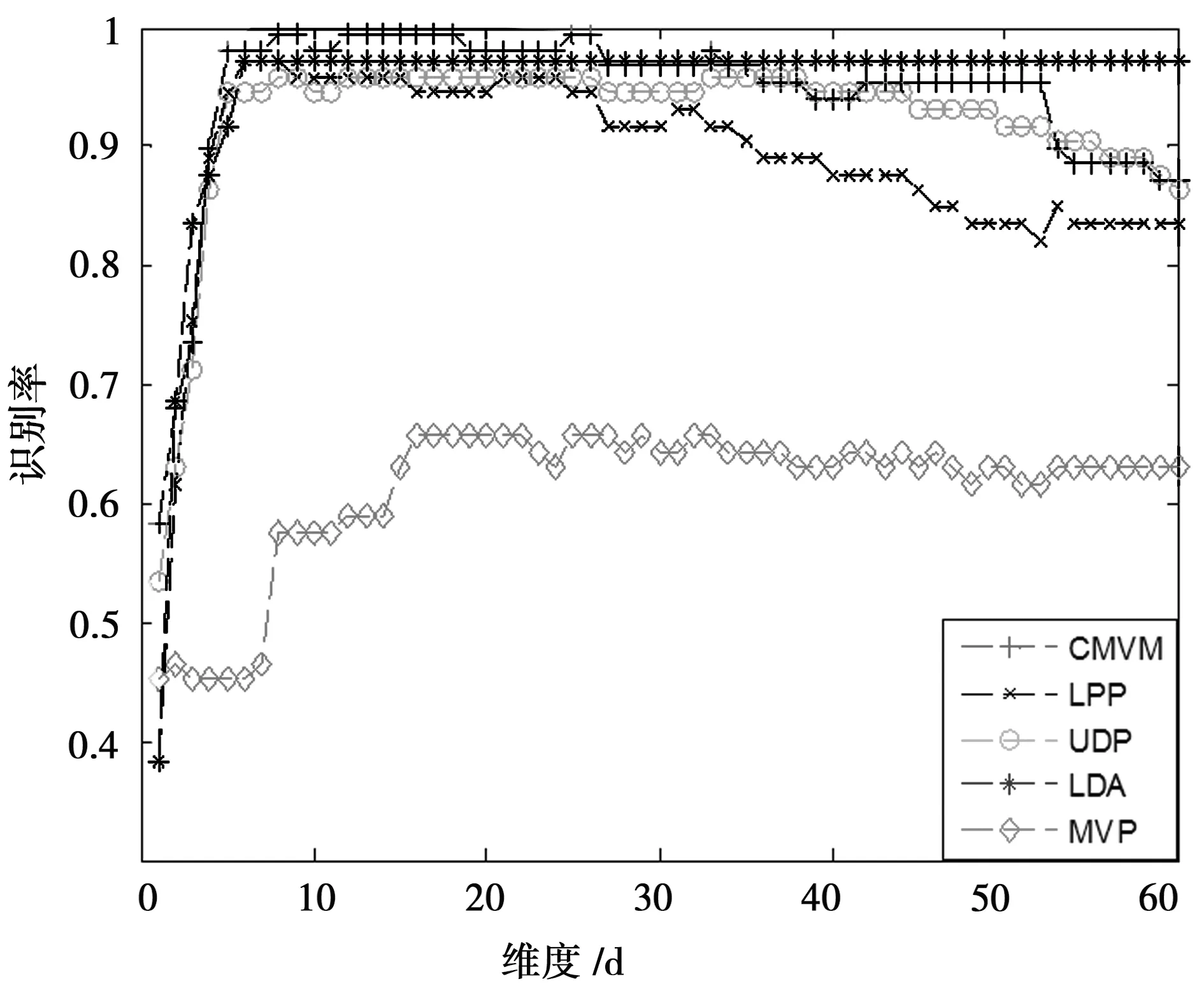
CMVM算法目的是寻找一个投影矩阵W,使得投影后的样本维数更低同时更有利于分类。输入样本xi∈RN是N维空间中的样本矢量。投影后的样本yi∈RM是M维空间中的样本矢量。其中yi通过这样一个投影关系式得到yi=WTxi,且满足M =2tr{Y(P-L)YT} (3) CMVM算法假定同类样本都嵌入在同一个流形上,不同类样本嵌入在不同的流形上。欧式距离大小经常来定义样本间差异大小。此处用欧式距离平方来定义不同类的样本所在流形的差异,使其在欧式距离度量下最大化展开。首先构造一个类别关系矩阵C定义如下: (4) 差异化判决式定义如下: (5) 由线性映射关系可以得到JL、JD关系式如下: (6) (7) 根据算法思想,即使不同类样本在不同流形上嵌入差异最大,同时保持所有流形近邻结构不变。可以得到以下的最优化关系式。 如引言所述,把整幅图像看作一个整体,例如一幅m×n的数字图像可以看作是一个m×n维空间中的一个点。如何将这个高维空间中的点有效维数提取出来,将无关的冗余特征除去,将是特征提取算法要完成的任务。这里使用的特征提取算法有CMVM、LPP、UDP、LDA、MVP等。这些算法将作用在JAFFE日本女人表情人脸数据库和CK+人脸表情数据库上。将这些算法作用在这两个数据库上之前,使用了PCA算法来降维,以避免小样本问题。降维后的数据使用KNN分类器来进行分类预测类别。 JAFFE(The Japanses Female Facial Expression)数据库即日本女性面部表情数据库,该数据库共有213张表情图片,由10个女性的7种表情图片组成(见图1)。每种表情图片2-3张照片。算法表示总的识别率如表1所示。总共有213张图片,前150张作为训练数据,后163张作为测试数据,构成一组数据。这组数据样本间的差异,不仅有不同表情之间的差异,而且相同的表情样本之间还有不同个体之间的差异,相对来说识别难度较大。 表1 LPP 、UDP、LDA、MVP、CMVM算法在JAFFE数据库上总最高识别率对比 图1 JAFFE数据库七种表情图片 由表1可知,最高识别率CMVM高出UDP接近6个百分点,高出LPP接近9个百分点,高出LDA接近11个百分点,高出MVP接近18个百分点。而且CMVM算法达到最大识别率的维数很小比起LPP和MVP算法。所以本文中使用的CMVM算法在表情识别上有效。 将5种算法在JAFFE数据集的测试集上不同维度的识别率用图2展示出来。分析图2可知,CMVM算法总体识别率最高达到92.92%,而且识别率比较稳定,在维度为6和7上都达到了92.92%的识别率。其他维度上的识别率也普遍高于LPP算法和UDP算法。UDP算法的识别率在一些维度上取得了和CMVM算法同样的识别率,但是到了28维后,流形学习算法LPP,UDP,MVP包括本文算法CMVM下降比较快。高维度时识别率下降是值得探讨的一个问题。 该数据库是在 Cohn-Kanade Dataset 的基础上扩展来的。该数据库比起JAFFE 要大得多。包含表情的标签和动作单元的标签。 该数据库包括123个人,593 个图像序列,每个图像序列的最后一张图片都有动作单元的标签,而在这593个图像序列中,有327个图像序列有表情的标签。每个序列图片都是从中性表情到这个表情标签的表情一个序列(图3所示为CK+数据库一个实验者的七种表情)。因此如何合理区别中性表情到这个表情标签是一个问题。也是影响分类准确度一个关键点之一。 图2 LPP、UDP、LDA、MVP、CMVM算法在JAFFE数据库上不同维度的识别率 每个表情选取7张图片作为测试,其余5张作为测试样本,使用表中列举的5种算法分别进行训练和测试得到识别率见表2。 图3 CK+数据库七种表情图 算法LPPUDPLDAMVPCMVM最高识别率97.26%95.89%95.85%65.75%99.52%维度688168 图4 LPP、UDP、LDA、MVP、CMVM算法在CK+数据库上不同维度的识别率 分析表2可知最高识别率仍然是CMVM算法达到99.52%,其次分别是LPP最高识别率为97.26%,UDP最高识别率为95.89%,LDA识别率为95.85%,但是MVP识别偏低为65.75%。LPP在第6维就达到了最高识别率,CMVM、UDP、LDA这三种算法均在第8维达到了最高识别率。但是MVP却在第16维才达到最高识别率。将本文所用到的5种算法在不同维度上的测试准确率展示如图4。由图4分析可知CMVM在11个维度上都达到了99.52%的识别率,而且下降不明显。LDA算法比较稳健,达到最大值95.85%后则保持该识别率,且识别率不随着维度上升而下降。LPP算法虽然最大识别率为97.26%,但无CMVM算法稳定,随着维度增加迅速下降。UDP算法的表现介于LPP和LDA算法中间。MVP算法表现最差,实验表明MVP算法不适合表情识别。 本文提出使用约束差异最大化投影这一流形学习算法来进行人脸表情数据降维分析,通过在JAFFE和CK+这两个数据库上实验,验证了流形学习算法的有效性。进一步的工作是推广这个算法在实时动态的表情识别上的应用,争取在实时识别上可以达到每秒30帧的处理速度,识别效果可以达到98%以上。另外,差异最大化投影算法在表情识别数据集上表现较差差的原因还有待进一步研究。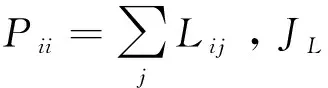
1.3 差异化判决式构造
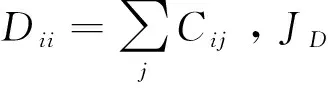
1.4 关系式改写
1.5 最优化目标式
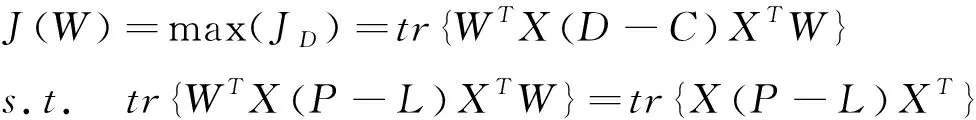
2 实 验
2.1 JAFFE数据库上实验

2.2 CK+数据库上实验

3 结 论

