恒高温下钢管混凝土的界面黏结应力-滑移关系模型研究*
薛媛媛, 陈 俊, 谭清华
(1.湘潭大学 土木工程与力学学院,湖南 湘潭 411105;2.国防科学技术大学 土木工程系,湖南 长沙 410072)
钢管与混凝土之间可靠的黏结是两种不同性质的材料能共同工作并较好发挥出各自优点的前提[1].目前国内外对常温下和高温后钢管混凝土的平均黏结强度和黏结滑移关系模型研究相对较多.1975年Virdi和Dowling[2]对常温下钢管混凝土的界面黏结性能进行了探索,接着Roeder、Aly、Radhika、Tao等[3-6]也开展了试验研究.国内薛立红、刘永健、陶忠等[7-10]也开展了常温下的相关试验研究.以上试验研究主要采用推出试验方法,研究的参数包括混凝土强度、混凝土的收缩、养护条件、龄期、矿物添加剂及添加量、试件宏观偏差、钢管内表面粗糙程度、径厚比、长径比、偏心率、钢材和混凝土材料类型等.试验结果表明各参数对钢管混凝土界面黏结强度均有一定的影响,但由于试验条件的差异,得出的结论不完全一致.对火灾后钢管与混凝土的界面性能,陈现、张春亮、Tao、David等[11-14]采用推出滑移试验方法开展了相关研究,研究的参数主要包括火灾作用时间、长径比、截面形状、混凝土强度、养护条件及混凝土类型等.结果表明,火灾作用将使界面黏结强度降低.
以上研究大多侧重于界面黏结强度的研究,为合理建立钢管和混凝土界面的关系模型奠定了基础.目前,界面关系模型的建立主要有两种途径:(1) 基于理论的关系模型,即基于一定的简化和假设,从力学平衡的角度推导出界面关系模型.该类模型物理意义明确,但考虑的因素有限.如康希良、辛海亮等[15-16]从理论上推导出钢管与混凝土界面黏结滑移的关系模型.(2) 基于试验的关系模型,即在大量的试验数据基础上,通过数据拟合得到关系模型.该类模型在试验研究的范围内有较高精度,但外延性较差.如Jercome、刘永健、刘玉茜、许开成、林思奇、Tao等[9,13,17-20]通过大量试验数据拟合得到钢管和混凝土界面的黏结应力-滑移关系式.
综上所述,目前国内外学者已研究常温下和高温后钢管混凝土的界面平均黏结应力并提出黏结-滑移关系式,而高温下钢管混凝土的界面黏结滑移关系模型还未见相关报道.本文基于陈俊等[24]对恒高温下钢管混凝土界面黏结性能研究的试验结果并参考常温下试验结果,提出了高温下钢管混凝土界面的黏结应力-滑移关系曲线,得到恒高温下钢管混凝土界面黏结应力-滑移关系.
1 常温下界面黏结应力-滑移曲线
常温下钢管混凝土荷载-滑移曲线具有以下变化特征:在钢管与核心混凝土滑动之前,曲线基本呈线性关系,且缓慢发展;在钢管与核心混凝土滑动之后,曲线呈非线性变化,且迅速发展.当钢管混凝土界面胶结力和微观的机械咬合力高于界面的摩擦力时,一旦钢管和混凝土界面发生黏结破坏,曲线就出现了明显的峰值荷载点及其随后的下降段,如图1(a)所示;反之,当钢管混凝土界面胶结力和微观的机械咬合力比界面的摩擦力低时,曲线仅出现明显的非线性性质,产生拐点,无明显峰值,如图1(b)所示.荷载-滑移曲线在经过下降段或拐点后,由于钢管的“宏观偏差”使得如图1(a)和(b)所示的两类曲线后期发展也有三种趋势:当钢管内径沿长度方向保持基本不变时,曲线近似水平;当钢管上部内径大于下部内径时,曲线为上升趋势;反之则为下降趋势[7-8].

在试验结果的基础上,为简化分析,关系模型主要有以下两种形式:
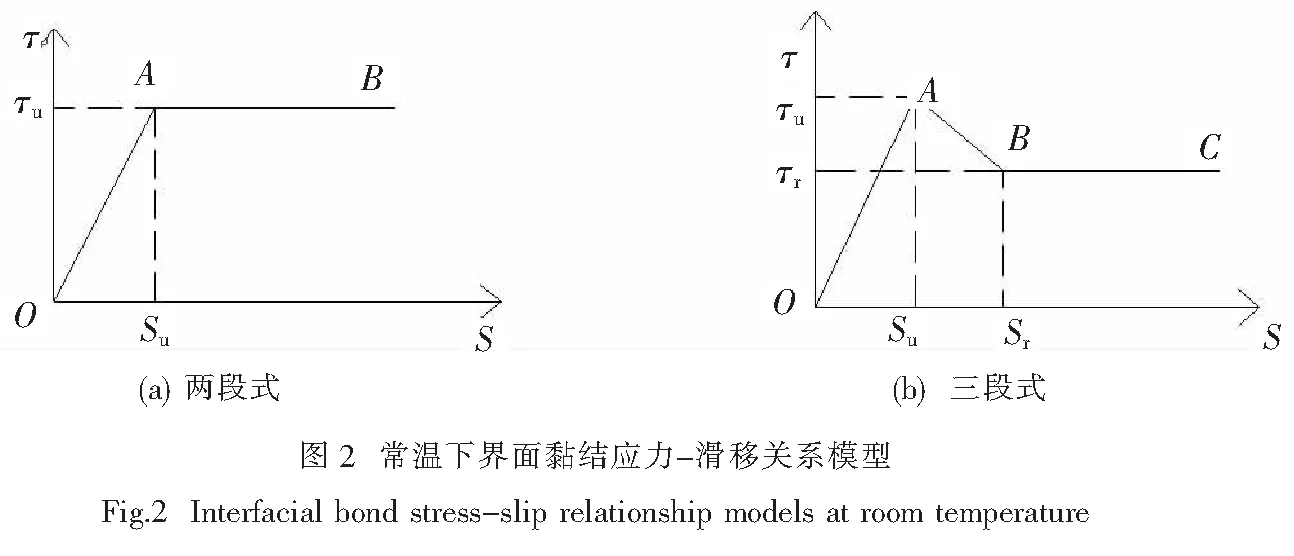
(1) 两段式.当黏结应力小于峰值荷载对应的平均黏结强度时,黏结应力近似与相对滑移呈线性关系;当黏结应力达到峰值荷载对应的平均黏结强度后曲线保持水平,如图2(a)所示.文献[9, 17]的曲线采用了类似图2(a)所示的简化模型.
(2) 三段式.当黏结应力小于峰值荷载对应的平均黏结强度时,黏结应力近似与相对滑移呈线性关系;当黏结应力达到峰值荷载对应的平均黏结强度后,相对滑移快速发展,曲线迅速下降;最后保持水平段,即为剩余黏结强度,如图2(b)所示.文献[2-8, 10, 18, 19]的曲线采用类似如图2(b)所示的简化模型.
2 恒高温下界面黏结应力-滑移关系
2.1 恒高温下界面黏结应力-滑移曲线
根据陈俊等[24]对恒高温下钢管混凝土界面黏结性能研究的试验结果,恒高温下的界面黏结应力-滑移的曲线与常温下规律类似,具体表现为:7根试件可归类于有明显峰值点的图1(a)中曲线①,7根试件可归类于有明显峰值点的图1(a)中曲线②,9根试件可归类于无明显峰值点的图1(b)中曲线④;由于钢管的“宏观偏差”使得曲线在峰值点或拐点后出现上升或下降的趋势,而钢管为理想平直状态时,曲线表现为水平.为简化分析,并参考常温下的相关结果,本文拟采用三段式模型建立恒高温下钢管混凝土界面黏结滑移关系模型,其表达式如式(1)所示.
(1)
式中:τT为高温下钢管混凝土界面黏结强度,单位为MPa;τr,T为高温下峰值点后的剩余黏结强度,单位为MPa;τu,T为高温下黏结滑移曲线峰值荷载对应的平均黏结强度,单位为MPa;sT为高温下钢管混凝土构件端部钢管与混凝土的相对滑移,单位为mm;su,T为高温下黏结滑移曲线平均黏结强度对应的滑移值,单位为mm;sr,T为高温下黏结滑移曲线峰值点后下降段末对应的滑移值,单位为mm.根据文献[24]推出的试验荷载滑移曲线可知,试件到达峰值点后下降段末对应的滑移值约为7 mm,则取sr,T=7 mm.
2.2 平均黏结强度和剩余黏结强度的回归
根据已有的试验研究与分析结果,可知影响常温下钢管混凝土界面平均黏结强度的主要因素有混凝土强度、钢管内表面粗糙度、试件长径比、径厚比等[2-10],同时结合文献[24]的试验与分析结果,可知影响恒高温下钢管混凝土界面平均黏结强度的因素主要有恒温温度、径厚比、长径比.因此,本文的回归分析中将主要考虑以上3个因素,混凝土强度作为主要的影响因素.
首先对文献[24]试验数据进行归一化处理,得到不同恒温温度下的界面平均黏结强度及对应的相对滑移与温度的关系,如图3和图4所示,拟合公式如式(2)和式(4)所示.对以往常温下试验数据[19,21-23]及陈俊等[24]常温下试件试验数据进行线性回归可得到常温下钢管混凝土界面平均黏结强度及对应的相对滑移与各主要影响因素的关系,如式(3)和式(5)所示.最后得出恒高温下钢管混凝土界面平均黏结强度及对应的相对滑移与各主要影响因素的关系.
(2)
τu,0=2.053+0.028fcu-0.222L/D-0.037D/t,
(3)
式中:γτ,T是恒高温下钢管混凝土界面平均黏结强度与相应常温下界面平均黏结强度比值,即平均黏结强度的火灾作用折减系数;τu,T是恒高温下黏结滑移曲线峰值荷载对应的界面平均黏结强度,单位为MPa;τu,0是常温下黏结滑移曲线峰值荷载对应的界面平均黏结强度,单位为MPa;T是钢管混凝土柱恒温温度,单位为℃;D/t为圆钢管的径厚比;L/D为圆形试件的有效长径比;fcu为混凝土的轴心抗压强度,单位为MPa.
(4)
su,0=1.481+0.028fcu-0.11L/D+0.007D/t,
(5)
式中:γs,T是恒高温下钢管混凝土平均黏结强度对应的相对滑移与相应常温下对应值的比值,即相对滑移的火灾作用折减系数;su,T是恒高温下平均黏结强度对应的滑移,单位为mm;su,0是常温下平均黏结强度对应的滑移,单位为mm.

提取文献[24]各试件峰值点或拐点后(即相对滑移值sr,T=7 mm)对应的剩余黏结强度τr,T的试验数据,回归得到τr,T如式(6)所示.
τr,T=1.116 49τu,T-0.070 1.
(6)
2.3 计算结果与试验结果的对比
根据式(2)和式(3)得到平均黏结强度计算值与文献[24]试验值对比,结果如图5所示.式(4)和式(5)得到平均黏结强度对应的相对滑移计算值与文献[24]试验值对比,结果如图6所示.
由图5和图6可知,试件平均黏结强度计算值与试验值比较接近,只有试件C10-2和C11-2偏离有点明显,可能是由于材料本身的离散性导致的,计算值与试验值比值的平均值为0.936,标准差σ为0.246;而试件平均黏结强度对应的相对滑移计算值与试验值偏差比较大,计算值与试验值比值的平均值为1.202,标准差σ为0.398.由于其个别试件计算值与试验值的偏差从而导致离散系数偏大.


根据前文提出的高温下界面黏结应力-滑移关系式(1)~(6),取文献[24]中试件的参数,拟合得出试件的黏结应力-相对滑移曲线,将其与试验黏结应力-相对滑移曲线对比,结果如图7所示(由于篇幅限制,本文仅列出了6根不同温度下的试件对比曲线).由图可知,总体上,本文提出的界面黏结应力-滑移曲线与相应试验曲线趋势比较吻合,平均黏结强度和对应滑移值也比较接近;曲线在经过下降段后,钢管的“宏观偏差”使得曲线发展趋势不一致,从而导致峰值点后有些试件的计算曲线和试验曲线有偏差.
3 结语
根据已有文献试验结果提出了高温下界面黏结应力-滑移关系曲线,通过对试验结果的分析,确定了影响恒高温下界面平均黏结强度的主要因素;利用回归方法,获得了恒高温下界面平均黏结强度和对应的滑移,剩余黏结强度与主要影响因素的关系式.计算结果与试验结果对比表明该模型适用性强,可为进一步研究钢管混凝土耐火性能的精细化有限元分析提供参考.

