基于方形邻域和裁剪因子的离群点检测方法

涂晓敏，石鸿雁

(沈阳工业大学，沈阳110870)

1 引 言

离群点检测是数据挖掘领域中的一项重要挖掘技术，主要目的是消除数据中存在的噪音或者挖掘出潜在的、有意义的知识[1-3].目前，离群点检测广泛地运用于诸多领域，如医疗处理、公共安全、图像处理、视频网络监视和入侵检测[4-6]等，具有良好的应用前景.

迄今为止，在离群点检测研究方面已经取得了一些成果，其中基于密度的离群点检测算法是最为著名和实用的方法.Breuing等[7]提出了局部离群因子算法(LOF)，借助于可达距离、可达密度和局部离群因子来判断离群点，使得对离群点的检测不再是二元结果.在数据分布异常情况下，计算数据对象与其邻域内数据对象的距离时，导致时间开销很大，且检测精度通常受给定参数的影响.Malik[8，9]提出了局部稀疏系数算法(LSC)和改进的局部稀疏系数算法(ELSC)，省去了LOF算法中可达距离、可达密度的计算，并引入裁剪系数的概念，并用局部稀疏系数代替局部离群因子表示对象的离群度，降低了计算的复杂度，但在剪枝过程中易导致部分正常点的误判.贾晨科等人[10]提出了局部孤立系数算法(LOC)，改进了LSC算法中局部稀疏率和局部稀疏系数的计算，并从数据集中选出具有最大局部孤立系数值的前n个对象作为孤立点，提高了检测效率.周云峰[11]提出了一种新的高维空间中离群点检测算法(NELSC)，在ELSC算法的基础上采用DBSCAN[12-14]聚类的方法对数据集进行预处理，去除属性权值低于阈值的对象，在预处理时算法对参数的敏感度较大.黄添强等[15]提出了基于方形邻域的离群点查找新方法(ODBSN)，吸收DBSCAN算法和基于网格[16]算法的优点，将邻域改为方形邻域并只对有数据分布的空间进行划分，克服了“维灾”问题，但在计算局部偏离指数时容易导致正常点的丢失.

由于基于密度的算法计算时间复杂度较高，并只适用于一定规模的数据集，在遇到大规模数据集时通常查准率较低.因此，本文在ELSC算法的基础上，提出了方形邻域和裁剪因子相结合的方法，采用方形邻域，减少邻域查询次数，可以快速找到候选离群点，降低了时间复杂度.引入新定义的裁剪因子进行候选离群点的精选，发现更多有意义的离群点，提高了算法的准确度.

2 ELSC算法

ELSC算法通常用来减少数据集的规模，不再计算所有数据点的离群程度，主要分为初选和精选两阶段进行，其思想是：

1)吸取基于密度算法的思想，根据邻域内数据对象的稠密程度，得到作为候选集的前提条件.

2)采用裁剪系数将不可能是异常点的数据对象进行修剪，剩余的对象构成候选集合.

3)对候选集中每个数据对象依次计算局部稀疏系数，并与阈值进行比较，确定最终的异常点.

ELSC算法中，在缩小了待测数据个数的同时，也存在不足之处：

1)有效性.对大规模数据集而言，异常点仅占数据集的很小部分，即便采用裁剪系数的方法，也只能排除一小部分数据对象，导致算法的精确度低.

2)执行效率.由于每个点在邻域查询时，都需扫描整个数据库，限制其在海量数据集中的应用.在计算邻域距离的过程中，数据对象之间需互相比较，对有n个数据的对象，则比较次数为(n/2)·(n-1)，对于一个K维的数据集，时间复杂度为O(Kn2)，离群点排序的时间复杂度为O(nlogn)，计算裁剪系数的时间复杂度为O(n)，因此算法的整体时间复杂度为：O(Kn2)+O(n)+O(nlogn).尽管采用R树等索引技术来提高查询效率，并不能从根本上解决问题；另一方面，当数据集维数较高时，R树等索引结构比顺序遍历的效果更差，无法提高算法的效率.

3 改进算法概念及主要思想

为了便于描述、直观理解，下文以二维空间为例进行介绍，这里一个点表示一个数据对象，故点与数据对象不再加以区分.

3.1 算法相关概念

给定一个二维数据库D，实参数e(方形邻域的边长).

定义1. 以p(x,y)为中心，e为边长的方形区域内的对象集合，称为p的方形邻域[17]，记作SSNeps(p)，即

{p′(x′，y′)∈D‖x′-x|≤e/2，|y′-y|≤e/2}

定义2. 与方形邻域S相邻的其他8个方形邻域的集合，称为邻近方形邻域[18]，记作Ne(S).如图1所示.

Ne(S)={S1，S2，S3，S4，S5，S6，S7，S8}

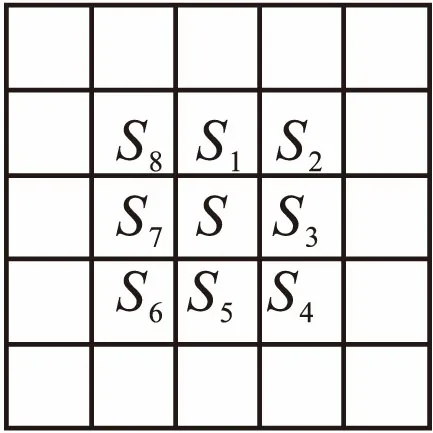
图1 邻近方形邻域示意图Fig.1 Adjacent square neighborhood diagram

定义3. 对象p的局部稀疏率lsr(p)

(1)

该式表示了数据对象邻域内大致的稠密程度，此处的距离为两个点之间的欧氏距离.

定义4. 对象p的裁剪因子PF

(2)

该式表明了整个数据集的平均密度.根据裁剪因子的值，将局部稀疏率明显小于裁剪因子的数据对象加入到候选集中.

定义5. 对象p的局部稀疏指数LSI(p)

(3)

从局部稀疏指数计算公式可知，若点p的邻域内数据对象的局部稀疏率平均值越大，而p的局部稀疏率越小，则LSI(p)取值将越大，若其值大于某个阈值T(T为大于1的值)，那么将点p记为离群点.

3.2 算法思想

为了降低时间复杂度和提高检测精度，本文将方形邻域和裁剪因子结合在一起，算法分为粗选和精选两个阶段，其主要思想如下：

1)粗选阶段：算法首先任选一个点，计算其方形邻域.若方形邻域内的点数大于邻域中邻居个数的阈值，则此方形邻域内的所有点为聚类点；否则方形邻域内的所有点为候选离群点.然后在该方形邻域周围任选一个方形邻域进行类似的操作，直到该方形邻域及其邻近的八个方形邻域中的所有数据点全部处理完毕.接着再任意选取一个尚未访问的数据点开始，重复上述操作，直至把所有的点划分为聚类点和候选离群点为止.

2)精选阶段：采用改进的裁剪因子对候选集中的对象进行筛选，再通过新定义的局部稀疏指数计算得到最终的离群点.

3.3 算法实施步骤

输入：数据集D，方形邻域边长e，邻居个数阈值MinP，邻域k，阈值T

输出：数据集D的离群点

I粗选阶段：

a)采用方形邻域的方法将数据集分为了聚类点和候选离群点并分别标记.

II 精选阶段：

b)根据公式(1)，计算候选离群点集中每个数据对象的局部稀疏率.

c)根据公式(2)，计算候选离群点集中每个数据对象的裁剪因子，并与局部稀疏率进行比较，得到最终的离群数据集.

d)根据公式(3)，计算最终离群数据集中数据对象的局部稀疏指数.

e)将局部稀疏指数大于离群因子阈值T的点判断为离群点.

3.4 时间复杂度

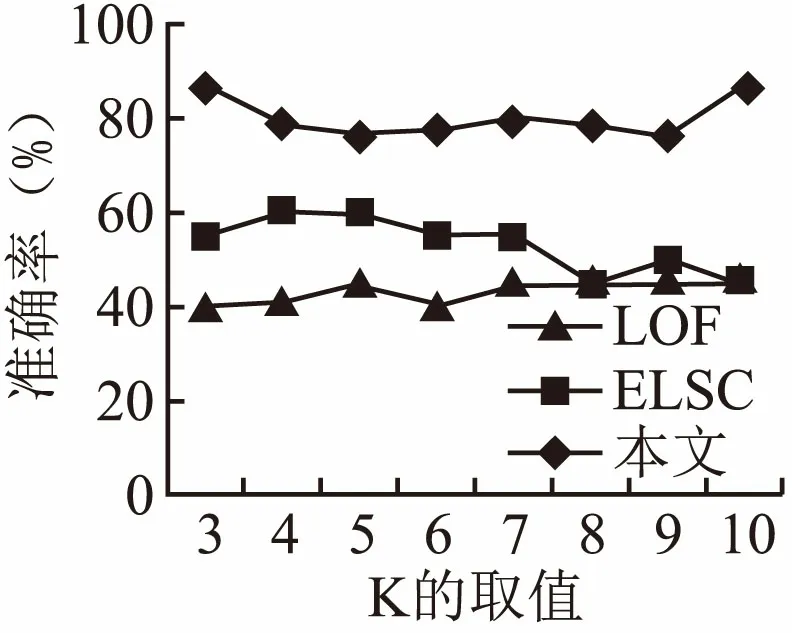
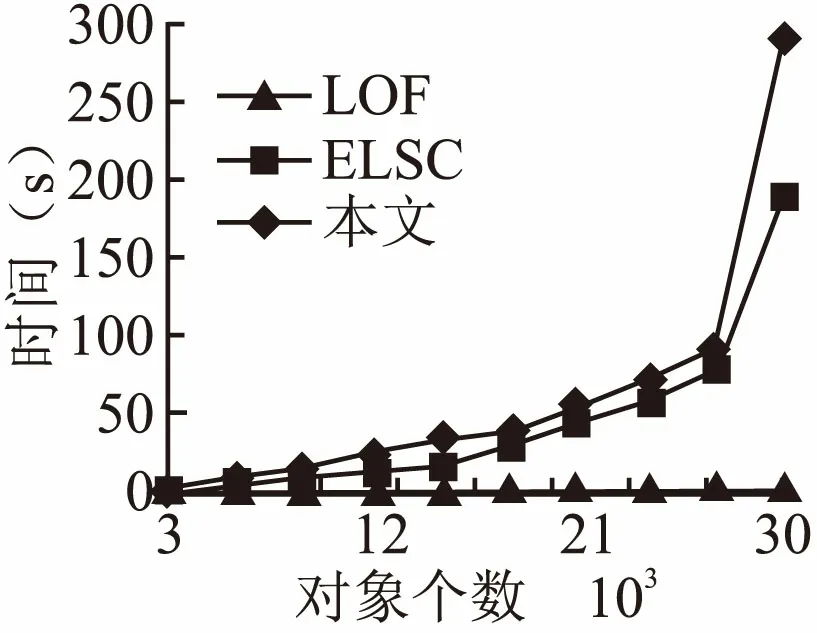
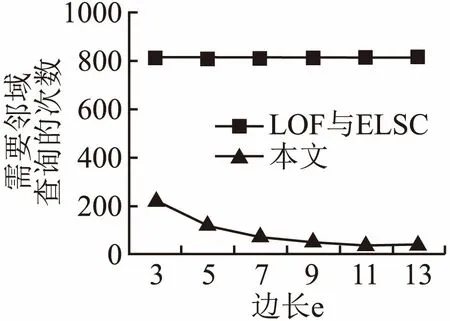
算法在邻域查询时最为消耗时间，一般情况下，邻域查询操作的时间复杂度为O(n)，若采用空间索引技术，可以将复杂度降为O(logn).本文算法在粗选阶段用方形邻域对空间进行分割，精选阶段对候选异常点进行k近邻查询，以求得裁剪因子PF.当数据集有n个对象，密集的方形邻域有m个，候选离群点个数为h(h<

4 实验分析

为了检验算法的性能，将本文算法与LOF算法、ELSC算法进行比较.其中实验选取了聚类基准数据集中的两个数据集并向其添加一定量的离群点(如表1)和随机生成服从正态分布的数据集，所有算法均在Matlab R2016a中实现，操作系统为Win7 Inter®CoreCPU 3.40GHz.

表1 数据集信息描述Table 1 Information description of dataset

4.1 实验有效性

为了检验算法的有效性，对R15数据集进行实验，它包含15个簇与20个离群点，图2为在参数k取不同值时，LOF算法、ELSC算法、本文算法的对比图.算法的准确率是采用几组数据的均值，从图中可以看出，本文的算法一直高于LOF算法、ELSC算法.因此，算法具有可行性.

图2 不同算法的精度对比Fig.2 Accuracy comparison of different algorithms

如图3为算法对R15数据集在粗选阶段划分的方形邻域.

图3 算法粗选阶段的方形邻域划分Fig.3 Square neighborhood partitioning in rough selection stage of algorithm

4.2 算法执行效率

为了验证算法的执行效率，实验采用随机数发生器产生服从正态分布的具有不同密度的聚类数据集，数据集大小从3000到30000不等.本文算法参数e=20，MinP=8，T=1.1，LOF算法中MinP=10，ELSC算法中k=80.由图4可知，本文算法的执行效率明显高于LOF算法、ELSC算法，虽然对象个数有所增加，但是算法的执行时间增幅不明显，故具有很好的可伸缩性.

图4 不同算法的执行时间对比Fig.4 Execution times of different algorithms

用Aggregation数据集进行邻域查询次数与边长e之间关系的实验，如图5所示，LOF算法、ELSC算法需对每个数据对象进行邻域查询，所以呈直线形.而本算法因为采用了方形邻域的方法，所以查询次数随着方形邻域边长e的增加而逐渐减少，并且比LOF算法、ELSC算法成倍地减少了邻域查询次数.

图5 邻域查询次数与边长e之间的关系Fig.5 Relationship between the number of neighborhood queries and side length e

5 结束语

本文研究了基于密度的离群点检测算法的不足，提出了一种基于方形邻域和裁剪因子的离群点检测算法.该算法不再对所有的点进行离群度检测，而是通过采用方形邻域的方法，快速排除密集邻域部分，再利用裁剪因子对候选离群点集中的对象进一步筛选，排除被误判的点，最后通过局部稀疏指数确定对象是否为离群点.实验结果表明，算法能有效的识别离群点，并在执行效率上有明显的优势.但是本文的研究工作仍需继续进行，未来将该算法推广到动态数据集中.