长度分布悬殊的序列比对法

陆 成 刚

(浙江工业大学 理学院,杭州 310023)

1 引 言

动态时间规整算法(Dynamic Time Warping,DTW)是一个经典的时间序列比对算法,最早被应用于短词语音识别的研究[1].自DTW距离被引入到一般时间序列的模式分析领域后[2],它已经成为经典的模式相异(似)性度量技术,并在近些年也屡获关注和研究[3-7].对于DTW技术的研究主要分为以下几类:

1)对于快速DTW计算方法的研究[7-12],例如考虑线性时间算法;

2)对于DTW有效改进的研究,如导数DTW算法(简称DDTW)[13];

3)基于DTW距离的矢量均值中心的计算[14,15]、或多个序列之间的DTW比对[12],其研究目的是考虑将DTW用于均值聚类.

DTW算法是计算序列之间动态对应意义下的最小距离值,与常规的静态对应下的序列距离计算相比,该方法有一些突出的特点:

1)它不仅能计算两段长度相同的序列间距,而且能计算长度不同的序列间距;

2)虽然它不满足传统距离的三角不等式法则,但在处理时长伸缩变异的序列时有传统距离不具备的特效.

例如,对于序列(a,b,b,a)和(a,a,b,a)如果依照传统的距离(取范数为1的欧式距离)计算为|a-b|;采用DTW距离计算则为0.零DTW距离表明这两个序列是相同序列,这种自动“隐藏、忽略”足标间隔时长不一的技术在工程上是非常有用的.但传统的DTW距离也隐含着一种缺陷,例如考虑使用DTW距离计算以下三段直流信号的匹配情况:A=(0.1,0.1)、B=(0.25,0.25,0.25,0.25)、C=(0.28,0.28,0.28),信号A与B的DTW距离为0.6,其最优匹配路径的长度为4;而信号C与A的DTW距离0.54,最优匹配路径的长度为3.从我们直觉判断信号B比信号C更接近A,但从DTW距离决定的相异性来看,反而是C比B更接近A.造成这个反直觉的效果是由于我们仅仅考虑了距离,而忽视了路径长度,假如以DTW距离相对路径长度的平均值而言,B比C更接近A.

虽然DTW算法处理长度不一致的序列间的距离计算是它的优势,但所谓“成也萧何,败也萧何”,在参与比对的多对序列之间由于各对最优路径长度的不一致造成对“距离大小决定相异程度”准则的干扰.上例两条路径长度只差1就显示了这种干扰,一般来说,当长度相差剧烈时这种干扰发生的概率更高.显而易见,如果将DTW作内置距离实现kNN最近邻法的序列匹配时,这种缺陷将造成致命的匹配错误.由此本文设计研究一种祛除路径长度因素的DTW距离,称为均值DTW.后文第2节将建立均值DTW的组合优化的目标函数,这是一个DTW的非平凡推广,该节将重点分析实现优化的算法;第3节将考虑受加窗限制时的均值DTW的处理方式,与常规DTW加窗形式有显著的不同;第4节给出均值DTW和常规DTW的算法实验比较,最后第5节对整个工作进行总结.

2 均值DTW

假设两段离散信号S=(s1,s2,…,sn)和H=(h1,h2,…,hm),设任意匹配路径函数P=(p1,p2,…,pl),其中pi=(qi,ri),而1<=qi<=n,1<=ri<=m,DTW路径函数满足单调性、连续性、边界值等性质,即:

1)对相邻两点pi+1=(qi+1,ri+1)和pi=(qi,ri)满足qi+1≥qi且ri+1≥ri;

2)对相邻两点pi+1=(qi+1,ri+1)和pi=(qi,ri)满足qi+1=qi或qi+1=qi+1且ri+1=ri或ri+1=ri+1,但qi+1=qi和ri+1=ri不同时满足;

3)p0=(1,1)且pl=(n,m).

也可以对路径函数提出窗口、斜率等限制要求.

常规DTW的缺陷是没有考虑路径长度平均的距离,从而可能导致两个同类序列的距离大于两个异类序列的距离.这就违背了“距离大小决定相异程度”的准则.定理1从理论上揭示了这种可能.

定理1.设对于序列S1其采样周期为T,先将S1使用sinc插值恢复成模拟信号,再使用T/n的采样周期离散化形成序列S2,S2长度n倍于S1、但两者仍属同类序列,可证S1和S2的DTW距离随着n的增加而无限制增加,势必将大于S1与任一确定的其它类序列H的DTW距离.

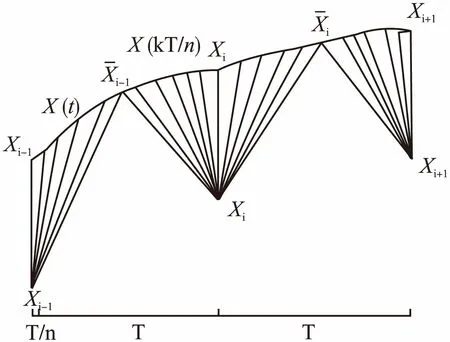
图1 信号重构采样后的DTW匹配Fig.1 Signal reconstruction resampled DTW matching

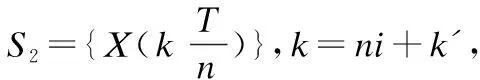
为克服常规DTW的缺陷,在满足以上路径条件1、2、和3的基础上提出均值DTW的最优路径问题：

(1)

其中距离函数d可以是范数1的欧式距离,也可以是平方欧式距离.在DTW的原始文献[1]中优化目标函数除以常数l,取l=n、l=m或l=m+n任定.因为是常数所以之后的文献中往往忽略这个值,然而既便除以常数仍难以保证祛除路径长度的干扰,这从引言例子的l如取作信号A的长度便可知.目标优化问题(1)考虑各种路径下的平均距离取优,由于路径长度随着路径不同而不同,一般而言l不是常数.通过简单的组合计算可以得到路径长度l的变动范围max(m,n)≤l≤m+n-1.

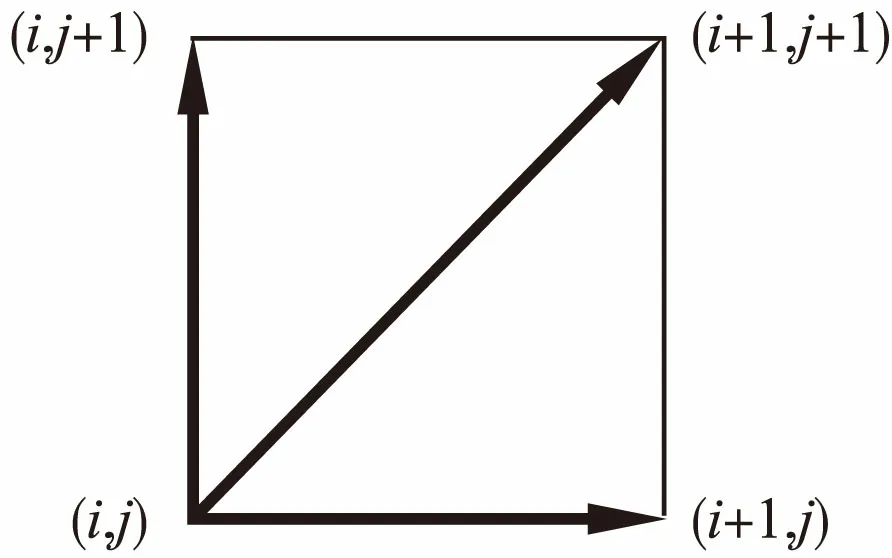
图2 动态路径延展示意Fig.2 Dynamic path zigzag display

当前点(i,j)延展到下一点时并不是直接取{(i+1,j+1),(i+1,j),(i,j+1)}中的距离最小值,而是将它们逐一考虑进全局路径的距离总量,而后取平均值中最小者对应的点.一个直接的思路是先定出一条完整路径再计算它对应的平均距离,并且枚举所有的路径就能找出最优均值及其对应的路径.

2.1 DTW路径数目

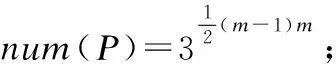
num(p0)=1

num((q,1))=num((q-1,1)),q=2,3,…,n;

num((1,r))=num((1,r-1)),r=2,3,…,m;

num((q,r))=num((q-1,r))+num((q,r-1))+num((q-1,r-1)),q=2,3,…,n且r=2,3,…,m;

最后输出num((n,m))为路径的数目.该算法成立的原理可以使用图3作示意.

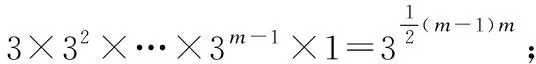
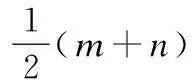
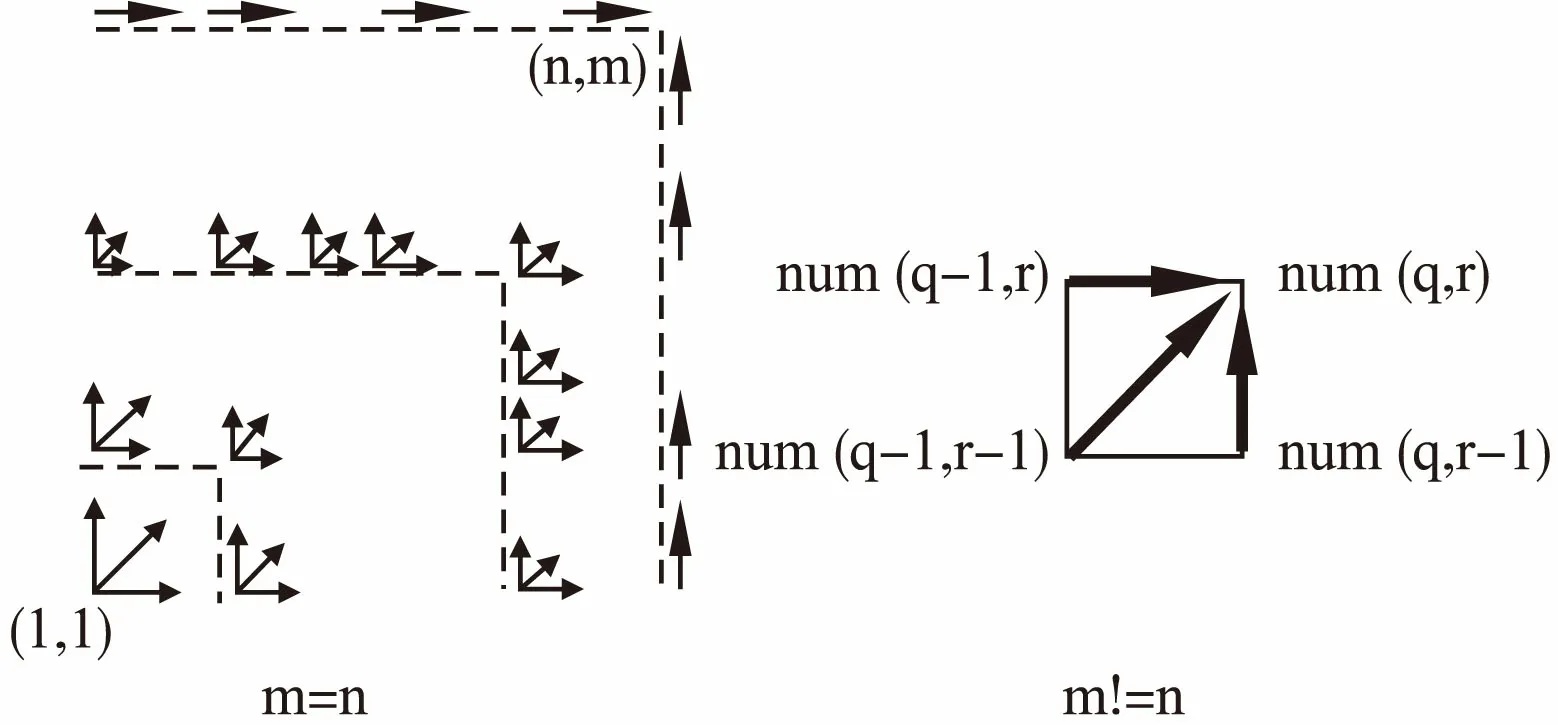
图3 路径计数原理Fig.3 Path counting principle

表1 DTW路径数目的指数增长
Table 1 Exponential increase in the number of DTW paths

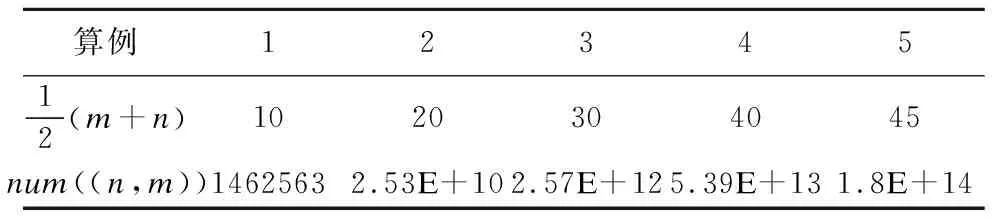
算例1234512(m+n)1020304045num((n,m))14625632.53E+102.57E+125.39E+131.8E+14

2.2 均值DTW解法

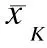
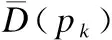
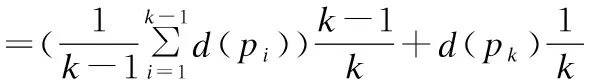
(2)

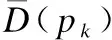
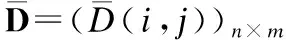
2.3 计算示例

如图5示例同类序列间由于长度相差悬殊导致DTW距离反而比不同类序列大,同时均值DTW却能抵制这种失效.

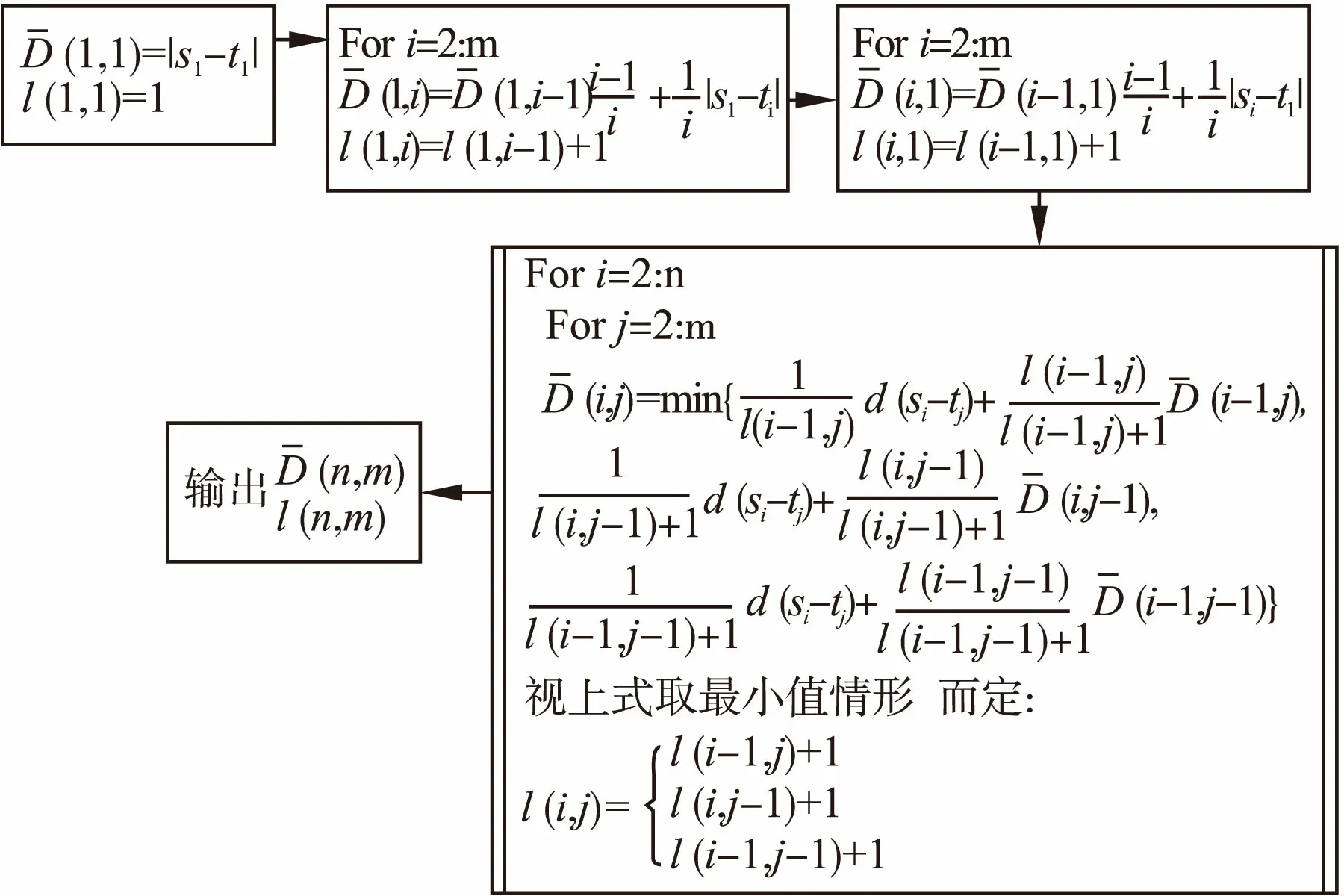
图4 均值DTW算法Fig.4 Mean DTW algorithm

图6例举了两个序列按照DTW、均值DTW匹配得到的路径:细实线代表DTW方法、粗点虚线代表均值DTW方法.

图5 DTW距离失效,而均值DTW有效的实例Fig.5 DTW distance failure,and the example of the mean DTW is valid

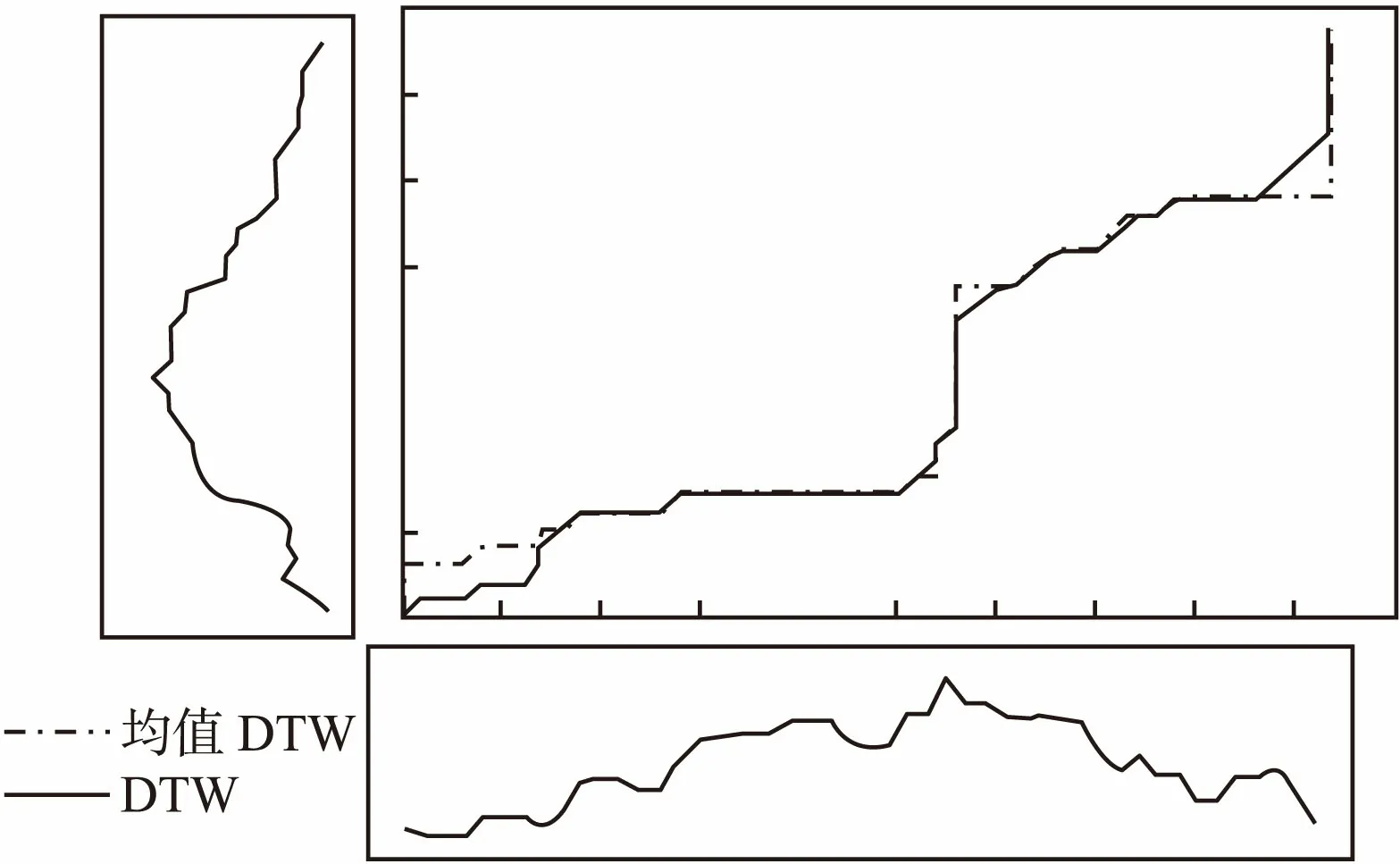
图6 DTW和均值DTW计算示例Fig.6 DTW and mean DTW calculation example

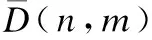
表2 DTW、均值DTW对比
Table 2 Comparison of DTW,Mean DTW

距离平均距离路径长度DTW43.710.70562均值DTW46.857980.65080572

由表2可知从平均距离的角度看均值DTW小于常规DTW,而从(总值)距离的角度看DTW小于均值DTW.这是自然的、且符合这两个概念的设计初衷的.最后讨论均值DTW路径长度与常规DTW路径长度的关系.

定理2.对序列S=(s1,s2,…,sn)和H=(h1,h2,…,hm)它们的DTW距离对应的路径长度必不长于均值DTW对应的路径长度.

表2给出的例子显示均值DTW的路径长度大于DTW距离的路径长度,定理2说明这是必然的.

3 均值DTW的加窗机制

图7 均值DTW算法加窗限制Fig.7 Mean DTW algorithm windowing limit

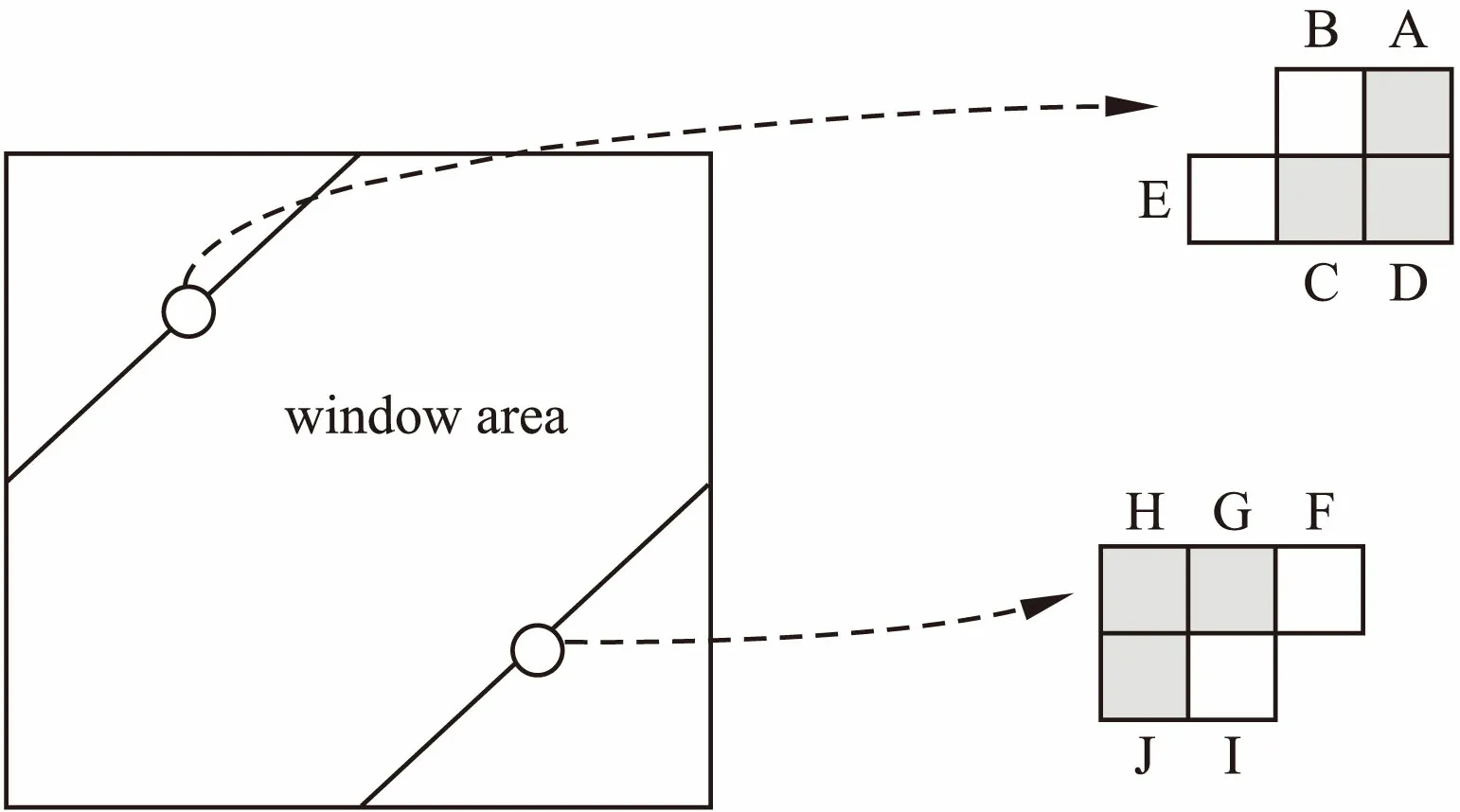
图8 “紧贴”窗口区域的外部点l值更新原理Fig.8 Principle of external point l value update in the “close to”window area

图9给出图6对应的比较实例在应用了加窗机制后的情形,窗口大小为10.表3给出该情形的距离值的对比.

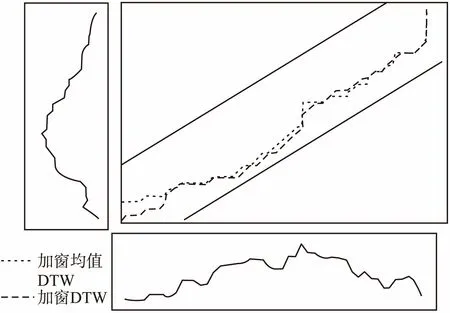
图9 DTW和均值DTW的加窗计算结果Fig.9 Windowing calculation results for DTW and mean DTW

表3与表2对比可见无论是常规DTW还是均值DTW,加窗处理会导致对应的平均距离值有所升高,这是因为加窗后的匹配范围缩小了的缘故.此外,在加窗情形下就平均距离而言均值DTW依然是低于DTW,且路径长度长于DTW.

表3 加窗计算的对比
Table 3 Comparison of windowing calculations

距离平均距离路径长度DTW54.861010.97966156均值DTW60.499550.9166666

4 实验与结果

实验分析数据使用电离辐射时间序列,它们是取自于核电站周边的环境辐射监测仪.核电站环境辐射检测数值通常和降水、风向等天气因素有关,这是由于地球大气层微粒吸收源自太空的高能粒子的电离辐射能量,通过雨、雪、风等各种气象状况聚集于地表.所以研究核电站的环境背景电离辐射离不开对于降水导致的辐射剂量异常的分析和识别,是精确分析、检测由核电泄漏事故引发的剂量异常的基础.核辐射监测时间序列分析需要实时检测辐射剂量波峰、以及识别波峰的具体类型(不同的气象气候所致、或者核泄漏事故等).此外,核辐射检测仪器故障自动重启、分布式监测网络数据传输中断等设备异常会造成核辐射时间序列夹杂一定的随机外点或噪声.

本文采用的算法有层次聚类、kNN分类,它们都可以使用DTW或均值DTW作内置距离,数据是已经人工标注的序列,因而便于验证算法效果.聚类分类是模式识别的核心问题,常用的方法有k均值聚类、模糊c均值聚类、层次聚类、kNN最近邻法分类、PCA、谱聚类、DBSCAN以及深度学习神经网络,等等.如何判断模式之间的相似(异)性又是聚类分类的核心问题,DTW距离是聚类分类、模板匹配的经典的技术之一.对均值DTW算法与常规DTW作比较,分别植入层次聚类、和kNN最近邻法进行标注数据集的聚类分类测试.

实验采用4907条人工标注的共分为4个类别的核辐射波峰片段,它们被分为三个集合:集合A含有2324条4类别波峰段,序列段长的平均值为274.9、长度分布标准差为174.1;集合B含有1974条4类别波峰段,段长平均为194.4、标准差为5.7;集合C含有609条4类别波峰段,段长平均为186.1、标准差为178.3.此外集合C与A、B不同,几乎每一条都含有随机外点的成份,而集合A、C有一个共同点就是信号长度分布的悬殊程度较B更为剧烈,这容易从它们的长度标准差数值得知.实际上在核辐射检测中一方面由于剂量上升异常所持续的时间长度确实不一,有时候差别甚为巨大(例如不同时间长度的持续降雨,等等);另外一方面,由于波峰提取阶段所用技术的限制导致有些波峰段提取显得较为“紧凑”、有些则含有较长的两端低幅度延伸部分.图10示例了A、B集合的少部分4种类别的波峰段,图11示例了C集合的带外点的波峰段,外点发生比较随机,幅值可能突然上升,也有可能突然下降.

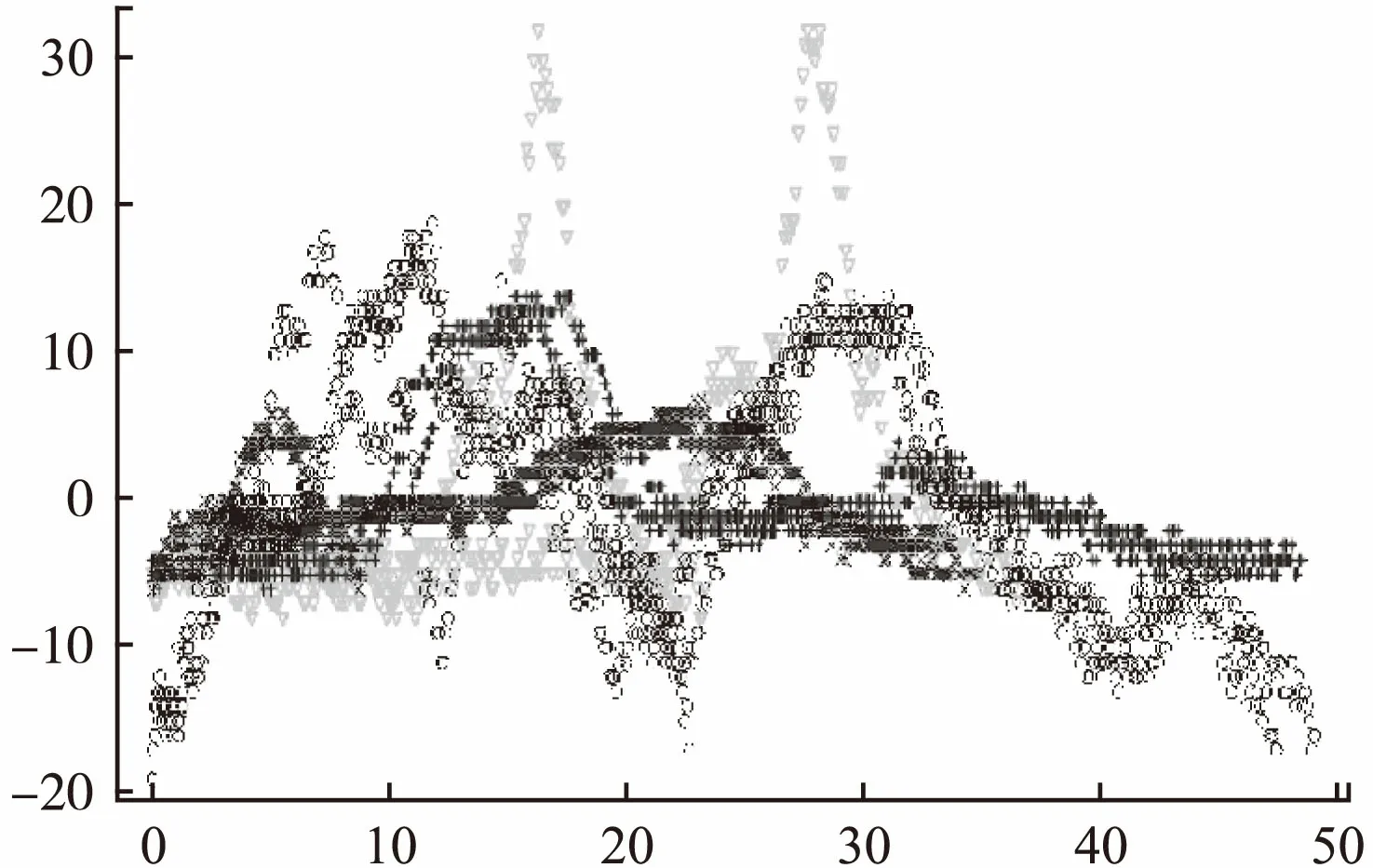
图10 集合A、B少部分的波峰段示例,分别以“▽+xo” 标记4种类型Fig.10 Example of a peak segment with a small number of sets A and B.Mark 4 types with "▽+xo" respectively

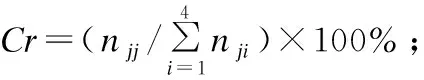
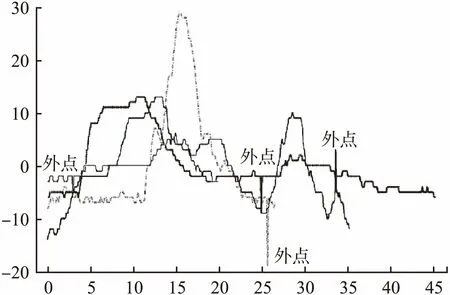
图11 集合C的4种含外点的波峰段类型示例,其中3个外 点是突降型,另外一个突升型Fig.11 Example of four types of peak segments with outlier in Set C,three of which are dip-type and the other is a sub-type

图12给出了对集合A、B作层次聚类所得的计数矩阵(nij)4×4的三维柱状图,对集合B在波峰长度变化不悬殊时(长度分布标准差较小),常规DTW和均值DTW都能取到比较高的精度;当对集合A进行聚类时由于波峰长度相差较为悬殊(长度分布标准差较大),这时路径长度的不一致对DTW距离值的干扰较大,此时常规DTW近乎完全失效,而均值DTW还能取到较好的效果.表4列出图12计数矩阵计算的F值.

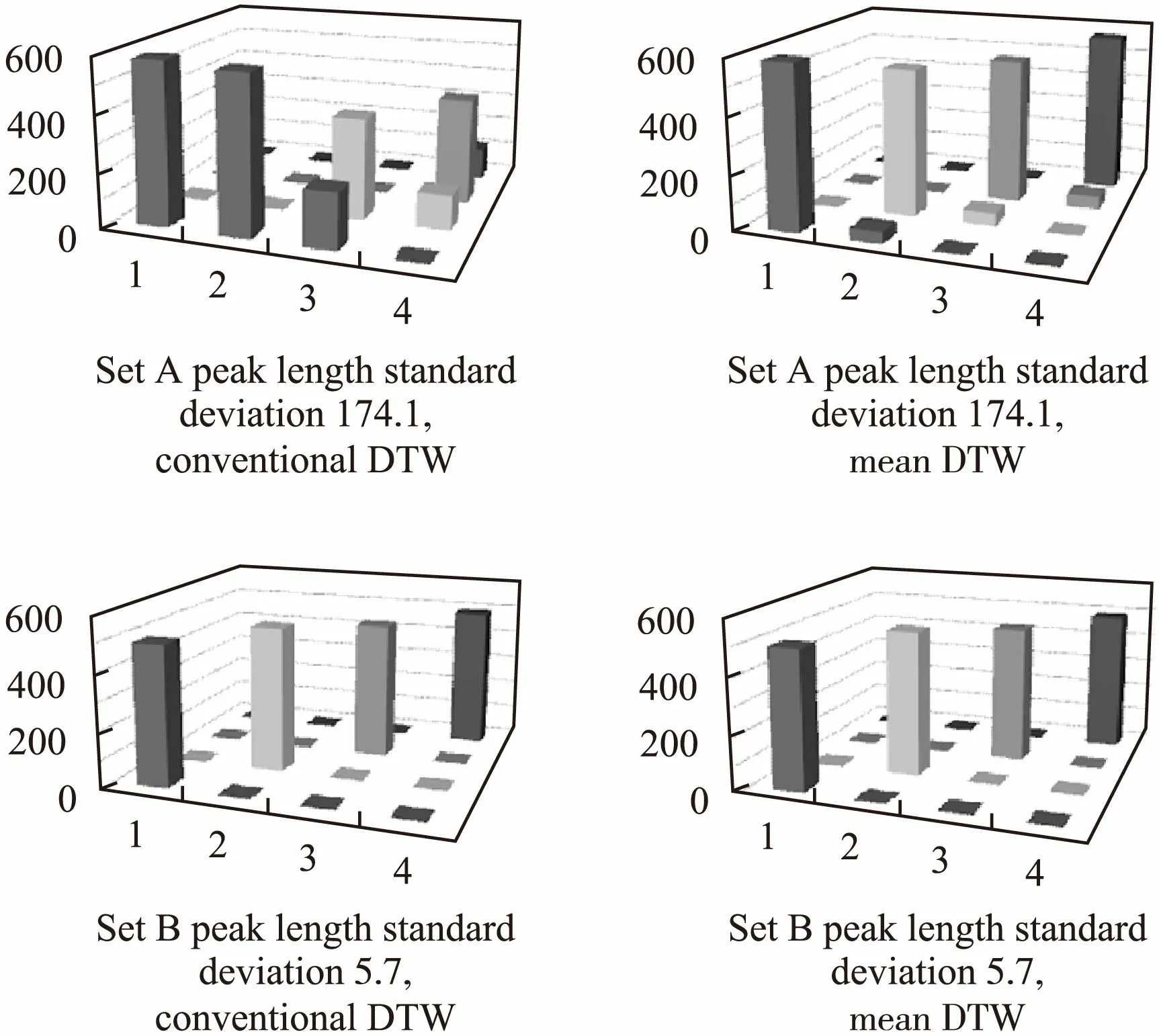
图12 集合A、B进行层次聚类的计数矩阵三维显示Fig.12 Three-dimensional display of the counting matrix for hierarchical clustering of sets A and B

由表4可见在数据集A上使用均值DTW至少比使用DTW(对类别1而言)提升了精度达50%以上.

表4 两类数据集的算法效果F值
Table 4 Algorithmic effectFvalues of two types of data sets

表5 对集合C进行kNN近邻法分类的定量分析
Table 5 Quantitative analysis ofknearest neighbor classification for set C

从表5看出在集合C所含具有较悬殊的信号长度差别的动态特性下,将常规DTW和均值DTW用于kNN模式分类时,后者的识别精度显著地优于前者.

5 总 结

对于模式聚类分类而言,在研究强有力的分类逻辑和机制中,离不开对数据统计规律的建模,同时对数据寻找有效的相似(异)性度量技术也是一个绕不开的课题.DTW算法因对时间序列时长节奏的伸缩性有极佳的适应性而被广泛使用,常规DTW算法常常忽略路径长度不一致所导致的对距离值的干扰,这在一定程度上抑制了DTW对长度相差悬殊的序列数据集的适用性.该文的研究工作从单位路径长度的距离值的组合目标优化出发,给出了捕捉最小平均距离的DTW对齐方式,并将此用作时间序列相似(异)性的度量方法.该方法较常规DTW在聚类分类上有显著的精度改善.它和常规DTW有等价的计算复杂度,只在内存消耗上比常规DTW增加一倍.将来可以考虑在最优路径搜索中融合自动变系数的二阶IIR滤波机制,以避免存储路径长度矩阵的内存占用,并探讨这样处理给高含噪量的时间序列动态匹配带来的积极作用.