安全C语言验证器中形状系统的形状检查方法

孙 科,罗奇鸣,李薛剑,陈意云

(中国科学技术大学 计算机科学与技术学院,合肥 230026)

1 引 言

1.1 研究背景

随着计算机技术的发展,各行各业与计算机软件的关系日益紧密,且软件的规模和复杂度也在不断增加,在这种大背景下,整个行业对于软件的可信度提出了更高的要求,尤其是安全攸关的领域.遗憾的是,许多程序设计语言在发展的同时,并未在语言的安全层面提供太多保障,典型代表就是C语言.

对此,多种基于不同切入点的工作正在稳步进行.在程序设计语言层面,Rust作为一门新兴语言,在编译过程中引入了诸多概念,约束程序的行为,以期在程序编译期间尽可能发现内存、数据竞争等方面的问题;SPARK[1]则是一门基于Ada语言的形式化定义语言,它将形式化方法引入软件的设计中,藉此提升软件的可信度.而对于既有的程序设计语言,基于演绎推理的形式化验证则是提高软件可信度的重要方法,例如Ynot[2]、Spec#[3]、ESC/Java[4]等.本课题组面向C语言开发了一套基于演绎推理的程序验证工具——安全C语言验证器(以下简称“验证器”),该验证器基于霍尔逻辑[5]和形状图逻辑[6,7].

1.2 研究目的

基于演绎推理的验证工具大多基于如下实现:根据用户提供的函数前条件、后条件以及循环不变式,验证工具采用正向或逆向演算,将程序需要满足的性质转换为验证条件,后采用自动定理证明器实现验证.为解决霍尔逻辑难以处理C语言中由于指针带来的别名问题,安全C语言验证器采用形状图逻辑处理堆指针,将程序状态描述为G和Q,其中G表示描述指针性质的形状图,遵循形状图逻辑,Q表示描述程序其它性质的符号断言,遵循霍尔逻辑.形状系统是对于形状图逻辑的一个实现,主要用以限制利用动态内存分配和指针能够构造的易变数据结构的种类,并约束程序操作这些数据结构的行为.这里的易变数据结构指的是通过节点指针域实现连接的,结构完整性和节点个数等性质在程序执行过程中容易发生变化的数据结构,诸如链表和二叉树.形状系统的演算依赖于程序的操作语义,然而易变数据结构的常规操作容易造成易变数据结构性质的变化,其中不免对易变数据结构造成破坏,使其不符合指定的形状定义,例如双向链表的插入操作.

不符合形状定义的易变数据结构给形状系统带来了严峻的挑战,其一,对不符合形状定义的易变数据结构进行演算,是无法推断别名的一个重要根源,例如指针访问路径p->nxt悬空,此时寻找该路径的别名则是一个无意义的操作;其二,用户通过断言描述形状图,而断言的构造语义无法确保新构造的易变数据结构符合形状定义,例如可能存在用户错误描述形状图的情况,这将影响验证的正确性;其三,不符合形状定义的易变数据结构也是造成循环不变形状图自动推断操作[8,9]不终止的主要原因;其四,验证器依赖于Z3自动定理证明器[10]进行证明,而从不符合形状定义的易变数据结构中导出的指针关系通常是存在问题的,为Z3自动定理证明器的证明带来较大压力.

1.3 本文工作

本文工作基于安全C语言验证器的形状系统进行设计与实现,提出了形状检查方法,它能够对含有易变数据结构操作的C程序源码进行检查,判断相关程序点的易变数据结构是否符合形状定义.本方法在形状系统中分别实现了隐式形状检查和显式形状检查,前者由系统在重要演算点自动对易变数据结构进行形状检查,避免不符合定义的易变数据结构对形状图逻辑演算的正确性造成影响,后者允许用户在程序点主动指定需要形状检查的易变数据结构,以尽早发现其中的潜在问题,提升形状检查的灵活性和易用性.此外,形状检查方法采用3阶段处理框架,分解由于易变数据结构中指针域灵活指向带来的复杂性,降低算法实现上的难度.

本文的内容结构组织如下:第2节概述安全C语言验证器和形状系统;第3节介绍形状检查的相关概念;第4节详细介绍形状检查中多阶段检查的相关规则及算法;第5节通过实验检验方法的效果;第6节介绍相关工作;第7节进行总结.

2 安全C语言验证器及形状系统概述

本课题组基于霍尔逻辑和形状图逻辑开发了安全C语言验证器,实现对于符合安全C语言规范1的C语言代码的验证.验证器复用Clang/LLVM编译器的前端,将源程序与用户标注的断言转换为抽象语法树,由验证条件生成器遍历抽象语法树产生程序性质相关的断言,其中堆指针相关性质的演算与证明操作交由形状系统执行,其余验证条件交由Z3证明.目前的形状系统支持5种简单形状:单向链表、双向链表、循环单向链表、循环双向链表及二叉树.易变数据结构和形状之间的关系,可以类比于静态类型语言中变量和类型的关系.因此,在一定程度上,形状系统可以视为面向易变数据结构的类型系统,但两者又存在本质上的不同:

1)形状系统依赖程序的操作语义,而类型系统则是给出对程序代码的上下文相关的约束,不涉及语言的操作语义.

2)对于形状系统而言,指针指向的易变数据结构并不需要时刻符合形状定义,对于类型系统而言,某个类型的变量只能保存该类型的值.

形状系统通过图形形式表示易变数据结构的内存状态以及指针指向关系,包含6种不同类型的形状图节点[11]:圆形节点称为声明节点,表示程序中声明的指针变量;含N的虚线矩形表示NULL节点,用于描述对应指针为NULL;含D的虚线矩形表示悬空节点,用于描述指针悬空;实线矩形节点称为结构节点,表示动态分配的结构体单元;含e和a的灰底实线矩形称为浓缩节点,表示指定数量的结构节点的折叠,其中e为描述数量的表达式,a为关于e的约束断言;含P的实线矩形称为谓词节点,表示具有指定谓词性质的节点.通过上述的节点类型,可以构造如图1(a)中的单向链表及图1(b)中的循环单向链表,分别具有指针关系p->nxt->…->nxt == NULL和p->nxt->…->nxt == p,其中nxt重复e+1次,声明节点的出边表示指定名称的指针变量的指向,其它节点的出边表示指定名称的结构体域指针指向.

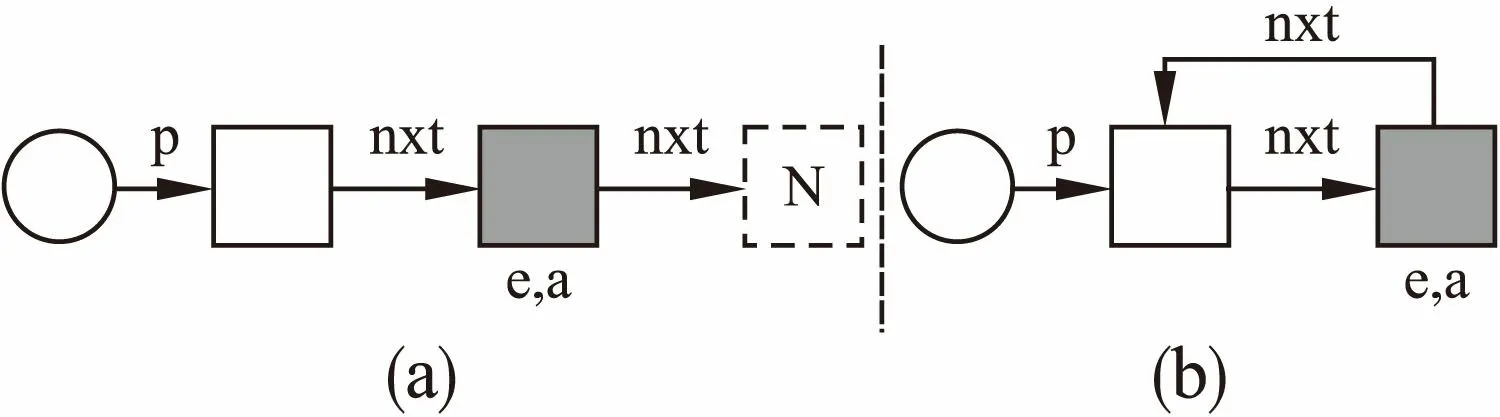
图1 易变数据结构示例Fig.1 Mutable data structure examples

安全C语言规范指定需要通过形状标注对程序中使用的堆指针变量或者结构体类型进行描述,以双向链表为例,声明如图2所示.形状标注通过注释的形式规避对于程序语义的影响,相关标注以“@”开头,“shape”表示该标注属于形状标注,其含义为该结构体的next和prev域共同组成双向链表的主形状域.出于扩展考虑,形状系统引入了嵌套形状域:次要形状域和共享次要形状域,例如声明中标注有“secondary”的域即为次要形状域.嵌套形状域用于描述多个简单形状的组合,本文将这类形状简称为嵌套形状.嵌套形状域存在如下性质:

1)独占性:一个易变数据结构仅能被一个嵌套形状域指向;

2)共享性:一个易变数据结构中所有节点的同名共享次要形状域只能指向同一易变数据结构的入口节点;

3)无环性:易变数据结构不能通过嵌套形状域构成循环指向.

其中共享性通过赋值演算中的不变式进行保证,不属于形状检查的内容.为明确表述,以下先行阐述下文中使用的名词:

1)前向主形状域:简称前向域,记作forward,是链表形状中浓缩节点展开的依据.

2)后向主形状域:简称后向域,记作backward,与前向主形状域共同组成双向链表的主形状域,单向链表和循环单向链表不存在该形状域.

3)非主形状域:对于声明节点域、次要形状域、共享次要形状域的统称.

4)主结构:仅由主形状域构成的易变数据结构.

5)次结构:主结构通过嵌套形状域指向的易变数据结构.

1 struct dlist {2 int data;3 struct dlist* next;4 struct dlist* prev;5 struct list* sub;6 }; //@shape prev,next:dlist,primary; //@shape sub:list,secondary;

图2 双向链表的声明
Fig.2 Declaration of doubly linked list

3 形状检查概述

形状检查即检查指针所指向的易变数据结构是否符合该指针声明所指定的形状定义的过程.类似于类型系统中关于类型的相容性检查,本方法引入3种不同的形状级别,表示形状检查的不同严格程度:

1)标准形状(STANDARD):最严格的形状级别,在易变数据结构符合形状特征(4.2节详细描述形状特征)的情况下,仅允许一个非主形状域指针指向易变数据结构,常见于函数的前形状图和后形状图;

2)可接受形状(ACCEPTABLE):除标准形状中所述,还允许其它非主形状域指针指向易变数据结构.常见于易变数据结构的各种操作中,例如通过额外的指针遍历链表;

3)待完善形状(UNACCEPTABLE):除标准形状和可接受形状之外,其余的易变数据结构均属于待完善形状.通常认为该级别的易变数据结构是不安全的.

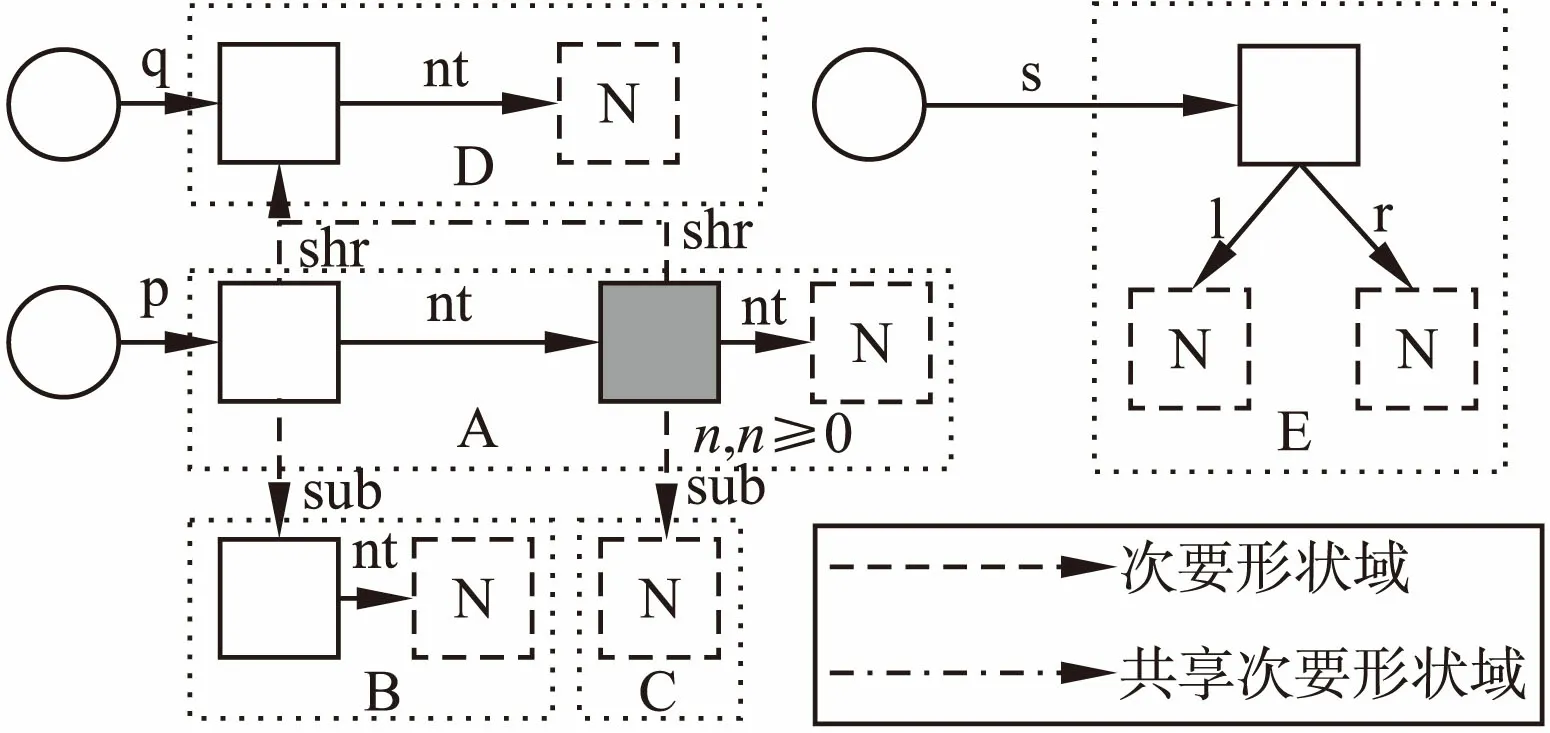
图3 复杂形状图示例Fig.3 Example of complicated shape graph

在较为复杂的程序中,主形状域和嵌套形状域共存,多种形状类别的易变数据结构共存的情况十分常见,如图3所示,这给形状检查的规则设计以及具体的算法实现造成较大麻烦.为此,如下对破坏形状定义的原因进行了分类汇总:第一,主形状域的错误指向或者嵌套形状域的指向破坏性质;第二,节点类型不满足约束;第三,非主形状域指向的节点不合要求或者主结构和次结构的形状级别组合冲突.

形状检查方法的总体思路为通过预处理分离形状图中不同的形状域,将其转换为便于处理的统一表述,并根据造成易变数据结构不符合形状定义的原因,通过多个阶段实现检查,每个阶段只需着眼于检查特定的内容,以达到控制算法及实现的复杂度的目的.如图4所示,形状检查方法的输入为含有待检查易变数据结构的形状图,输出为该易变数据结构的形状级别,将其与预期的级别进行比较,即可判断该易变数据结构是否符合形状定义.形状检查方法分为形状分割、形状分析和形状推断三个阶段,它们的作用分别为:

1)形状分割:对形状图进行预处理,将其中的主结构转换成形状元信息,并生成节点-元信息映射表供后续分析使用;

2)形状分析:依次通过形状间分析和形状内分析,分析由嵌套形状域和主形状域产生的指针指向关系以及节点位置对节点类型的约束,从而预先判断部分属于待完善形状的易变数据结构,将结果保存于结果表中;

3)形状推断:根据非主形状域指针的指向推断主结构的形状级别并结合其所有次结构的形状级别最终推断易变数据结构整体的形状级别.

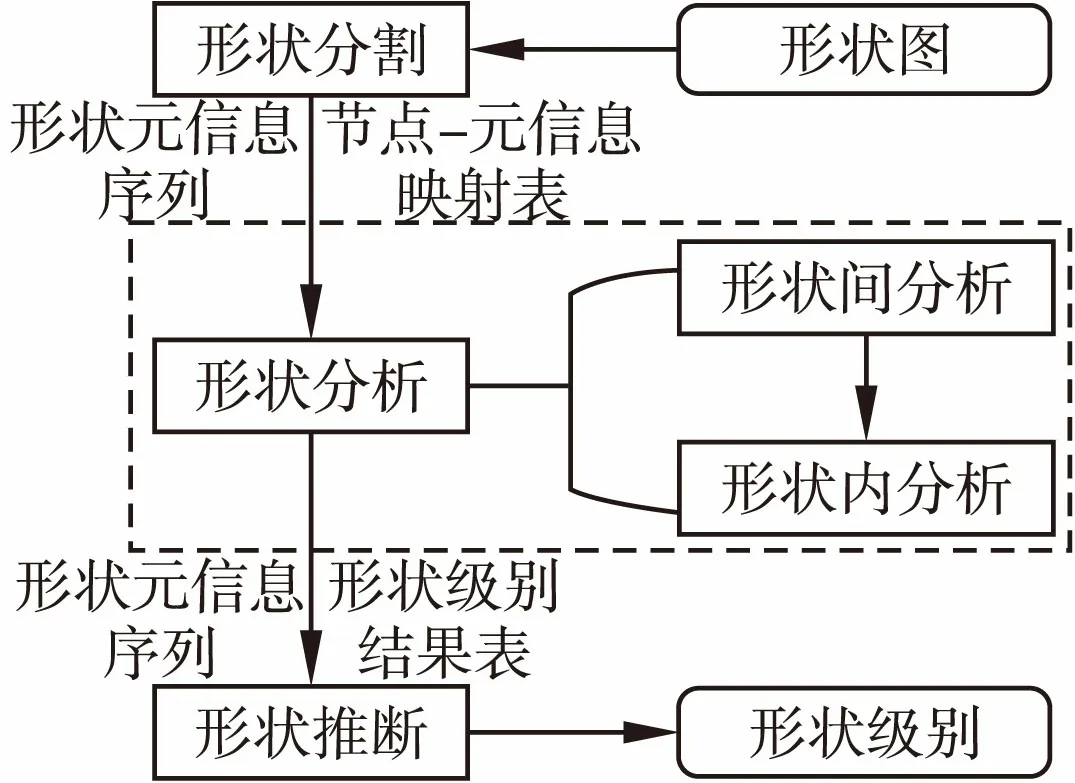
图4 形状检查方法总体流程Fig.4 Overall flow of shape checking approach

根据形状图逻辑理论,用户可以通过提供期望的形状图,凭借形状图的蕴含证明,检查易变数据结构是否符合形状定义.但在实际系统实现中,这类方式存在以下问题:其一,仅凭形状图断言的构造语义无法保证形状图构造的正确性,即无法保证蕴含式后件中的易变数据结构一定符合形状定义,因为用户亦可能会错误描述断言;其二,蕴含证明方法需要用户通过断言描述程序状态,繁琐且容易造成疏漏;其三,蕴含证明仅在几个固定的验证点进行,对于稍复杂的程序,不够灵活,且不利于尽早发现易变数据结构中的问题.

check ∷=check_shapecheck_selection check_selection ∷=shape_levelid(,id)*shape_level ∷=standard|acceptable

图5 形状检查文法
Fig.5 Grammar of shape checking

针对上述问题,本工作分别引入了隐式形状检查与显式形状检查,它们的实现均基于形状检查方法,区别在于触发检查操作的方式.隐式形状检查由系统在重要验证点进行自动检查,这类验证点包括函数入口、函数出口、循环入口、函数调用点等,主要用于确保新构造形状图中的易变数据结构符合定义,它们通常就是蕴含式后件中的形状图,除非用户特别指定,默认情况下确保所有易变数据结构至少为可接受形状.显式形状检查允许用户通过图5中定义的文法,在任意程序点对指定范围的易变数据结构进行形状检查,例如“check_shape standard p,q”表示检查指针p和q所指向的易变数据结构是否属于标准形状.相较于通过断言描述程序状态,然后依赖蕴含证明的方式检查易变数据结构是否符合形状定义,显式形状检查更具易用性和灵活性,且能够尽早发现易变数据结构的问题.

4 形状检查的具体方法分析

4.1 形状分割

形状分割指的是从形状图中分离主结构,并将其转换成形状元信息表述的过程.例如图3经过形状分割处理后,等效可得图中所标注的主结构A～E,但形状分割操作并不会丢弃由非主形状域表述的指针关系,而是将它们保存于形状元信息中.形状元信息表现为四元组,Type表示易变数据结构所声明的形状种类,Entry表示易变数据结构的入口节点集合,Src表示通过非主形状域指向该易变数据结构的节点集合,Dst表示当前易变数据结构的非主形状域指向的节点集合.根据嵌套形状域的共享性和独占性,Src仅保留共享次要形状域源节点中的入口节点.为便于后续分析工作根据节点获取对应的形状元信息,形状分割操作会导出节点-形状元信息映射表(以下简称节点映射表).

Input:Shape meta tuple T,shape node N,mapping from node to shape meta tuple M1 T.Type ← Get ShapeType(N);2 Q←CreateQueue();3 Enqueue(Q,N);4 while IsEmpty(Q)==False do5 cur←Dequeue(Q);6 if HasKey(M,cur)==Ture then7 continue;8 end if9 M[cur]←T;10 if IsEntryNode(cur)==Ture then11 Insert(T.Entry,cur);12 end if13 if HasNonprimaryField(cur)==True then14 Insert(T.Src,peer nodes of non-primarypoint-in fields);15 Insert(T.Dst,peer nodes of non-primarypoint-out fields);16 end if17 Enqueue(Q,peer nodes of the primary fields of cur);18 end while19 if Size(T.Entry)==0 then20 Insert(T.Entry,N);21 end if

图6 形状元信息填写算法
Fig.6 Algorithm of filling shape meta information

入口节点Entry作为后续阶段中遍历各易变数据结构的入口,是确保通过一次遍历覆盖易变数据结构所有节点的关键.对于所有形状而言,由非主形状域直接指向的NULL节点均可作为入口节点,其它情况下,不同形状种类的入口节点的判定存在区别:对于单向链表和二叉树,入口节点为主形状域入度为0的节点;对于双向链表,入口节点为前向主形状域入度为0的节点;对于循环单向链表和循环双向链表,入口节点优先选择嵌套形状域指向的节点,否则,任意声明节点指向的节点均可.需要特别说明的是,不符合形状定义的易变数据结构可能不存在或者存在多个入口节点.

显式形状检查通过标注指针变量的形式,约束待检查易变数据结构的范围,而隐式形状检查则默认检查所有易变数据结构,可认为其标注了所有指针变量.由于无法排除存在多个指针变量指向相同易变数据结构的可能性,因此它们仅可作为遍历易变数据结构的参考.据此,形状分割算法引入待遍历节点集合,初始即为标注中指针所指向的节点集合,依次根据其中的节点提取形状元信息.

形状元信息填充算法的本质为对由主形状域和节点构成的无向图进行广度优先遍历,并在遍历过程中完成对于形状元信息的填写.如图6所示,算法首先使用GetShapeType函数获取节点N所声明的形状类别,并保存到元信息的Type中.然后创建一个队列,将参数N对应的节点入队,第4行至第18行的循环为广度优先遍历的迭代过程,该循环将不断迭代直至队列为空.在循环体中,每次迭代均会从队首取出一个节点,判断该节点是否已访问,若映射表M中已经含有关于节点的键,则说明该节点为已访问节点,需要略过本次迭代,否则将节点到形状元信息的映射存入映射表M,标记该节点已访问.第10行至第12行的分支语句通过IsEntryNode函数判断当前节点是否为入口节点,若是,则将其作为元信息中的Entry.第13行至第16行的分支语句通过HasNonPrimaryField函数判断当前节点是否含有非主形状域,若存在,则通过第14行与第15行的语句分别提取非主形状域中的起始节点集合和目标节点集合,将它们分别存入元信息中的Src和Dst集合.在循环体的最后,需要通过主形状域提取下一节点,并将其入队.若在算法的遍历过程中,没有找到符合要求的入口节点,则默认将输入的节点N作为元信息中的Entry,由第19行至第21行的语句实现,形状分析阶段能够识别这种情况,并作出处理.

为覆盖所有仅含嵌套形状域指向的主结构,在每次填充元信息之后,需要额外将嵌套形状域指向的节点加入待遍历集合,如此即可实现等价于标注中存在指针变量直接指向该主结构的效果.

4.2 形状分析

形状分析是通过分析不同形状域指针的指向以及节点的类型,实现对待完善形状预先判断的操作,包含2个子阶段:形状间分析和形状内分析.

形状间分析是通过分析主结构之间由嵌套形状域构成的连接关系,确定对应易变数据结构是否属于待完善形状的操作.根据形状分割阶段导出的形状元信息以及节点映射表,可以构造有向图G(V,E),其中V为由形状元信息表示的主结构集合,E为主结构之间的嵌套形状域连接关系.

通过将主结构抽象成节点的形式,可以将图3中的形状图转换成图7中所示的有向图,其中由A指向B的边即表示主结构A存在嵌套形状域指向主结构B.根据嵌套形状域的独占性和无环性要求,可知符合定义的有向图是由多叉树构成的森林,这样就可将形状间分析转换为判断有向图是否为森林的问题.

图7 有向图示例Fig.7 Example of directed graph

如图8所示,算法根据SplitConnectedGraph函数完成对于依赖图的连通分量的划分,并保存于集合S中.然后通过第2行至第8行的循环遍历每个连通分量,通过IsPolyTree函数判断当前连通分量是否为一颗多叉树,若不是,则意味着易变数据结构无法通过形状间分析,需要通过第4行至第6行的循环遍历连通分量的每个顶点,并在结果表R中将它们所表示的易变数据结构标记为待完善形状,其中GetVertexSet函数用于获取图的顶点集.

Input:Shape dependency graph G and shape level table R1 S←SplitConnectedGraph(G);2 foreach g in S do3 if IsPolyTree(g)==False then4 foreach n in GetVertexSet(g)do5 R[n]←UNACCEPTABLE;6 end foreach7 end if8 end foreach9 return L;

图8 形状间分析算法
Fig.8 Algorithm of inter-shape analysis

形状内分析是通过分析主结构的形状特征,结合相应规则确定其是否符合形状定义的过程.虽然形状内分析仅关注主形状域,但是由于指针的灵活性,依旧存在大量不符合形状定义的情况.为正确辨别所有不合形状定义的易变数据结构,本方案分别就5种简单形状提出了形状特征约束规则,若易变数据结构不符合约束规则,即可断定其属于待完善形状.根据关注点的不同,可将约束规则划分为3类:

1)关于节点在易变数据结构中所处位置对于节点类型的约束,如谓词节点仅可作为二叉树的叶子节点等;

2)关于节点主形状域入度的约束,用于判断绝大多数的异常指针指向关系,如单向链表中的环等;

3)关于节点间指针关系的约束,如用于描述双向链表和循环双向链表中相邻节点间指针的双向指向关系.

为简化各形状的表述,这里引入单向链表表段和双向链表表段,并在此基础上提供5种简单形状的谓词定义,如图9所示,其中p表示指向入口节点的指针,head和tail表示指向表头和表尾节点的指针.以上谓词定义均基于初始语义,确保从定义推出的任意两个有效指针都不相等.

根据形状的谓词定义,除入口节点即为NULL节点的情况之外,可以导出如下形状特征(入度指代主形状域入度,前向入度指代前向主形状域入度,后向入度指代后向主形状域入度):

1)单向链表表段(list_seg):所有节点均为结构节点或浓缩节点,除表头节点外,其余节点的入度为1;

2)双向链表表段(dlist_seg):所有节点均为结构节点或浓缩节点,相邻节点间的指针存在相互指向关系,且除表头和表尾节点外,其余节点的入度为2;

3)单向链表(list):在表段基础上,表头节点的入度为0,表尾节点的主形状域指向NULL节点;

4)循环单向链表(c_list):在表段基础上,表头节点的入度为1,表尾节点的主形状域指向表头节点;

5)双向链表(dlist):在表段基础上,表头节点的后向主形状域和表尾节点的前向主形状域均指向NULL节点,除非表头和表尾为同一节点,使其入度为0,否则它们的入度均为1,其中表头节点被后向主形状域指向,表尾节点被前向主形状域指向;

6)循环双向链表(c_dlist):在表段基础上,表头和表尾节点间存在指针的双向指向关系,且其入度均为2;

7)二叉树(tree):根节点的入度为0,其余节点的入度为1,且叶子节点为谓词节点或NULL节点,其余节点为结构节点或浓缩节点.

inductive list_seg(head,tail)= head=tail∪head≠tail∩ list_seg(head.forward,tail)inductive dlist_seg(head,tail)= head=tail∪head≠tail∩head.forward.backward =head∩dlist_seg(head.forward,tail)predicate list(p)= p=null∪∃q.list+seg(p,q)∩q.forward=nullpredicate c_list(p)= p=null∪∃q.list_seg(p,q)∩q.forward=ppredicate dlist(p)= p=null∪∃q.dlist_seg(p,q)∩q.forward= null∩p.backward=nullpredicate c_dlist(p)= p=null∪∃q.dlist_seg(p,q)∩q.forward= p∩p.backward=qinductive tree(p)= p=null∪tree(p.l)∩tree(p.r)

图9 形状的谓词定义
Fig.9 Predicate definition of shape

形状内分析的挑战在于需要处理的形状种类较多,不同形状拥有各自的形状特征,适宜的遍历方式亦不尽相同,为降低算法实现层面上的复杂度,形状内分析算法将算法分为两大部分:形状种类无关的遍历框架和位置相关的形状约束分析算法.如图10所示,算法首先通过GetNodeKind函数判断形状入口节点的类别,若为NULL节点(NODE_NULL),则直接通过形状内分析,因为所有形状类别的易变数据结构均可仅由一个NULL节点构成.之后,算法通过CheckHeadNode、CheckTailNode和CheckNormalNode函数进行位置相关的约束检查,它们是上述形状特征规则的实现,将节点的检查分为3种类型:对于链表形状,它们分别用于检查表头节点、表尾节点和其它节点,对于二叉树,CheckHeadNode用于检查根节点,CheckNormalNode用于检查其余节点,CheckTailNode没有意义,直接返回True,表示略过.算法的第10行至第16行为关于主结构节点的广度优先遍历,该循环的终止条件通过IsEnd函数实现判断,循环体每次从队首取出一个节点,使用CheckNormalNode进行检查,若通过则使用EnqueueNextNode函数根据形状类别获取相邻节点入队,对于链表,该相邻节点为前向主形状域指向的节点,对于二叉树则为当前节点的子节点,以此完成对于不同形状类别的主结构的统一遍历.

Input:Shape entry node E and shape kind TOutput:If the ADT can pass the analysis1 if GetNodeKind(E)==NODE_NULLthen2 return Ture;3 end if4 if CheckHeadNode(E.T)==Falsethen5 return False;6 end if7 Q←QueueCreate();8 EnqueueNextNode(Q,cur,T);9 cur←E;10 while IsEnd(cur,E,Q,T)==False do11 cur←Dequeue(Q);12 if CheckNormalNode(cur,T)==False then13 return False;14 end if15 EnqueueNextNode(Q,cur,T);16 end while17 if CheckTailNode(cur,E,T)==False then18 return False;19 end if20 return True;

图10 形状内分析算法
Fig.10 Algorithm of intra-shape analysis

算法通过IsEnd函数确定遍历是否终止,对于不同的形状种类,该函数的判断如下:对于二叉树,返回队列Q是否为空;对于单向链表或双向链表,返回前向主形状域指向的节点是否为NULL节点;对于循环单向链表或循环双向链表,返回前向主形状域指向的节点是否为入口节点.

4.3 形状推断

形状分析阶段预先判断了部分属于待完善形状的易变数据结构,对于通过形状分析的易变数据结构,形状推断会进一步分析非主形状域指针的指向,得到主结构和所有次结构的形状级别,并根据内置规则,实现易变数据结构所属形状级别的最终推断.如下给出3种形状级别的推断规则:

1)标准形状:仅存在1个非主形状域指向主结构的入口节点,不存在次结构,或者所有次结构均属于标准形状;

2)可接受形状:存在1个及以上的非主形状域指向主结构节点,仅存在声明节点域指向除入口节点以外的节点,不存在次结构,或者对于具有非主形状域指向的节点,其所指向的次结构属于标准形状或可接受形状,其余节点指向的次结构属于标准形状;

3)待完善形状:存在1个以上入口节点的易变数据结构,无法通过形状分析的易变数据结构,以及所有上述定义之外的易变数据结构.

形状推断规则指定,易变数据结构的形状级别由其主结构和所有次结构的形状级别共同决定.结合形状间分析阶段得到的结论,对于嵌套形状,各主结构通过嵌套形状域构成多叉树,也就是说,推断多叉树中某个节点的形状级别,即为对以该节点为根节点的子树的递归分析操作,分析起始于根节点,终止于形状级别已知的节点或不含次结构的易变数据结构,亦即叶子节点.形状间分析提前判定具环连通分量的形状级别,规避了递归分析算法不终止的情况.

1 Function DeduceShape(S,R) Input:Shape meta tuple S and shape level table R Output:Shape level2 if R[S]!=null then3 return R[S];4 end if5 L←ApplyRule(S);6 R[S]←L;7 if L==UNACCEPTABLE then8 return R[S];9 end if10 foreach s in GetSubStructure(S) do11 LS←DeduceShape(s);12 if L== STANDARD and LS== ACCEPTABLE then13 R[S]←ACCEPTABLE;14 L←ACCEPTABLE;15 end if16 if LS==UNACCEPTABLE or(L== ACCEPTABLE and LS==ACCEPTABLE and HasNonPrimaryPointInField(the node which points to s)==False)then17 R[S]←UNACCEPTABLE;18 break;19 end if20 end foreach21 return R[S];

图11 形状推断算法
Fig.11 Algorithm of shape deduction

在图11的算法中,首先通过第2行至第4行的分支语句判断结果表R中是否已经存在指定形状元信息S对应的形状级别,若存在则直接返回该结果.之后,通过ApplyRule函数推断S所对应的主结构的形状级别,如第7行至第9行所示,若主结构的形状级别就是待完善形状,则无需继续推断其次结构的形状级别,根据推断规则,无论次结构的形状级别为何,均不会改变该情况下主结构的形状级别.对于形状级别不为待完善形状的情况,则需要通过第10行至第20行所示的循环语句依次遍历其次结构,其中函数GetSubStructure用于根据特定形状元信息获取其次结构,循环体首先通过递归调用函数DeduceShape获取次结构的形状级别,然后结合次结构的形状级别实现对于最终形状级别的进一步修正,并将结果保存于结果表R之中,相关内容梳理如下,它们是推断规则的简化实现:若主结构为标准形状,且存在次结构为可接受形状,则需要将最终形状级别修改为可接受形状,实现如第12行至第15行的分支语句所示;若次结构为待完善形状或者主结构与次结构均为可接受形状,但指向该次结构的节点没有被非主形状域指向,则需要将最终形状级别修改为待完善形状,实现如第16行至第19行所示,其中HasNonPrimaryPointInField函数用于判断是否存在非主形状域指向目标节点.

5 实例验证

本研究在安全C语言验证器的形状系统中,实现了文中所述的形状检查方法.为检查文中算法和相关实现的正确性以及真实系统环境下的效率,我们设计了不同形状级别预期的易变数据结构实验用例,其组成如表1所示,按照由简至繁的顺序,这些用例可以分为:简单形状、嵌套形状以及复杂形状,其中复杂形状用例表示含有多个不通过嵌套形状域相连的易变数据结构的形状图,如图3所示.本实验通过上述用例确保其能够覆盖形状检查方法的各处理阶段以及其中的判定规则.

表1 实验用例组成
Table 1 Composition of experimental cases

形状级别简单形状嵌套形状复杂形状标准形状1042可接受形状1042待完善形状2482

实验在如下平台中进行:Windows 10 PC,Intel Core i7-6700 3.4GHz CPU和8GB DDR4内存,形状检查方法正确识别了所有用例的形状级别,结果如表2所示.

表2 实验结果
Table 2 Result of experiment

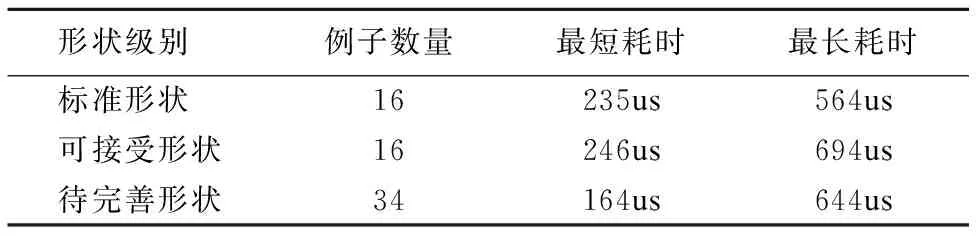
形状级别例子数量最短耗时最长耗时标准形状16235us564us可接受形状16246us694us待完善形状34164us644us

根据实验结果,不难发现在最短耗时场景下,待完善形状用例集的耗时最少,标准形状用例集次之,可接受形状用例集的最长.根据形状检查方法的设计,可以进行简要分析.属于标准形状和可接受形状的易变数据结构均需要经过3个阶段的完整检查方能得到最终形状级别,而嵌套形状域指向不符合定义的易变数据结构在最快情况下,于形状间分析阶段即可得到最终结论,使得后续阶段直接返回该结果,而无需进一步的处理,这使得该类用例的最短耗时少于其它用例,而在形状推断阶段才得到待完善形状结论,则是该类用例的最长耗时场景,这与可接受形状用例的最长耗时差别不大.导致标准形状用例集处理耗时少于可接受形状用例集的原因在于,无论易变数据结构是否含有嵌套形状域,在相同形状的前提下,属于标准形状的易变数据结构普遍比属于可接受形状的易变数据结构简单,具体体现在:其一,节点数量更少;其二,包含更少的形状域.这些区别主要影响形状分割以及形状内分析阶段的耗时.

此外,为衡量引入隐式形状检查后,对形状系统主要验证点蕴含操作的影响,我们还对当前系统的蕴含证明操作的耗时进行了采样,对于较为简单的易变数据结构而言,如单向链表,一次蕴含操作的平均耗时在30000us以上,该耗时取决于断言的复杂度以及Z3的证明效率,相较表2中的最长处理耗时而言,我们认为形状检查操作带来的时间开销几乎可以忽略不计.

6 相关工作

DRYAD[12]是分离逻辑[13]的一种方言,它提供了更加自然的方式描述堆块,并通过递归定义的方式描述易变数据结构,规避显式的量词使用,使得程序的自动化证明成为可能.该工作通过蕴含证明的方式完成对于易变数据结构的验证,本质上该方式将检查工作交由断言提供者完成,系统仅需要确保证明的正确性即可,可以保持系统的精简,且关于易变数据结构的检查亦更加自由,但也增加了断言描述的难度,对使用者要求更高,且检查仅在含有蕴含证明的大验证点进行,不利于及时发现易变数据结构中的问题.

文献[14]提出了针对命令式的数据结构的逐步精化验证方法,通过自顶向下的方式,将复杂数据结构拆分为算法思想与底层实现分别验证以简化证明过程,同时允许复用已验证的基本数据结构构造复杂数据结构,并将其作为算法验证的基础.该工作的亮点在于支持更加复杂的数据结构的证明,并通过相关工具实现使得模块化地构建经过证明的复杂数据结构成为可能.该工作使用分离逻辑处理堆内存的操作,需要使用者自行描述易变数据结构的定义,而系统则根据定义通过蕴含证明的方式完成数据结构的检查,对于使用者的要求较高,在复杂程序中同样难以及时发现问题.

PEDANTIC[15]是一款基于分离逻辑的可扩展交互式证明框架,基于Coq实现,能够用于验证含复杂动态数据结构操作的类C语言程序.该工作的特色在于其提供了一系列证明策略,尽可能实现断言正向演算的自动化,并在演算后简化断言的表述,针对易变数据结构,该工作的最大亮点在于其提出了跨结构不变式的概念,证明由不同类型的数据结构组成的复杂数据结构.与其它基于Coq实现的交互式证明框架一样,该框架同样无法彻底实现自动化证明,需要使用者手动证明部分定理,且对于易变数据结构是否符合定义的检查同样依赖蕴含证明,局限性和上述工作相同.

7 总 结

形状系统限制了程序中可以构造和使用的易变数据结构的种类,规避任意构造和操作易变数据结构给程序验证带来的困难,然而由于易变数据结构操作的特点,无法时刻确保其符合形状定义,为形状系统的演算带来了隐患.本工作提出了一种通过多阶段处理的方式检查易变数据结构是否符合形状定义的方法,它适用于含有易变数据结构操作的C程序的检查,能够支持单向链表、双向链表、循环单向链表、循环双向链表、二叉树以及这些数据结构的组合.分阶段检查的思想,简化了各阶段的关注点,从而降低相关检查算法与实现的复杂度.而提供显式形状检查和隐式形状检查,则免除使用者通过繁琐的断言描述程序状态,使得形状检查能够在任意程序点进行,更具灵活性和易用性.

形状检查方法同样存在一些局限性:第一,对于复杂数据结构的支持有限,例如B树、跳表等数据结构;第二,每次形状检查均需要完整地执行3个阶段的操作,在很多情况下是不必要的,例如在相邻显式形状检查之间的程序语句并不修改指针域,则此时两次检查得到的形状级别并不会改变.

针对形状检查方法存在的局限性,进一步的研究如下:第一,改进形状系统对于形状的表述方式,并增加相应的判定规则,使得系统整体可以验证和检查更多形状种类的易变数据结构;第二,研究形状检查的增量检查方法,在增量检查方法中,形状检查操作随程序语句的演算进行,在检查点仅需直接将实际的形状级别与预期的形状级别进行对比即可,可以规避无意义的操作,并且将检查的时间开销分摊.