一种运用模糊综合评判的实时服务器负载均衡算法

邰滢滢,薄 旭,庞 影,付云鹏

(辽宁大学 信息学院,沈阳 110036)

1 引 言

服务器的实时性是服务端对客户端的请求在指定时间做出响应的性能.实时性高的响应时间短,实时性低的响应时间长.对实时性没有严格要求而只要求处理任务的吞吐量的服务器是任务性服务端.传统意义上研究服务端负载平衡都是任务分配的负载平衡.随着大数据时代的到来,实时服务器负载平衡问题越来越突出.比如腾讯、微信等有上亿客户端,其后台服务器网络如何实时响应这些海量请求;再如随着自动化的发展,当远程开关数量猛增,它们所控制的后台服务如何支撑才能让开关控制延时不至于不可接受;还有金融交易、军事应用等,都要求配备实时服务器网络,它们都需要对用户的请求做出快速响应,也就是说都要求后台服务器的负载均衡.以上这些服务器有共同的特点:客户端巨大,必须由集群才能支撑;服务端对客户端的请求必须在指定时间内做出响应.基于这两个特点,有两种解决方案,第一是有一个硬件配置足够强大的后台服务器网络,实现服务器处理能力的提升,但是这种方式通常要增加一定量的硬件设施,构成更复杂的网络,不利于维护和管理;第二就是必须有一个好的均衡算法使得服务器快速响应,这种方式强调的是使用最小的资源成本,提高网络效率,最优化用户体验,所以一直是学者们关注的重点.

由于一般服务器处理客户端请求时都要消耗cpu,内存,带宽,占用硬盘读写io,按客户端请求的特点,可以分为:计算型请求,io型请求,网络型请求,内存型请求.目前的研究都是先判断请求的所消耗的主要资源,忽略其他次要资源.然后以这一主要资源做排序算法,选出最优服务器[1-3].即使考虑了其他资源也是作为参考或者辅助参量.这就忽略了系统资源的多参量性.尤其对实时性要求较强的场合,如:基于带宽为主要资源选出的最优服务器,因其次要资源cpu或内存短缺,很有可能不能实时响应客户端请求.所以系统资源的多参量性在实时服务器负载平衡中不可忽视.

而模糊综合评判算法本身能较好地解决模糊的、难以量化的问题,适合解决各种非确定性问题.尤其该方法曾经在农业选种上有过成功应用.农业选种问题与本文所提出的问题具有相似性.基于此,本文提出了一种基于模糊数学的评优方法,它综合了服务器的所有资源,进行多参量的评估,选出当前网络中最适合做出应答响应的服务器.

2 相关工作

针对网络集群的负载平衡问题,文献[1]提出了基于一致哈希算法的策略,由于哈希算法本身可以在概率上保证网络节点的流量平均分配,但是由于每个节点访问压力不同,所以对访问的处理时间是不一样的.因此创建了重载队列,根据阈值,如果确定是重载节点,会将此任务再分裂,将一部分数据分散到其他轻载节点,直到该队列为空.通过这样不断分裂式的调度,使得系统实现负载均衡.但是这种任务分片的阈值设置会影响整个系统的效率.文献[3]针对大规模网络集群,响应慢,服务质量不高的问题,提出了全局应用静态整体轮询的方法,把大集群分为几个相对较小的集群,在每个小集群内计算其负载熵,若负载熵小则认为该小集群出现了失衡,需要进行负载迁移,如果负载熵较大,那么认为该集群负载平衡.这样就避免了通信延迟.文献[4]提出了一种自适应的分布式负载均衡算法,它对网络中的服务器建立了路由表,根据路由表进行任务匹配,同时会计算各节点的负载信息,也就是LC的值,根据负载波动率更新LC的值,确定选择哪一个服务器副本.该方法需要不断维护和更新系统的路由表和LC测度表,但是当网络变化比较大时,路由的计算时间会比较长,也就是当网络处于一种过渡状态,极有可能会发生拥塞,而且路由协议也会影响网络的效率.文献[5] 提出了在全局负载均衡下云环境中的大数据动态迁移方法,这种方法首先构建了最小成本数据迁移模型.然后计算数据传输成本,评估虚拟机数据加载的利用率,把数据超载的服务器转移到数据轻载的服务器.这种方法在一定程度上,降低了数据迁移的成本,但是以计算步骤增加,网络开销增大为代价.文献[6]中提出基于流散列的负载平衡方案,主要是由于数据中心网络处理的各种作业负载,从延迟敏感的小流量到带宽需求高的大流量不等.处理步骤主要包括：i)在软件最底层接近硬件的软边缘实现网络负载平衡功能(例如虚拟交换机),这样传输层、客户虚拟机、或者网络硬件都不需要变化；ii)深层次的负载均衡,设计和实现一个边缘层软件的负载均衡方案,称为Presto,并在10 Gbps的物理实验平台做了评估.演示了分组重新排序对接收机的计算影响,并提出一种处理tcp接收分流功能中的重新排序的机制.该方法对硬件依赖较强,适合集中处理的数据中心模式,实时性稍差.文献[7]中主节点为所有基于Qos的文件过滤存储请求都设置了阈值,再计算每个存储节点的最高可用估计值,然后根据该值将任务分配给存储节点,存储节点能够根据连接节点的变化定时自适应反馈更新自身信息.该方法在一定程度上减小了系统的平均响应时间,但是主节点需要不断遍历各存储节点信息,增加了系统开销.文献[8]首先研究任务分类,将目前服务的类型分为几个簇,根据服务器得到的请求,将任务归类到相应的簇,在该场景中,每个服务器集群只处理一种特定类型的多媒体任务,并且每个客户端在不同的时间请求不同的多媒体服务.一般而言,这种场景可以被当作一个整数线性规划问题处理,从计算方面讲是可行的.力图通过一种有效的遗传算法的植入方案解决这个问题.但是遗传算法计算复杂,参数选择具有很大的不确定性,搜索速度有限.

3 模糊综合评判方法

3.1 基本概念

基于模糊数学发展而来的模糊综合评判方法,本质来说是利用了模糊数学的隶属度理论,把确定事物的各个条件从模糊的,难以量化,转变为可定量评价的量,再将这些量按一定规则综合,给出一个总体评价[9].这个评价结果由于体现了决定事物的各个条件,所以清晰可靠,系统性比较强[10].适合本文服务器多参量的综合衡量.

模糊综合评判的基本原理:设集合X,Y是非空的,任给一个从X到Y的模糊映射f,可诱导出一个从X到Y的模糊变换:

Tf:F(x)→F(y);A|→Tf(A)=A∘Rf

(1)

其中,Rf是由f诱导出的从X到Y的模糊关系[9].X是服务器多种资源的权重向量的取值集合.Y是集群中的服务器服务能力向量的取值集合.而针对某一时刻给定服务器多种资源的值,存在一个从资源权重向量到服务能力向量的映射.该原理给出了这个映射Rf的求解方法.

标准确定,只从影响事物的众多条件中选择一个来对其进行评价,称为单一评判;从部分或者所有的单一评价中获得对某个事物的整体评价,称为综合评判.综合评判本身是一个决策过程,类似将所有事物排队,从中选优的方法.综合评判的数学表达式为:B=AR.其中A为权重集,R为单因素评判矩阵,〈M〉为采用的算子.

以下分别说明表达式中各个量的计算方法.A是因素集上的一个模糊子集的向量表,在综合评判中通常称之为权重集.它表示根据服务器的具体应用,系统对各资源的需求比例.如流媒体对服务器在响应过程中对带宽要求较高,那么该项占用的比例就要大一些.R是由模糊映射诱导出的单因素评判集:

〈M〉的选择一般分为:主因素决定型,主因素突出型,加权平均模型.

选用的算子要根据实际情况而定,本文的应用在考虑多因素时修正值由主要因素决定,所以选主因素突出型比较适合.

3.2 执行步骤

1)为评判对象寻找因素集U={u1u2…un}.

影响评判对象的众多相关因素构成因素集.

2)给出评判集V={v1v2…vm}

评判集又被称为评语集.它是因素集中各因素实际出现的数量.

3)从因素集中选择一个,进行单因素评判

对单因素ui(i=1,2,…,n)作评价,确定ui对评语vj(j=1,2,…,m)的隶属度rij,得出ui的单因素评价模糊子集,表示如下:

f:U→F(V);

(2)

其中,0≤rij≤1,i=1,2,…,n;j=1,2,…,m.

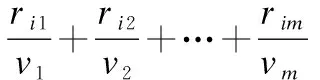
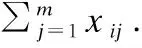
(3)

4)构造综合评价矩阵

根据模糊关系定理,由模糊值映射f导出U到V的模糊关系R,称矩阵R为综合评判矩阵.也就是把模糊隶属度rij作为矩阵元素,构成总评价矩阵Rf:

5)确定因素重要程度模糊集

因为影响事物的各因素其重要程度不一样,影响力也就不同,有些大,有些小.所以,在进行综合评判时,必须给出各个因素在总评价中的重要程度,用模糊子集A来表示:

A={a1a2…an}

其中ai表示ui的影响程度大小.这里称A为U上的因素重要程度模糊子集,而称ai为因素ui的重要程度系数,也称A为对应因素的权重向量[9].本文的权重计算方法将在下一小节中详细说明.

6)确定综合评判模型

当因素重要程度模糊集A和综合评判矩阵模糊关系R确定后,通过R做模糊线性变换,把A变为评判集V上的模糊子集[9],采用主因素突出型的计算形式为:

(4)

其中V是求最大值.

7)计算综合评判结果

对上述计算结果进行评价排序,即从U到V的模糊变换.将结果归一化,选择模糊隶属度最大的服务器作为该问题的最优解.也就是本次服务重定向的目标.

3.3 权重计算

重要程度模糊因素集A的确定十分重要,因为它直接关系到综合评判的结果是否正确.目前向量A的确定方法主要有几种:求解模糊关系方程法,专家调查法,Delphi法(专家评议法)等.本文主要通过Delphi法,研究其改进策略.

Delphi法是利用专家集体智慧来确定各因素在评判问题或者决策问题中的重要程度系数ai(i=1,2,…,n)[11].具体步骤如下:

1)确定各因素ai的重要性序列值

邀请专家们凭个人的经验和见解,评价各因素ui的重要性序列值ei,下面给出ei∈{1,2,…,m}的确定方法:对最具影响力的因素,取ei=m;对最不具影响力的因素,取ei=1.那么对于因素ui,第k个专家所得出的因素重要性序列值记为ei(k).每一位专家都提供一份这样的评定序列.

2)编制优先得分表

根据n次实验所的因素重要性序列值ei进行如下统计[11]:

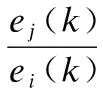
设实验共做了n次,将所有实验的Aij(k)值累加起来,即

(5)

由此得m*m个统计值.

3)求∑Ai值

将上式中的Aij值按j累加起来,令:

∑Amax=max{∑A1,∑A2,…,∑Am}

(6)

∑Amin=min{∑A1,∑A2,…,∑Am}

(7)

则与∑Amax相对应的因素的重要程度最高,而与∑Amin相对应的因素的重要程度同其他因素相比是最低的[11].

4)计算级差d[11]

令amax=1,amin=0.1,则:

(8)

5)求因素重要程度系数ai

ai可由公式(9)计算:

(9)

由此得出所需要的描述因素重要程度的权重向量:

A=(a1,a2,…,am)

实际上,综合评判研究对象因素集中各因素的量和对象本身优劣之间有一个函数关系.如果这个函数在应用范围内是接近线性的增函数,那么与其用专家评议法就不如实验评议得到的数据更能反映现状.原因是这种类型的综合评判研究的对象的因素集中各因素的相关量有如下特点:1)对象集各因素都是实测量,具有客观性,且各因素之间的相关性比较小;2)因素集各数据可以随时获取;3)因素集各数据在应用范围内是接近线性的增函数.据此,本文将专家评议改进为实验评议,它和Delphi法的主要差别在于输入的数据不再是每一位专家提供的一份各因素ui的ei值评定序列,而是实验测试的数据序列.这种方法适合客观性强并且实验数据能够随时再现的系统的权重向量A的确定.

4 实验及分析

4.1 权重计算

权重的数值是服务器响应具体应用请求所用各种资源的比例.它只和具体应用关系比较大,和服务器配置关系比较小.为了让权重向量计算结果准确,实验中采用实际流媒体娱乐服务项目中服务器的配置.使权重计算结果在本类应用中具有代表性.

本文中实验评议法输入的数据是在应用范围内的压力测试均匀采样.

1)搭建单服务器实验环境

原来有集群支撑的系统改为用单服务器.然后做模拟客户请求.由集群中取出一台电脑.处理器是intel i5-2300 2.8GHz,内存8G,硬盘西部数据1T,网络Realtek百兆网卡.

2)取得实验数据

a．测出服务器的最大负载量.同时瞬间向服务器发出模拟客户请求,当有请求失败时的请求数为服务器的最大负载量M=1098.

b.设置10个采样点.单次同时瞬间向服务器发出模拟客户请求数是M/n=1098/10=109.8.

10次同时瞬间向服务器发出模拟客户请求数分别是:109.8,219.6,329.4,439.2,549,658.8,768.6,878.4,988.2,1098.这些数据是从服务器无负载到满负载过程中的均匀采样,覆盖了服务器整个运行过程.

由10次实验得出一份各因素ui的ei值评定如表1所示.

表1 因素评定表
Table 1 Evaluation form of factors

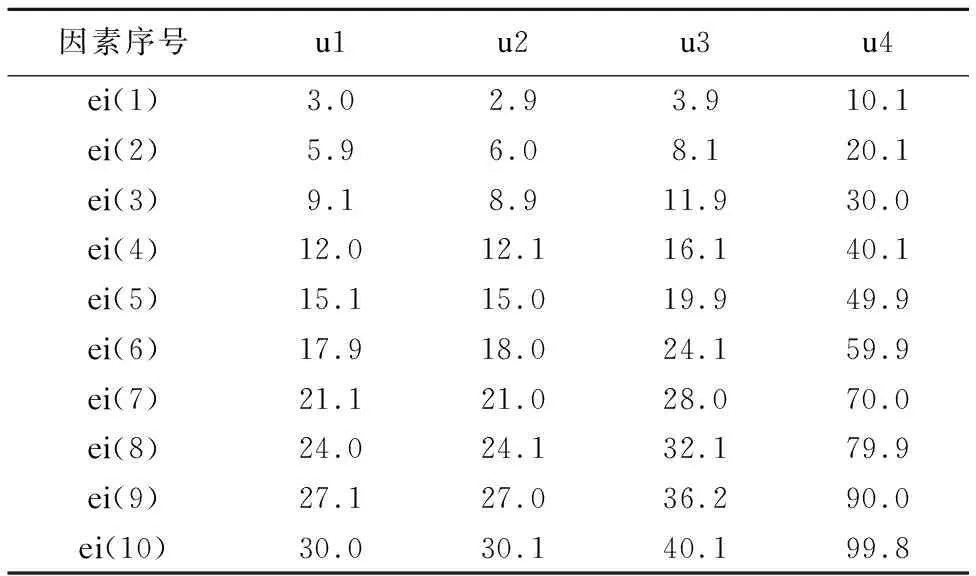
因素序号u1u2u3u4ei(1)3.02.93.910.1ei(2)5.96.08.120.1ei(3)9.18.911.930.0ei(4)12.012.116.140.1ei(5)15.115.019.949.9ei(6)17.918.024.159.9ei(7)21.121.028.070.0ei(8)24.024.132.179.9ei(9)27.127.036.290.0ei(10)30.030.140.199.8

3)编制优先得分表

根据10次实验所的因素重要性序列值ei进行统计,结果如表2所示.

表2 优先得分表
Table 2 Prior score

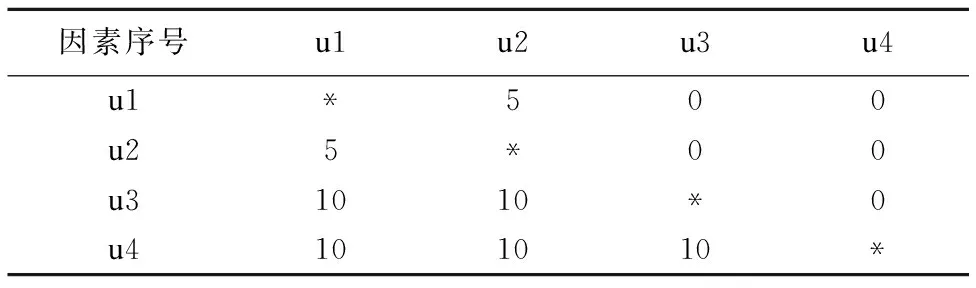
因素序号u1u2u3u4u1*500u25*00u31010*0u4101010*

4)求∑Ai的值

∑Amax=30,∑Amin=5

5)计算级差d

6)权重向量的系数ai

根据前述公式得出权重向量:A=(0.10.1 0.55 0.91).

4.2 准确性测试

本例集群由5台服务器组成,每台服务器参与评判的参量为CPU,I/O,内存,带宽,所以U={u1u2u3u4},设u1为服务器cpu剩余百分比,u2为服务器内存剩余百分比,u3为服务器硬盘io剩余百分比,u4为服务器网络带宽剩余百分比.这些参量是反应服务器的实时请求响应能力的主要指标.V={v1v2… v5},表示评判集.在某一时间点,对集群中的5台服务器的实时响应能力进行排序.因本例集群是流媒体服务器,主要考虑对流媒体服务请求的响应,由于流媒体服务对服务器的带宽和硬盘要求高一些,根据实验评议法测得的权重为:A=(0.1 0.1 0.55 0.91).

因为服务器集群在任何时刻都有可能有客户端请求.所以任何时刻集群对客户端请求都很重要.而在集群负荷高于70%低于%90最具代表性.因为低于70%总体负荷比较轻实时性容易达到.而高于%90系统已经接近满负荷,满负荷情况下无论怎样优化算法都不能对实时性有明显提高,只有增加服务器数量才能提高实时性.所以负载在满负荷的80%左右时,实验所用数据相对具有代表性.

对服务器集群进行压力测试,当达到权重实验的最大负载量的80%左右时,获取这一时刻集群中5个服务器4项剩余资源的取值,按上述步骤计算求解.

5个服务器的4项剩余资源指标如表3所示.

表3 因素评定表
Table 3 Remaining resource of servers

服务器编号x1x2x3x411.61110.590.691.6721.4299.440.161.5031.4475.970.241.2541.57210.750.751.7151.48310.990.751.44

1)单因素评判矩阵,如表4所示.

表4 因素评定表
Table 4 Judgement matrix of single factor

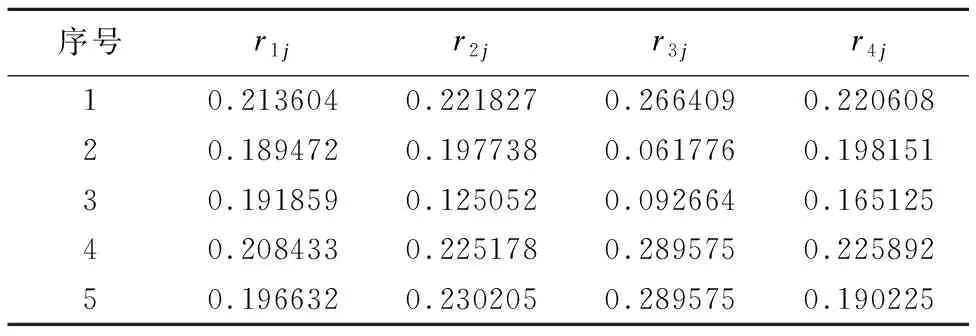
序号r1jr2jr3jr4j10.2136040.2218270.2664090.22060820.1894720.1977380.0617760.19815130.1918590.1250520.0926640.16512540.2084330.2251780.2895750.22589250.1966320.2302050.2895750.190225

2)综合评判

B=A∘Rf=(0.200753,0.180317,0.150264,0.205561,

0.173104).

按服务能力从大到小的次序排列,5个服务器服务能力降序排列:4,1,2,5,3.

4号服务器服务能力为0.205561.从计算结果看,它的服务能力最强,所以本次请求应分配给4号服务器.从资源指标表1可以看出,cpu剩余最多的是1号服务器,内存剩余最多的是5号服务器.4号服务器cpu和内存剩余虽然不是最多的,但这两项指标也是排名靠前.再看硬盘io和带宽剩余两个参数,4号服务器明显出众.而又由于流媒体的硬盘io和带宽权重占的比重大,所以4号服务器明显胜出.所以该算法所得结果明显合理.

4.3 时间代价测试

实验方法,搭建一个服务器集群,如图1所示,由五台电脑构成.处理器是intel i5-2300 2.8GHz,内存8G,硬盘西部数据1T,网络Realtek百兆网卡.运行两次压力测试,一次是硬盘io单因素算法,一次是模糊综合评判算法.在两次运行过程中,都在个别服务器上进行如下模拟压力测试:文件拷贝模拟硬盘io操作,压缩文件模拟cpu计算,申请内存测试程序模拟内存占用,下载文件模拟带宽占用.

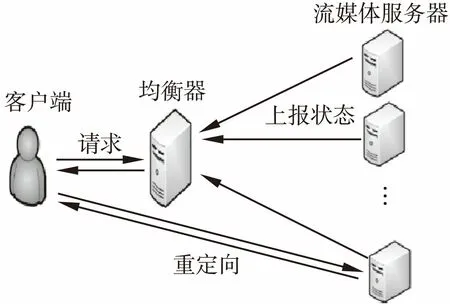
图1 服务器集群结构图Fig.1 Structure chart of server cluster

这个搭建好的服务器集群,分别配置成单因素算法和模糊综合评判时进行实验.对服务器集群进行压力测试,在模拟压力测试下,最大负载量80%时,获得20个平均返回时间的采样数据.绘制成图2.

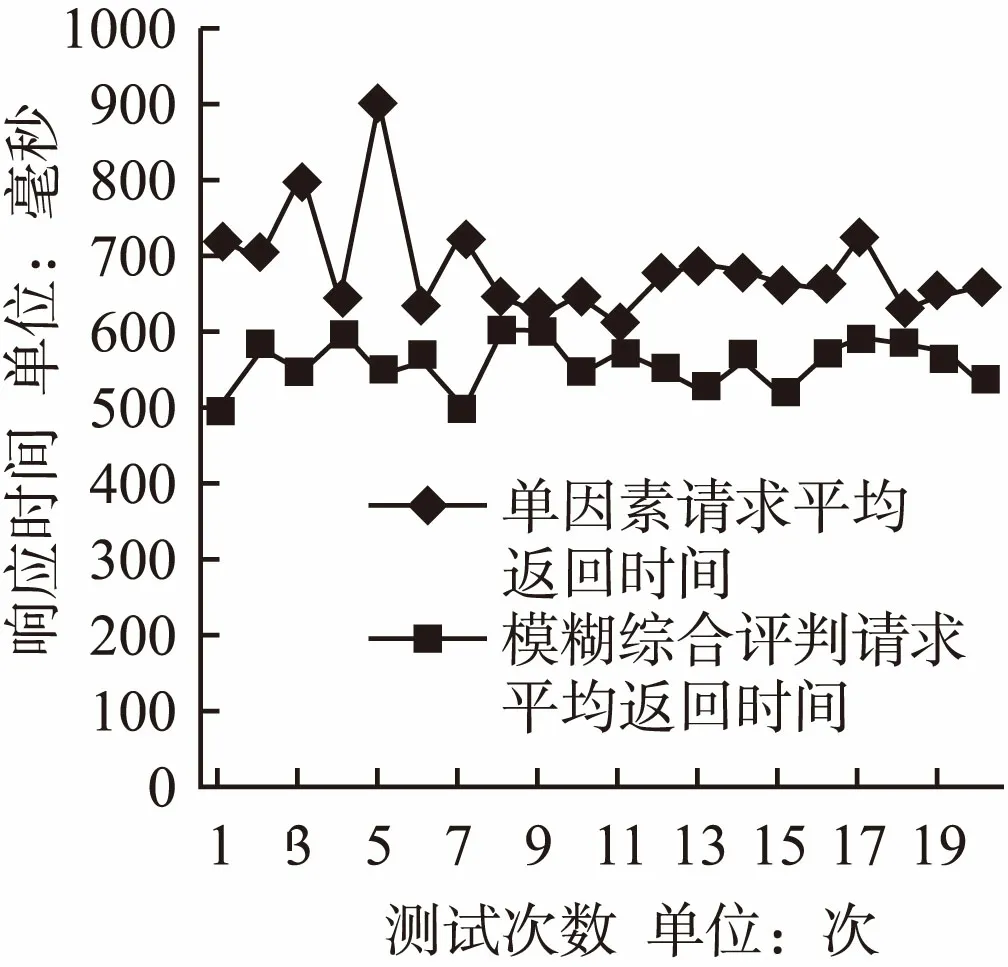
图2 两种算法时间对比图Fig.2 Time Comparison diagram of two algorithms

从图2可以看出,硬盘io单因素请求平均返回时间相对于模糊综合评判请求平均返回时间大部分都要长一些.其主要原因是,只有一小部分在硬盘压力测试时避开了有压力的服务器,而其余的cpu、内存、带宽这三个压力测试时,单因素算法并没有避开有压力的服务器,所以返回的时间明显较长.对于实时性服务器集群来说,实现实时性要求当客户端请求到来时,能够快速找到性能最优的服务器,做出迅速处理.虽然基于单因素的负载均衡算法也实现了实时响应,但是由于算法本身的限制,只能做到某一因素最优,而不能避开其他因素稍差的服务器,所以应答最快,但是处理时间未必最短,整体响应时间稍长,而新算法充分考虑所有因素的影响,不仅选出了最优服务器,成功地避开了整体性能有压力的服务器,而且使服务响应时间保持在一定的范围内,服务器集群的实时性得到了优化.所以本算法优于单因素算法,能够使服务器集群负载均衡,从而提高服务器集群的实时性.

5 结 论

随着大数据时代的到来,负载平衡问题已经成为实时服务器集群响应的重要问题.均衡算法的快速性和准确性直接影响着系统的性能.本文针对服务器系统的多参量性,提出了基于模糊综合评判的负载均衡算法,根据模糊数学理论,模糊综合评判能够对受到多种因素制约的事物或对象做出一个总体的评价的特点,对集群中服务器各参量,计算评判矩阵,利用主因素型公式,对所有参量进行综合评判,模糊隶属度最大的为当前任务重定向的目标.从实验结果来看,该算法可以在负载均衡问题上做出正确的决策且实时性比传统的基于单一参量的评判算法更优.