一种基于信任机制的概率矩阵分解协同过滤推荐算法

王建芳，苗艳玲，韩鹏飞，刘永利

(河南理工大学 计算机科学与技术学院，河南 焦作 454000)

1 引 言

推荐系统RS(Recommender Systems)为特定用户推荐其可能感兴趣的项目(例如书籍、新闻、美食和图片等).目前，推荐系统的研究方法主要是根据用户提供的反馈信息进行预测推荐[1].协同过滤CF(Collaborative Filtering)是该领域最常用的方法之一，核心思想是通过相似用户或相似项目的评分信息来预测用户偏好[2].协同过滤算法通常分为两类：1)基于内存的方法，主要包括基于用户的协同过滤和基于项目的协同过滤；2)基于模型的方法，主要是基于潜在因子模型，也称矩阵分解模型，其基本思想是通过训练集的训练以构建相关模型，然后使用该模型向用户推荐项目[3].

尽管基于潜在因子模型的推荐系统取得了较好效果，但在实际应用中仍遇到一些问题[4]，比如数据稀疏性和冷启动问题.由于用户有选择地对部分项目评分，导致用户项目评分矩阵数据稀疏，稀疏性使得模型很难从特征值中学习到用户偏好[5].有学者对社会科学中的同伴选择和社会影响进行深入研究[6，7]，发现用户往往与具有相似爱好的用户保持较紧密的联系，信任关系恰恰能反映用户之间的紧密程度，能进一步增强同一社交圈成员的相似性.近年来利用用户之间的信任度提出的相关推荐算法，虽然提高了推荐质量和覆盖率，但是却是以牺牲精确度为代价的，而且由于社交网络中的信任稀疏难获取，造成推荐精度不高.

基于此，本文提出了一种基于信任机制的概率矩阵分解协同过滤推荐算法TM-PMF (Probabilistic Matrix Factorization Algorithm of Collaborative Filtering Based on Trust Mechanism)，该方法根据每个用户在信任网络中的节点信息，计算其信任值，从而构建用户的信任网络，最后基于用户评分矩阵和信任矩阵建立提出的TM-PMF算法模型.

2 相关工作

传统的矩阵分解模型有奇异值分解SVD(Sigular Value Decomposition)、概率矩阵分解PMF(Probabilistic Matrix Factorization)和非负矩阵分解模型NMF(Non-negative Matrix Factorization)等.文献[8]提出了概率矩阵分解模型，该模型从概率生成过程角度描述矩阵分解过程，有效缓解了数据稀疏性问题；文献[9]提出了基于邻域相似性的矩阵分解模型，该模型考虑了用户兴趣相似度，进一步挖掘评分矩阵的有效信息，提高推荐精度.近年来，随着使用社交平台和社交网络的用户数量增多，依赖性增强，社交信息为协同过滤算法带来了新的数据源[10]，如好友推荐和信任用户推荐均有效促进了用户的消费行为，因为在现实生活中相对于品牌、价格和销量等参考标准，用户更倾向于信任好友的推荐.文献[11]显示相对于系统给出的推荐，人们更喜欢来自友人的推荐，在线调查结果还显示，76%的人们对其友人的在线评论：可信(13%)和有点可信(63%).鉴于此，大量研究人员开始运用社交信息来改进推荐算法.

文献[12]给出了信任在推荐系统中的定义，即一个用户对另一个用户提供有价值评分的信赖程度.文献[13]提出将社会信任融入推荐算法，来缓解数据稀疏性问题.文献[14]提出基于用户之间的距离对其信任值进行度量，根据信任关系进行评分预测.文献[15]将社交信任信息融合到基于模型的协同过滤算法中.文献[16]则提出了基于信任传播的概率矩阵分解，该方法将信任传播机制与PMF算法融合，使用直连信任用户和间接信任用户的信息进行推荐.但是该方法存在不足，其使用信任网络预测用户的潜在特征向量，然后联合项目潜在特征向量进行评分预测，使得该算法的结构计算复杂度较高，而且该算法使用的信任矩阵是二值矩阵，信任值只有0或1，忽略了用户对于不同信任用户的信任度是有差别的.

由此可见，基于信任的推荐算法能够有效地缓解冷启动和数据稀疏问题，但是其本身也存在缺点，如何更好地计算信任值，并将其融入推荐算法是接下来本文所研究的重点.

3 问题定义

在推荐系统中包含有一组N个用户的用户集U={u1，u2…uN}和M个项目集合I={i1，i2…iM}，用户对项目的评分数据用矩阵R=[Ru，i]N×M表示，Ru，i表示用户u对项目i的评分，评分值一般是[1，5]中整数，数值越大表示用户越喜欢该项目.本文在不失一般性的基础上，通过归一化方法将评分1-5映射到[0，1]范围内.

在评分网络中，每个用户u有一组直接邻居用户集Nu，通常用户之间的信任矩阵是一个二值矩阵T=[Tu，v]N×N，tu，v表示用户u对用户v的信任值，0表示不信任，1表示信任.

4 概率矩阵分解模型

(1)

其中N(x|μ，σ2)表示x服从均值为μ，方差为σ2的高斯分布；Ii，j是指示函数，Ii，j等于1说明用户i已对项目j评分，否则为0；假设用户和项目的特征向量矩阵都服从均值为0的高斯分布，如式(2)所示.

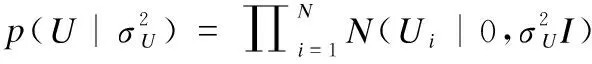
(2)

由贝叶斯公式推导可知用户和项目特征向量的后验分布，如式(3)所示.

(3)

经过推导并进行整理得到最终的目标函数，如式(4)所示.

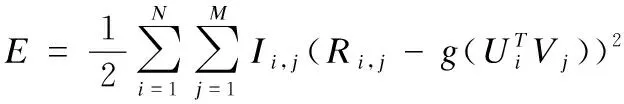
(4)

5 TM-PMF算法

基于信任的推荐算法可以有效地缓解冷启动和数据稀疏问题，如何更好地计算信任值，并将其融入推荐算法是研究的重点.本文提出的TM-PMF算法框架如图1所示.

图1 TM-PMF算法框架图Fig.1 Algorithm framework of TM-PMF

5.1 信任值计算

社交网站上的信任信息，大部分是采用二值型的：信任与不信任，但是二值型的信任数值所表示的信息量不足，无法体现用户对其信任用户集中用户的区别.例如：假设用户U1的信任用户集Tu包含四个用户U2、U3、U4和U5，即Tu={U2，U3，U4，U5}，显然在二值信任矩阵中用户U1对四个用户(U2，U3，U4，U5)的信任值相等均为1，然而现实生活中却不一定，有可能用户U1更加信任用户U3，因此根据信任网络数据，选择一种计算方法，使得用户U1对(U2，U3，U4，U5)的信任可以通过一个数值加以区分.如图2(a)所示为信任网络图，每个用户是图中一个节点，用户之间的信任值用图中的边来表示，一个简单的信任网络图和信任矩阵如图2所示.

对于U1来说，其入度(Indegree)为1，出度(Outdegree)为2，因此有用户i对用户j的信任值的计算方法如式(5).

(5)

其中Ti是指用户i的直连信任用户集合，例如：由图2可知用户U1的信任用户集合Ti={U3，U4}，用户U3的入度是2，用户U4的入度是2，所以Trust(U1，U3)=√(2/(2+2))=0.707，根据此方法重新构造信任网络，且信任值的取值范围为[0，1].但该方法的不足之处是如用户U5的直连信任用户只有U4，其信任值就为1，这与实际情况不符.因为即使用户U5只有一个信任用户U4，U5对U4也不可能100%信任，对于U4的推荐也不可能完全接受.

(a) 用户之间信任网络图 (b) 用户之间的二值信任矩阵

图2 用户之间的信任机制关系图
Fig.2 Trust mechanism of users

同时由Massa和Avesani提出了基于距离的信任值计算，该方法虽然复杂度较低，但是遗漏了很多可用信息，造成信任的缺失.基于此，本文信任值的计算方法如公式(6)所示.

(6)

该方法根据用户在信任网络中的节点位置，从用户角度出发，既考虑用户被其他用户信任的次数(入度)，又考虑了用户信任别人的次数(出度)，而每个用户的出度和入度信息在一定程度上反映了该用户在社交网络中的价值，可见，该方法能够较好地利用用户之间的信任关系，避免了基于距离的信任值计算方法常面临的问题：只要两个用户之间的最短距离相等则他们的信任值相等，其信任值的取值范围是[0，1].

5.2 TM-PMF算法

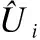
(7)

将式(7)展开成矩阵相乘形式可知，其实是将信任值作为权重加在对应的直接用户的潜在特征向量上，具体形式如式(8)所示.

(8)

实际评分与预测评分的误差所服从的概率分布如式(9)所示.

(9)

(10)

所以融合信任信息后的用户的潜在特征向量的概率分布如式(11)所示.

(11)

结合评分矩阵和信任矩阵的潜在特征向量的后验概率为：

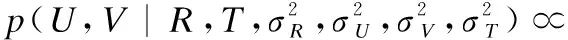
(12)

则对(12)取对数，得到的目标函数形式如式(13)所示.

(13)

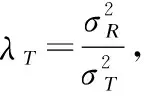
(14)

(15)

5.3 算法流程

输入：用户之间的信任矩阵TNN，用户项目评分矩阵RNM，用户潜在特征矩阵UNK，项目潜在特征矩阵VMK，算法最大迭代次数maxepoch，正则化系数λ，信任项的系数λT，学习速率α，读入数据的总批次numbatches，以及每批次读入数据的数量N.

输出：用户潜在特征矩阵U和项目潜在特征矩阵V，真实评分与预测评分的误差E，以及随着迭代次数变化的RMSE.

算法流程：

步骤1.读入评分矩阵RNM并处理，取任意75%的数据作为训练集，剩下的25%作为测试集，用来验证训练好的模型的鲁棒性；

步骤2.读入信任矩阵TNN，按照5.1提出的信任值计算公式(6)，计算用户之间的信任值，重新构建信任矩阵TNN；

步骤3.使用正态分布初始化用户和项目潜在特征矩阵UNK和VMK，for循环分批读入作为训练集的评分数据，将每个用户Ui的信任用户特征向量与其信任值加权存储；

步骤4.根据公式(13)，计算目标函数E，然后根据公式(14)和公式(15)，通过批量梯度法更新变量和训练参数：

for 迭代次数=1：maxepoch

for 读入评分数据批次=1：numbatches

归一化评分数据；

计算预测评分数据；

根据公式(13)计算目标函数E；

根据公式(14) 公式(15)计算变量的偏导数；

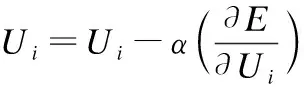
end

计算训练数据的均方根误差RMSE；

读入作为测试集的评分数据，利用训练集已经训练好的Ui和Vj，计算测试数据的均方根误差RMSE；

end

步骤5.根据每次选择的学习速率、正则化系数和矩阵分解的维度K，将RMSE随着迭代次数变化的曲线绘制出来，再根据曲线调整以上参数值，直到RMSE达到最优值，从而获取推荐列表.

算法结束.

6 实验分析

实验假设：1)不同用户对同一项目有不同的偏好，且同一用户对不同项目有不同的偏好；2)用户会受其信任用户的影响，从而更加偏向于信任用户的推荐，即如果用户U1越信任用户U2，则这两者的行为相似度越高.

不失一般性，为了减小算法复杂度，统一设置正则化系数λU=λV=0.001.

6.1 数据集

为了验证本文提出算法的推荐效果，选择了3个经典的包含信任关系的数据集，分别是Filmtrust[17]数据集、Epinions数据集和Ciao数据集.3个数据集详细信息如表1所示.

6.2 评估标准

为验证本文所提出算法的推荐质量，采用均方根误差RMSE(Root Mean Square Error)作为度量标准，这是针对评分预测方向常用的推荐质量度量标准之一，RMSE的定义如式(16)所示.

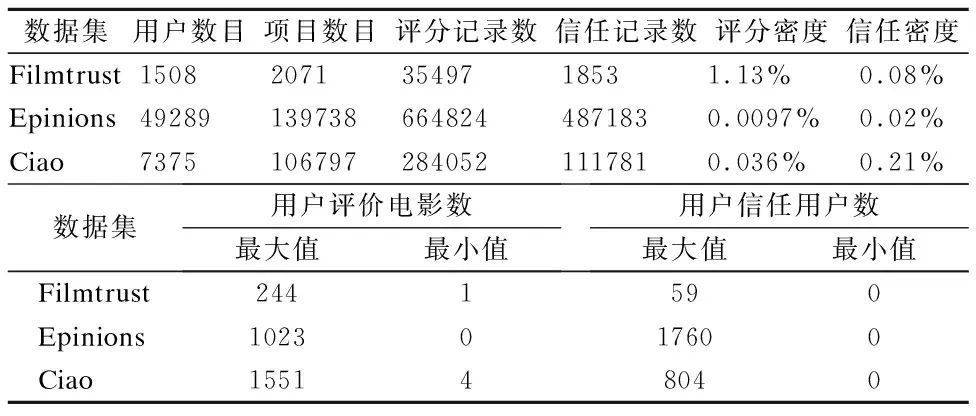
表1 3个不同数据集的统计信息表Table 1 General statistics of the Filmtrust， Epinions，and Ciao datasets

(16)

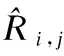
6.3 对比算法

为验证本文所提算法的有效性，检验信任因子对于推荐效果的影响，本部分实验分为两个部分，第一部分是对比PMF算法和TM-PMF算法的效果；第二部分是分析参数λT对推荐质量的影响.

1)PMF算法与TM-PMF算法

为了验证信任因子对推荐质量的影响，绘制了PMF算法和TM-PMF算法对应的RMSE曲线变化图.如图3、图4和图5所示.

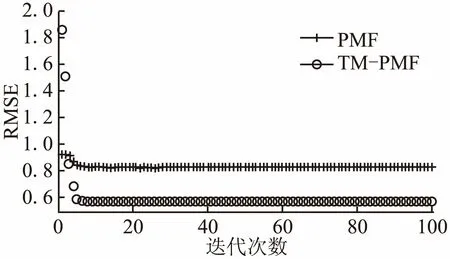
图3 Filmtrust数据集上RMSE 随迭代次数的变化Fig.3 Performance of PMF and TM-PMF in the Filmtrust dataset for RMSE

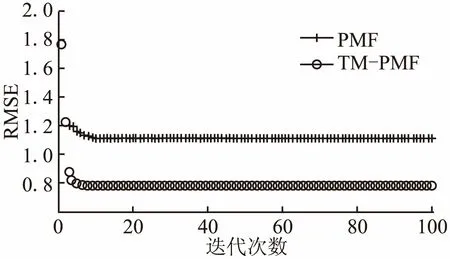
图4 Epinions数据集上RMSE 随迭代次数的变化Fig.4 Performance of PMF and TM-PMF in the Epinions dataset for RMSE

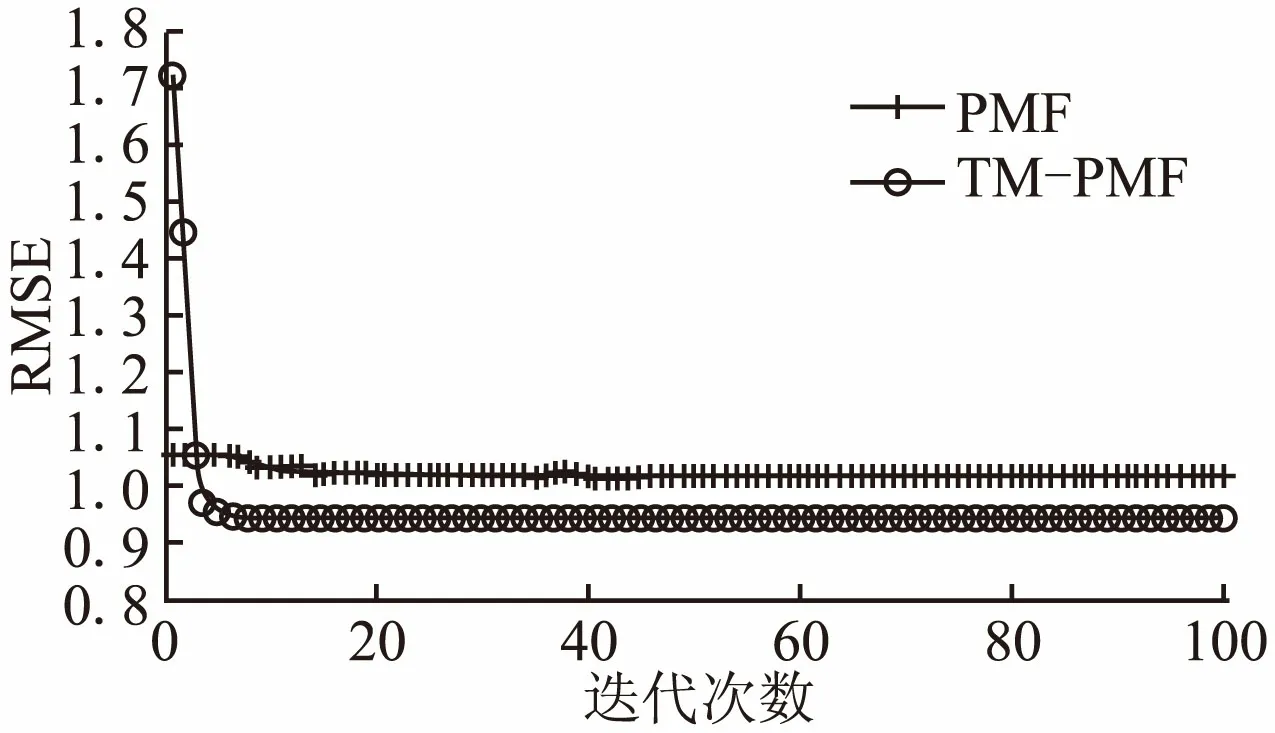
图5 Ciao数据集上RMSE 随迭代次数的变化Fig.5 Performance of PMF and TM-PMF in the Ciao dataset for RMSE

一般来说，RMSE的值越小推荐质量越好，可以看出，在不同数据集上加入信任因子的算法TM-PMF较PMF算法的推荐效果有明显提升.具体分析，在Filmtrust数据集上，如图3所示，当迭代次数小于3次，PMF算法和TM-PMF算法随着迭代次数增加，RMSE值迅速下降，PMF算法对应的RMSE值小于TM-PMF算法的，说明这种情况下PMF算法的推荐效果较好，当迭代次数大于3次，TM-PMF算法的推荐效果开始优于PMF算法，RMSE值仍然迅速下降，而PMF算法对应的RMSE值下降速度减缓；当迭代次数增加到10之后，两种算法均开始趋于稳定，迭代增加到20次以后，RMSE值基本不变；类似在Epinions数据集和Ciao数据集上，两种算法的RMSE曲线的收敛趋势大致相同，但是在Epinions数据集上TM-PMF算法的推荐效果更明显.根据表1所示，Filmtrust数据集的评分密度是1.13%，Epinions数据集的评分密度是0.0097%，Ciao数据集的评分密度是0.036%，结合上图对比结果可知，信任因子的加入对于稀疏数据集的推荐质量影响更大.

2)参数λT的确定

参数λT控制信任因子对用户行为的影响，λT的值越大代表信任因子对用户的影响越大，越小说明我们的模型越接近概率矩阵分解模型；当然λT的值并不是越大越好，λT的值特别大时，将会导致过拟合现象，即特征向量逼近训练阶段RMSE值较低的近邻用户的特征向量模型.

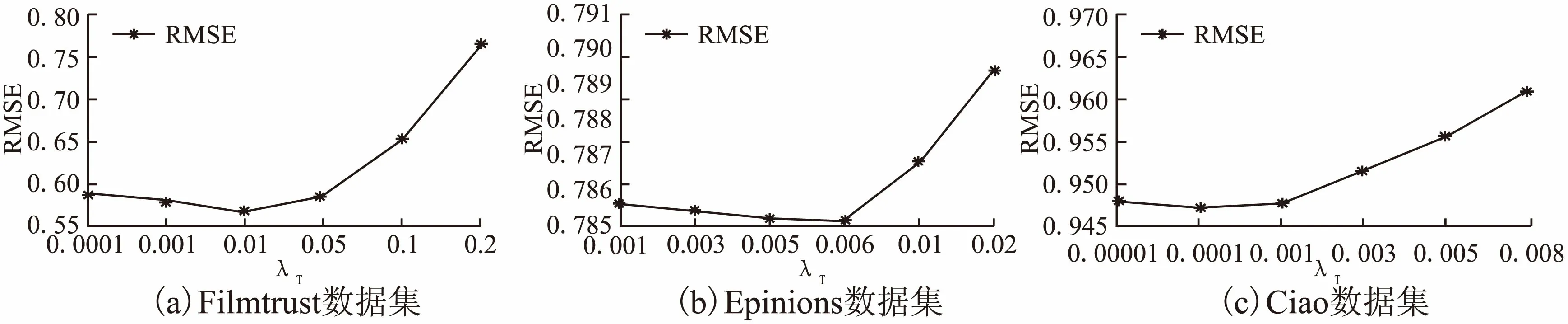
图6 不同数据集上参数λT对推荐效果的影响Fig.6 Impact of different values of λT on the performance of prediction in datasets

图6描述了在不同数据集上不同的λT对RMSE值的影响.具体在Filmtrust数据集上，当λT=0.01时，TM-PMF的推荐效果较好；在Epinions数据集上，λT=0.006；在Ciao数据集上，λT=0.0001.

7 结束语

本文提出了一种新颖的TM-PMF算法，该算法融合了用户的历史记录信息和用户之间的信任关系，更加真实客观地为用户推荐自己喜好的物品.实验结果表明本文提出的TM-PMF算法，在3个数据稀疏的数据集上的推荐结果精度均有所提高.接下来将结合动态数据流进一步改进本文提出的算法.