一种用于燃料电池含水量诊断的新型压力降模型＊

单希壮 杨月华 马天才 杨彦博 林维康

（同济大学，上海 201804）

主题词：燃料电池 水管理 故障诊断 压力降

1 前言

质子交换膜燃料电池（Proton Exchange Membrane Fuel Cell，PEMFC）因具有零排放和能量转化效率高等优点而受到广泛的关注和研究，但成本与耐久性问题阻碍着燃料电池的商业化应用。此外，含水量的控制也是制约PEMFC商业化的主要障碍之一。燃料电池内部含水量过多会降低能量转化效率，甚至造成催化剂腐蚀，缩短燃料电池的寿命。另外，在低温环境下停机时，内部形成的冰晶不仅会加大燃料电池的启动难度，还可能刺穿质子交换膜或压碎石墨板。而燃料电池含水量不足会增大其欧姆阻抗，降低能量转换效率，还可能造成质子交换膜的破裂或膜电极（Membrane Electrode As⁃sembly，MEA）的分层等结构性损伤。因此，含水量诊断技术成为燃料电池应用领域的研究重点和热点。

目前，用于含水量诊断的特征参数主要有：反应气体的进、排气压力降及其衍生量（简称压力降）[1-2]，如直接压力降[3-4]、压力降偏差值[5-7]和两相压力降系数[8]等；电化学阻抗信息[9-10]，如高频阻抗[11-13]等。基于压力降的含水量诊断方法成本低廉且数据来源广泛，因此获得了广泛的应用并取得了较好的成果。

压力降作为诊断参数需要准确的基准压力降作为比较对象。Steiner N Y[6-7]利用神经网络进行正常工作条件下的气体压力降建模。神经网络具有较高的模型精度，但是原始数据需求量大。裴普成[14]基于伯努利方程建立了理想化的单相流压力降模型，但该模型需要较多的燃料电池自身参数，模型精度有待提高。See E J团队[15-17]致力于燃料电池两相流模型的研究，但是目前两相流模型存在可描述的工况范围过窄的局限性。

为提高燃料电池含水量诊断过程中基准压力降的准确度，本文提出了一种燃料电池阳极压力降模型，并规定以水汽饱和状态下的单相流压力降运算结果作为基准压力降。该模型优化了氢气-水蒸气混合气体的粘度计算，提高了模型的精度，实现了气体流量与输出电流的解耦，使得基于压力降的含水量诊断方法在燃料电池系统启、停机吹扫等过程也可以得到应用。

2 模型构建

通常，燃料电池阳极流道中气体流速小于10 m/s，声速以340 m/s计，可得马赫数不到0.03，远小于0.3，因此压力降计算过程中气体可作为不可压缩流体。压力降来源包括氢气的消耗、沿流道方向的沿程阻力、局部阻力、重力压头和动压头。沿程阻力与流程长度和摩擦系数正相关。局部阻力指流体流经蛇形流道拐角处由于流体变形、方向变化、速度重新分布，质点间进行剧烈动量交换产生的阻力。重力压头由气体高度变化引起，动压头由截面变化导致的气体速度和压力的变化引起。燃料电池流道内重力压头与加速度压降通常不考虑，而单相流情况下局部压力损失远小于沿程压力损失，因此本文仅对沿程阻力和氢气消耗产生的压损进行建模。

2.1 模型假设

a.根据对基准压力降的规定，假设流道内处于水汽饱和的热平衡状态；

b.气体在进、出口和流道内的温度恒定且相等；

c.燃料电池电流密度均匀；

d.阳极侧液态水含量很低或气体流速较高时，流道截面积与水力直径沿整个流道长度的值近似相等。

2.2 雷诺系数

雷诺系数的表达式为：

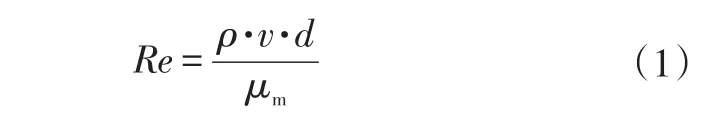
式中，ρ为气体密度；v为气体速度；d为水力直径；μm为混合气体粘度。

氢气摩尔流量为：

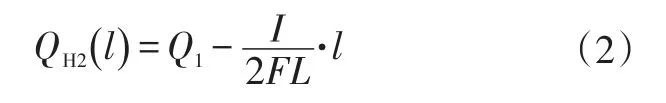
式中，Q1为氢气入口流量；I为电流；L为流道长度；l为沿程长度，0≤l≤L。

对0～100℃内水的饱和蒸气压进行拟合可得：

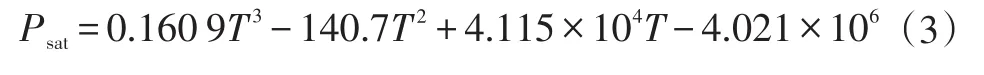
式中，T为温度；Psat为水的饱和蒸气压。

压力降的方法主要用于判定燃料电池的水淹故障，且燃料电池系统中带有氢气循环泵或氢气引射器，因此将水汽饱和状态下的压力降设定为压力降基准，即模型构建过程中阳极侧相对湿度恒定为100%。在此前提下，混合气体中氢气的分压为：

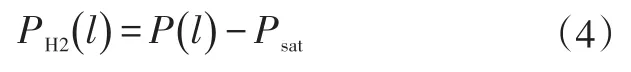
式中，P(l)为燃料电池阳极流道中的压力。

由于本文模型的目的是建立阳极侧气体相对湿度恒定为100%这一假定条件下的压力降基准，因此不考虑水的净迁移系数，即不考虑生成水对流道内气体性质的影响，这种处理方式在前人的研究中也较为常见。基于上述条件，水蒸气的流量等于氢气的加湿流量：

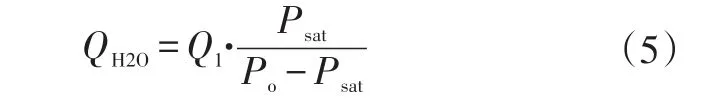
式中，Po为燃料电池阳极入口压力。

由此可推算混合气体的体积流量、质量流量和密度：

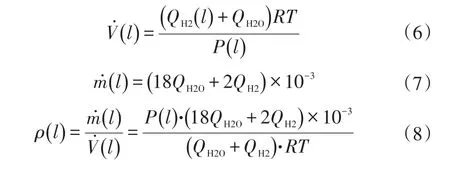
混合气体平均速度为：

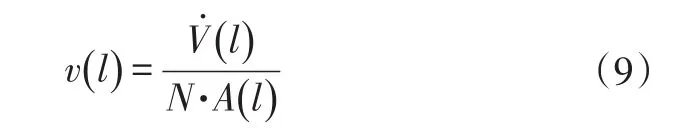
式中，R为气体常数，通常取8.314；N为流道数量；A(l)为流道的截面直径。

将式（2）～式（9）代入式（1）推出雷诺系数表达式：

由上述推导可知，在流道入口处雷诺系数最高。假设燃料电池阳极流道横截面为矩形，宽与深均为1 mm，流态为水汽饱和的单相流状态，化学计量比为10（实际操作中一般不大于此值），以文献[14]的粘度计算方法推算出雷诺系数如图1与图2所示。

图1 不同条件下的雷诺系数（120 kPa）

雷诺系数的运算结果远小于下临界雷诺系数2 320，因此可以得出结论：在本文模型的适用范围内，气体在燃料电池阳极侧始终处于层流状态。

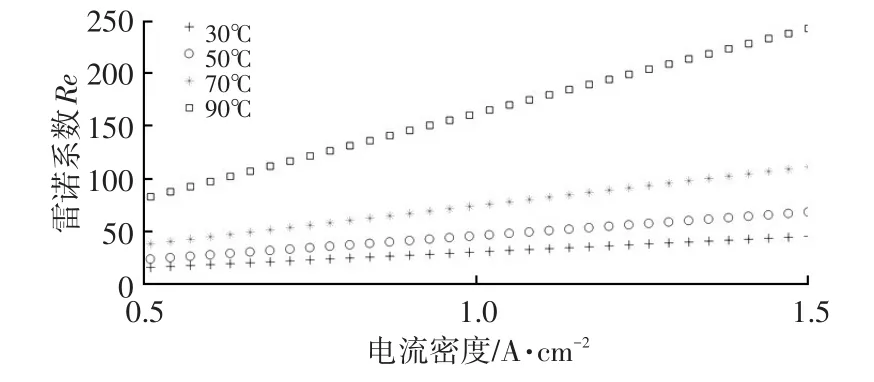
图2 不同条件下的雷诺系数（180 kPa）

2.3 饱和湿氢气粘度优化

对于本文的故障诊断模型，考虑水汽饱和状态下的氢/水混合气体的粘度。文献[14]直接给出了氢与饱和水蒸气混合气体的粘度公式：

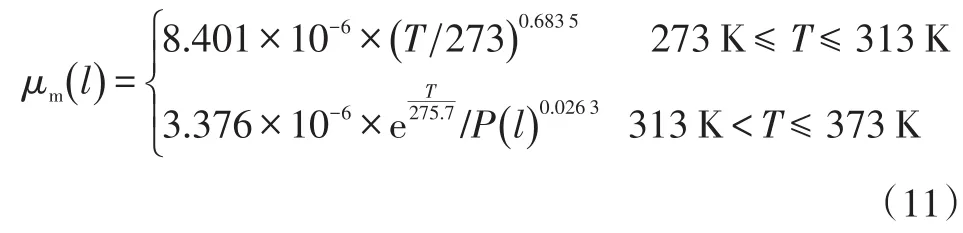
此外，还有其他较为重要的混合气体粘度计算模型。对于非理想气体混合物，混合物粘度可以根据各单质气体的质量分数计算：

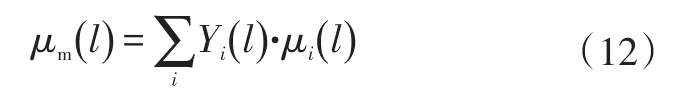
式中，Yi为组分i的质量分数；μi为单质组分i沿流程长度的粘度。

而利用理想气体定律，混合气体粘度计算公式为：

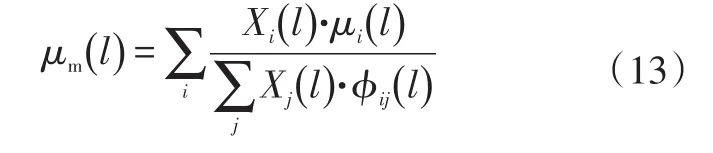
式中，φij(l)为混合物粘度结合因子；Xi为组分i的摩尔分数。

最常见的粘度结合因子计算方式由C.R.Wilke根据Sutherland的动力理论模型得出：

该公式接受度较广，比如常见的商业化流体计算与仿真软件Fluent便采用这一公式。但是，该公式应用于某些混合物体系，如分子量较小的轻物质与分子量较大的重物质组成的混合物体系，或强极性气体与其他气体组成的混合物体系时，计算结果与试验结果存在较大误差。本文所构建模型中氢气属于轻物质，水蒸气属于强极性物质，因此粘度计算过程中不可直接应用这一被广泛接受的粘度结合因子计算方式。

针对上述问题，童景山[18]对Sutherland提出的气体混合物粘度方程中的粘度结合因子进行了较大改进。

所述结合因子φij(l)的计算方法为：

式中，εij为无因次系数；Mi为组分i的分子量；Mij为算数平均分子量，Mˉij为几何平均分子量；Si为组分i的Sutherland常数；Sij为相互作用Sutherland常数，氢、氘、氦、氖气取79，水蒸气取961；Cs为极性因子，对一般气体取1，对于含强极性气体，如氨、水蒸气等体系，取0.733。

该方法特别适用于含氢气混合物体系。氢气单质的粘度计算公式为：

式中，g为重力加速度。

本文中，氢气粘度采用式（18）计算，水蒸气粘度采用式（20）计算。

上述4种混合物粘度计算模型得出的饱和湿氢气粘度和纯水蒸气、纯氢气粘度的对比如图3所示。理想气体定律下，根据C.R.Wilke结合因子的计算结果与其他3种混合物粘度结果相差较大，原因可参考文献[19]及相关著作。童景山改进的混合气体粘度计算模型与非理想气体混合模型的计算结果相对较为相近，尤其在低于35℃和高于90℃的温度范围内。然而，燃料电池的工作温度通常在30～80℃，为提高模型精确度，本文采用童景山的混合物粘度计算方法对以往文献中燃料电池模型的湿氢气粘度公式进行优化。

图3 4种混合物粘度计算公式对比

2.4 沿程压力降

根据达西公式，水头损失为：

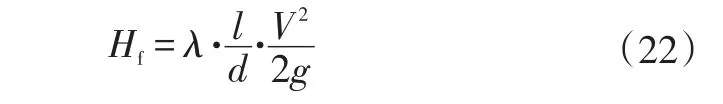
式中，λ为沿程损失因数，大小取决于雷诺系数。

对于燃料电池流道：

因此，在忽略重力压损与加速度压损的条件下，燃料电池沿流道方向的压力降为：

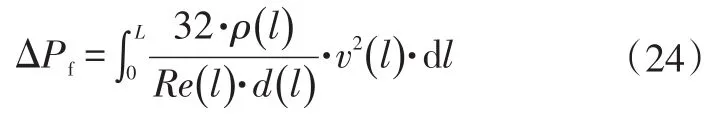
整合上述公式可得：

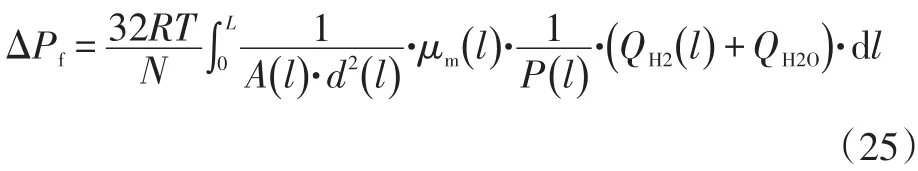
式（25）中，积分号内第1项代表流道属性，第2项为流体的粘度特性，第3项为流道内的压力特性，第4项为混合气体的流量特性。

对于单相流，第1项变量为常数，如果发生水淹，第1项的值将会沿流道方向快速增大，成为压力降升高的主要原因。根据2.1节的假设d，在单相流和轻度润湿的情况下，第1项变量作为常数被移到积分号之外。对于第2项，仅计算式（11）表明粘度与压强有关。本文采用童景山的方法进行混合物粘度的优化，粘度系数与压力无关，根据2.1节的假设a，无论低压或高压燃料电池系统，粘度变量可以视为常量移到积分号之外。对于第3项，由于燃料电池单相流压力降与燃料电池进气压力的比值极小，也可视为常量移到积分号之外。

因此，上述模型可以简化为：

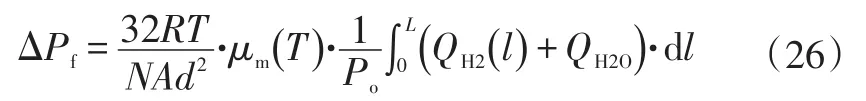
对积分号进行积分后，以待定系数替代模型中的常数项，最终计算结果为：

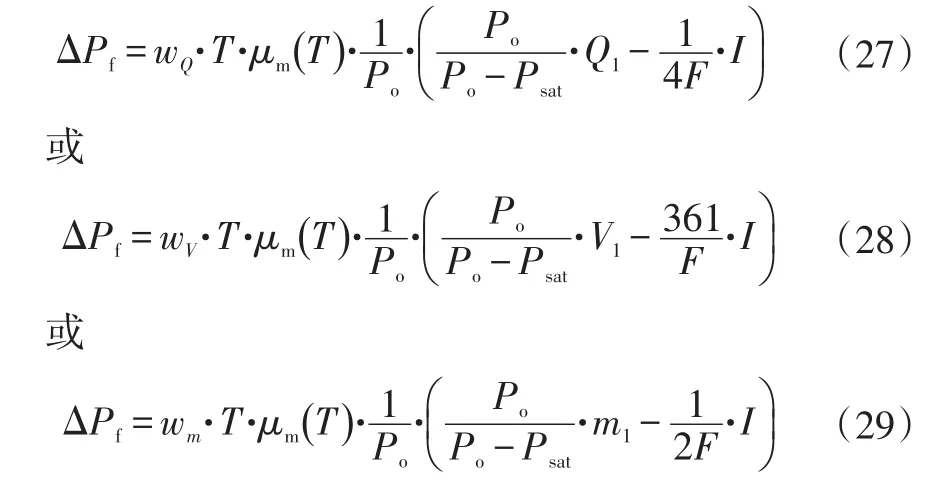
式中，V1为氢气的体积流量；m1为氢气的质量流量；wQ、wV、wm分别为待定系数。

待定系数与燃料电池流道特性有关，通过仅1个单相流工作点标定即可得出：

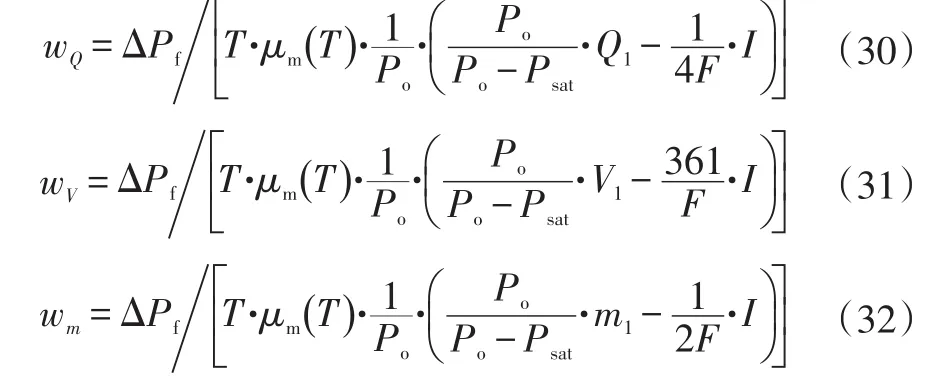
该模型实现了对氢气进气量与电流的解耦，且不需要燃料电池自身的精确参数。所述解耦的前提是燃料电池处于正常工作状态，解耦的结果是压降模型式（27）～式（29）中的第5项，即进气流量与一定倍率下输出电流的差。同时，该解耦模型可在计算燃料电池阳极压力降基准时输出电流与进气量作为独立输入变量，在燃料电池正常工作的前提下可分别研究进气流量或输出电流对压降基准的影响。

3 模型验证

3.1 试验设计

针对上述模型，本文设计了验证试验。试验电堆由1片燃料电池单体组成，流道类型为蛇形流道，MEA有效面积为260 cm2。根据模型推导过程，试验过程中将燃料电池电堆的流道参数设定为未知。试验平台由Green Light®公司提供，型号为G60。为精确监测燃料电池阳极侧进排气压降，压力降通过差压变送器获取，其量程为0～2 kPa。差压变送器信号通过外部数据采集卡获取，数据采集卡由National Instrument®提供，型号为NI USB-6009，采样频率为100 Hz，同时对采集到的压力降数据进行10周期的滑动滤波。试验过程中氢气路和空气路的流量、进口压力与相对湿度保持一致。为减小燃料电池对环境散热带来的试验误差，工作温度低于45℃时冷却水温度与进气温度相等，工作温度大于45℃后设定冷却水温度高于进气温度1.5℃，冷却水流量恒定为3 L/min。试验原理如图4所示。

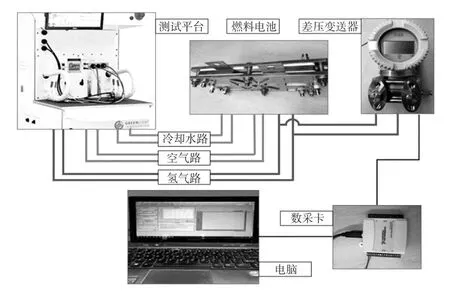
图4 试验原理

共进行3组试验：不同进气压力下的压降测试、不同工作电流下的压降测试和不同工作温度下的压降测试。各组试验的参数设置如表1所示。

表1 试验参数设置

对于第2组试验，由于燃料电池工作过程中会生成水，为维持单相流或近似单相流的工作状态，每个工作点的压力降数据为电堆输出电流从0切换到规定电流后的稳定压降值，每次输出电流的持续时间为10 s。两次试验之间，先通入干气体对燃料电池进行3 min吹扫，再通入相对湿度为98%的气体进行2 min吹扫，以保证下一次试验可以在单相流条件下进行。对于第3组试验，随着燃料电池温度的升高，电池对外散热逐渐增强，流道和配气管内容易冷凝形成液态水。因此，每次试验前先通入干气体对电池进行5 min吹扫，再通入相对湿度为98%的气体进行2 min吹扫，最后在20 min内连续记录数据并取平均值作为该次试验的测试结果。

3.2 试验结果分析

为减少凝露对试验的影响，试验过程中阴、阳极进气湿度设定为98%，整个试验过程中测试平台将进气相对湿度控制在0或90%～100%，偶尔有露点温度超过进气温度的情况，但是测试平台的管路设计保证了不会有过量的水分进入燃料电池。根据压力降模型，任一工作点可以求取模型待定系数。本文根据第1组试验的结果，通过算数平均获得模型待定系数为1.015 2×1010。由式（26）～（29）可得：

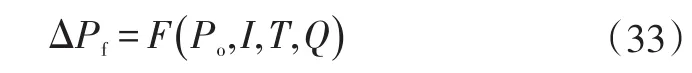
即压力降是进口压力、电流、工作温度和进气流量的函数。其中，对于函数第4项，前人已经进行了充分的证明[19-20]，本文不再验证。

第1组试验验证式（33）中进气压力对压力降的影响，从压力降模型可以得出，在其他条件不变的情况下，压力降与进气压力呈负相关关系，图5所示为试验结果与仿真结果的对比。从图5中可以看出，本模型很好地描述了进气压力对压力降的影响。

图5 不同进气压力下压降试验

第2组试验验证式（33）中输出电流对压力降的影响，经试验验证，本模型在满足较高精度的前提下实现了进气量与输出电流的解耦。解耦结果的验证需要在不同进气量与不同输出电流的组合条件下进行多次试验。本文的第1组、第3组试验测量了不同流量下的压降，压降与流量的关系得到了验证。为节省试验时间与成本，本文第2组试验在固定进气流量下进行了不同输出电流的试验。作为举例，图6所示为30℃、130 kPa条件下燃料电池输出电流由0变为40 A的仿真与试验结果。本组验证试验过程中，每次拉载瞬间的压力降测量结果相对仿真结果均有0.4～0.6 s的滞后，滞后可能是差压变送器的动态响应时间，或是负载变化引起的测试平台供气量的瞬时震荡产生的。如此迅速的瞬态特性对基于该模型的燃料电池含水量诊断不会产生明显影响。

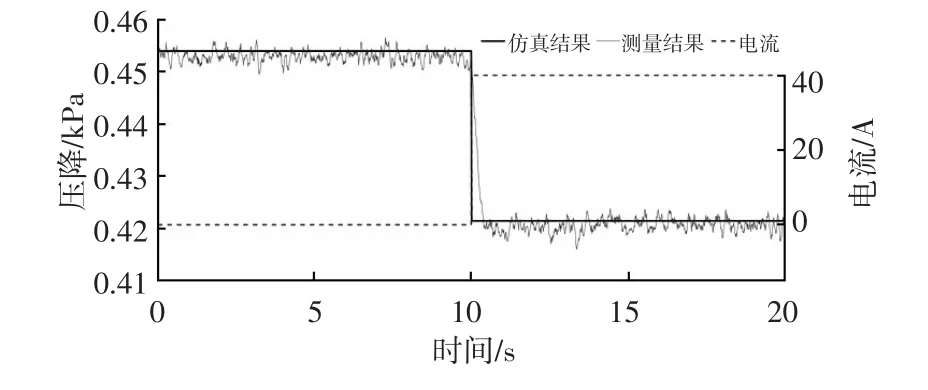
图6 拉载瞬间压力降变化

第3组试验验证式（33）中工作温度对压力降的影响：温度升高会造成压力降的线性增大；温度升高会造成混合气体粘度的非线性增大。因此，温度对于压力降的影响较为复杂。同时，燃料电池工作过程中的内部温度无法精确获取，通常以冷却水温度作为燃料电池的工作温度，进一步劣化了压力降模型对于物理现象的描述。图7所示为不同温度下燃料电池压力降与仿真结果的对比，在低温环境下（30～60℃）仿真结果与试验结果具有非常高的拟合度，最大偏差为6.96%。温度达到70℃后，仿真结果与试验结果相对误差有所增大，最大偏差为12.58%，这可能是燃料电池内部有少许冷凝水形成所致。但是采用童景山改进的混合气体粘度计算方法的压力降模型，仍然很好地描述了试验结果。

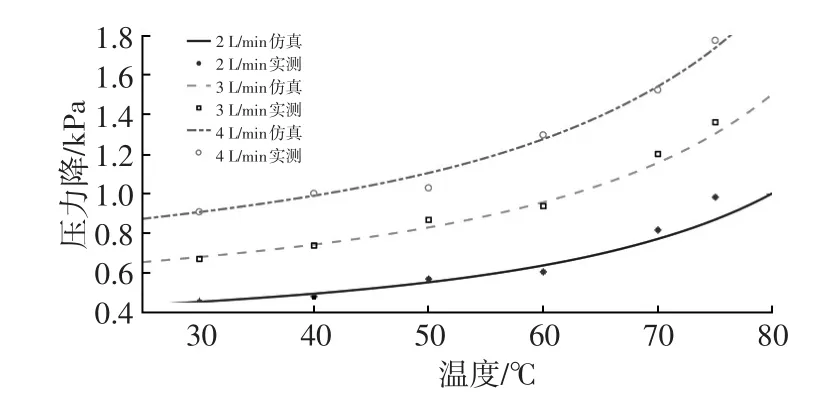
图7 不同温度下压力降试验

4 结束语

本文从含水量诊断的角度构建了一种单相流燃料电池阳极压力降模型。与前人的阳极侧压力降模型不同的是，本模型利用童景山的粘度结合因子计算公式，提高了模型的精度。同时，从控制的角度出发，模型实现了进气量与输出电流的解耦，而不必引入计量比作为模型的输入。主要结论为：

a.本文建立的用于阳极侧水淹诊断的单相流压力降模型与进气压力、工作温度、电流和进气流量有关；

b.本文从系统控制的角度实现了压力降模型的解耦，扩大了基于压力降的燃料电池含水量诊断方法的应用范围；

c.本文用童景山改进的混合气体粘度计算公式优化了以往文献中的饱和湿氢气的粘度计算方法，进一步提高了模型精度；

d.对于流道未知的燃料电池，本文给出了模型待定系数的标定方法。