基于三角模糊数-TOPSIS的既有高铁近接地基加固方案优选
邵国霞,曹政国
(1.西南交通大学土木工程学院,成都 610031; 2.中铁二院工程集团有限责任公司,成都 610031)
近年来,随着我国铁路建设事业的快速发展,新建铁路与既有高速铁路邻近或接轨(近接)的情况越来越多。由于相距较近,新建铁路在近接地段进行地基施工会对既有高速铁路产生不利的影响。为了保证既有高速铁路运营安全,在新建铁路设计时,需要选择安全适用、技术先进、经济合理的近接地基加固方案。但地基加固方案很多,各有优缺点和适用范围,如何在众多方案中选择最优的地基加固方案,是设计阶段急需解决的问题。
从目前的研究资料来看,专门研究近接高速铁路地基方案优选的文献很少,但应用于其他方面的方案优选方法却较多,对近接既有高速铁路地基方案优选具有一定的参考价值。已有的方案优选方法有:层次分析法[1,2]、三角模糊数-TOPSIS法[3-4]、模糊综合评判法[5,6]等。
既有高速铁路近接地基方案优选的影响指标众多,且多数的指标是不确定的、模糊的,其属性值与权重往往只能定性描述。层次分析法和模糊综合评判法在将定性描述向定量转化时,均可能由于表达信息的不完整而最终可能导致结果不符合实际情况[7];且这两种方法具有主观性较强,不能客观评判的缺点。三角模糊数对不确定事物采用可能发生的最大值、最小值以及最有可能值所组成的数序来进行精确描述,克服了用单个实数表达不完整的问题,适合于对定性描述的指标和权重的定量化,选用三角模糊数建立评价矩阵,更接近实际情况;TOPSIS法是一种适用于有限方案多属性决策的方法[3],而近接地基加固方案优选本身就是一个多属性决策问题,适合于用TOPSIS法进行决策。将三角模糊数与TOPSIS法相结合,对既有高铁近接地基加固方案中指标的属性值和权重定量化,并对近接工程地基加固方案作出合理的排序,为近接既有高铁地基加固方案优选提供一种科学的、可行的优选新方法,拓宽了三角模糊数-TOPSIS法的应用范围。
1 既有高铁近接地基加固方案优选指标
1.1 评价指标
既有高铁近接地基施工对既有高速铁路产生扰动,为了确保既有高速铁路运营安全,既有高速铁路的沉降要求为零[8],近接地基加固方案的选择至关重要。为了从初选的可行近接地基方案中选出最优方案,需要建立近接工程地基方案的优选评价指标,指标构建是否科学合理,对于地基加固方案优选结果有很大的影响。选取的既有高铁近接地基加固方案优选指标,不仅要满足工程造价、施工技术等基本要求,还要重点考虑既有高铁安全性的要求。鉴于此,参考国内外地基处理的评价指标[1,9-12],结合近接既有无砟高速铁路路基工程设计难点[13]及特点,建立近接既有高铁地基加固方案评价指标,见表1。

表1 近接既有高铁地基加固方案评价指标
以上6个指标中,工程造价为定量指标,其余为定性指标,它们对地基加固方案影响程度是不同的。
1.2 定性、定量指标的处理
定量指标可以精确计算,或用精确值表示。定性指标通常是用语言变量描述的。本文引入三角模糊数来解决定性指标量化问题。
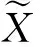
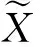
语言变量表示的定性指标用三角模糊数表示。
1.3 指标权重分析
专家不能准确给出指标权重的具体值的情况下,可以用语言变量给出。指标权重的语言变量通常是“非常不重要”、“不重要”、“不太重要”、“一般”、“比较重要”、“重要”、“非常重要”。将指标权重的语言变量转化为三角模糊数,见表2。

表2 指标权重与指标评价语言变量的三角模糊数对照
2 三角模糊数-TOPSIS优选模型[14-17]
2.1 建立三角模糊评价矩阵
设有A1、A2、…、Am共m个方案组成方案集,记为A={A1,A2,…,Am},每个方案有n个评价指标组成指标集,记为B={B1,B2,…,Bn};各个评价指标的权重为ω={ω1,ω2,…,ωn}。


(1)
2.2 规范化处理初始三角模糊评价矩阵

效益性指标规范化
(2)
其中
成本性指标规范化
(3)
其中

初始评价矩阵规范化处理后的结果为R′
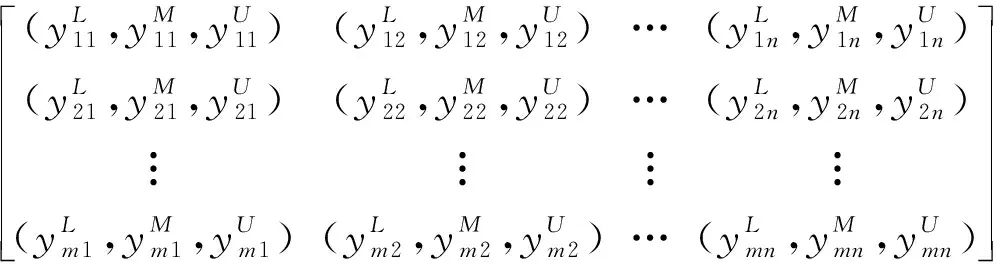
(4)
2.3 三角模糊数-TOPSIS优选模型的建立
(1)构造加权的规范评价矩阵
对已规范化的三角模糊评价矩阵R′进行加权,得加权之后的三角模糊矩阵Y
(5)

(2)确定模糊正理想方案Z+和模糊负理想方案Z-,即
Z+={Z1,Z2,…,Zn}
(6)

Z-={z1,z2,…,zn}
(7)


(8)
其中

(9)
其中
(4)计算方案Ai与模糊理想方案的相对贴近度Di
(5)排列方案的优先次序。按Di由大到小的顺序排列,排在前面的方案优先采用。
3 工程实例
新建曲阜至临沂城际线(简称曲临线)为有砟轨道,拟于上海端安全线股道10接轨,上联与京沪高铁股道Ⅱ线间距最近6.5 m,填高4.7 m,城际处帮宽6.25 m,下联临近京沪高铁股道Ⅰ。曲临线近接京沪高速铁路施工时,施工过程中相关作业如地基处理、路堤填筑、施工荷载等会不同程度导致高铁路基变形或受损。为了保证京沪高铁运行安全,需要对曲临线近接京沪高铁地基采取工程措施进行加固。根据曲临线与京沪高铁衔接处的地质情况、京沪高铁沉降控制要求等,初步选出技术上可行的4个地基加固方案:微型钢管桩、CFG桩、高压旋喷桩、挖除换填高强加筋复合轻质混凝土。评价指标为工程造价、处理效果、施工扰动、施工难易程度、安全性、施工经验,其中工程造价为定量指标,其余为定性指标。专家对初选出的4个方案各个指标给出评价,见表3。每个方案各个指标的属性值采用表2的三角模糊数形式给出,再采用三角模糊数-TOPSIS优选模型对各个备选方案进行评价。
3.1 建立三角模糊评价矩阵
通过表2语言变量及对应的三角模糊数,把表3各方案评价值进行整理得评价矩阵R。

3.2 规范化三角模糊评价矩阵
根据式(2)、式(3),对矩阵进行规范化,得矩阵R′

表3 各地基加固方案的指标评价值
3.3 建立加权的规范化评价矩阵
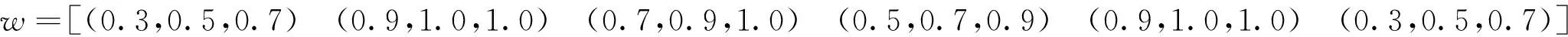
Y=wR′=

3.4 确定理想方案和负理想方案
Z+=[(0.3,0.5,0.7) (0.81,1.0,1.0)
(0.63,0.9,1.0) (0.35,0.7,0.9)
(0.504,1.0,1.0) (0.21,0.45,0.7)]
Z-=[(0.006,0.01,0.014) (0.45,0.7,1.0)
(0,0.09,0.33) (0.15,0.392,0.9)
(0,0.14,0.6) (0,0.055,0.301)]
3.5 计算方案Ai与模糊理想方案的距离与模糊负理想方案的距离
3.6 计算方案Ai与模糊理想方案的相对贴近度Di
D1=0.637 7D2=0.527 1
D3=0.551 4D4=0.356 8
根据以上所得各备选方案与理想方案的相对贴近度对方案进行排序,结果为:A1>A3>A2>A4,即在4个备选方案中,方案A1为最优。优选结果与既有文献[10]一致。
4 结论
通过对既有高铁近接地基方案优选研究,得出以下结论。
(1)结合近接工程特点,构建了由工程造价、处理效果、施工扰动、施工难易程度、安全性、施工经验6个既有高铁近接地基加固方案优选评价指标。
(2)基于三角模糊数并结合TOPSIS法构建了一种新的既有高铁近接地基加固方案优选模型。
(3)将三角模糊数-TOPSIS优选模型应用于曲临线近接京沪高铁地基加固方案优选实例中,各备选方案排序结果为:A1>A3>A2>A4,即方案A1为最优,优选结果与既有文献[10]一致。
(4)实践表明,该优选模型对既有高铁近接地基
加固方案进行优选是可行的,为设计方案优选提供一种新方法。

