从最小二乘法建模引出数学建模的“套路”

焦 华



从最小二乘法建模引出数学建模的“套路”

焦 华

（贵州商学院，贵州 贵阳 550014）

近十年来由于计算机与信息技术的迅猛发展,数学的应用领域已渗透到人类社会的每一个角落，其应用的深度和广度已超出了一般人的想象及认知。数学建模进入课堂已经成为世界教育的潮流。本文以最小二乘法作为案例诠释数学建模的“套路”，在勾画出数学建模框架基础上，对相关的数学思想、数学方法、数学历史、数学应用等浓墨重彩。目的是为数学建模教育研究“抛砖引玉”。

最小二乘法；数学建模；套路；Excel软件

0 引言

“套路”是2016年以来很流行的网络语言，也广泛应用到现实生活中，如“少一点套路，多一点真诚。”、“城市套路深，我要回农村。”、“自古深情留不住，总是套路得人心。”等等。百度搜索一下，“套路”一词是指精心策划的用于应对某种情况的方式方法，该词偏中性而在具体环境下略显贬义，网络上的“套路”趣味十足、娱乐性质较浓。在数学建模教学中使用这个流行词既能激发同学的学习兴趣，也使他们印象深刻。本文中的“套路”与上类同，但更强调客观事物的规律和特性；强调人类尊重客观规律采取的方法、制定的规则、执行的流程等。这里不讨论“武术套路”、“韩剧套路”、“传销套路”等，主要讨论与数学或计算机有关的“套路”：如初等行变换算法是线性代数贯穿始终的“套路”；构造辅助函数是微积分的特色“套路”；用循环结构实现“累加求和”是程序设计的“套路”（计算一项，累加一项。）。本文是将数学和计算机结合起来，探讨数学建模的“套路”。

数学建模论文包含有标题、摘要、关键词、正文、参考文献等，这与学术刊物公开发表的论文相似，也就是说两者“套路”相仿。但数学建模的正文部分是有特色的[1-2]，包含有：问题重述→合理假设→问题分析→模型建立及求解→结果分析→模型的检验→模型的评价与推广。 这是数学建模独有的“套路”。其中“模型建立及求解”是“套路”的核心，本文只讨论这个核心部分。

最小二乘法的出现是为了解决天体运动轨道的计算，历史上人们运用它重新找到了谷神星[3]，足以说明相关模型的建立及求解是正确的、合理的。本文以最小二乘法作为案例诠释数学建模的“套路”，是因为它是历史上数学建模应用成功的典型案例，同时也是通俗易懂的课堂教学内容。在数学建模的培训或课程教学中，如果一开始就选择难度较大的案例，学生听不懂将会失去兴趣、知难而退，因此选择合适的有应用背景的案例非常重要。（当前学生学习比较“急功近利”——想法是短时间内学有用的东西[4]。）通过此适中的案例可阐述清楚相关的数学思想、数学方法、数学历史、数学应用等，真正达到数学建模的根本目的。

1 最小二乘法的思想方法

最小二乘法是一种数学优化技术，是当前流行的机器学习最基础的算法，也称为最小平方（和）法。这种方法是用最小化误差的平方和来寻找已知数据的最佳函数匹配。使用最小二乘法能够方便地求得未知数据，并能使这些数据与实际数据之间误差的平方和达到最小。最小二乘法可从直线拟合推广到曲线拟合，即从线性回归推广到非线性回归。具体内容如下：

整理可得：

对上面方程用消元法求解得[5]：

提出问题和解决问题是数学的心脏，该问题的本质是寻找变量之间合理的函数关系，最后用微积分工具找到了答案。过程中包含了数学建模的核心“套路”——模型建立及求解。

2 最小二乘法的历史

19世纪的一个凌晨，意大利天文学家皮亚齐发现了一颗“没有尾巴的慧星”——谷神星。经过41天连续的跟踪观测后，终因疲劳过度累倒，醒来后找不到谷神星的位置。随后全球的天文学家及科学家们利用皮亚齐记载的观测数据寻找谷神星，但是依据大多数人的计算结果寻找谷神星都没有找到。24岁的“数学王子”高斯经过几个星期的刻苦研究，创立最小二乘法计算出谷神星的轨道。奥地利天文学家奥尔伯斯依据高斯的计算结果重新发现了谷神星[3]。这一事实充分展现了数学科学的威力。1809年高斯将创立的最小二乘法发表在他的著作《天体运动论》中。

数学精神是一种理性的、探索的、求真的精神，在数学建模或数学的教学中介绍相关的数学史，有利于培养学生的数学精神。数学知识的出现和发展起源于人类生产生活的需要，历史上数学知识的获得曲折动人，是一个不断修正错误、排除困难的过程。因此数学史的学习，有利于培养学生正确的数学思维方式，提高学生的创新能力。数学学科只能给我们知识，而数学历史却能给我们智慧。

3 最小二乘法的应用

在数学建模的“套路”（问题重述→合理假设→问题分析→模型建立及求解→结果分析→模型的检验→模型的评价与推广）中，这部分内容属于后期的“套路”，强调模型及求解方法的实际应用。

应用实例1：某成长型企业每年取得的净利润逐年上升，部分数据见下表。

试构建一个净利润作为时间函数的数学模型，并用这个模型对2021年的净利润进行预测。

解：先将此实际问题加以量化，确定自变量与因变量。为方便计算，设起始年1987年为0，并用表示，用（单位：百万）表示相应年份的企业净利润，于是可将上表转换得到下表[6]。

表1 年份与净利润对照表

Tab.1 Year vs. Net Profit

表2 年份间隔与净利润对照表

Tab.2 Annual Interval vs. Net Profit

这些数据点大致在一条直线上，根据最小二乘法待定系数的计算公式

因此该企业2021年的净利润预测为：38.5992（百万）元。

4 利用办公软件Excel做线性回归

数学建模过程中有很多复杂的运算和操作单纯靠纸和笔是难以完成的，需要利用计算机相关软件计算、验证、绘图等。常用数学建模软件有：Matlab[7-8]、Lingo、mathematica、Sas等，其实常被忽略的最基础的建模软件是Excel。在此仅用Excel实现数据的拟合。

步骤1：确定数据源，进入Excel窗口，在单元格A1、B1中分别输入,，在单元格A2—A12及B2—B12中分别输入,之值。注意这里数据源是纵向的，但也可以是横向的[6]。

步骤2：根据数据源绘制数据点的散点图，确定变量,之间的近似函数关系。具体操作是选中数据区域，选择“插入”→“图表”→“XY散点图”，根据操作提示得到散点图。这里要注意是由数据生成图表，两者是关联的。即数据源数据改变会引起散点图的改变。

选择“图表工具”→“布局”→“图表标题”→“坐标轴标题”，输入相关文字得下图。

单击散点图，选择“图表工具”→“布局”→“趋势线”→“线性趋势线”，可得下图。

图1 净利润与时间的函数散点图

图2 净利润与时间的函数线性趋势图

可以看出，直线与散点图拟合得很好。

步骤3：确定用线性回归方法后，接下来就是求待定系数a,b。

单元格A15中输入函数“=INTERCEPT(B2:B12, A2:A12)”，可得b=5.898；

单元格B16中输入函数“=SLOPE(B2:B12,A2: A12)”，可得a=0.9618。为了帮助对两个函数的记忆，如同单元格的表示要“先列后行”，函数括号中要“先后”。“INTERCEPT”与“SLOPE”按其英文单词的意思记忆，即“截距”与“斜率”。得到的结果图如下。

在上面的例子中，问题所给的净利润与时间的数据对之间大致呈现为线性关系，我们得到的回归曲线是一条直线，这类问题称为线性回归问题，它虽然简单但却具有广泛的应用价值，因为许多复杂的非线性回归问题，可以通过适当的变量替换将其化为线性回归问题来分析研究。以下就指数函数回归问题作为实例加以说明。

应用实例2：地高辛可用来治疗心脏病，医生对某个特定病人开出的初始剂量为0.5（毫克），此后时间（天）病人血液中地高辛的含量由下表给出。

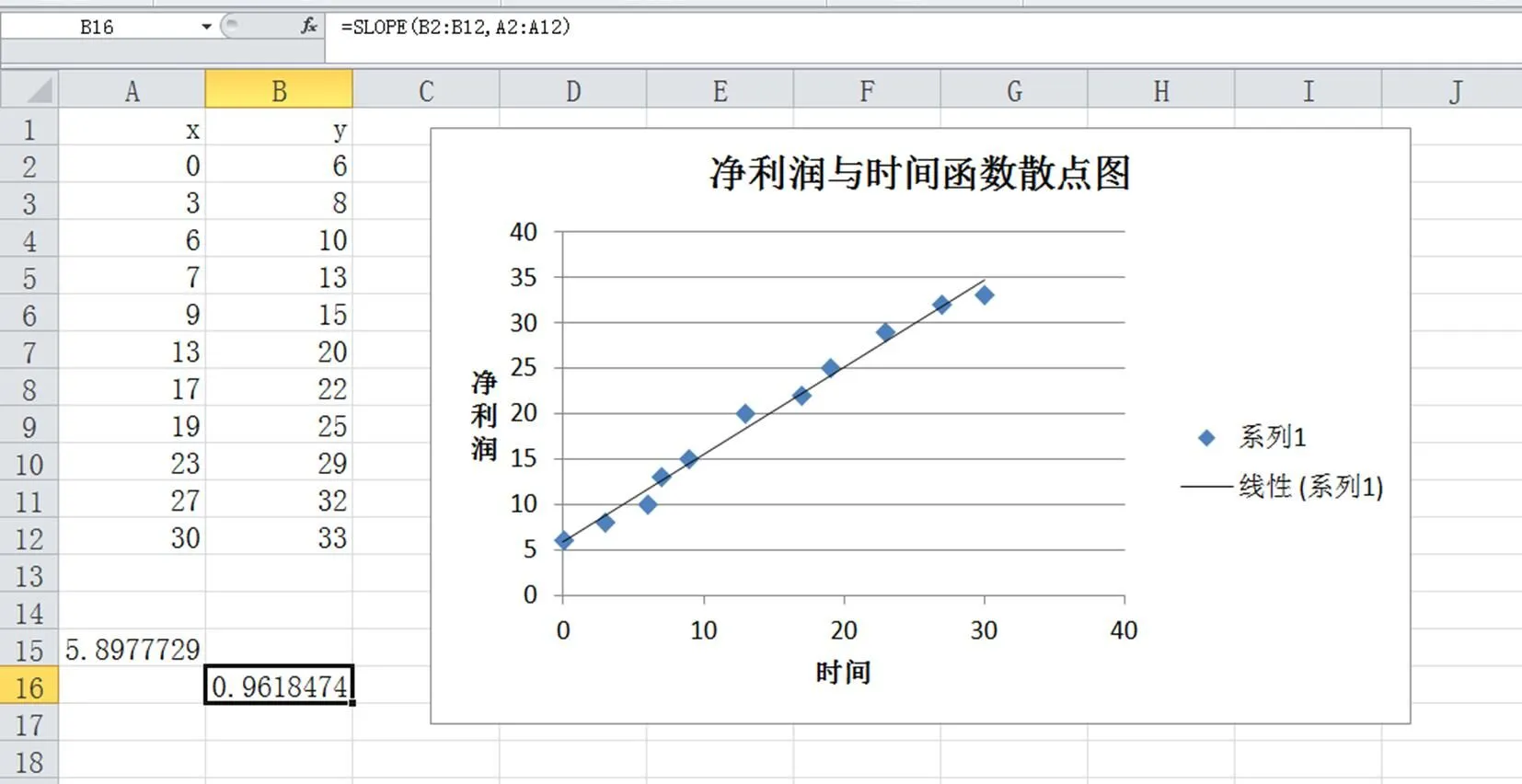
图3 线性函数斜率及截距计算图

表3 用药间隔天数与人体血液中地高辛含量对照表

Tab.3 Comparisons between days between medication and digoxin content in human blood

（1）试构建人体血液中地高辛含量与用药后天数之间近似函数关系。

（2）预测12天后人体血液中地高辛含量[6]。

解（1）将上表的数据填入EXCEL表格中，选中数据区域，选择“插入”→“图表”→“散点图”，这样得到用EXCEL作出的散点图如下。

从上图观察，y与x大致体现为指数函数关系，选择“图表工具”→“布局”→“趋势线”→“指数趋势线”，可得下图。

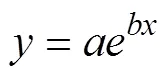
图4 用药天数与人体地高辛含量函数关系散点图

图5 用药天数与人体地高辛含量函数关系趋势线图

表4 取对数转换后的对照表

Tab.4 Comparisons after logarithmic conversion

图6 指数函数关系待定系数求解图

观察到图中回归曲线穿过所有的散点，由此可见该指数函数和散点拟合得相当好，进一步说明指数模型是非常合理的。

需要强调的是在选定散点图后[9-10]，使用“图表工具”→“布局”→“趋势线”→→“线性趋势线”或“指数趋势线”时，点击“线性趋势线”或“指数趋势线”按扭将触发EXCEL软件中的计算程序与绘图程序，而计算程序的算法就是最小二乘法！绘图程序描出的是回归函数的图像。

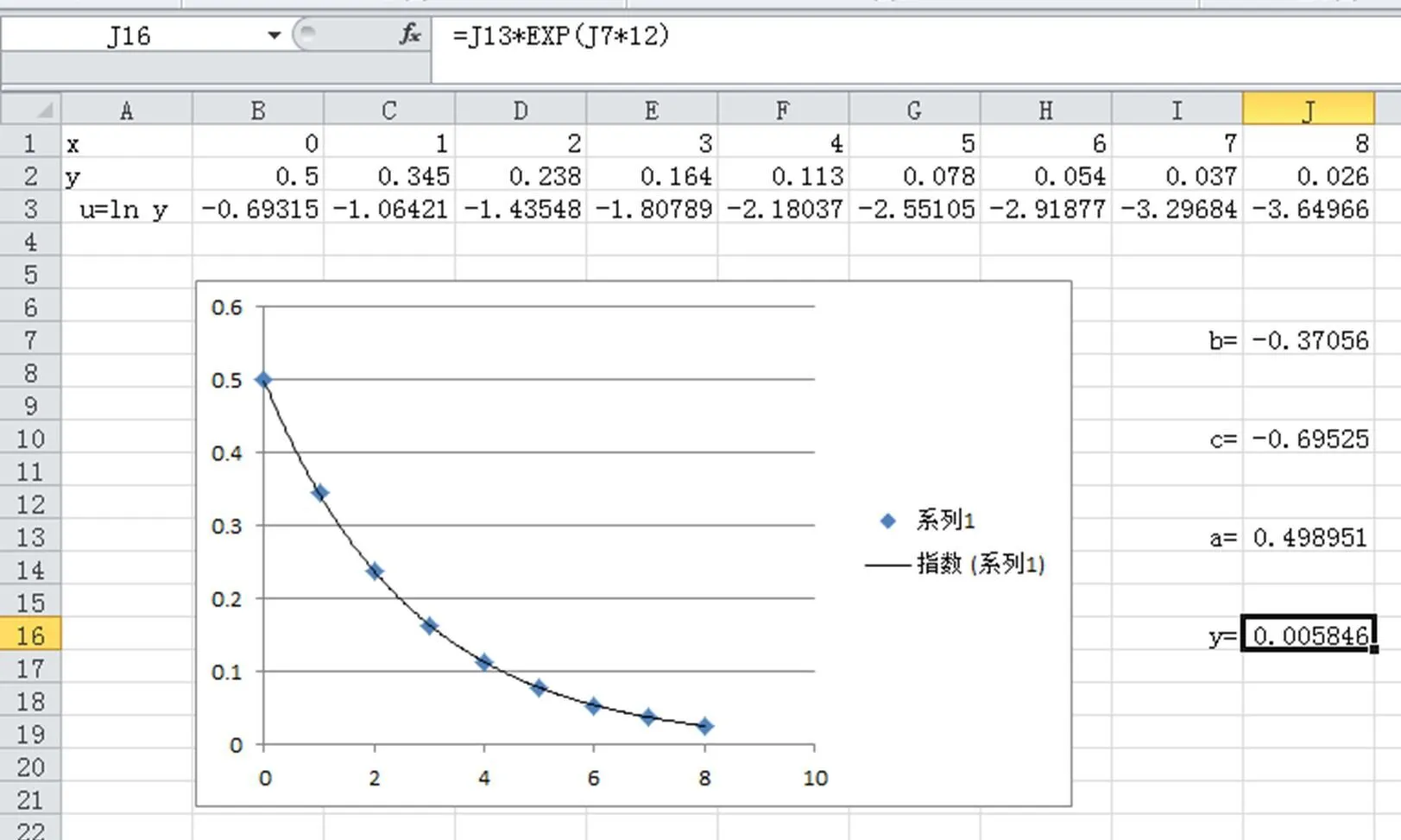
图7 指数函数关系预测值求解图

5 总结

数学是人类描述客观世界最基本的科学语言,是人类探索世界、改造世界重要的科学工具[11]。数学应用的广泛性推动着科技的进步，深刻影响着人类文明的进程。尤其是近70多年以来，计算机的出现和信息技术的迅猛发展,数学不仅广泛应用在工程技术、自然科学等领域，而且向经济管理、金融服务、环境能源等新的领域以空前的广度和深度渗透交叉。大数据、云计算、人工智能已经使数学成为当代高科技的基础和重要组成部分。

数学建模通俗地说就是依据实际问题建立数学模型，然后用数学方法和计算机工具对数学模型进行求解，最后根据结果去解决实际问题[12]。由于现今衡量一个国家的科技水平是根据这个国家消耗数学的程度，因此数学建模进入课堂已经成为世界教育的潮流。本文以最小二乘法建模案例引出数学建模的“套路”，目的是让学生能够“窥一斑而知全豹，见一叶而知深秋”。

[1] 姜启源. 数学模型(第五版)[M]. 高等教育出版社, 2017年.

[2] 张大坤, 史一苇, 任淑霞. 组合数学课程教学改革与实践[J]. 软件, 2018, 39(6): 205-208.

[3] 蔡天新. 数学简史 [M]. 中信出版集团, 2017年.

[4] 石黎, 孙志梅. 教学质量评价的BP 神经网络模型[J]. 软件, 2015, 36(3): 19-21.

[5] 吴赣昌. 微积分(经管类第五版)(下册)[M]. 中国人民大学出版社, 2017年.

[6] 吴赣昌. 微积分(经管类第五版)(上册)[M]. 中国人民大学出版社, 2017年.

[7] 徐治. Visual C++调用MATLAB 函数库的混合编程技术[J]. 软件, 2015, 36(2): 55-58.

[8] 雒明世, 张倩琳. 基于MATLAB 的OFDM 系统仿真与教学研究[J]. 软件, 2015, 36(6): 152-157.

[9] 王铁刚. 社交媒体数据的获取分析[J]. 软件, 2015, 36(2): 86-91.

[10] 卓广平. 数据挖掘开发及应用研究[J]. 软件, 2015, 36(5): 81-83.

[11] 张平文. 数学建模进入课堂已经成为世界教育的潮流 [J]. 数学教育学报, 2017年.

[12] 赖明治. 数学建模提供数学与现实生活的联结[J]. 数学教育学报, 2017年.

The “Method” of Mathematical Modeling is Derived From Least Squares Modeling

JIAO Hua

(Guizhou University of Commerce Guizhou, Guiyang 550014)

Because of the rapid development of computer and information technology in the past ten years, the application field of mathematics has penetrated into every corner of human society. The depth and breadth of its application have exceeded the imagination and cognition of the general people. Mathematical modeling has entered the trend of world education. In this paper, the least square method is used as a case to explain the "method" of mathematical modeling. On the basis of drawing out the framework of mathematical modeling, the relevant mathematical ideas, mathematical methods, mathematical history, and the application of mathematics are rich and heavy. The purpose is to contribute to the research of mathematical modeling education.

Least square method; Mathematical modeling; Method; Excel

O17; G642

A

10.3969/j.issn.1003-6970.2018.12.011

贵州省教育厅2016年本科教学工程项目(项目编号：SJ-JXGC-KC-003、SJ-JXGC-KC-002)

焦华，男，硕士研究生，贵州商学院计算机与信息工程学院副教授，研究方向：算法与程序。

焦华. 从最小二乘法建模引出数学建模的“套路”[J]. 软件，2018，39（12）：44-50