江户时代日本学者对《授时历》五星推步的历理分析
徐泽林
(东华大学人文学院,上海 201620)
中国传统科学因注重实用而带有技术化特征,忽视对原理的清晰阐述,加之天文历法又是古代社会中的帝王之学,具有绝对的权威性和神秘性,所以正史“历志”通常只载推步之法,不叙其原理,这给后世解读增添困难。行星运动理论是西方传统天文学的核心内容,影响着西方天文学的发展。对五大行星视运动的推算也是中国传统历法的重要内容,但其精度不及日月运动的推算,数理科学水平较高的《授时历》(1280)也没有对五星运动推算的原理给出清晰的阐述。学术界对中国古代天文历学中五星运动推算的精度与理论问题展开了一系列研究,薮内清(1906~2000)、刘金沂(1942~1987)、宫岛一彦、陈美东(1942~2008)分别对隋唐历法中五星推步算法进行了疏解和数理研究[1-4],张健、李勇分析了《授时历》和《大统历》中五星推步算法的精度问题[5-6],陈美东讨论了中国古代对五星近日点黄经及其进动值的测算问题[7],钮卫星与武田时昌通过文献考证和数理分析探讨了早期历法和一些天文材料中有关内行星运动数值的来源问题[8-9]。曲安京、中山茂(1928~2014)以《授时历》为中心,探讨了五星推步算法的构建原理以及古代行星运动理论问题[10-11]。最近几年,唐泉在研究古代历法中五星运动方面用力最多,他在总结回顾学术界关于五星运动研究成果的基础上[12],对古代历法中五星推步算法的历史沿革做了梳理[13-14],并且还分析了唐、宋、元时代一些重要历法中五星盈缩差算法的构造与数值精度问题[15-20]。以上这些丰富而深刻的研究成果有助于我们认识中国古代行星运动计算方法的历史发展及其科学意义。但是仍然存在一些问题值得进一步探讨,如五星推步算法的构建原理问题,特别是如何解释《授时历》中的“限度”概念,以及内行星盈缩差公式中系数来源及其天文意义等问题。
考察日本江户时代关于《授时历》的注解书可以发现,日本学者对这些问题早有讨论。中西敬房在其《历学法数原》(1787)中,引用清初黄鼎《天文大成管窥辑要》的说法,解释了五星运动的成因,质疑五星推步算法引入“限度”概念不合行星视运动的实际状态,并怀疑行星推算精度不高可能与引入“限度”这个参数有关。在其前,著名和算家建部贤弘(1664~1739)在其《授时历术解》中对“限度”意义已给出了解释,同时解释了五星盈缩差算法公式的数学意义,特别是内行星公式中系数的数学意义。约19世纪初,大野正辰在《授时历秘诀》(19世纪初)对内行星公式中系数的意义也给出数学解释。江户时代的这些注解有助于我们对中国古代行星运动理论以及数理科学的认识。本文首先论述分析这些注解内容,并在这些注解以及前人相关研究工作的基础上,再次分析《授时历》五星推步算法的构造原理,旨在复原中国天文历学家构造五星运动算法的思路,由此揭示中国传统数理科学的特点。
1 《授时历》中的五星推步算法及其问题点
《授时历》的五星推步内容基本沿袭《重修大明历》(1127),只是一些天文常数做了改进,其算法上的进步主要反映在引进了平立定三差法以计算五星运动盈缩差,但算法整体结构没有发生变化。围绕推求行星视运动过程中合、伏、见的时刻与真黄经,《授时历经》给出五星动态表以及18个推步之术。为便于说明其算法构建原理,这里再次以符号代数语言概述其算法。
如图1,规定公元1280年冬至时刻(历元O0)为历法推算起点,记回归年长度(岁实)为T=365.2425日,周天度数(历度)为C=365.2575度,行星与太阳的会合周期(周率)为H,行星公转周期(历率)为S,行星运行1度所需要的日数(度率)为ϑ=H/(H-T),历元(O0)前最近距的平合点(H1)到历元的时间间隔(合应)为Δh,历元(O0)前最近距的入历点T0(称作盈初)到历元的时间间隔(历应)为Δp,行星盈缩差公式的三项系数分别为a、b、c,即行星盈缩差y=f(λ)=[a±(b±cλ)λ]λ(λ为入历限数),太阳盈缩差公式的三项系数分别为e、f、g,即太阳盈缩差cs=p(z)=[e±(f±gz)z]z(z为入历限数)。

图1 五星推步算法背景示意图
在一个会合周期内,行星经历合伏、顺行、留、逆行、留、顺行、合伏的运动状态,为此将五星运动状态构建成五星动态表(各星运动状态划分不等的若干个阶段,木星分14段,火星分18段、土星分12段,金星分20段、木星分10段)。例如木星动态表(表1):

表1 《授时历》外行星运动动态表(木星)
表1中,段目(i)指该段的名称;段日(di)为行星处于该段的平均时长;平度(αi)指在该段日数内之行星平行的积度,也就是行星处在该段的平均角度;限度(μi)是用于计算行星处于该段的入历度与盈缩差的参数;初行率(vi)是行星处于该段的初始速度。动态表描述了五星处于各段的初始时间与位置状态,相当于给出其对应的平时间与平位置,其精确的实际值则根据推步之术计算获得。
《授时历》中由18个术构成的五星推步算法可以归纳为四个计算过程:首先推求所求年的冬至时刻以及冬至后平合的平时刻与平黄经;其次借助五星动态表,推求诸段的平时与平黄经;再次进行行星运动改正(五星盈缩差);最后进行太阳运动改正(距合差度与太阳盈缩差)而获得确定的位置。将其进一步概括为三个核心步骤:
(1)首先推求所求年冬至后平合及诸段的中积与中星,也就是推求从所求年冬至(O)后的平合(A0)及诸动态阶段(Am)分别到所求年冬至(O)的平时γm(称作中积)与平黄经ωm(称作中星)。假设所求年冬至(O)至历元(O0)共积Nn年,那么由Nn×T+Δh≡hk(modH)与hk+1=H-hk,求出前合分hk与后合分hk+1,后合分hk+1除以日周(10000分/日或10000分/度),得到后平合的中积γ0(以日为单位)与后平合的中星ω0(以度为单位)。于是,在此数值上分别累加段日di与平度αi,就分别得到诸段的中积为γm=γ0+x和诸段的中星为ωm=ω0+β(x=Σdi,β=Σαi)。
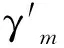
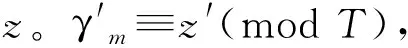
第二步,推求平合及诸段第一日的行差的σ,也就是求行星与太阳的初始速度差。一般情况下,该段第一日行差σ为该段初日行星行分va与太阳行分vs之差,即σ=|va-vs|。但是,对于金、水二星退行在退合场合,σ=va+vs,对于水星夕伏晨见场合,σ=vs。
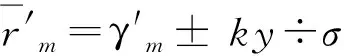
以上概括了五星推算的最主要算法步骤。针对这些算法,学术界展开了系列研究和讨论,问题聚焦于以下几个问题:
(1)五星推步算法的精度如何?
(2)在五星推步中“限度”概念如何理解?它具有怎样的物理意义和数学意义?
(3)在推算五星盈缩差时,内行星的公式中乘率k是如何获得的(同样,求内行星运动中定诸段泛积的公式中,系数k的来源也不清楚)?
(4)五星盈缩差是否就是行星中心差?五星盈缩差的天文学意义是什么?
(5)行星真黄经计算公式的构造乃至五星推步算法的构建原理是什么?
对于问题(1),前述文献都有论述。后面几个问题,学术界常采用近代西方天文学方式给出解释。本文根据江户时代日本学者的注解,在前人相关研究的基础上,对后面几个问题再作一些探讨,试图以东方数值分析方式给出一种解释。
2 江户时代日本学者对《授时历》五星推步算法的注解
与清代以西方古典数理天文学理论和方法编制历法的环境不同,日本江户时代最初以《授时历》为范本编制历法。因此,《授时历》在日本江户时代的影响远超在本土清代的影响。石云里曾经调查了日本江户时代的《授时历》注解书,列了20余种[21]。近年来笔者进一步调查,发现江户时代关于《授时历》的注解书达60余种之多。这些注解书对五星推步问题也有所注解,主要有中西敬房的《历学法数原》、建部贤弘的《授时历术解》和大野正辰的《授时历秘诀》。
2.1 对《授时历》中“限度”概念的解释
2.1.1 中西敬房对“限度”概念的疑惑
中西敬房(?~1781),字如环,通称宇兵卫,号华文轩,是活跃于江户时代中期的历算家与气象学家,在京都经营书店同时兼修关流算学与天文历学。明和四年(1767)刊行《浑天民用晴雨便览》,为日本历史上最早的气象方面的著述。此外,还著有《风雨赋国字弁》(1776)与《历学法数原》(1787)等。
中西有感于《授时历》记载的推步法过于简略,更不论法原,故“据《明史》及诸书[注]指黄鼎的《天文大成管窥辑要》及梅文鼎的《梅氏历算全书》等中国天文历学书籍。而详其法数,且补阙略,以为造历者之鉴本,号曰:《历学法数原》”[22]。该书分“法原门”与“数原门”两部分。前者据《明史·历志》论历算的数学原理,包括勾股测望、弧矢割圆、黄赤道差、黄赤道内外度、白道交周、日月五星平立定三差、里差刻漏等内容。后者据《授时历》术文论推步之术,包括步气朔、步发敛、步日躔、步月离、步中星、步交会、步五星等内容。该书基本是对《明史·历志》《天文大成管窥辑要》《历算全书》等书讨论《授时历》的有关内容的转述,其间也夹杂一些作者的议论。值得注意的是,该书卷5的最末有一段“论五星各段限度”的文字:
按如本经所载五星限度者,明大统历直采用之,而本邦古历亦从焉。其于法原,《元史》原阙略矣,《大统通轨》亦只用其度而无敢议论其原者《管窥辑要》及《历算全书》亦然,此无他,所以其理之所由未审也。愚亦考之尚矣,虽然不敏之性未能知觉其法原也。
按如五星平度,各星平合距次平合迟疾退一周之度,故实测各段平度以累加诸段中星而求次段中星者,宜也,其于限度累加五星平合入历度,以求诸段入历度者,恐不是乎?按:《管窥辑要》所谓“五星之行,其迟疾也,有本于星者、有系于日者、有由乎气者。三法具而步星之法益密”云云。顾夫五星各合伏距合伏之间,近于太阳则其行疾,远于太阳则其行迟。是以五星平度既有疾迟之多寡,此所谓系于日者也。且从其性情,五星各有自行之不同,木星日行九十一分奇,火星日行四十六分奇,土星日行九十六分奇,金星六十二分奇,水星三度一十五分奇,故五星周率各不同,此所谓本于星者也。尚有入气之差,故五星各立三差之法而推求入气盈缩之差,以加减常积,则可得其逐段之定度,此所谓由乎气者也。方今三法已备焉,何再用限度哉?且夫本经所载五星退段各用顺度。按:退行之时,岂得有顺度耶?是可疑。盖依经术而求五星躔度间有差一二度者,限度之误乎?或曰:然则求入历诸段何以累加之耶?日俱以平度可累加,此与累加中星为诸段中星同理也。如本经用限度,疑王恂未定之初稿而非郭太史续定之法欤?此予一遍[注]当为“偏”,原文误作“遍”。之臆见也。若有乖戾,则君子订正之,虽我没后,亦泉下之幸也矣。[22]
中西敬房的这段注文至少包含以下几层意思:
(1)他首次指出,在《授时历》《大统历》乃至明清历学家的著述中,均没有论及《授时历》中“限度”概念的意义。他自己注意到了这一问题,但也一直没有搞清楚。
(2)他引用清初学者黄鼎的《天文大成管窥辑要》中关于五星运动成因的说法,认为五星运动迟疾的成因有三:“有本于星者、有系于日者、有由乎气者”。所谓“本于星者”,即各星周率不同,有各自的运行速度,其本质是指各行星在其恒星周期内由于轨道半径不同,有其各自不同的绕太阳公转速度。所谓“系于日”者,指五星从合伏到下次合伏期间,接近太阳则疾行,远离太阳则迟行。这是由于五星平度既有疾迟多寡,则与太阳的角距为0时速度最大,以后与太阳距角越大则速度越小。所谓“由乎气”者,指五星运动有“入气之差”,用招差法推求入气盈缩差,以加减于常积,则可得到各运动状态的定度。这是由于地球绕太阳公转相对于行星位置变化而造成的,以地球上的观测者来看,行星伴日沿黄道做非匀速运行,在不同节气运动速度不一样。
(3)中西根据黄鼎的五星运动迟疾成因说,对《授时历》中使用“限度”这一参数进行计算的方法提出了质疑,怀疑以此计算是多余的。他怀疑的理由可以归纳为以下两点:第一,在五星推步中,黄鼎所论五星迟疾成因之三因素都已具备了,而且有三差法计算入气盈缩差,因此就没有必要使用“限度”了;第二,在利用“限度”计算时,在行星退行场合会出现计算出“顺度”的情况。进而他猜测,按照“历经”的术文计算五星躔度时存在一二度的误差,可能是因为使用了“限度”而产生的。
(4)怀疑现存使用“限度”计算的《授时历经》是王恂的草稿,而非郭守敬续定的算法。
中西的以上困惑,引发了日本科学史家薮内清和中山茂的疑问[23-24]。其实,在中西之前,建部贤弘在《授时历术解》中已经给出了解释,因建部贤弘的注解书是未刊刻的抄本,所以中西没有看到。
2.1.2 建部贤弘对“限度”的解释
被认为是建部贤弘著述的抄本“六卷抄”(包括《授时历议解》3 卷、《授时历术解》2卷及《授时历数解》1 卷)是江户时代关于《授时历》的众多注解书中内容最为丰富、解释最为清晰深刻的著作。其中《授时历术解》对五星推步也作了详细注解,在五星运行动态表后对“限度”给出了解释,在五星推步的“求五星定合之定积与定星”的术文之后,对内行星计算公式中的乘率也给出了解释,并且给出自己的计算公式。我们首先以木星为例,来检讨建部对五星运行动态表中相关概念的注解。其注文如下:
平度,随各段之日数,星之平行积度也。自合到见,十六日八十六分,星行三度八十六分;疾初二十八日,星行六度一十一分;疾末二十八日,星行五度五十一分;迟初二十八日,星行四度三十一分;迟末二十八日,星行一度九十一分也。留无行分,退四十六日五十八分,星行四度八十八分也,分下秒数带于退段。是测考算定而所得也。
限度,各段入历行度也。非星之所当,作为平日之所当而算定之入历度数也。例如,星行盈历时,顺行分比常行多,故积顺行之日过星平度,故有盈差;逆行分比常行少,故虽言星退,然犹增盈差。星行缩历时,顺行分比常行少,故积顺行之日后星平度,故有缩差;逆行分比常行多,故虽言星退,然犹增缩差。故于退段,平度减度数而得中星,限度加度数而求盈缩之增差,是所立平度数与限度数所以异也。然从合到合,积度之数不当,令其适合。先倍所定退段之限度三十二分,以减一周积度,余三十三度为顺段之历积度。又累计顺段前后之平度,得四十三度四十分,为星积度;置各顺段平度,乘历积度,以星积度除之,得各段限度。其周天秒数带退段。
初行率,各段初日之常行度分也。依本经之术以各段日除各段平度,为各段平行分,得合伏二十二分八九,疾初二十一分八二,疾末一十九分六八,迟初一十五分三九,迟末六分八二,退十分四八。末段前后平行分相减,倍而退一位,为增减差,得疾初六十四秒,疾末一分二十九,迟初二分五十七,各加于其段平行分,得疾初、疾末、迟初三段之初行率。求合伏,倍疾初段增减差,疾初日数内减一,余二十七除,得日差五秒,半之,加疾初初行率,得二十二分四九,为合伏段之末日行分。以是减合伏段平行度,余四十秒,为增减差,加于平行分,得合伏段初行率。求迟末,倍迟初段增减差,迟初日数内减一,以余除,得日差十九秒,倍之,得三十八,又以迟初段增减差,减其平行分,余一十二分八二为迟初段之末日行分,倍日差,减而余为迟末段初行率。求退段,不用本术六因,依旧法,本行分十四乘十五除,为总差,半而为增减差,加于退段平行分而为后退段初行率。皆分下秒数五以上收为一,五已下弃之。又术,于疾与迟之限,各立三差之法,得平度。求初行亦同。[注]《授时历术解》的注释原文为日文,现以文言汉译。下同。[25]

顺行的平度αi之和:β=Σαi=43度40分(星积度);
逆行的平度āi之和:βr=Σāi=4.88125×2=9度76分25秒;
木星东行:β-βr=Σαi-Σāi=33度63分75秒(一周积度);
逆行时段的限度和:τr=Σūi=0.32875×2=0.6575度;
顺行时段的限度和:τ=β-βr-τr=32度98分(历积度);
各顺行时段的限度:μi=αi×[(Σαi-βr-τr)÷(Σαi)]=αi×(32.98÷43.4)。
至于如何确定退行时段的限度(0.32875×2),建部没有说明,曲安京对这个问题有过解释[26]。
对于为什么要引入“限度”,建部也做出了说明,他说:
例如,星行盈历时,顺行分比常行多,故积顺行之日过星平度,故有盈差;逆行分比常行少,故虽言星退,然犹增盈差。星行缩历时,顺行分比常行少,故积顺行之日后星平度,故有缩差;逆行分比常行多,故虽言星退,然犹增缩差。故于退段,平度减度数而得中星,限度加度数而求盈缩之增差,是所立平度数与限度数所以异也。[25]
也就是说,因为行星在退行时,虽说是退行,但仍然存在增加的盈差,为了求其盈缩的增差,所以建立不同于平度的“限度”概念。建部这样的认识十分精辟,关于这一点,笔者在后面将作进一步的分析。
2.2 对《授时历》中求内行星定度定星算法的解释
2.2.1 建部贤弘的解释
其段中星,第一条所求,即自天正冬至到其段平日加时之积度也。○盈缩差,第三条所求,即自其段平日所当,距盈后、缩前常日所当之度分也。○金星倍之,水星三之,盈缩差金倍之、水三之而加减也。○黄道日度,日躔第七条所求也。○术意:置其段中星之度分,盈差加、缩差减,而得自冬至加时到其段常日加时星所在之度分,为诸段定星。加天正冬至加时黄道日度,累去黄道宿次之度分,而得星所在之宿度也。用其盈缩差,金星最疾行一度余也,故随自其平日到常日之日分,定积日之所当也。又星行盈在后、缩在前,如始之盈缩差,故定积之日定星所在,比中星之度,盈缩差之一倍也。依之,盈缩差加减于中积而为常日定积,倍差,加减于中星而为定星。水星最疾行一度余也,故随自其平日到常日之日分,定积日之当所也。又星行盈在后、缩在前,如始之盈缩差之一倍也,故定积之日定星所在,比中星之度,盈缩差之三倍也,依之,盈缩差加减于中积而为常日定积,三之差,加减于中星而为定星也。
今按:金水二星如此求者,于顺之合、见、伏段宜粗,然于退合,非倍、三之限,各段又随星行分倍数甚有增减,求之者,以其段初行率乘盈缩差,百约,所得为定积加时盈缩差,又并盈缩差,以加减中星,可得定星积度。木、火、土三星亦可如此求,如何?于三星有无星行分乎?[25]

2.2.2 大野正辰的解释
在建部贤弘之后,大野正辰在其抄本著作《授时历秘诀》中对“金星倍之,水星三之”也给出一种解释,并附示意图(图2)。其注解文字如下:
“金星倍之,水星三之”者,皆指盈缩差而言之。假令日行其盈缩差度,金星亦行之,然则其度倍也。水星行常,大凡倍日行,故日行其盈缩差度,水星行其度倍之,然则其度三倍也。
水星之行分常多于日,故日辰进退一日则星进退二度而有差,故为三倍;金星日辰有进退,则金星亦进退其度而又有差,故倍之。[27]
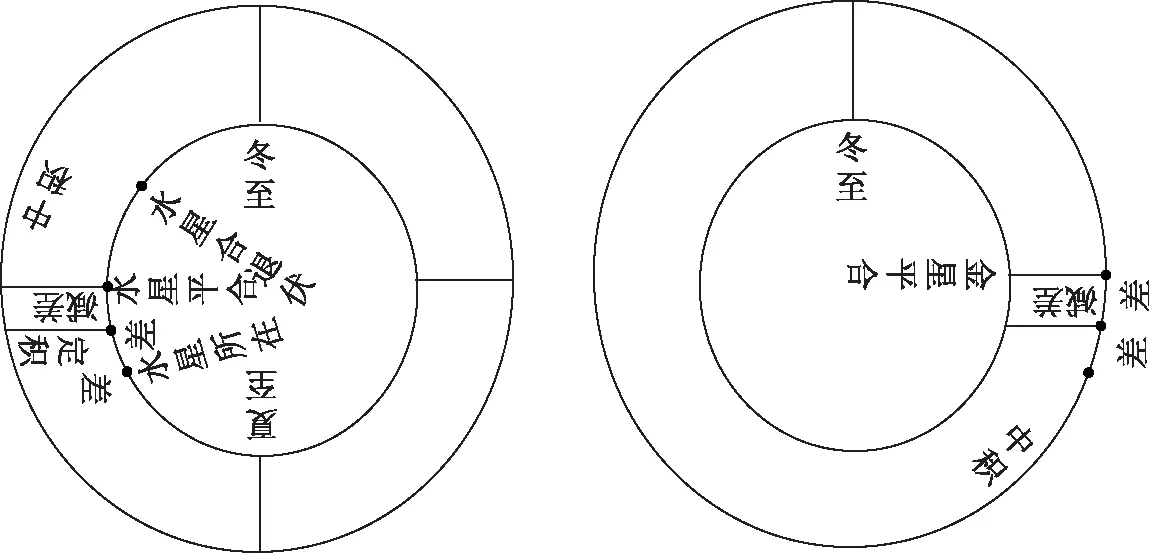
图2 大野正辰解释求金水二星平合定星的示意图
这段注解文字意思是说,太阳一天行一度,金星也一天行一度,当太阳运行其盈缩差的度数时,金星也运行了这么多度数,所以一共运行了两倍的盈缩差。水星平行速度是太阳的两倍,所以太阳运行其盈缩差的度数时,水星运行其盈缩差度数的两倍,一共运行其盈缩差度数的三倍。大野正辰的解释及其示意图也同样只是数量关系上的说明,没有反映这一算法的天文意义。
3 基于建部解释的五星推步原理分析
曲安京曾经用几何模型和微积分语言构造了外行星盈缩差算法的理论模型,以阐释中国古代历法中行星运动理论,但对内行星算法的分析付之阙如[10]。唐泉在此基础上,以同样的方式进一步构造了内行星盈缩差算法的理论模型[15]。他们的工作基本揭示了古代五星推步算法的科学原理,这是研究中国科学史必要的工作。当然,中国古代天文家不会利用西方式的几何模型来构建算法,并且五星推步中的五星盈缩差与太阳盈缩差并不等同于西方天文学中的中心差概念,在此情况下用西方几何模型的解释难以复原古代建构五星推步算法思路。中山茂根据建部对“限度”的注解,以东方固有的纯代数方式来构建五星推步的算法模型[11],尽管他也不主张使用西方天文学的理论与概念来解释中国天文学中的行星运动,但他还是使用了“中心差”概念。中山茂认为,从建部的注解来看,五星推步中考虑了两种中心差,一个是行星的中心差,再一个是太阳的中心差。入历,相当于“行星近日点”概念;冬至点,相当于“太阳近地点”,盈缩,相当于“中心差”。五星推步算法只是在直线上让太阳中心差与行星中心差叠加而已(如图3)。

图3 中山茂描绘的五星推步算法原理示意图
在中山的图示(图3)中,计算行星中心差的自变量,是从平合起度量的平度之和Σαi,加上平合到入历点的距离λ0;计算太阳中心差的自变量,是从平合起度量的限度之和Σui,加上平合到冬至点的距离γ0。即
行星中心差=Fp(λ0+Σ平度),应用行星中心差公式(平立定三差公式)或查表求出Fp;
太阳中心差=Fs(γ0+Σ限度),应用太阳中心差公式(平立定三差公式)或查表求出Fs。
行星的平均运动是会合周期内行星位置上的平度和,常度是平度加行星中心差所得,定度是加行星与太阳的两个中心差所得,由此得到行星的真位置。即
常度=Σ常平度+行星中心差
定度=Σ定平度+行星中心差+太阳中心差
但是,仔细考察《授时历》中五星推步的算法,不难发现,中山茂的解释存在一些错误和不足。首先,中山将计算行星“中心差”与太阳“中心差”的公式搞错了,计算行星“中心差”的自变量,不是其平度之和,而是“限度”之和,应该为“行星中心差=Fp(λ0+Σ限度)”;计算太阳“中心差”的自变量,不是“限度”之和,而是平合及诸段的定积(即行星运动第一次改正后的黄经度)的函数,应该是“太阳中心差=Fs(γ0+诸段定积的函数)”。其次,中山将《授时历》计算行星确定位置的算法简单化了。
下面我们根据《授时历》五星推步的算法步骤与建部贤弘的注解,采用中国古代数学与天文学中常用的数值方法,尽可能不使用西方天文学的理论,分析复原五星推步算法的构建思路。
太阳与行星会合运动的物理背景是在黄道附近两个运动体的追及运动,根据中西敬房所引黄鼎之论,“五星之行,其迟疾也,有本于星者、有系于日者、有由乎气者。三法具而步星之法益密”,表明古人对五星不均匀运动的成因归之于“本于星”“系于日”“由乎气”三者,其推步法的立术也当基于此。建部贤弘对此有更进一步的论述:“凡五星各有自行而运旋于天,星之本质也。有迟速之行分者,据太阳也;有盈缩进退者,据天度也;有见匿早晚者,据岁日也。是测验推算而立法术之所以也。”[25]据此我们假想有四条运动直线,即将太阳与行星的运动放在四条数轴上考虑逐步进行误差改正[注]当然,古人不会有数轴概念,也未必分解为四种直线运动。这样的分解只是为了解析算法结构。(如图4):在数轴(1)上刻画太阳的平行与行星的平行;在数轴(2)上刻画根据行星平行计算出来的“限度”变化;在数轴(3)上刻画行星运动改正后的行星实行变化;在数轴(4)上刻画太阳运动改正后的太阳与行星的实行变化。

图4 五星推步算法原理示意图
首先,在数轴(1)上计算平合A0及诸段Am位置的中积(γ0及γm)与中星(ω0及ωm),相当于确定平合A0及诸段Am位置的平时γm=γ0+Σdi与平黄经ωm=ω0+Σαi。
其次,在数轴(2)上计算限度um,用于计算行星自身运动的改正量y(行星盈缩差)。一般情况下,天文学上总是由天体的平黄经计算出其真黄经。由于日月在黄道上没有退行现象,所以对于日月非均匀运动的计算,都是应用招差法直接由其平黄经计算运动改正量,通过对平黄经的修正确定其真黄经。但是,行星在黄道上有退行,所以不能直接以其平黄经来计算其运动改正量。在一个会合周期内,行星一共顺行β=Σαi平度(星积度),退行βr=Σāi平度,所以视运动上向东平行了β-βr=Σαi-Σāi度(一周积度),但其实行之中还有黄经的减少,减少量就是对应于退行平度βr度对应的退行限度τr=Σūi,因此,把Σαi-βr-τr度数看成是一个会合周期内行星在黄道上非均匀运动向东位移的黄经总量,其运动自变量被称作“限度”(历法中常把函数自变量称作限数,限度名称当由此而来),并把各顺段限度ui与平度αi对应的变化规律视为比例关系(线性关系),即μi=αi×[(Σαi-βr-τr)÷(Σαi)]。这样就把限度λ=λ0+Σμi视为行星的平黄经,也就是建部所谓的“非星之所当,作为平日之所当而算定之入历度数也”,它只是数学上的参变量而不具物理意义,由限度(入历度数,类于行星到近日点距离)计算行星的盈缩差y=f(λ)=[a±(b±cλ)λ]λ(λ为入历限数)。其算法思想是:引进参变量,把行星盈缩差计算方式转化成熟悉的日月盈缩差计算方式。
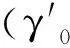
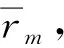
我们知道,求行星中心差应该以其平黄经(平度)入算,但这里的入历度分λ是由所谓的“限度”累计得到的,并非平度,所以五星盈缩差并不等价于西方的行星中心差。曲安京在文献[26]、唐泉在文献[15]中都曾指出,五星盈缩差既不等同于行星中心差,也与太阳中心差无关。
4 结 论
明代以后天文学家开始重视对法原的讨论,明末邢云路在《古今律历考》中企图恢复《授时历》的立法原理。西学东渐后伴随西法的东来与影响,中国历法开始编入历法原理。如,清初学者所编撰的《明史·大统历》,开篇“法原”首论推步原理;清代《历象考成》也是由“历理”“历法”两部分构成;清初学者黄宗羲(1610~1695)、黄鼎、梅文鼎(1633~1721)等人对《授时历》的历理多有阐发,但对其中如“白道交周”“五星推步”等问题,仍未能给出清晰的原理分析。江户时代日本学者对这些问题的注解工作,有助于我们对《授时历》五星推步算法原理的认识。
中国天文学家解决天体不均匀运动的计算问题,习惯于使用插值方法,但与太阳、月亮的非均匀运动现象不同,行星有退行现象,不能如日月那样直接由平黄经计算真黄经,从而引入了“限度”概念,将其转化为日月运动的算法模式,以解决数学计算上的困难,由此而造成其算法的复杂性。中西敬房及今人按照日躔、月离计算方式审视五星推步算法,自然因难以找到“限度”概念的物理解释而感到困扰。建部贤弘找出了限度与平度的关系,指出了“限度”的数学意义,从而揭示了五星推步算法的数学原理。其算法思想大致如下:
对五星的平黄经经过三次运动改正(五星盈缩差、距合差度、太阳盈缩差),逐步获得其真黄经。首先,将五星盈缩差看成是限度的函数,即平度(平黄经)的复合函数,通过插值方法获得第一次改正后的黄经值(平合定积定星);再根据五星与太阳的速度差获得“距合差度”这一修正值,修正退行时的黄经变化,以获得第二次改正后的黄经值(定合泛积);最后将太阳盈缩差看成是第一次改正后黄经(平合定积)的函数,也就是平黄经的复合函数,通过插值方法获得第三次改正后的黄经值(定合定积定星),也就是五星的真黄经。
这样的算法构造,体现了中国古代天文计算中的数值分析精神,如果硬要用“行星中心差”概念来描述中国古代行星运动改正的话,它实际是五星盈缩差、太阳盈缩差的叠加。
正是由于五星推步算法的建构以日月非均匀运动算法为参考、逐次构造复合函数来实现,才导致了行星视位置的计算精度远逊于太阳和月亮视位置的计算。对于五星推步算法的局限性,建部贤弘也有清晰的认识。他指出:
然有阴阳历出入纬度,又有上升下降之行,是等犹不能悉极尽其变,只依太阳求其经度,故验天时必非密也。然徒牵合术、空增损数,强求其合,故于术理不精,于立数不密。[25]
意思是说,在五星推步中,并没有考虑由纬度变化而导致的经度变化,只根据太阳运动来计算行星真黄经,必然存在很大的误差,其算法不过是“牵合”之术。
20世纪50年代以来,中外学者在讨论中国传统天文学中的日月五星运动时,习惯使用西方的同心球或椭圆模型的理论以及内插法、微积分等近代科学语言,对于日月运动,以此分析大体可以获得有效解释,但对于五星运动来说,以此来分析总会遇到一些困难。有鉴于此,中山茂提出中西传统科学“共轭不能性”的概念。“共轭”是一个数学概念,在数学中,如果两个角、线、点、图形、数等数学对象之间具有相互对称或相补的关系,通过代换其关系也不改变,就被称作是共轭关系。中山茂先生借用这一概念,意指中国传统科学与西方科学之间具有不可互通性。关于库恩的“不可通约性”(incommensurability)理论是一个争论已久的科学史方法论与科学哲学的问题,笔者这里不做讨论。当然,每个时代的历史研究,自然会使用特定时代的学术语言做出历史解释,我们应该采用什么样的语言来分析、解释西方文明以外的传统科学,值得深思与实践。

