水轮机磁悬浮导轴承动力学特性

李正贵，李 博，柴 芯，董国锋，刘小兵，杨逢瑜

(1.西华大学流体与动力工程教育部重点实验室，四川 成都 610039； 2.西华大学图书馆，四川 成都 610039；3.国际小水电中心，浙江 杭州 310002)

0 引 言

人们对占清洁能源比例85%水电的认识越来越理性，水电是环境友好能源。在国内，2014年水电装机容量历史性突破3 亿kW，成为节能减排主力军[1]。然而，水力发电设备运行中的轴承渗漏油，一直是一个无法彻底解决的难题，流域内污染城市用水的事故时有发生。另外这种轴承还存在抗冲击与抑振低、运行精度不高，承载力低等问题，而且水轮机启动过程低转速，也容易发生烧瓦现象。水轮机磁悬浮导轴承与传统轴承相比，不存在机械接触，转子可以运行到很高的转速，具有机械磨损小、能耗低、寿命长、无需润滑、无油污染等优点，故研制水轮机磁悬浮轴承装置必定是未来发展的一个方向[2]。

而磁悬浮导轴承存在永磁磁通密度较低，吸力小，磁力较弱，自稳定性差需控制器实时控制等问题，在理论上，还有一些科学问题尚待解决，国内外开展的一些研究也很有限。文献[3-5]为国内磁悬浮转子动力学相关的研究成果，文献[6-8]为日本、美国等的一些经典研究成果，文献[9,10]是透平机械领域磁悬浮轴承的应用，文献[11-13]是磁悬浮离心式磁悬浮泵、飞车风机及电磁阻尼方面的最新研究及论著，文献[14,15]是磁悬浮控制方面的最新研究成果，文献[29]是Dun Yueqin，Wang Xiuhe等提出转子混合磁轴承(HMB)。但是对于水轮机磁悬浮轴承的研究资料比较少见。基于大量文献，就水轮机磁悬浮导轴承结构设计及其力特性分析， 并对力特性进行有限元仿真，讨论了其动力学相关特性，为减小混合磁轴承磁力计算难度提供依据。

1 水轮机磁悬浮导轴承结构设计

1.1 水轮机磁悬浮轴承的构成

常规水轮机水导轴承，主要由水导瓦、固定油盆(上油箱)以及转动油盆等部件组成。水导瓦为分半筒式结构，瓦面材料为巴氏合金。轴承支架材料为铸钢，下法兰通常固定在顶盖上面，上法兰承受水导瓦压力。转动油盆在结构上为分半筒结构，材料为铸铝，油盆把合在分半卡环上，锁定在大轴上，卡槽沿轴向定位，销定位为径向固定，挡油护板分上、下两部分在水导瓦外侧，上部护板与转动油盆盖形成密封。

水轮机磁悬浮轴承在设计上也可按主动控制性、被动稳定性及混合性三种特性考虑，在自由度上通常为单轴到五轴，本文研究主轴两端4个径向自由度控制问题。水轮机为典型的立轴式机组，磁悬浮轴承在轴系结构中的设计为：推力轴承、上端磁悬浮轴承、主轴、下端磁悬浮轴承。

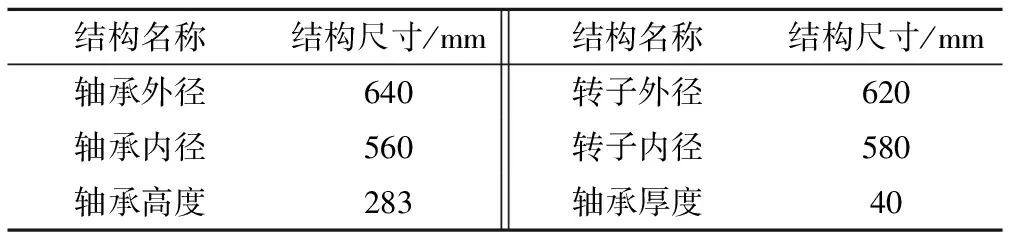
表1 磁悬浮轴承主要尺寸Tab.1 Magnetic suspension guide bearing principal dimension

如表1所示为磁轴承结构主要尺寸，图1为水轮机轴承结构示意图，图2为水轮机磁悬浮轴承纵向及横向剖面。本文选择的轴承为电磁控制加永磁偏置的组合形式，其中，轴向采用推力轴承支撑，径向为上下磁悬浮轴承支撑，磁悬浮轴承系统由外、内两部分构成，外侧为主动磁轴承，包括线圈和定子；内侧为Halbach阵列永磁磁轴承，中间为转子，转子部分由外磁环、隔磁部件和转子铁心组成。小扰动偏移可以由被动永磁轴承消除，扰动较大时，转子的位移由永磁磁轴承和电磁磁轴承共同控制，从而一定程度上降低了主动磁轴承功耗。

图1 水轮机轴承结构示意图Fig.1 Section of magnetic suspension bearing structure in turbine

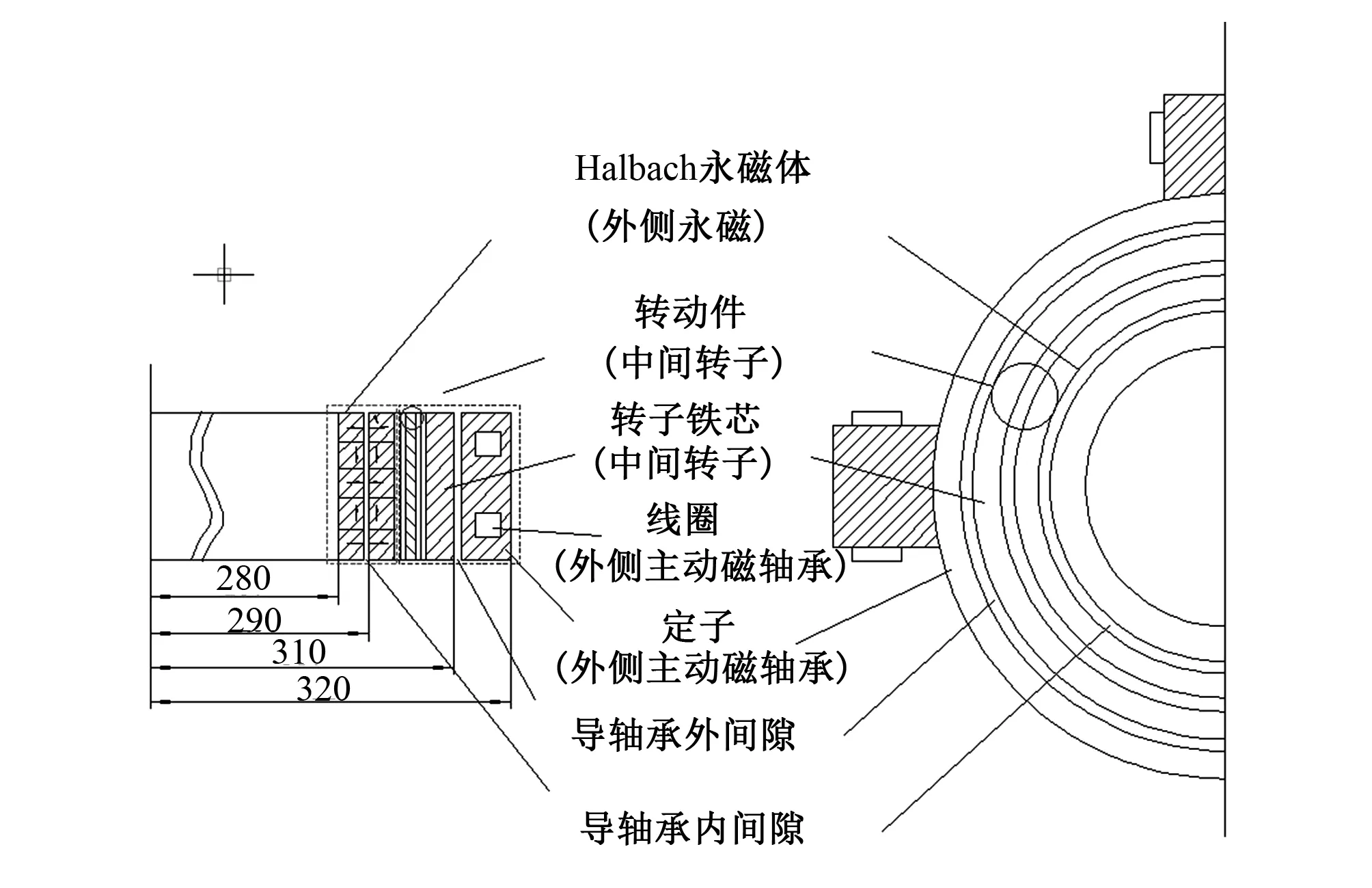
图2 水轮机磁悬浮轴承纵向及横向剖面Fig.2 Hydro-turbine magnetic suspension bearing longitudinal and transverse sections

1.2 磁悬浮轴承运动特性

对于水轮机磁悬浮轴承的研究主要针对本身运动特性和力特性，在水轮机稳态运行和瞬态过渡过程中，转动部分与静止部分总会产生一个动间隙Δ，如图3所示，在不同的运动角度，间隙位置与大小不同，在某一状态下，间隙分布情况见图4，其力学特性与Δ关系比较密切。

图3 不同位置间隙ΔFig.3 the air gap Δ in different location

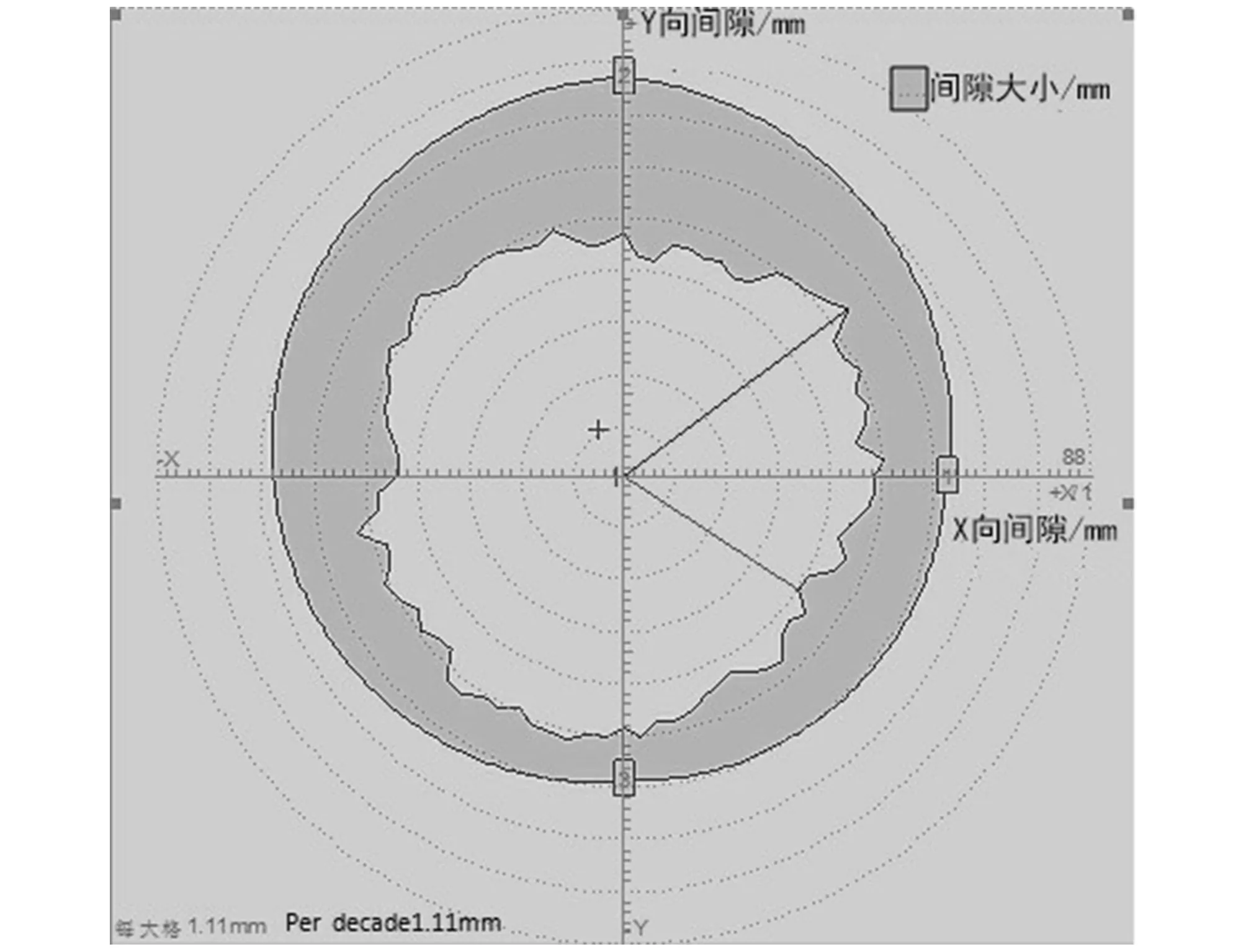
图4 某一状态下不平衡间隙分布Fig.4 Unbalance distribution of air gap in a certain condition

1.3 水轮机磁悬浮轴承受力控制特性

在静态工况下，由于永磁体力特性作用，水轮机大轴在对称位置，处于中心，磁力均匀平衡，以大轴中心作为坐标原点，在磁悬浮轴承径向正负方向上，动转子与轴承静止部分间隙相等，整个间隙间斥力均匀而且相等。

由于水轮机水力因素或发电机电磁因素影响，会在大轴上产生干扰，沿轴承径向负方向受到力F作用，大轴就会偏离中心位置而向径向负方向移动，产生一个Δ位移，形成不平衡磁拉力，这样磁悬浮斥力会发生变化，整个轴系受力发生变化，形成反方向合力。同时，由于水轮机磁悬浮轴承自稳定特性，控制系统检测到Δ值并产生反向磁拉力来平衡F，这样运行中大轴可以维持平衡；Δ大于设定阀值时，位移传感器以Δ转换成0～20 mA的电信号，通过电磁控制系统功率放大单元在相反方向线圈上产生相应磁场，产生磁拉力，并与Halbach阵列磁体产生的合力将大轴拉回平衡位置，实现水轮机轴承稳定悬浮。

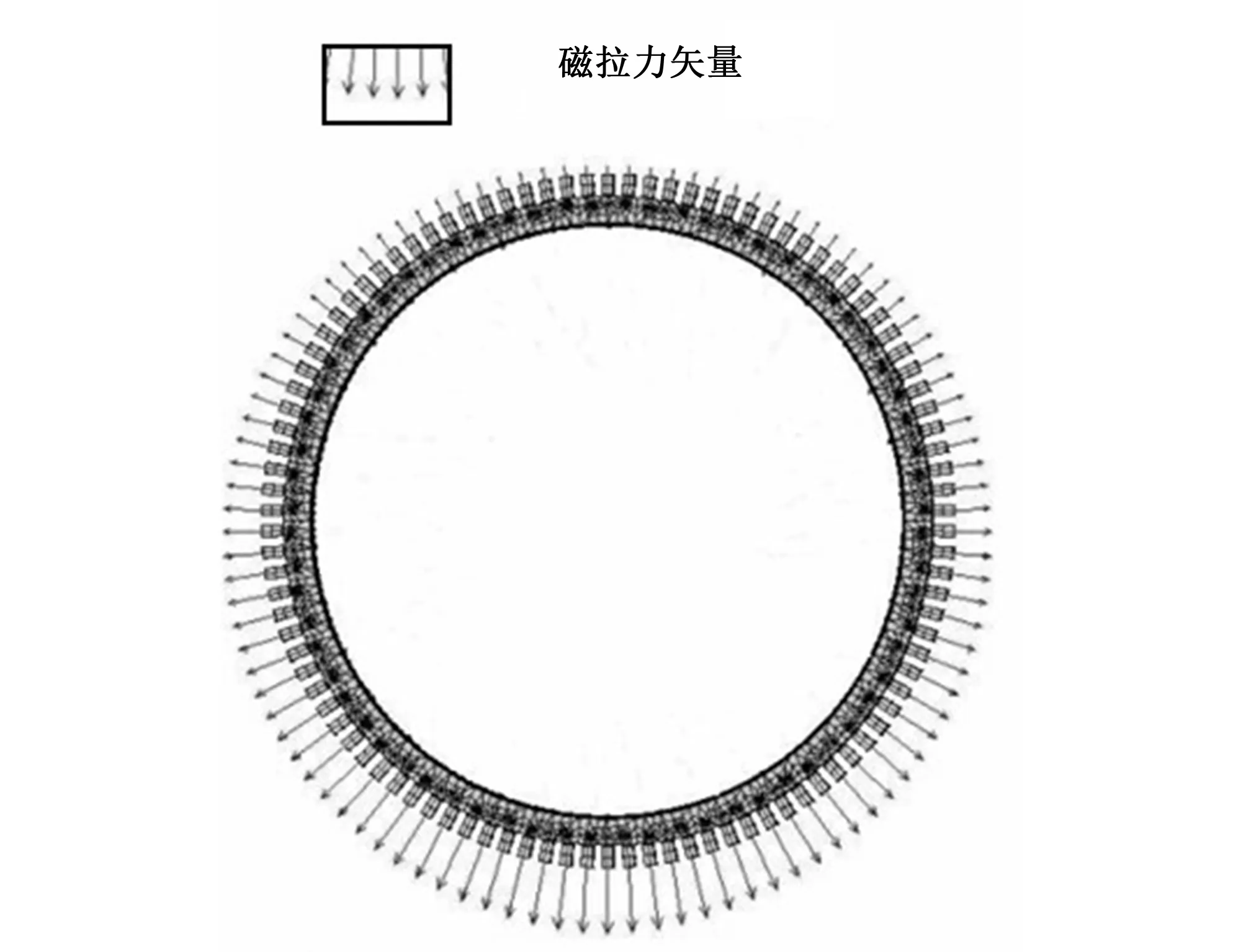
图5 在径向正方向侧较大Δ磁拉力分布 Fig.5 Distribution in the radial side larger Δ magnetic force

理论上讲，水轮机转子及轴系在发电机磁场及水轮机流场作用下悬浮，但实际上由于电磁、水力、机械原因，不可能悬浮在平衡状态，而是处于近似平衡状态，这种特性适用于由永磁及电磁作用下的混合轴承，二者可以协调工作，但永磁与电磁之间必须有隔磁部件隔离，同时，也要充分考虑水轮机比较大的承载力和刚度，而Halbach阵列永磁轴承轴向充磁或径向充磁符合这个特性，如图5所示，当发电机电磁及水轮机水力因素导致产生Δ时，需要对其间隙磁场加强，此时Halbach阵列的单边性可以减小Δ且产生较大的磁通密度，而增大Δ侧磁通密度则非常小，另外考虑到混合磁悬浮轴承的自稳性特性，在一定范围内Δ电磁轴承可以不工作，更符合节能优势。

2 水轮机磁悬浮轴承力特性分析

2.1 理论模型

在理论上，Halbach阵列力特性不能做到数学精确计算[17]。

图6 Halbach阵列磁体Fig.6 Halbach array magnets

图7 Halbach 阵列堆叠结构Fig.7 The stack structure of Halbach arry

图6为磁体沿y轴排列的Halbach阵列磁体，图中，dm是单元磁块的长度(y轴方向)，d为单位磁环高度。图7为Halbach阵列堆叠结构，为水轮机磁悬浮导轴承，属于径向结构，数学分析的基础为分子电流法，同时涉及到钕铁硼NdFeB材料的剩磁Br，一般不考虑横向端部效应，不计削弱侧磁力[18,19]。结合实际应用，在末端要增加一个长度为：dm(m+1)磁块，则加强侧的悬浮力Fz为：

(1)

式中：Fz为沿磁体加强侧悬浮力，N；Br为磁体剩磁，T；m为每个波长的单元磁块数；x为水平轴方向长度，mm；k为磁体波长数；d为单位磁环高度，mm；z为垂直方向悬浮高度，mm；λ为磁体波长，mm。式中空气磁导率μ0=4π×10-7H/m。

在计算中考虑曲率，设偏心距为u时，外环受径向力为：

(2)

式中：R为外磁环内侧半径，mm；r是内磁环外侧半径，mm；θ为偏心距矢径与转轴夹角；u为偏心距离，mm。

式中R2远远大于u2sin2θ，则-u2sin2θ≈0，另外，将cosθ等效函数化，则其显示解析计算方程为：

[12.5ku(e2.36ku+e-2.2ku)+9.87(e0.36ku-e-0.2ku)]

(3)

其线性化刚度为：

(4)

2.2 力特性分析

从式(3)可以看出，剩磁的平方与磁悬浮轴承径向磁力F0是成正比关系，其中波长λ、波长数k与dm(单位磁环高度)是一元函数关系，在研究中注重dm以及磁环厚度d对F0的影响。以五模块Halbach阵列水轮机磁悬浮轴承为研究对象，永磁轴承平衡间隙设为3.5 mm，dm=80 mm，波长λ=4，d=283 mm、内磁环外侧半径r=280 mm、外磁环内侧半径R=310 mm、剩磁Br=1.23 T、初始偏心距离u=2.1 mm，则得到d与F0特性曲线，如图8所示。

图8 磁环厚度d与径向磁力特性曲线Fig.8 The characteristic curve for the magnetic annulus thickness and radial magnetic forc

F0与d成非线性正比，磁环厚度较小时，其力特性变化为近似线性，随着磁环厚度增加，超过磁环厚度的40%～50%，F0逐渐由非线性趋于饱和，据此可以特性优化。

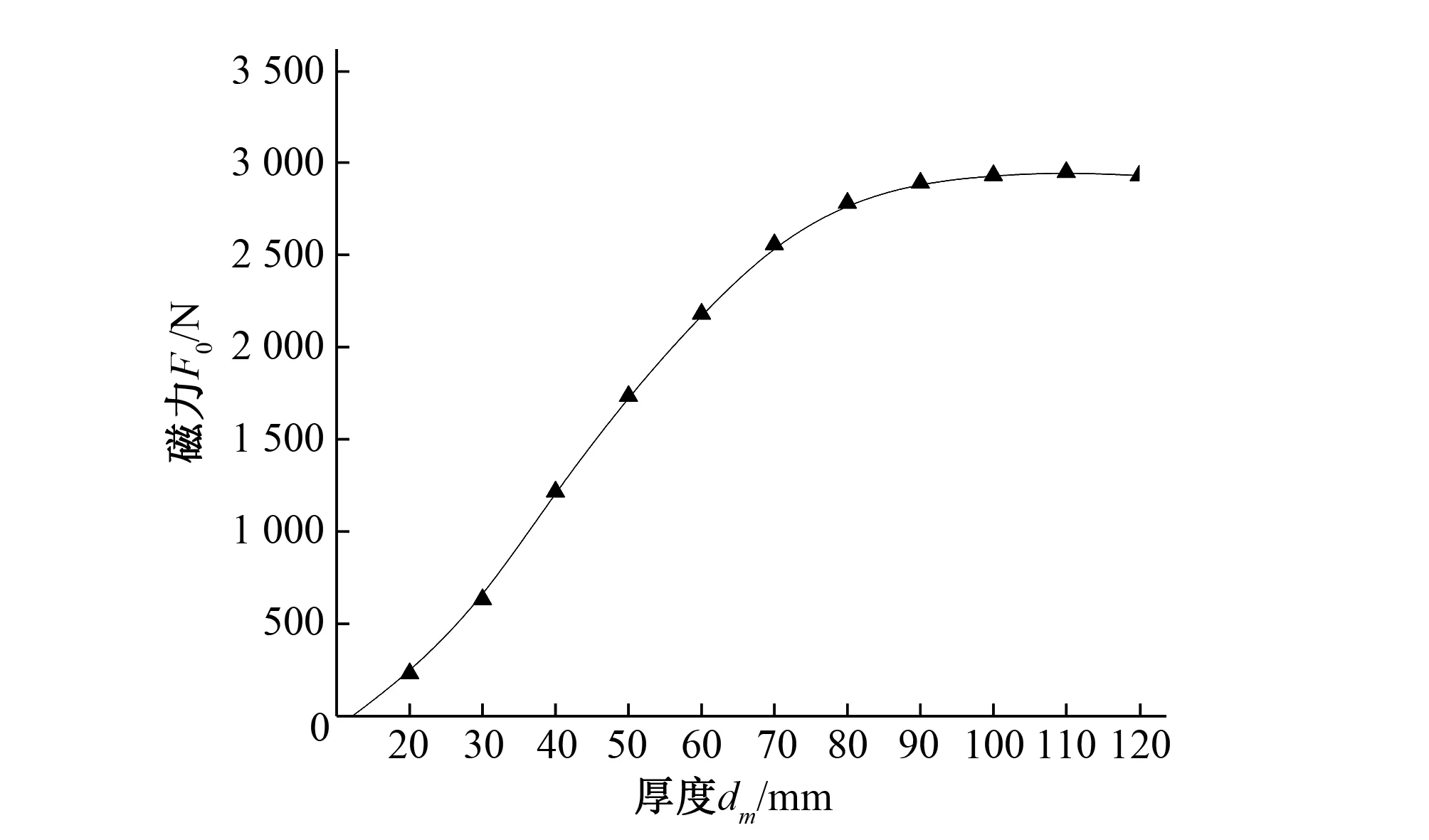
图9 磁环高度dm与径向磁力特性曲线Fig. 9 The characteristic curve for the magnetic annulus highly dm and radial magnetic force

由图9可以看出，dm的径向磁力力特性变化为近似线性，随着厚度增加，超过厚度约50%，F0逐渐由非线性趋于饱和，规律与F0与d特性相同。由以上分析可知，通过dm及d的力特性曲线，可以考虑水轮机磁悬浮轴承的结构优化设计。

3 力特性有限元仿真

本文参用CAD软件SOLIDWORKS进行三维建模，并用CAE软件ANSYS对前述理论结果进行仿真，结构参数：轴承外径D=640 mm，轴承内经d=560 mm，转子外径为620 mm，转子内径为580 mm，单磁极宽度为50 mm，悬浮间隙5 mm，磁材料NdFeB-N35SH，永磁环轴向长度h=283 mm，内、外永磁环径向厚度d=40 mm，永磁内、外环初始间隙δp=2.1 mm，线圈匝数为300匝，电流设定值为2.0 A，水轮机磁悬浮结构模型如图10。

图10 水轮机磁悬浮结构仿真模型Fig.10 The simulation model of the magnetic suspension structure of the hydro-turbine

如图11所示，由磁悬浮轴承磁力线密度分布规律及磁悬浮轴承磁通密度分布规律发现,磁感应强度在水轮机转轴的水导轴承部位，与磁铁最近距离处产生较大数值，故在同一处的磁场强度较大,在磁通不发生饱和时,磁通密度最大部位磁力最强，在自由度上，水轮机径向混合磁悬浮导轴承具备磁通密度分布规律，是自稳定特性的理论基础。

图11 水轮机磁悬浮磁通密度分布Fig.11 magnetic suspension magnetic flux density distribution of hydro-turbine

由数学分析可知，水轮机磁悬浮轴承系统模型中存在有复杂非线性关系，很难直接用它去分析系统的特性。但是通过Ansys计算，如图13，其磁力特性与间隙之间关系很明确，从图中可以看出，间隙越小、对应的磁力越大，使轴承具备自稳定特性，同时其负刚度可以通过轴承永磁特性调节。

图12 数值仿真与计算磁力曲线比较Fig.12 Comparison curves for Numerical simulation and calculating magnetic

图13 磁力特性与间隙的关系Fig.13 Relations between the air gap and magnetic characteristics

4 结 论

研究发现水轮机永磁和电磁混合Halbach阵列结构磁悬浮轴承，在单一自由度上具备自稳定特性，其负刚度可以通过轴承永磁特性调节。小扰动偏移可以由被动永磁轴承消除，扰动较大时，转子的位移由永磁磁轴承和电磁磁轴承共同控制，从而一定程度上降低了主动磁轴承功耗。该研究结论为水轮机径向磁悬浮导轴承装置在工程应用中提供一定指导，为减小混合磁轴承磁力计算难度提供支持。