基于相移法的三维重建减噪算法研究

庄 一,石 岩,汪诗宇

(中国计量大学 光学与电子科技学院,浙江 杭州 310018)

三维测量技术作为高新技术[1],近年来,随着相关计算机处理技术、图像处理以及光电子测量等技术不断成熟,三维测量技术得到迅速的发展,在国防安全、先进制造、医疗诊断等领域有广泛的运用[2].目前,在相关产品的研发方面,德国处于领先地位,拥有许多在工业等领域的三维测量设备.国内主要有清华大学的北京田园三维科技有限公司等研制相关的条纹三维测量设备[4].目前测量物体三维重建的主要技术难点有以下几个方面:投射条纹的产生及投影,系统标定,折叠相位[4]展开以及噪声的影响.其中噪声主要来源于器件的固有噪声与投影光栅条纹不均匀带来的噪声[3].器件的噪声主要通过更换不同的器件降低噪声,但是浪费时间并增加了成本;投射条纹不均匀导致的噪声,常用的是对提取的相位图进行中值滤波等常规算法,但这样容易改变被测物体的三维信息,导致被测物体的三维信息不精确.也有许多提出利用编码的算法替换之前的正弦条纹,利用编码结构光[8]算法比较复杂,对于硬件的条件也比较高.

本文提出了一种基于相移法的三维重建降低噪声的算法,通过对采集变形条纹图进行减噪处理,从而降低被测物体受光照不均带来的误差.算法主要分为三步:第一步,用四步相移法得到被测物体的相位图;第二步,用Sobel边缘检测算子[9-10],人工设置合适的阈值,自动检测出被测物体相位图中噪声区域;第三步,通过提取噪声点,依次提取并且判断该噪声点四个方向每个像素点是否在没有噪声区域内,保存其数据,通过均值替换该噪声点,从而提高重建物体的精确度,减少噪声.

1 消除噪声算法设计

1.1 四步相移法提取相位

相移法[10-11]的主要原理是利用多幅光栅条纹图像来获得被测物体相位.如果投射的条纹是正弦,分N次投影在待测物体上,那么两幅相邻的正弦条纹的相位差值为2π/N,令In代表第n(n=1…N)幅图像光强[13-14].

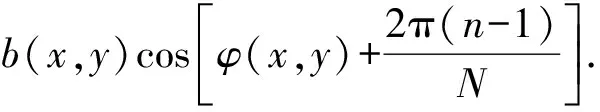
(1)

式(1)中:ɑ(x,y)代表背景光的强度,b(x,y)为被测物体的反射率,φ(x,y)表示的是物体高度相关的调制相位[15].

四步相移法是当N=4时,即投影四幅光栅条纹图时,四幅光栅条纹的光强为:

(2)

对应的相位的求解公式如下:

(3)

通过提取参考面无物体的时候条纹相位为φ1(x,y)和放置物体后的条纹的相位分布φ2(x,y)可通过式(4)得到.这样,待测物体所形成的相位差为

Δφ(x,y)=φ2(x,y)-φ1(x,y).

(4)

最后,通过利用所求的相位差与高度的关系求出待测物体的深度,如图1.

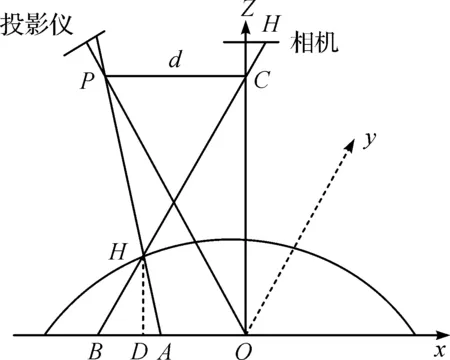
图1 交叉光轴系统原理示意图Figure 1 Geometry of crossed-optical-axes system

图1中OP是投影系统透镜的光轴,它与成像透镜的光轴OC相交于点O,其中Ox是所在的参考平面,P和C点分别是投影透镜于成像透镜的入瞳中心,两点的距离为d,距离参考平面的距离为l,通过投影仪将光栅投射至物体的表面点H,H成像在成像面上H’.PH与参考平面Ox相交于点A,CH与参考平面相交于点B,两点之间距离为s(x,y),而物体表面点H距离参考平面的深度为h(x,y),通过三角形PHC于三角形BHA相似可得式(5):

(5)

实验中投射的是正弦光栅条纹,则参考面和物体表面上各点的光强可分别表示为I0(x,y)和I(x,y),即:

I0(x,y)=a(x,y)+b(x,y)cos[2πf0x+φ0(x,y)];

I(x,y)=a(x,y)+b(x,y)cos[2πf0x+φ(x,y)].

(6)

式(6)中:a(x,y)代表背景光的强度,b(x,y)为被测物体的反射率,φ0(x,y)和φ(x,y)分别对应为参考面和被测物体表面的相位信息.可以证明AB两点之间的距离s(x,y)和式(4)求得相位差Δφ(x,y)有以下的关系:

Δφ(x,y)=2πf0s(x,y).

(7)

式(7)中的f0=1/p是投影到参考面上的光栅条纹的频率,将式(7)代入式(5)中可得

(8)

通过式(8)可知,只要得到物体表面与参考面的相位差Δφ(x,y)则可计算出物体的深度值,实现三位轮廓重建.

1.2 提取噪声区域

通过投射光栅条纹至被测物体,装置如图2.

图2 装置示意图Figure 2 Schematic diagram of installation

图2中,(a)图是用到的Sony投影设备,摄像设备是基于Kinect2.0.通过投影仪将光栅投影在物体上,光栅的频率(f)为1/64,通过测量,投影设备与摄像设备的水平距离为12 cm,投影设备距离参考面距离(l)为80 cm.物体背景墙面导致投射的光不均匀,产生噪声,产生“拉线”现象,用相机采集被测物体上的条纹信息有差异,如图(b)中长方形框中标记所示,重建误差较大.因此,对采集条纹信息进行边缘检测处理.

(9)

式(9)中A代表图3(a)所示,图像中的物体是一个纸杯子,横纵坐标是其像素值范围,由于贴在背景墙上,墙上的不均匀导致采集的光栅信息有误差,Gx以及Gy分别为Image1通过水平和垂直的检测后图像,图像中的梯度大小为上述经过水平和垂直检测后图像通过式(6)相结合得出梯度:

(10)

人工选择合适的阈值,如图3(b)是对采集的图像(a)利用相移法,提取出的相位信息图,从图中可以清晰知道,噪声区域,正常区域,背景区域有很大的区别,当设置阈值在-1至0之间,当(10)式求得每个像素在设定阈值之内,将该点像素值设置为某一特定数值(本文为了实验明显设置为0),不在阈值的设置为255.这样能清晰看出待测物体轮廓信息以及噪声的信息,如图3(c);当设置阈值为-4,当低于该设置的阈值,将其像素设置为255,高于设置为0,能很好提取受影响的区域,如图3(d)中长方形框中标记区域.

1.3 噪声区域的消除

图3(b)中白色区域是自动识别的噪声区域,将大于阈值的像素值设置为特定数值即噪声区域的像素值,逐点判断每行像素值,如果该像素值为设置的特定数值,则认定为噪声点,如图3.

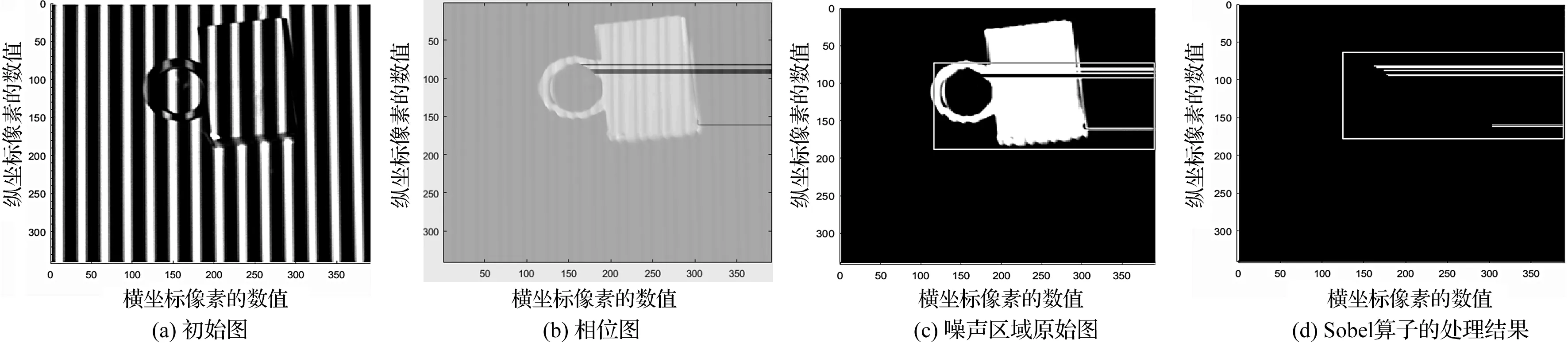
图3 提取噪声示意图Figure 3 Schematic diagram of noise extraction

当由上述算法找到该噪声点,提取该点的行和列没有噪声影响的物体的像素值,对提取的噪声点的邻域取均值,算法模型如图4.

图4 提取噪声点流程图Figure 4 Flow chart for extracting noise points

A(i,j)B(i,j)Image(i,j)D(i,j)C(i,j)

图5替代噪声点路径

Figure 5 Alternative noise point path

图5中Image(i,j)表示噪声区域的随机噪声点,提取除该点以外的四个方向的像素值,然后进行判断是否在没有受光照影响物体像素值范围内,提取完四个方向在该范围内的像素值,对其取均值赋值给Image(i,j),实现该算法的流程图如图6.

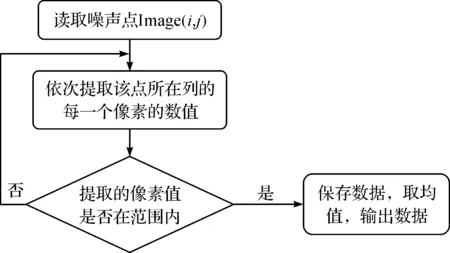
图6 替代噪声点算法流程图Figure 6 Flow chart of alternative noise point algorithm

通过上述流程图逐点将噪声点消除,图7(a)中的纸杯子是受噪声影响的原图,图7(b)是通过传统的中值滤波算法处理后的图,图7(c)是利用高斯滤波处理后的图,图7(d)是本文提出的算法效果图.

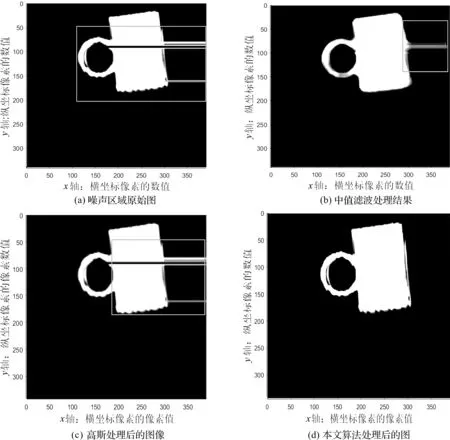
图7 算法处理前后示意图Figure 7 Schematic diagram before and after processing by using algorithm

通过比较,中值滤波的滤波效果并不能完全消除噪声带来的影响,如图长方形框中标记地方,只是将整个区域均匀,而噪声区域并没有因此而完全消除;而高斯滤波效果不是很好,与原始图像比较,并没有太大的改善,相比较而言,本文提出的算法能很好地消除噪声,还原物体的整个三维轮廓.

如图8(a)和8(b)是通过算法前后的三维重建图,如图中长方形框中标记所示,利用上述所说的算法能很好地消除噪声的影响,提高待测物体的还原度.

图8 模块三维重建示意图Figure 8 Schematic diagram of 3D reconstruction module

2 实验

为了进一步检验本文提出算法的正确性,在实验室采用四步相移法对一个标准模块进行测量,并采用本文所提出的噪声处理.本次实验中摄像机和投影仪分辨率都为1 024×768.摄像机与投影仪的位置与待测物体距离为1.2 m,通过投影仪将具有相位差的条纹投射在待测的模块表面,摄像机采集变形的光栅条纹图像.

图9(a)是测量模块实验装置图,图9(b)是实验的模块,所使用的模块是规则的长方体与正方体,长方体的高度与正方体的高度分别为1.5 cm与6 cm.

图9 模块装置示意图Figure 9 Schematic diagram of module device

如图10(a),是通过摄像机采集的原图,由于投影光栅照射在模块,光栅在墙面上不均匀,导致在模块周围会出现噪声区域,如图10(b)框中标记所示,框中的区域高度会出现11.06 cm的错误数值,从而影响物体的重建.

图10 模块三维重建示意图Figure 10 Schematic diagram of 3D reconstruction module

通过利用中值滤波,高斯滤波方法去除由光照不均匀带来的噪声,如图11(a)和(b).

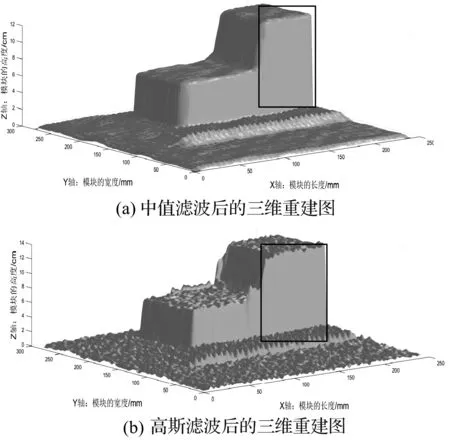
图11 传统算法去除噪声后三维重建图Figure 11 3-D reconstruction diagram of removing noise by the traditional algorithm

通过图11(a)和(b),中值滤波只能将整个重建图变均匀,但没有去除噪声区域,导致重建的立方体多了一部分,如图框中标记的区域.图12是利用本文所提出的算法对噪声区域进行处理的结果.

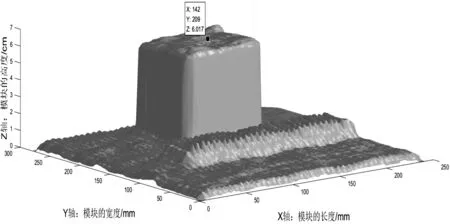
图12 本论文算法去除噪声后三维重建图Figure 12 3-D reconstruction diagram of removing noise by the proposed algorithm

通过图12重建结果与传统算法重建结果相比较起来,本文提出的算法不仅能很好地还原物体三维信息,而且能很好地消除由光照不均匀带来的误差区域.

在图13重建的三维图中随机选取8个点的坐标数值,如表1.

图13 本论文算法去除噪声后三维重建图Figure 13 3-D reconstruction diagram of removing noise by the proposed algorithm

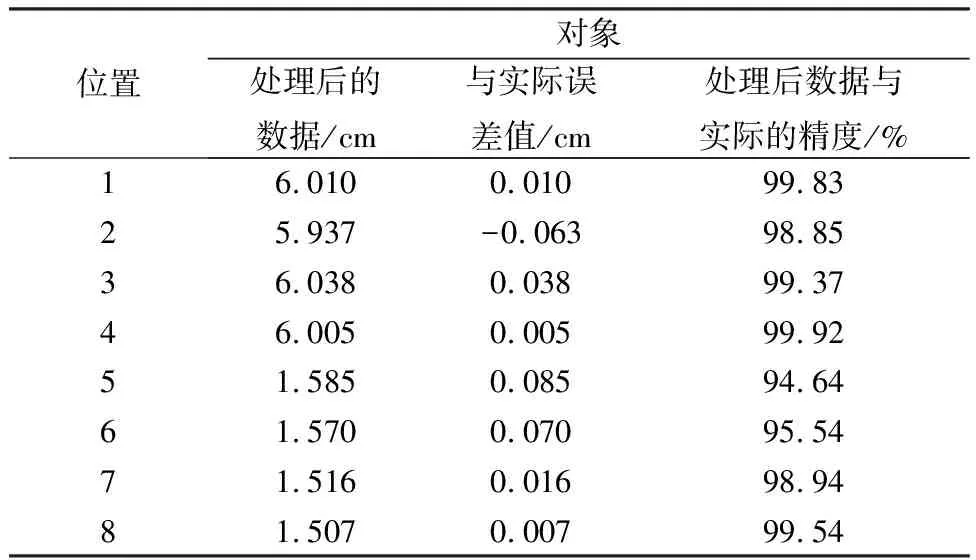
表1 绝对误差表

表1中可以看出受处理后的模块数据的与实际的误差值相差很小,所达到的精度很高,能很好解决光照不均匀带来的影响.对上述随机取的精度值取个均值,处理后的数据与实际数据精度为98.32%.

3 结语

通过上文中的实验结果,文中设计的减噪算法结合四步相移法有明显的效果，如图3(b).由于光照的不均匀,导致其重建的模块与原物有很大的区别，如图7.对噪声区域利用传统的降噪算法,虽然能减少部分噪声影响,但不能完全消除噪声的区域,如图8.本文提出的算法能很好还原待测物体的三维信息,测量精度达到98.32%,取得了很好的工程效果.但是,所设计的算法还有很多改进的地方,比如当检测复杂物体时该如何进行噪声消除等.