基于材料特性的飞刀铣削加工表面粗糙度模型的研究
(北京工业大学 机械工程与应用电子技术学院,北京 100124)
0 引言
金刚石飞刀铣削加工对于制造各种工业领域的精密零件非常重要,如光学、清洁能源、信息工程和通信技术等[1,2]。众所周知,这种加工技术能够加工出超光滑的表面,通常不需要抛光工艺。但是,这种优异的加工性能强烈依赖于加工环境,机床性能,工艺参数,刀具几何形状及工件材料特性[1,3]。而在众多的研究中,工件材料特性的研究是一个盲点,值的去深入探究。
在超精密飞刀铣削加工技术中,加工精度已达到纳米级,以往在传统研究方法中被忽视的工件材料特性对表面质量的影响将不能被忽略。通过对材料应力应变特性的研究发现,在挤压和去除的作用下,材料会出现弹性回弹和塑性侧流的现象,而这些现象的发生都与材料自身的性能有密切关系[4]。工件表面出现回弹和侧流的现象,会对工件的表面形貌和表面粗糙度值产生影响,而对表面形貌预测模型的研究下一步的趋势是基于材料特性的综合模型的研究[5]。本文将研究在飞刀铣削加工KDP晶体加工过程中,材料的特性对表面粗糙度值的影响。
1 材料回弹对表面粗糙度的影响
在回转加工过程中,由于刀尖形状,进给速度,切削深度和转速等因素的共同影响下所产生的误差为运动学误差,切削由文献[6]得:
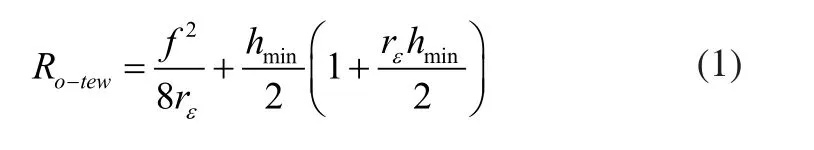
式中Ro-tew为表面粗擦度值,f为进给速度,rε刀尖半径,hmin最小未变形切削厚度。
由于在加工过程中,在切削力的作用下刀具会对工件材料产生挤压,切削原理如图1所示。如图2所示,在切削力消除后工件材料由于自身的力学性能,会产生弹性回弹。由于材料自身的力学性能,材料的回弹现象经常会出现在加工工件的表面。特在超精密回转加工过程中,加工精度已达到纳米级,虽然材料回弹现象不是非常明显,但在纳米级精度下,对工件表面粗糙值的影响非常大,研究材料回弹对工件表面质量的影响具有十分重要的意义。
1.1 切屑形成机理分析
超精密飞刀铣削加工是一种具有纳米级别加工精度的加工方式,所以其切削模型属于微观切削模型。通过分析飞刀铣削的加工方式和加工机理可得到材料去除过程的模型,如图1所示。飞刀铣削加工的加工方式为回转运动和直线进给运动的耦合加工方式,即刀具随主轴进行回转运动的同时,吸附在真空吸盘上的工件会随着导轨进行直线进给。刀尖每次回转都会在工件留下刀尖轨迹,相邻两条刀尖轨迹的距离为每转一圈进给速度的距离。在工作时,由于刀尖为圆弧型,所以切削刃在切除材料时,从刀尖到未加工工件表面的位置的这段切削刃所切削的厚度也是不同的。当切削厚度大于最小未变形切屑厚度时,材料与工件材料发生分离,产生切屑。由于材料的最小未变形厚度远远小于工件加工时的切削深度,所以在相同的加工参数条件下材料的弹性回弹量为定值。

图1 飞刀铣削加工中切屑形成分析
1.2 材料回弹引起的形变量
为计算材料的回弹引起的形变量,根据文献[7],建立考虑了工件硬度和杨氏模量的模型:

式中H为工件材料的硬度;s材料回弹量;rn刀具切削刃半径;k为工件材料和刀具形状相关的参数。

图2 材料回弹现象示意图
通过以上分析可得:在微米级加工中,如果未变形的切屑厚度小于临界值或所谓的最小切屑厚度,材料只发生弹性变形,刀具挤压过后,材料弹性恢复,则不会形成切屑。当切削厚度接近临界最小未变形切削厚度时,此时的变形包含塑性变形和弹性变形,弹性变形下刀尖划过工件后会产生弹性回弹,塑性变形的不会恢复。当切削厚度大于最小未变形切削厚度时,工件表面只产生塑性变形。当切削厚度继续增加时,切屑就会产生断裂破坏,此时的工件表面会出现断裂等现象。所以在研究材料回弹现象时,关键是找到最小切削未变形切削厚度。
通过文献[4]获得金刚石回转加工中最小未变形切屑厚度hmin与切削刃半径rn之间的关系:

式中c的范围为0.3~0.4。本文取0.3。
通过式(1)和式(2),两个式子中均有切削刃半径rn,所以通过这两个式子我们可以建立s和hmin之间的关系。从而建立一个关于s和hmin之间的压力模型。
在本文研究中,假设认定KDP晶体是具有良好弹塑性材料,由文献[8]可得到表1中KDP晶体材料的特性参数,相关量采用的是平均值,如表1所示。

表1 KDP晶体材料性质
根据表1中KDP晶体的参数,可以计算出,该材料的弹性回弹量如下式:

2 塑性侧流对表面质量的影响

图3 材料侧流对工件表面粗糙度影响的示意图
2.1 材料侧流的形成机理
本文提出了描述塑性流动形成的物理模型,如图3所示。图中假设塑性侧流的形成主要取决于未去除的材料。由图3可以看出,最小未变形切屑厚度hmin和有效切削宽度bD,即活动切削刃AB的弧长,对塑性侧流的形成起着至关重要的作用。对于厚度小于hmin的未去除材料,绿色阴影面积大约等于hmin和bD的乘积,它们将被刀具侧面挤压和摩擦,而不是在刀具切削刃之前累积以形成切屑。刀具挤压和摩擦后,材料回弹发生在工具标记的底部,根据前文中的弹塑性理论,可以更好的建模。
2.2 侧流引起的形变量建模
然而,在刀具挤压和摩擦过程中,应力集中不可避免地发生在活动切削刃的前方。为了释放集中应力,受到挤压和摩擦的材料将流向活动切削刃的侧面,即如图3所示的A点和B点,最终形成塑性流动。对于在B点累积的材料,它们可以在下一次切割中被去除,其效果在本工作中不予考虑。然而,作为表面粗糙度的重要组成部分,A点的材料积累将在理论上建模。加工过程中低进给速度和小刀尖半径是形成塑性侧流的首选条件,因为切削刃前面的应力集中[4]。因此,A点的塑性流动的表达式:
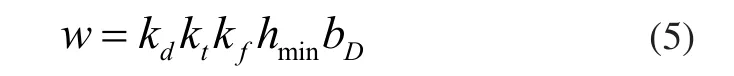
式中w为塑性侧流形变量,kd为与工件材料相关的一个系数,本文中取值为0.001μ m-1,kt为与刀尖半径相关的一个可变系数;kf为与刀具进给速度相关的可变系数,bD为有效切削宽度。
kt随着刀尖半径的减小而增加。这是因为刀尖半径的减小将导致切削刃前的应力集中增强,从而促进塑性侧向流动。因此,提出了线性函数来模拟刀尖半径的影响,其描述如下:

其中rε-ref是指定参考刀具的刀尖半径,在本文中选取933.6μ m。k1和k2是依赖于参考刀具的刀尖半径的拟合常数。根据经验公式拟合可得:k1和k2分别为0.26791和0.71772。应该指出的是,对于这些参考工具的选择,它仅用于通过拟合分析确定常数k1和k2。
进给速率的减小增强了活动切削刃前面的应力集中,使得kf的缓慢增大。因此,提出了指数和二次耦合函数来描述进给速率的影响。

其中A、B和C是拟合系数。实验观察经验总结结果表明,这三个系数分别是0.01502,0.00353和2.67788。
工件的有效切削宽度[9]:

3 工件材料特性对工件表面粗糙度的影响分析
结合上文中的分析,可以建立基于工件材料特性的表面粗糙度模型[10],如图4所示。

式中Rth为基于工件材料特性建立的表面粗糙度模型的表面粗糙度值。

图4 工件表面粗糙度模型示意图
4 实验验证及结果分析
4.1 实验设置
实验机床选用专用KDP晶体飞刀加工机床。实验参数选用切削深度选取5μ m。进给速度选择1μ m/r、2μ m/r、4μ m/r、6μ m/r、8μm/r和10μm/r共计六组。
刀具参数:刀尖半径为1830.4μm,前角0°,后角10°,平均切削刃半径为52.8nm。
实验方法:在切削深度一定的条件下,以不同的进给速度进行切削加工。
4.2 数据处理和分析
对实验获得的工件表面,进行多点采样,提取同一平面上不同位置的表面数据,然后通过Veeco旗下的WYO软件进行数据处理,可以获得工件表面采样点的三维形貌,二维表面图和表面粗糙度值等数据。
同时为了更好的表达模型的预测精度,定义残余误差:实验测量值和模型计算值的差值即:

式中tε为残余误差;Rt-m为实验测量结果;Rth为模型预测结果。
残余误差与测量值之间的比值为预测误差η:

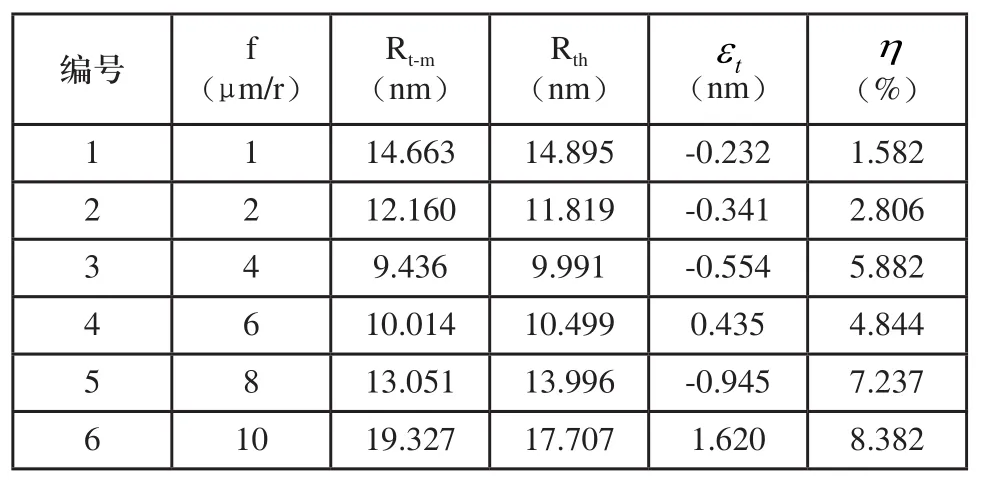
表2 实验结果与预测结果对比表
由上表对比结果可以说明:飞刀铣削加工方式具有较高的加工精度加工进度达到纳米级别,最好表面粗糙度值达到9.436nm。残余误差控制在-1nm~2nm之间。预测误差范围控制在8.382%以内,同时最高精度为1.582%。说明该预测模型具有良好的预测精度。
5 结论
1)本文在基于现有研究的基础上,将最小未变形切屑厚度引入到KDP晶体加工研究中,同时分析了材料才加工过程中材料回弹和测流对工件表面的影响。通过结果对比可得出,该基于加工原理和材料力学性能的研究具有较高的可行性,同时为研究工件材料对工件表面形貌的影响的提供了新的思路。
2)本文将材料属性作为主要因素,研究其对工件表面粗糙度值的影响,同时在此基础上建立了表面粗糙度模型,通过验证实验,可得出该模型具有良好的预测精度,误差范围控制在8.382%以内,同时最高精度为1.582%。最好表面粗糙度值为9.436nm。良好的预测模型可以在未加工条件下,获得工件的表面形貌预测值,同时也可获得最优的加工参数,提高加工效率。

