修正WRF次网格地形方案及其对风速模拟的影响
刘郁珏 苗世光* 刘 磊 胡 非3)
1)(中国气象局北京城市气象研究所, 北京 100089)2)(中国科学院大气物理研究所大气边界层物理与大气化学国家重点实验室, 北京 100029)3)(中国科学院大学, 北京 100049)
引 言
我国风能资源非常丰富,了解风场信息是风能开发利用的关键前提。朱蓉等[1]指出有效的风能资源评估技术是数值模拟技术与适当的测风塔观测相结合的方法,因此,需要进行高分辨率风能资源分布研究[2-3],尤其是气象站分布稀疏地区。但影响风场因素很多,其中地形具有重要作用[4]。复杂地形区域的风资源评估常利用数值模拟手段,其模拟准确性一直是风能预报的难点和重点[5-7]。而我国超过2/3的土地属于山地,地形和地表特征复杂。中尺度数值预报模式WRF(Weather Research and Fore- casting)[8]是目前风能评估中应用最广泛的中小尺度天气数值模式之一。WRF常用于直接模拟获得天气尺度背景风场,或与计算流体力学类模式进行离线耦合开展中-微尺度风场模拟,并已在全国各地得到应用[9-16]。由于计算流体力学模式不考虑大气物理过程,在应用上仍受很大限制。随着计算机性能逐渐提升,跨越“灰区尺度”[17]直接利用WRF开展全物理方案的微尺度高分辨率风场模拟已成为新趋势[18]。
但陆续有研究指出,当模拟区域地形复杂崎岖时,WRF对近地面风速模拟存在较大系统性偏差,呈现出平原、山谷及风速较小地区模拟风速的高估,山腰、山顶地区风速低估现象[18-24]。针对这一问题,Jiménez等[25-26]通过在欧洲西南部的伊比利亚半岛开展密集风速观测试验,对WRF的低层风速模拟进行了全面检验。不仅证实系统性误差的存在,还指出误差源于WRF在模拟大气运动时对地形进行平滑处理,而忽略了次网格地形作用影响所致,尤其是平原等小风速地区。为弥补次网格地形带来的影响,Jiménez等[26]提出一种次网格地形方案,即Jiménez次网格地形方案(以下简称Jiménez方案)。
结果表明:该方案能有效减小山谷、平原风速,也能部分提高山顶风速,使近地面风速模拟更准确,并已加入WRF3.4以上版本的YSU边界层方案中。国内学者分别在京津冀太行山脉、黄土高原、云贵高原等复杂地形区域中尺度分辨率下验证了Jiménez方案[27-29],结果显示:方案对WRF的系统性偏差有明显修正效果,能更好描述风速的空间分布特征。
但当模式分辨率提高后Jiménez方案出现失效情况,尤其是高分辨率中-微尺度的山顶地区修正结果明显错误。推测可能是因为原始Jiménez方案在设计之初只依据美国区域低水平分辨率地形资料,且只重点关注了平原、山谷等小风速地区,并未考虑模式网格水平分辨率及方案对山顶大风速区的影响。为证实猜想,本文选取京津冀西部太行山复杂地形区域进行系列模拟试验,基于高精度地形高程数据对原始Jiménez方案进行分析,找出原因并修正方案;同时利用自动气象站实测风速检验修正前后的模拟效果。结果表明:在复杂地形区域开展风场模拟时,不同分辨率下需谨慎开启Jiménez方案,而修正后的Jiménez方案可供参考。
1 研究区域及模式试验设计
1.1 研究区域及观测试验
北京市位于华北平原北部,地形复杂,其北、西北方向背靠燕山山脉和太行山脉,南、东南方向由山地逐渐过渡为平原。北京地区低层大气不仅受山谷风、城市热岛环流的相互作用,还受海陆风环流影响。其西北山区一带风能蕴藏极为丰富,建造有北京官厅风电场,其西北部为河北省张家口市,曾被誉为“风电第一市”。为分析Jiménez方案在不同分辨率下的效果,本文模拟区域选取北京西北部山区(如图1黑框所示,大小64 km×51 km),并着重分析模拟区域内的小海坨山局地区域(图1和图3蓝框所示,大小7 km×5 km)。通常山区自动气象站很少且海拔较低,分布相对稀疏,周边地形相对平坦。而北京城市气象研究所承担的冬季复杂地形气象观测试验项目MOUNTAOM(MOUNtain Terrain Atmospheric Observations and Modeling)在小海坨山的山顶、山谷均设有自动气象站(图2),采样周期为10 min。其中,小海坨站位于山顶(40°33′15″N,115°49′45″E,海拔2108 m);二海陀站位于山腰(40°32′36″N,115°49′10″E,海拔1805 m);西大庄科站位于南部,其北、东、西三面环山,西大庄科站位于两条峡谷交界处(40°31′13″N,115°46′57″E,海拔900 m)。由于地形十分复杂,在同一个山体建立多个自动气象站试验较少,数据宝贵,对本文分析次网格地形方案处理高精度地形及评估方案非常有利。

图1 模拟区域和分析区域(填色为地形高度)(黑框为模拟范围,蓝框为小海坨山所在区域)Fig.1 Computational and analytical domains with the terrain elevation(the shadeded denotes terrain)(black frame denotes simulation domain, blue frame denotes Xiaohaituo mountain)

图2 小海坨山地形(填色)(黑色圆点为自动气象站)Fig.2 Analytical domain for Xiaohaituo Mountain(the shaded)(black dots denote automatic weather stations)
1.2 模拟试验基本设置
模拟区域位于北京市延庆区西北部与河北省交界处,既包含小海坨山所在军都山山系,也包含延怀河谷,是研究复杂地形对风速影响的一个具有代表性的局地区域。
模式初始场和侧边界条件来自北京市气象局数值预报业务系统RMAPS-ST(睿图快速更新多尺度分析和预报系统-短时预报子系统)。其D2模拟区域预报起始时刻的预报分析场,分辨率为3 km×3 km。RMAPS-ST前身为BJ-RUC V2.0[30],预报分析场同化了GTS常规资料(探空、地面和飞机报)、北京地区自动气象站以及全国地基GPSZTD数据,RMAPS-ST D2区域还同化了京津冀区域7部雷达径向风和29部雷达组网拼图数据。其中,用于径向风同化的京津冀7部雷达包括5部S波段和2部C波段雷达。29部雷达是RMAPS-ST 3 km 区域范围内的天气雷达,包括S波段和C波段雷达。雷达拼图数据是通过一种或多种客观分析方法将来自多部雷达的反射率因子插值到统一的笛卡尔坐标后,将来自多个雷达的格点反射率因子拼接形成3D雷达拼图。由于RMAPS-ST同化了多种本地观测,较美国国家环境预报中心提供的FNL全球分析数据或欧洲中期天气预报中心提供的再分析数据等其他全球场数据在本研究区域内更为准确,因此,本文使用经过同化的RMAPS-ST 3 km×3 km分辨率分析场。
为对比Jiménez方案效果,设计了3组模拟试验。其中T0为参照试验组,T1和T1C为对照试验组,其中T0未采用任何次网格地形方案,T1选用原始Jiménez方案,T1C采用经本文修正的Jiménez方案。每个试验组均设有水平分辨率3 km×3 km,1 km×1 km,333 m×333 m 3个单层模拟试验,并分别以1,2,3序号表示试验名称(表1)。试验组区别在于是否开启Jiménez方案,其他物理方案相同,边界层方案为YSU;微物理方案为New Thompson;长波和短波辐射方案均采用RRTMG,近地层方案为新MM5;陆面过程方案为Noah;积云方案不开启。静态数据中,地形高程数据采用SRTM1 1 s(分辨率约30 m)。

表1 模拟试验设计Table 1 Schemes of different experiments
1.3 模拟时间段选取
用于3组试验检验、分析的模拟时间段并未选择连续模拟(不小于30 d),而是挑选了2017年冬季和春季出现的3个大风天气个例。选择大风个例进行分析检验原因如下:①个例模拟可以选择中性条件、晴天少云天气,尽可能避免边界层、积云、辐射方案误差造成的影响,部分程度上削弱热力效应,使未使用次网格地形参数化方案的T0组中WRF近地面风速模拟结果更准确。再通过与实测风速进行对比,凸显复杂地形区域次网格地形对风场的影响,这样在对修正方案进行检验时更有针对性。②由于大风天气时风速较大,地形的动力因素占主导地位,使地形对近地面风速影响作用凸显。此时,WRF系统性偏差也达到最大,进而Jiménez方案对风速修正效果更显著[26],在此基础上,本文对Jiménez方案再修正的效果也显著且有追踪性。而连续模拟将包含小风或静稳天气,使地形对风速的影响不显著,修正效果也不显著。在计算检验统计量时会出现平均小风和静稳天气结果,反而会掩盖WRF模式系统性偏差及Jiménez方案缺陷。另外,本文为消除个例巧合性,在易出现晴天大风天气的冬春季节挑选了3个个例,分别为2017年1月13—14日、2月8—9日和3月5—6日。其中在3个个例中西大庄科站、二海陀站、小海陀站平均风速分别为3.5 m·s-1,9.4 m·s-1,6.0 m·s-1;最大风速分别为13.7 m·s-1,26.2 m·s-1,24.9 m·s-1。每个个例连续模拟48 h,并提前12 h 作为模式调整时间,输出间隔为10 min。
2 次网格地形方案修正方法
2.1 Jiménez方案简介
由于WRF在模拟中对地形采取平滑处理,但并未考虑次网格地形阻力,致使近地面风速模拟结果在平原、山谷及风速较小处偏大,在高山和丘陵风速偏小。Jiménez方案[25-26]通过在动量守恒方程的动量下沉项中引入参数Ct订正地形调节与植被有关的地表拖曳力Fveg,以减小平原和山谷的风速,并尽可能增加山顶风速:
(1)
式(1)中,u和v分别代表模式第1层的水平风分量风速,u*表示摩擦速度,Δz是模式第1层垂直网格厚度。Ct是与地形特征有关的地形高度h的算子Δ2h(也写作LapH)和次网格尺度地形高度标准差σSSO的函数。当Δ2h≥-20时,Jiménez方案认为是山谷时将逐步过渡减小风速:
Ct=
(2)
α=(Δ2h+20)/10。
(3)
Ct=
(4)
式(4)中,当Δ2h<-20时,认为该地区为山地或者丘陵,通过逐渐减小Ct建立与高空风速的关系补偿低估;当Δ2h≤-30时,则完全不考虑地表拖曳作用。在模拟中Δ2h由读取的地形高度数据集通过式(5)在WPS预处理中计算获得,σSSO为WPS直接读取σSSO数据集获得。在未开启地形订正方案或区域为平坦地形时,Ct=1,不进行任何修正。Jiménez方案目前仅耦合在YSU边界层方案[25]中,可通过设置选项开启。具体参数化方案完整公式可参见文献[25-26]。
Δ2hi,j=0.25(hi+1,j+hi,j+1+
hi-1,j+hi,j-1+4hi,j)。
(5)
2.2 Jiménez方案存在的问题
实际模拟中发现Jiménez方案在不同模式水平分辨率下,原本Jiménez方案应起到减小山谷风速、增加山顶风速的效果,却时常出现相反结果,图3为T1与T0试验组10 m模拟风速差值场,其差值场为3个个例的集合平均。
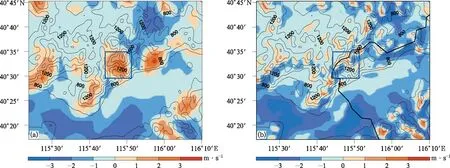
图3 3个个例10 m风速差值集合平均场(填色)(等值线表示地形高度,单位:m)(a)T1_1与T0_1的差值,(b)T1_2与T0_2的差值,(c)T1_3与T0_3的差值Fig.3 Ensenble averaged bias of 10 m wind speed of 3 cases(the shaded)(the contour denotes the terrain height,unit:m)(a)difference between T1_1 and T0_1,(b)difference between T1_2 and T0_2,(c)difference between T1_3 and T0_3

续图3
3 km×3 km分辨率时,T1与T0试验10 m风速差值在等高线密集的山区大多为正值,Jiménez方案对10 m风速有明显增大作用。其中小海坨山范围全区风速增大最为显著,幅度高达3 m·s-1。相反,在等高线稀疏的平原和山体背风坡风速较小处的山谷,Jiménez方案对风速有减小作用。仅从设计效果初衷看,Jiménez方案有效(但在单站对比中仍存在较大问题,见图4)。1 km×1 km分辨率下,Jiménez方案同样也达到减小山谷风速、提高山顶风速效果,但修正幅度明显小于3 km分辨率。其中在小海坨山范围,风速差值场不仅出现正值区也出现负值区,且正负区域与实际地形对应较好,正值区对应小海陀山呈“M”型的山脉顶部,负值区为较平缓的山谷底部,说明1 km时高分辨率模拟在对地形描述上优势很大。同时随着水平分辨率提高,Jiménez方案对次网格地形处理也随之精细化,仅通过Δ2h水平分布就能很好地分辨出山体局部特征。而当分辨率进一步提高至333 m×333 m,风速差值场在模拟区域全区内基本为负,Jiménez方案不仅对山谷地区风速起到减小作用,也减小了山顶风速,Jiménez方案修正结果出现明显错误。

图4 3个个例西大庄科站、二海陀站、小海陀站T0和T1试验10 m风速模拟与实测偏差的平均日变化Fig.4 Ensemble averaged daily bias of simulated and observed 10 m wind speed at Xidazhuangke,Erhaituo and Xiaohaituo of T0 and T1 from 3 cases
为进一步与实测比较,图4给出西大庄科、二海陀、小海陀站点T1及T0模拟与实测10 m风速偏差的平均日变化。由于水平分辨率不同,模式在对静态数据、大气物理过程等计算精度上也不同,所以低分辨率模拟风速插值到单站不如高分辨率,或更高分辨率模拟结果由于受其他物理方案在“灰区尺度”[31]因不可分辨因素影响造成不及低分辨率,这均可以理解且暂不可避免。但本文关注重点并非不同分辨率对风速模拟准确性,而是不同分辨率下Jiménez方案对近地面风速修正的有效性及原因。
图4中,T0与实测风速偏差显示出WRF系统性偏差问题,表现为代表山谷的西大庄科站风速偏大,山顶站二海陀站、小海陀站风速偏小。14:00—22:00(北京时,下同),实际风速(图中未给出)较大时WRF的系统性误差较大,而此时Jiménez方案修正效果最明显,这也是本文挑选大风个例的原因。随着模式分辨率增加,系统性误差略减小,但仍存在(表2)。

表2 10 m风速统计检验结果(单位:m·s-1)Table 2 Statistic results of simulated 10 m wind speed(unit:m·s-1)
山谷西大庄科站,除T1_1外,Jiménez方案能按预期对风速有减小的修正效果。而在T1_1在西大庄科站对近地面风速却有明显增补,增幅平均达1.8 m·s-1,但偏差较T0_1反而更大。1 km分辨率下,Jiménez方案分别减小山谷并提高山腰、山顶风速,能有效缩小与实测的偏差。而333 m分辨率下,同其他个例结论相似,同样存在Jiménez方案修正错误的现象,尤其对山顶站,使用Jiménez方案反而使原本低估的风速进一步减小。
为寻找Jiménez方案在3 km和333 m分辨率下失效原因,需从方案中引入的调整项Ct着手。从式(2)~式(4)可知Ct主要与Δ2h和σSSO有关。对σSSO来说,只有在非常平坦的地区才可能小于e,且σSSO只参与对山谷地区做减小风速的修正,并不影响山顶区域。在模拟区域333 m分辨率下,其读取的σSSO基本大于e,σSSO对Ct的计算影响不大,失效主要问题来自Δ2h变量,其分布如图5所示。
图5分别给出3 km,1 km,333 m 3种水平分辨率下在整个模拟区域和小海坨山区域Δ2h水平分布。低分辨率时,Δ2h绝对值较大,随着分辨率提高,Δ2h绝对值逐渐向0靠近。就小海坨山局地区域而言,3 km分辨率的Δ2h值分布几乎无法分辨出山谷、山顶等局地山体形态。Jiménez方案中用于区分山体形态判断阈值-20,对于3 km下的小范围内几乎不起任何参考性。如代表山谷的西大庄科站所在网格内由于地形复杂程度大,平滑过滤的次网格地形海拔高度差大,其Δ2h<-20而被Jiménez方案判定为山顶而进行了增幅修正。由此可知,-20不适合作为3 km分辨率山体形态特征判断依据。但由于3 km网格分辨率低,也无法找到其他合适阈值,这也进一步说明复杂地形区域开展风场高分辨率模拟的必要性。1 km分辨率时,阈值-20能较好地分辨局地山体的形态特征。当分辨率继续增加到333 m时,发现小海陀山范围内Δ2h值已均大于-20,此时Jiménez方案将整个区域判断为平原而减小其风速(图4),这也是图4和图3中风速偏小的原因。所以333 m分辨率以下阈值取为-20显然不适用。若将Δ2h以0为界限却能分辨山脊和山谷形态,说明333 m分辨率以下存在可作为山体形态判据的Δ2h值。需要人为重新依据区域地形特点在不同分辨率下设定合适的判据,尤其是高分辨率下的阈值,修正弥补Jiménez方案缺陷。

图5 模拟区域和小海坨山区域不同水平分辨率Δ2h水平分布(填色)(等值线表示地形高度,单位:m)Fig.5 Δ2h distribution of computational domain and Xiaohaituo Mountain with different resolutions(the shaded)(the contour denotes the terrain height,unit:m)
2.3 Jiménez方案的修正方法
为确定不同分辨率用于判断山体形态的阈值,首先需找出Δ2h与模式水平分辨率之间的相关关系。本文分别在小海坨山的山顶、山腰和山谷处各挑选10个点(如图6所示)。依次获取各点从3 km至100 m(分别为3,2.7,2.4,2.1,1.8,1.6,1.4,1.2,1.0,0.9,0.8,0.7,0.6,0.5,0.4,0.3,0.2,0.1 km)18个不同水平分辨率下对应的Δ2h值。

图6 小海坨山区域30个点的分布(填色表示地形)Fig.6 The distribution of 30 points in Xiaohaituo Mountain(the shaded denotes terrain)
Δ2h散点图(图7)显示当水平分辨率大于2 km时,所选点无论位置如何Δ2h均小于-20,即所有点均判为位于山顶;而当分辨率小于500 m时,大部分山腰点Δ2h已大于-20,即将山腰以上点已误判为山谷。分辨率过高或过低都将导致-20的判据做出错误判断。为修正山体形态的阈值,将30个点Δ2h值与水平分辨率进行线性回归,获得修正后的Δ2hc:
Δ2hc=-0.033dx+9.154。
(6)
式(6)中,dx为水平分辨率,单位为m。

图7 30个点不同水平分辨率下对应的Δ2h及拟合曲线Fig.7 The corresponding Δ2h values of 30 points at different resolutions
将原始Jiménez方案阈值-20带入新修正的式(6),其对应的最佳网格水平分辨率应为883 m×883 m,接近1 km,所以上文中原始Jiménez方案在1 km分辨率较3 km和333 m效果更佳。而原始Jiménez方案制定之初适用的2 km分辨率在小海坨山区域也不适用,2 km对应的阈值应该为-56,小于-20。按照上述关系进一步修正式(2)~式(4),得到式(7)~式(9)为检验修正后Jiménez方案的模拟效果,将修正式(6)~式(9)代入WRF的Jiménez方案中,分别对3个个例进行重新模拟。
(7)
(8)
(9)
3 结果检验
图8给出小海坨山区域3个个例T1C与T1试验风速差值平均场。T1C_1,T1_1减小了小海坨山全区的风速,尤其在山顶。原始Jiménez方案虽在1 km 分辨率下,效果最佳但仍略偏大,而T1C_2较T1_2平均略降低0~1 m·s-1。333 m分辨率下,修正后Jiménez方案使风速明显在“M”型山顶增加,在山谷等小风速地带略减小,弥补了由原Jiménez方案因阈值-20过小而造成全区风速错误减小的效果。


图8 3个个例小海坨山区域10 m风速差值集合平均场(填色)(等值线表示地形高度,单位:m)(a)T1C_1与T1_1差值,(b)T1C_2与T1_2差值,(c)T1C_3与T1_3差值Fig.8 Ensenble averaged bias of 10 m wind speed of 3 cases in Xiaohaituo Mountain(the shaded)(the contour denotes the terrain height,unit:m)(a)difference between T1C_1 and T1_1,(b)difference between T1C_2 and T1_2,(c)difference between T1C_3 and T1_3
为比对实测风速,图9分别给出3站点模拟与观测的偏差平均日变化情况,并在表2中分别给出T0,T1与T1C 3组试验组所选3个自动气象站10 m风速的平均偏差和均方根误差。T0试验组中,随着分辨率提高,平均偏差数值在减小,但333 m 分辨率下均方根误差值略大,这是由于高分辨率增加了风速脉动的模拟,使其风速分布更离散。T1试验组中,1 km分辨率统计检验结果明显好于3 km和333 m,而3 km和333 m反而差于T0,这也与上文结果一致,表明原始Jiménez方案失效。在T1C试验组中,在山谷站修正后的Jiménez方案较修正前降低了3 km分辨率风速,且在不同实际风速下修正效果不同,大风速时效果较差,但整体平均偏差和均方根误差绝对值数值上较T1更好。在山谷站,修正后的Jiménez方案分别提高了1 km和333 m风速,效果很好。在山顶站,尤其333 m分辨率下,较原始Jiménez方案,修正后Jiménez方案大幅度增加风速,弥补原始Jiménez方案把山顶当作山谷错误的减小风速的修正效果。T1C较T1在山顶站平均偏差和均方根误差绝对值数值上也分别减小,使模拟更接近观测。总之,修正后的Jiménez方案能很好地弥补原始Jiménez方案存在的缺陷,使其能适应不同网格分辨率模拟。

图9 3个个例西大庄科站、二海陀站、小海陀站T1C和T1试验10 m风速模拟与实测偏差的平均日变化Fig.9 Ensemble averaged daily bias of simulated and observed 10 m wind speed at Xidazhuangke,Erhaituo and Xiaohaituo of T1C and T1 from 3 cases

续图9
4 结论与讨论
本文基于高精度地形高程数据对Jiménez方案进行修正,分析了不同水平分辨率下Δ2h变化,找出合适的山体形态判断阈值,使其能适应不同分辨率,尤其是高分辨率模拟。在京津冀西部太行山复杂地形区域开展大风个例模拟,并利用3个自动气象站实测风速对比分析Jiménez方案修正前后对近地面风速模拟效果,得到以下结论:
1) WRF在复杂地形区域对近地面风速的模拟存在系统性误差,表现为平原、山谷等小风速地带偏高,山腰、山顶等大风速地带偏低的现象,且实际风速越大系统性误差越大。误差会随着模式分辨率的增加而减小,在复杂地形开展风场高分辨率模拟非常必要。
2) 原始Jiménez方案在不同网格分辨率下呈现错误的修正效果:在较低分辨率下,高估的平原、山谷地区风速被进一步增补;在高分辨率下,低估的山腰、山顶风速被进一步降低。因此,在复杂地形区域,尤其是高分辨率下是否开启次网格地形方案需慎重选择,必要时需提前评估。
3) Jiménez方案失效的主要原因来自方程中判断山体形态特征的Δ2h值并不适用于不同网格分辨率所致。通过高精度地形数据,本文建立小海坨山区域不同分辨率下Δ2h与网格分辨率的拟合关系,并修正原始Jiménez方案。发现修正后Jiménez方案在不同分辨率下能有效弥补原始方案缺陷,其低层风速平均偏差和均方根误差统计值均较原始Jiménez方案更优,能起到减小WRF系统性误差、使近地面风速更接近实测的效果。
本文主要目的是指出原始Jiménez方案在阈值拟定上存在的错误,不适于全尺度模式分辨率的模拟试验。由于原方案方程组中的Δ2h随模式网格分辨率增高而趋于零,本文再修正方法的要点是找出Δ2h趋于零的速率,虽然一元回归方法较为简单,但通过线性速率修正Δ2h后对模拟结果改进明显,也进一步说明Δ2h这一参数对模式分辨率有极大的敏感性,读者在开启该方案时需谨慎处理。另外,本方法在其他复杂地形区域理论上也能有利改善,尤其是进行高分辨率模拟时可供参考。但值得注意的是,由于本文修正主要源自小海坨山区域的地形高程数据,其他复杂地形区域其Δ2h随模式分辨率变化速率(斜率)是否一致,还需要在各地进一步开展模拟研究。但可以参考本文方法,制定适合所关注区域的修正方案关系。Jiménez方案在设计时用到的次网格地形参数仍较为主观,下一步可考虑引入代表地形起伏程度的参数,如地形分形特征,地形高度的功率谱特征等更客观且具有物理意义的参数,发展出更普适的次网格地形修正方案。

