融合标签的实值条件受限波尔兹曼机推荐算法*

张光荣，王宝亮，侯永宏

1.天津大学 电气自动化与信息工程学院，天津 300072

2.天津大学 信息与网络中心，天津 300072

1 引言

随着信息时代的到来，信息过载[1]使得用户很难从海量的数据中找到自己感兴趣的内容，针对用户兴趣的推荐算法（recommendation algorithm）应运而生。推荐是根据用户的个人历史行为信息，预测出用户的个性化偏好，从而为用户提供可能感兴趣的商品，目前已成为电子商务、视频音乐点播、新闻推送等领域的核心技术[2]。

推荐算法也面临着一系列的问题，数据稀疏性（sparseness）就是其中之一。数据稀疏性是指用户历史行为数据总量巨大，但具体到每一个用户，能利用的数据却十分稀少[3]。推荐系统（recommended system）自定义至今，针对数据稀疏性难题，研究人员提出了各种方法予以缓解，主要有两种思路：第一是基于数据填充方法，主要思想是借助其他信息建立有效的用户模型，以此缓解用户历史数据的稀疏性；第二是不借助其他数据建立模型，直接利用用户历史评分信息，通过矩阵分解（matrix factorization）、聚类（cluster）、机器学习（mac-hine learning）等对用户历史评分数据进行预处理[4]。

本文通过融合以上两种思路，把表达用户对商品属性认知的标签，通过算法预处理，加入至机器学习模型，提出融合标签的实值条件受限玻尔兹曼机推荐算法——Tag_R_CRBMs，降低推荐算法中数据的稀疏性。

本文第2章介绍相关工作；第3章主要介绍本文提出的融合用户标签的实值条件受限玻尔兹曼机推荐算法；第4章内容为基于MovieLens数据集的实验结果及分析；第5章对全文进行总结。

2 相关工作

在借助其他信息缓解数据稀疏中，文献[5]提出一种基于项目相似度的数据填充方法，其目的在于当原始数据集极度稀疏时通过数据填充为算法提供足够的数据支持。文献[6]通过用户隐含的反馈，例如在页面停留的时间、听一首歌的时长、选择商品的顺序，隐含反馈信息与用户已有的历史信息结合，组成一个混合的推荐系统。

随着Web2.0的到来，标签（tag）成为一种有用且能很好反映用户偏好的文本信息[7]，在对标签的处理中，主要有潜在Dirichlet分布（latent Dirichlet allocation，LDA）模型、TF-IDF（term frequency-inverse document frequency）模型、Word2vec模型。文献[8]在标签系统中运用LDA模型，以此来发现用户与标签、资源与标签之间的潜在语义关系，并计算用户选择某个资源的条件概率，然后将计算出的概率与通过协同过滤算法计算出的资源相似度相结合，预测用户偏好值。TF-IDF是一种统计方法，用以评估一个词对于一个文档集或者一个语料库中的某一份文档的重要程度，字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比例下降[9]。Word2vec是Google推出的词嵌入（word embedding）的开源工具，为一群用来产生词向量的相关模型，这些模型为双层的神经网络（neural network，NN），用来训练以重新建构语言学的词文本[10]。以上三种模型，TF-IDF以其容易理解，计算简单的优点，在计算用户对标签偏爱度上脱颖而出。

在借助学习模型对数据进行预处理方法中，矩阵分解方法首当其冲，主要有奇异值分解（singular value decomposition，SVD）[11]、隐因子模型（latent factor models，LFM）[12]、非负矩阵分解（non-negative matrix factorization，NMF）[13]、基于概率的矩阵分解（probabilistic matrix factorization，PMF）[14]。矩阵分解模型通过减少用户-商品评分矩阵的维数，能在一定程度上缓解用户历史数据稀疏性。矩阵分解中因子的选取至关重要，因子越能准确地描述用户偏好与商品特征，推荐结果越准确。现有矩阵分解推荐算法通常采用商品类别构成因子向量，然而商品类别并不足以精准描述用户偏好和商品特征，限制了矩阵分解推荐算法性能进一步提高。

随着近年来深度学习（deep learning，DL）的兴起，基于深度学习的推荐模型快速发展[15]，其中以受限玻尔兹曼机（restricted Boltzmann machine，RBM）模型以及条件受限玻尔兹曼机（conditional restricted Boltzmann machine，CRBM）模型最受欢迎[16]。2013年Georgiev等[17]提出显层为实值的单元的受限玻尔兹曼机（real-valued restricted Boltzmann machine，R_RBM）模型，使得模型训练得到简化，性能获得提升。文献[18]在实值条件玻尔兹曼机里引入了好友之间的信任关系，缓解了数据稀疏性，提升了推荐的准确性。

虽然研究者对两个思路都进行了深入的研究，但两个思路结合，尤其是把标签与深度学习模型结合的研究相对欠缺。基于此，本文提出了Tag_R_CRBMs算法。首先，引入文本分类当中的TF-IDF算法，得出用户对其所使用标签的喜爱程度，与标签基因（taggenome）[19]数据相乘，可以得到用户对具有使用过标签属性的商品的评分，标准化预测商品评分使其在0～5的范围内。其次借鉴文献[17]和文献[18]思想，提出显层单元为实值的条件受限玻尔兹曼机（realvalued conditional restricted Boltzmann machine，R_CRBM）模型，此模型不需要把实值评分转化为整数值评分，减少了显层的参数，R_CRBM模型显层输入为通过标签的预测评分与用户历史评分，条件层输入用户潜在的评分/未评分{0,1}向量与使用标签/未标签{0,1}向量。最后训练模型，获得模型的参数。Tag_R_CRBMs算法流程图如图1所示。

本文的Tag_R_CRBMs算法的主要贡献有两方面：第一，应用TF-IDF算法与标签基因数据把用户标签数据转换为用户评分数据，缓解了用户评分数据的稀疏性；第二，在R_CRBM模型的条件层中，加入了用户潜在的使用标签/未使用标签信息。

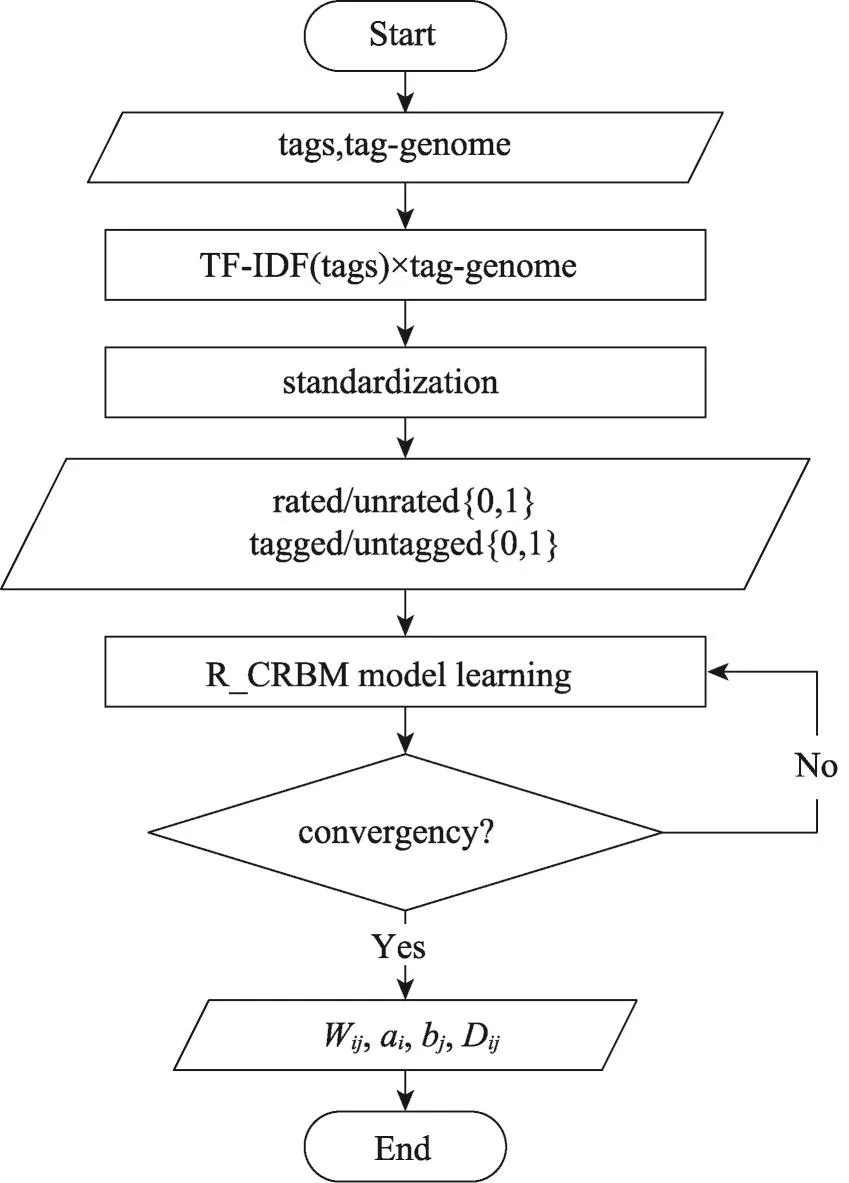
Fig.1 Workflow of Tag_R_CRBMs algorithm图1 Tag_R_CRBMs算法流程图

3 Tag_R_CRBMs算法描述

3.1 用户对标签的喜爱度

用户对商品所应用的标签是用户对商品态度一个很好的反馈，用户可能对同一个商品使用多个标签，也可能对多个商品使用同一个标签，本文引入TF-IDF算法获得用户对标签的喜爱度。

TF-IDF是一种用于信息检索与数据挖掘的常用加权技术，TF（term frequency）为词频，表示一个词在文档中出现的频率，IDF（inverse document frequency）为逆文档频率，是一个词普遍重要性的度量。令U={u1,u2,…,un}为用户集合，T={t1,t2,…,tk}表示用户所使用的标签集合，用户对所应用标签的使用频率为：

式（1）中，分子表示用户u对标签t的使用次数，分母表示用户使用标签的总次数。

用户u对标签t的逆文件频率为：

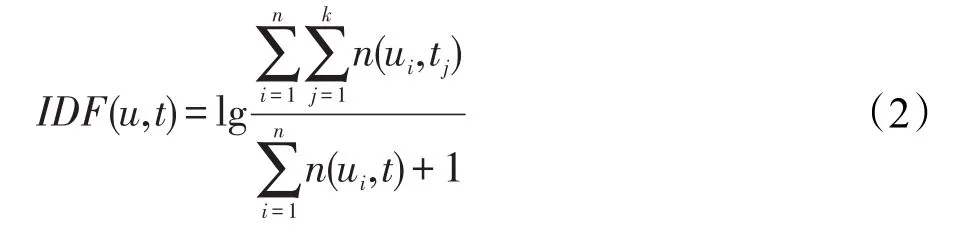
其中，n(ui,tj)表示标签tj被用户ui使用的次数，n(ui,t)表示用户ui对标签t使用的次数。IDF(u,t)是标签t对用户u普遍重要性的度量，表明标签t被不同用户使用的可能性。

用户对其标签的喜爱程度即用户对其使用标签的TF-IDF为：

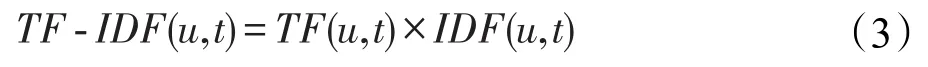
对于标签集合中，用户没有使用过的标签，其TF-IDF值设为None。用户对标签的TF-IDF矩阵如表1所示。

Table 1 User-tag TF-IDF matrix表1 用户-标签TF-IDF矩阵

3.2 基于标签的用户商品评分预测

3.1节获得了用户对标签的喜爱度，本节通过利用标签基因数据与用户对标签的喜爱程度相乘，得到用户-商品预测评分。

标签基因是一种提升传统标签模型的数据结构，目的是更好地提供与用户的交互。I={i1,i2,…,im}是商品集合，用rel(t,i)∈[0,1]量化每个标签t∈T与每个商品i∈I之间的关联度，rel(t,i)为0表示不相关，为1表示强相关。定义标签基因G为标签-项目矩阵，数学公式为：

其图像化描述如表2。

基于隐因子分解模型的思想，用户对标签t∈T的偏爱度很高，商品i∈I和标签t∈T强相关，那么可以预测用户对商品i∈I拥有较高的喜爱度，因此预测用户对商品的评分值如下式：

Table 2 Relevance table between tags and items表2 商品与标签之间的相关性表

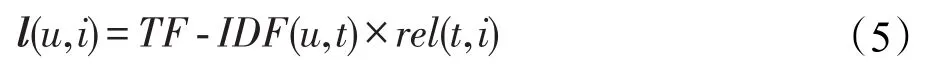
其中，l(u,i)表示预测的评分，由于用户对标签应用的缺失，l(u,i)也是一个充满缺失值的预测评分矩阵。由于用户历史评分数据范围为[0,5]，l(u,i)需要进行规范化到0～5范围内。

如式（6）所示，rp(u,i)为规范化后的评分，min(l(u,i))为l(u,i)的最小值，max(l(u,i))为l(u,i)的最大值。

3.3 实值条件受限玻尔兹曼机模型R_CRBM

RBM是Smolensky基于波尔兹曼机（Boltzmann machine，BM）提出的一种根植于统计力学的随机神经网络，Salakhutdinov首先运用RBM于推荐领域，并同时提出了CRBM模型[16]。本文依据已有研究，提出显层单元为实值的条件受限波尔兹曼机（R_CRBM）模型，模型如图2所示。

Fig.2 R_CRBM model图2 实值条件受限玻尔兹曼机模型

设有m个商品，n个用户，用户对商品的反馈为0～5的实值评分，V={v1,v2,…,vm}为显层单元，其输入为实值评分数据，H={h1,h2,…,hF}为隐藏单元，F表示隐藏单元的数目，H为0,1二值单元，r表示条件向量，W表示隐层与显层的连接权重，r∈{0,1}m，用以表示用户的特征信息，本文表示用户其潜在评分/未评分、标签/未标签信息，D表示r对H的影响矩阵。

依据R_CRBM模型的层内无连接，层间全连接的特点，当给定可见单元与条件单元的状态时，第j个隐单元的激活概率为：

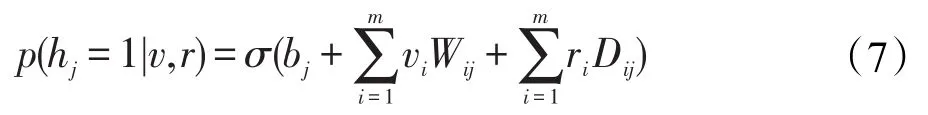
式（7）中，σ(x)=1/[1+exp(-x)]为sigmoid的函数，bj为隐层单元的偏置。

当给定隐单元的状态时，显层第i个可见单元的值为：

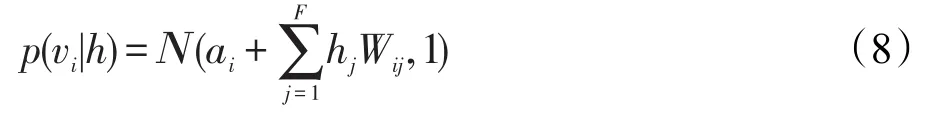
式（8）中，Ν为高斯分布，ai表示显层单元的偏置。

3.4 R_CRBM模型的训练

训练R_CRBM模型的目的是求出各参数的值，包括显层偏置ai、隐层偏置bj、显层与隐层的连接权重Wij，以及条件层与隐层的单向连接矩阵D，参数的获取可以利用最大化R_CRBM在训练集上的对数似然函数学习得到[20]。把显层单元设置为一组训练样本，利用式（7）计算所有隐单元的二值状态，在所有隐层单元的状态确定后，根据式（8）来确定第i个可见单元vi的取值进而产生可见层的一个重构（reconstruction）。使用随机梯度下降法（stochastic gradient descent）最大化对数似然函数在训练数据上的值时，各参数的更新准则为：

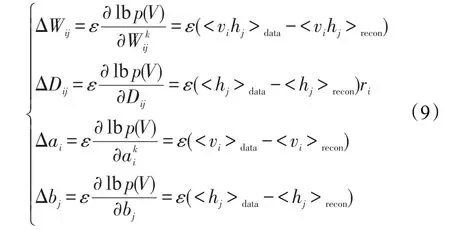
其中，ε为学习率（learning rate），＜⋅＞data表示训练数据分布，＜⋅＞recon表示T步采样计算后的数据的分布。整个训练如算法1所示。

算法1R_CRBM模型基于CD的训练算法

输入：评分矩阵ratings，条件向量ri，隐单元个数F，学习率ε。

1.Initialize：visible units,conditional layer,Wij,Dij,ai,bj

2.while model is not convergence

3.fort=1,2,…,T

4.fori=1,2,…,F

5.utilize formula(7)to gethi

6.end for

7.forj=1,2,…,m

8.utilize formula(7)to getvj

9.end for

10.utilize formula(10)to update parameters

输出：显层隐层连接矩阵Wij，条件向量与隐层连接矩阵Dij，显层偏置ai，隐层偏置bj。

模型训练完成后，对于某个具体用户，输入用户历史评分数据和经过计算获得的基于标签的评分数据以及条件向量数据至训练好的R_CRBM模型，得到的显层单元的值为用户对商品的预测评分。

4 实验结果分析

本章通过实验验证本文所提算法性能，实验数据集采用的是 MovieLens(http：//movielens.org)中的ml-20m数据集，采用5-折交叉验证法(5-fold cross validation)进行模型训练，以文献[17]和文献[18]的算法作为对比结果。文献[17]改进了CD算法，其改进方法为可见单元的值等于对应隐单元连接权重的和（sum weight）再加上偏置，称之为S_RBM模型。文献[18]在R_CRBM模型中加入了基于MoleTrust[21-22]最近信任好友关系（nearest trusted friends based on MoleTrust，NTFMT），称之为R_CRBM_NTFMT算法。

4.1 实验数据集介绍

本文选取MovieLens的ml-20m数据集应用标签数量大于10条的用户，数据量信息如表3。

4.2 评价指标

本文应用的度量方法有平均绝对误差(MAE)、均方根误差（RMSE）。

平均绝对误差计算预测值与用户实际评分值之间的平均绝对误差，能很好地反映预测值误差的实际情况，其计算公式如式（11）：

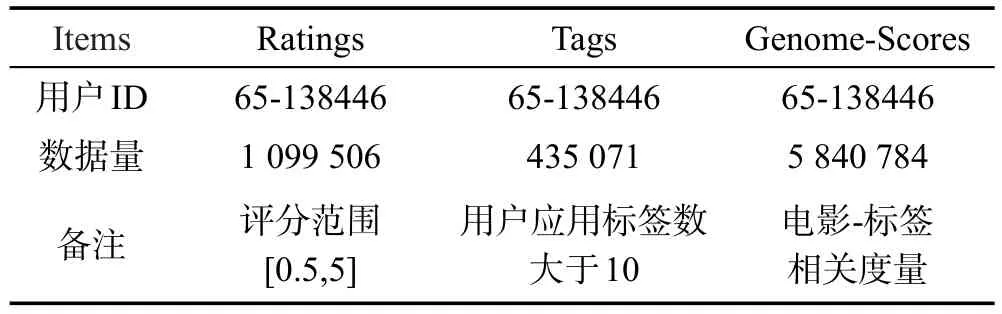
Table 3 Experimental dataset information表3 实验数据集信息

其中，Ntest表示测试数据集，ru,i表示实际用户评分数据集，restimated表示预测评分，|Ntest|表示测试数据集的个数。

RMSE用来衡量观测值与真值之间的偏差，是观测值与真值偏差的平方和与观测次数比值的平方根，其计算公式如式（12）：

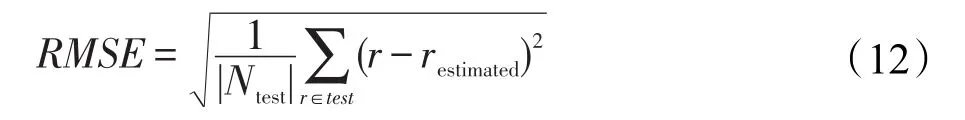
其中，Ntest表示测试集中用户数量，|Ntest|表示测试数据集的个数，r表示用户实际评分值，restimated表示R_CRBM模型的预测值。

4.3 实验结果分析

4.3.1 R_CRBM中隐藏单元的确定

本实验的目的是确定R_CRBM模型的隐单元数目，实验中显层单元的输入数据为用户商品评分矩阵，条件层输入数据为用户潜在的评分/未评分数据。实验是基于Epochs=20进行的，其实验结果如图3、图4所示。

如图3、图4所示，横坐标表示隐单元的数目，纵坐标分别表示RMSE、MAE的值。实验结果反映出，隐单元数目对RMSE和MAE的影响是先好后坏，符合实际情况。隐单元数量过少，不能完全表达出数据的特征，是欠拟合的状态；隐单元数量过多，容易出现过拟合。依据本实验结果；隐单元数量为90时，隐单元数量足够表达数据的特征，因此本文后续实验选择隐单元数量为90。

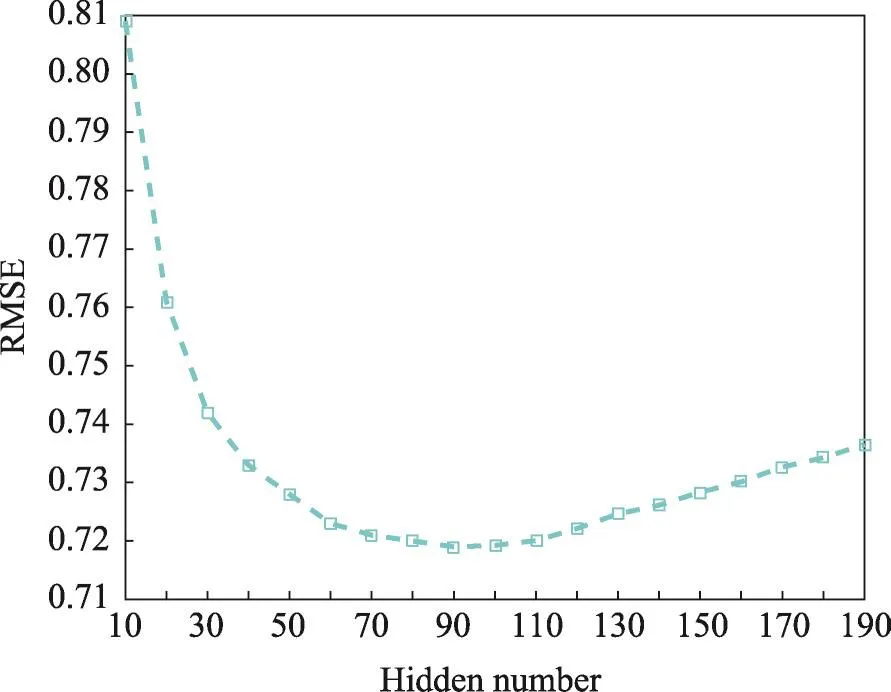
Fig.3 Influence of hidden number on RMSE图3 隐单元数目对RMSE的影响

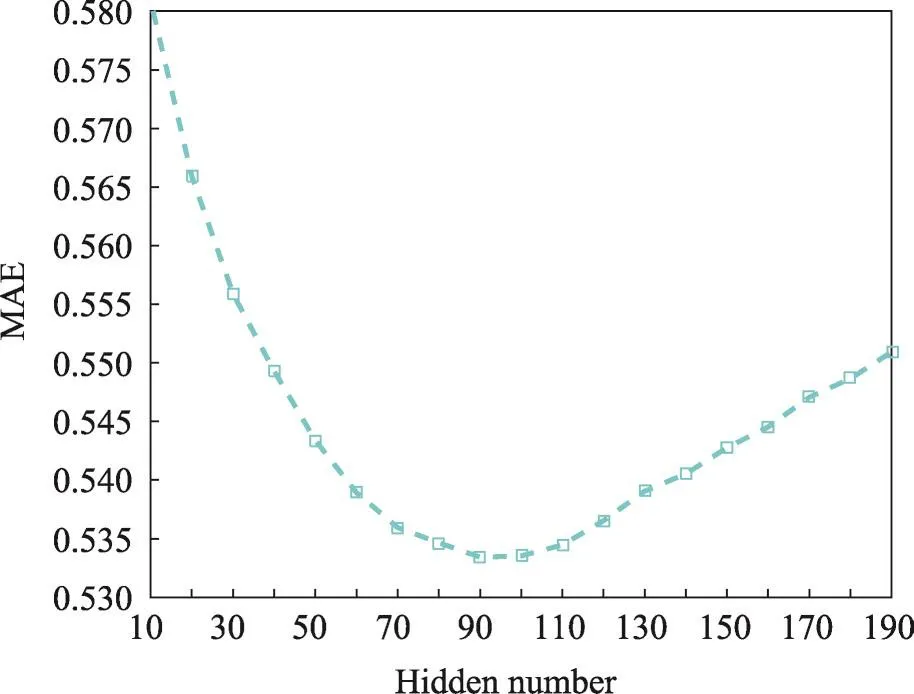
Fig.4 Influence of hidden number on MAE图4 隐单元数目对MAE的影响

4.3.2 条件层加入标签/未标签{0,1}向量影响

本文的一个贡献为在条件层数据中加入了用户潜在的标签/未标签数据，本节对向量加入的影响进行验证。

本文验证方法为使用两个R_CRBM模型，两个模型显层单元输入为用户商品评分数据，一个条件层的输入为用户潜在的评分/未评分数据，取名为R_CRBM模型；一个条件层输入数据为用户潜在评分/未评分、标签/未标签数据，取名为R_CRBM_C模型。隐单元数量为90，其RMSE、MAE对比结果如图5、图6所示。

从图5、图6可以看出，两个模型都在Epochs=10时开始收敛，在Epochs=70时模型收敛速度基本不变。条件向量中加入用户潜在的标签/未标签信息有助于模型的收敛，使模型的预测结果更加准确。同时也说明，用户与商品的交互信息越多，越能反映出用户对该商品的喜爱程度。

4.3.3 模型对比实验结果与分析

本节的模型对比实验中，一共包括5种模型，分别是本文的Tag_R_CRBMs模型以及4个对比模型，分别是最经典的RBM模型与CRBM模型[16]，文献[17]的S_RBM模型以及文献[18]的R_CRBM_NTFMT模型。各模型的RMSE以及MAE如图7、图8所示。

如图7、图8所示，5种模型的收敛速度大致相同，都是在Epoch为10时开始收敛，在Epoch达到70的时候，各模型的收敛速度基本不变。从图中RMSE与MAE的值可以看出，文献[17]的S_RBM模型以及文献[18]的R_CRBM_NTFMT模型明显优于经典的RBM与CRBM模型，而本文提出的Tag_R_CRBMs优化效果明显，取得了理想的预测结果，说明本文所提方法具有一定准确性与有效性。

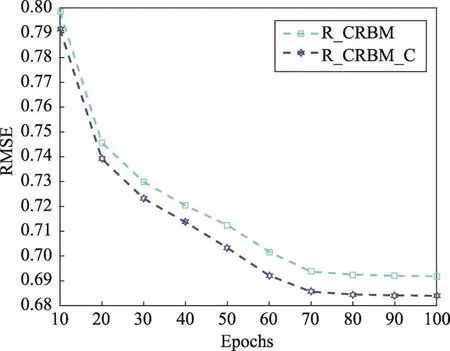
Fig.5 Influence of conditional layer input data on RMSE图5 条件层输入数据对RMSE的影响

Fig.6 Influence of conditional layer input data on MAE图6 条件层输入数据对MAE的影响

Fig.7 RMSE of five comparable models图7 5个对比模型的RMSE

Fig.8 MAE of five comparable models图8 5个对比模型的MAE

5 结束语

本文针对推荐算法中数据稀疏性难题，提出融合标签的实值条件受限玻尔兹曼机推荐方法。采用MovieLens数据集对本文提出的方法进行测试，并对结果进行了展示与分析，实验结果表明了本文提出的推荐方法的有效性。

用户的历史信息数据量巨大，更新速度快，如何在尽可能多的利用用户历史信息条件下，降低时间复杂度，实时快速准确地为用户提供感兴趣的商品，是今后研究的重点。