堤防渗流数值模拟与防渗方案研究
(南京市长江河道管理处,江苏 南京 210011)
1 研究背景
堤防渗流是指水体在堤防内部的流动,可引发管涌和背坡面滑动等不同形式的堤防破坏与变形,甚至可直接导致堤防决口,造成极大的危害与损失[1-4]。因此,堤防渗流的计算与防渗方案研究是堤防工程设计、堤防除险加固措施制定的关键环节,关系到人民的生命财产安全[5]。渗流及其破坏分析的主要对象包括浸润线、渗流量、坡降与渗流流速等变量[6-8]。目前,主要分析方法有经验法、流网法、物理模拟法和数值模拟法[9-10],各方法的定义及其优缺点如下。
(1)经验法。采用经验公式确定渗流影响与参数之间的关系,如可采用Sellmeijer经验公式确定作用于结构上的水头与管涌侵蚀长度之间的关系;采用IWHR法分析渗透破坏模式和土颗粒组成之间的相关关系等。该方法的分析过程最为简单,但精确度较低,且适用性差异较大。
(2)流网法。该方法是求解渗流动力学的拉普拉斯方程的图解方法,对服从达西定律的平面恒定渗流,通过绘制由流线和等势线组成的流网,求得渗流场内任意点的渗流要素。该方法操作较为简单,适用范围较广,可用于有压和无压渗流;精确度虽高于经验法,但依旧难以满足高质量的工程精度要求。
(3)物理模拟法。主要是通过建立缩小尺度的物理模型,并进行渗透试验来对原型的渗流过程与破坏进行研究。物理试验法一般被认为是渗流研究的最有效方法,精度最高,但需要消耗大量的人力、物力与时间,且可能存在比尺问题。
(4)数值模拟法。主要是基于水力学原理,采用计算机对控制方程进行求解,得到水流在堤防内的流动状态。该方法不仅可保证足够的精度,同时也保持较低的成本[11-12],综合了以上各方法的优点。随着数学模型和计算机资源与技术的进步,该方法正逐渐成为渗流分析的主要方法[13-14],但不同的数值模型可能存在一定的精度差异,因此有必要对其进行性能评价与比选。
堤防防渗对于维护堤防稳定性、防治渗流破坏或变形具有重要作用[15]。防渗方案一般可分为两种类型,一类是提高堤防材料本身的抗渗能力,一类是控制堤防内的渗流。前一类方法一般适用范围较窄,故后一类方法较为常用。控制渗流的方法又可以采取防渗法、排水减压法,其中防渗的方法是在堤防建筑物或地基中利用弱透水材料筑防渗体以截断渗流, 减少渗透流量, 防止地基与其堤防建筑物的渗透破坏, 确保渗透稳定性; 排水减压是一种疏导的方法, 将透水良好的的材料预先有计划地布置于堤防建筑物或地基中渗透比降较大的部位作为排水体, 使渗流提早释放渗透压力, 并通过排水体自由排出, 以确保地基与其堤防建筑物的整体安全[16]。方案的选择要根据具体的建筑物、工程、经济情况而定,考虑因素较为复杂,可采用数值模拟法对各项方案下的渗流性能进行模拟,为方案制定提供科学依据。
在此背景下,首先根据堤防渗流的物理试验,分别采用双重介质(Dual-porosity)、van Genuchten、修正van Genuchten、Kosugi、和Brooks-Corey共5项不同的数值模型对堤防渗流进行模拟,并将模拟结果与试验测量结果进行比对与分析,以评价各模型在堤防渗流模拟中的有效性。再采用已验证的数值模型模拟堤坡铺膜方案与堤坡铺膜结合坡脚防渗墙方案下的渗流特性,从而对两项方案的效果进行分析。目前,关于以上各模型在堤防渗流模拟中的适用性比较和基于数值模拟法的防渗方案效果分析均鲜有报道,因此相关方法与成果可为堤防渗流的数值模拟和防渗方案的制定提供经验与借鉴。
2 研究方法
2.1 控制方程
堤坝渗流可采用经典的里查德森公式:
(1)
式中,θ为堤防土质的体积含水率,%;t为时间,min;x和z分别为水平与垂直方向的坐标,cm;k(θ)为堤防土质的渗透系数,%;z为柱坐标系下的垂直向坐标,cm;K(θ)为非饱和土质的渗透系数, cm/min。饱和透水系数一般可根据测定的或者拟合的土壤水分特征曲线来推定,非饱和透水系数的确定具有较大的不确定性,可采用不同的模型,而不同的模型具有不同的性能,因此,有必要对不同的模型进行比较。研究的模型共包括双重介质、van Genuchten、修正 van Genuchten、Kosugi和Brooks-Corey共5项模型。
双重介质模型的表达式为
(2)
(3)
式中,i为区分编号;Ks为饱和导水率,cm/min;k为分区数;w为经验参数,无量纲。
vanGenuchten模型的基本公式为
(4)
(5)
(6)
式中,θ为体积含水率,%;h是压力水头,cm;θr和θs分别表示剩余和饱和体积含水率,%;Se为水饱和度,%;α、n、m、λ为经验参数,无量纲。
修正van Genuchten模型可表示为
(7)
(8)
式中,K0为拟合参数,无量纲;θm和F(Se)的公式分别为
θm=θr+(θs-θr)(1+|αhs|n)m
(9)
(10)
Kosugi模型可表示为
(11)
(12)
式中,erfc表示误差函数;h0为拟合参数,无量纲;σ为对数正态分布的标准差,无量纲。
Brooks-Corey模型可表示为
(13)
(14)
式中,hd为进气吸力,cm;hc为基质吸力,cm。
2.2 试验概况
试验数据主要基于河海大学朱伟与日本大学山村和也的堤防试验[17]。该试验的设置状况如图1所示,试验堤高7 m、宽34 m,在试验堤底部用黏土做了一个0.3 m厚的遮水垫层。试验开始时,将水位上升到设计高水位6.2 m(图1中右侧为迎水面),并一直保持高水位渗透,通过预先设置的水位测定仪对渗透浸润线进行测量,具体的试验参数可参见参考文献[11]。

图1 堤防渗流试验设置示意
2.3 模型设置
模型采用三角非结构化网格[18],如图2所示。该网格在不规则点处较密,而在其他位置相对较疏,因此可保持精确度与计算效率之间的平衡。计算时间步长为2 min。敏感性测试表明,更高的网格分辨率和更小的时间步长对结果的改变低于1%,满足精度要求。模型的初始条件可表示为
h(x,z,t)=h0(x,z)
(15)
式中,h0为初始的压力水头,cm。
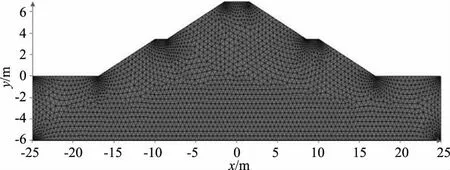
图2 堤防渗流数值模拟计算网格
数值模型的上边界不考虑蒸发和降水,表达式为
(16)
其他边界可视为无水量交换,因此设置为
(17)
(18)
2.4 防渗方案
物理试验是在江堤下部设置遮水垫层,而在相应的模拟中认为该垫层具有严格的不透水性,即底部土质的水分始终为0,有助于模型验证,但在实际工程中较难实现。因此在防渗方案的研究中,需要将不透水层改为砂土,再考虑不同防渗方案的效果。方案包括堤坡铺膜方案与堤坡铺膜结合坡脚防渗墙方案,见图3。在两种方案中,均在下游设置排水管,该排水管类似于实际工程中的排水棱体或减压井等。

图3 堤防防渗方案示意
3 研究结果
3.1 试验与模拟结果
实测和各模型模拟的浸润线时间变化情况如图4所示。根据实测和模拟结果可知,渗流过程大体可分为3个阶段。第一阶段,堤防内的浸润线逐渐抬高,但尚未达到最高点,形状呈凹型,持续时间大约为50 h,浸润线的渗透点在第三阶段达到最高点,但尚未达到堤防背水面。在此过程中,浸润线逐渐从50 h左右的凹型曲线向背面方向拓展,大约在200 h左右达到背面坡脚,之后浸润线缓慢上升,在约300 h后到达最高位,形成稳定渗流。如图4所示,各模型的模拟结果与试验结果基本一致,均可较为准确地模拟出渗流过程的3个阶段。

图4 堤防渗流试验与模拟结果
3.2 数值模型性能评价
为进一步评价各模型的性能,将堤防渗流试验与模拟结果进行对比,见图5。根据图5可知,双重介质模型明显高估了渗流的浸润线,Brooks-Corey模型则明显低估了堤防内的浸润线,因此不再考虑。Van Genuchten模型、修正van Genuchten模型和Kosugi模型的模拟值均与实测值较为接近,其中vanGenuchten模型在高点的估值偏高,在低点的估值则偏低;Kosugi模型与之相反,对浸润线高点的估值偏低,在低点的估值则偏高。相比较而言,修正van Genuchten模型在各时间点的浸润线预测结果均与实测值较为接近,因此该模型在模拟试验中性能最佳,可用于后续研究。

图5 堤防渗流试验与模拟结果对比
根据修正van Genuchten模型的基本公式可知,该模型仅能对各类型的土壤进行单独模拟,当各土层的边界较为明显时,该模型可以较为精确地模拟各个土层的非饱和透水系数。但在现实情况下,许多区域可能存在多种不同类型土壤混杂在一起的情况,此时该模型只能将混杂的土壤当做一个整体来进行模拟,其精度可能会受到较大影响,因此未来有必要对其进行改进以准确模拟混合土质的透水性。此外,该模型的参数也相对较多,需要大量测量数据来对其进行验证。而在实际工程设计中,往往缺少足够的测量数据,在一定程度上限制了其在实际工程中的应用,未来有必要开发具有同等精度但相对简单的模型。本文所采用的案例严格地控制了试验的边界条件且有较多的测量数据,有利于理论分析。分析表明,修正van Genuchten模型最为适用。
3.3 防渗方案效果分析
采用经过验证的数值模型对两种防渗方案进行模拟,其中方案1为堤坡铺膜方案、方案2为堤坡铺膜结合坡脚防渗墙方案,最终的渗流浸润线模拟结果见图6。根据模拟结果可知,堤坡铺膜不能够完全排除堤防内部的渗流,但可将浸润线从原始方案的6.2 m降低至1m左右,防渗效果明显。堤防中渗流的存在未必会导致堤防的渗透破坏,除渗透力外,还要综合分析堤防土质的抗渗强度[19],因此当堤防土质的抗渗强度达到要求时,该方案即可满足工程要求。

图6 堤防浸润线
当堤防土质的抗渗强度较弱时,则需要进一步采取措施,其中最典型的方案是在堤防坡脚处设置垂直防渗墙或截渗墙。根据模拟结果可知,该方案可进一步将浸润线降至底层,对堤防本身起到完全的防渗作用,效果明显优于原方案和堤坡铺膜方案,但在实际工程中,还应该根据具体情况进行选择,一方面防渗墙处的水头差较大,若地基土质较为松散,也可能造成地基破坏;另一方面防渗墙的修建需要消耗更多人力与物力。
4 结 论
(1)采用双重介质、van Genuchten、 修正van Genuchten、Kosugi、和Brooks-Corey 共5种不同的数值模型对堤防渗流进行模拟,得到不同时间点的渗流浸润线变化过程。将各模型的模拟结果与河海大学朱伟与日本大学山村和也的堤防试验测量结果进行比对与分析。结果表明:修正van Genuchten模型在堤防渗流的模拟中适用性最强。
(2)采用经过验证的修正van Genuchten模型模拟了堤坡铺膜方案与堤坡铺膜结合坡脚防渗墙方案两种情景下的渗流状况。结果表明:堤坡铺膜方案有明显防渗效果,而堤坡铺膜结合坡脚防渗墙方案则可完全将浸润线控制在堤防底层以下。相关模型与方法在南京市南师附中树人学校段江堤消险工程的渗流分析与除险加固设计中得到了实际应用,效果良好。但是,该方法仅能模拟渗流本身,而无法模拟堤防土体颗粒在渗流作用下的变形或移动,因此未来可进一步将渗流模拟与堤防变形的模拟进行耦合,以增强模拟方法的多功能性。

