静压有孔管桩的超孔隙水压力空间解析解
柳 俊 雷金波 张振礼 佘清雅
1.上海建工二建集团有限公司 上海 200080;2.南昌航空大学土木建筑学院 江西 南昌 330100
1 研究背景
静压管桩因其具有诸多优点而被广泛使用,但它是一种挤土桩,沉桩会引起桩周土体向上隆起和水平位移,同时会产生较高的超孔隙水压力,从而产生一系列的工程危害[1]。
文献[2]针对这种情况,对现有的管桩进行改造,提出了有孔管桩,能使土中孔隙水流入管腔,从而减小超孔隙水压力的最大值,并加速超孔隙水压力的消散。如何合理地确定沉桩引起的超孔隙水压力的大小、分布规律及消散过程,已成为学术界研究的重要课题。
国内关于超孔隙水压力已有许多研究成果,国外也有众多学者对其进行了深入研究。目前主要方法是通过理论公式进行估算和数值模拟计算。经典平面圆孔扩张理论解答只能反映初始超孔隙水压力沿径向的分布规律,不能反映其沿深度变化的规律。王旭东等[3]以Biot固结理论为基础,推导并获得了超孔隙水压力消散的三维解析解,但这些都是针对无孔管桩而言的。而对于静压有孔管桩产生的超孔隙水压力消散计算问题,还鲜有公开文献,仍值得深入研究。
本文基于圆孔扩张理论,从空间角度(径向距离r和深度z),对静压有孔管桩在软黏土地区沉桩过程产生的超孔隙水压力进行分析,得出有孔管桩超孔隙水压力的空间解析解。通过理论分析与数值模拟对比,为有孔管桩技术开发及工程应用研究提供了可靠的依据。
2 有孔管桩超孔隙水压力空间解析解
2.1 基本假定
1)土体均匀且不可压缩,服从Mohr-Coulomb准则。
2)土体中只包含孔隙水与土颗粒。
3)土体中的圆孔扩张的初始孔径为零。
4)土体的扩张速率与沉桩速率成一定比例关系。
2.2 超孔隙水压力的Henkel公式
目前计算超静孔隙水压力主要采用Vesic提出的Henkel公式,其表达式如式(1)、式(2)所示[4]:

式中:Δu——超孔隙水压力值;
β、αf——Henkel孔隙水压力参数,对于不同的土体参数是不一样的,对于饱和土,β=1;
Δσoct、Δτoct——八面体的正应力增量和剪应力增量;
Δσr、Δσθ、Δσz——径向应力增量、切向应力增量和竖向应力增量;
Af——Skempton孔隙水压力参数,可由式(3)得出。

式中:φ'——有效应力摩擦角;
q0——土的有效应力;
Cu——土的不排水抗剪强度。
2.3 超孔隙水压力空间解析解
大量实测资料表明,桩体贯入过程中,桩壁侧压力和桩侧摩阻力均随深度加大而增大,故应考虑深度z对超孔隙水压力的影响[5]。
本文的计算中,假设任意深度桩侧压力和摩擦力随深度线性增加,可以得到在任意深度z处桩侧压力Pz和摩擦力τz的表达式,如式(4)、式(5)所示[6]:
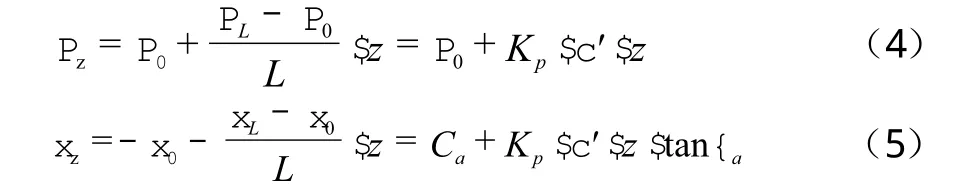
式中:P0——桩侧顶部侧向压力;
τ0——桩侧顶部摩擦力;
PL——桩侧端部侧向压力;
τL——桩侧端部摩擦力;
Ca——桩土界面黏聚力;
φ a——桩土界面摩擦角;
γ'——地下水位以下土的有效重度;
Kp——被动土压力系数;
L——桩长。
2.3.1 弹性区有孔管桩超孔隙水压力空间解析解
由弹性力学可知,无孔管桩在贯入中应分别满足下列3类方程[7]。
1)静力学方程:

2)几何方程(不考虑大变形):
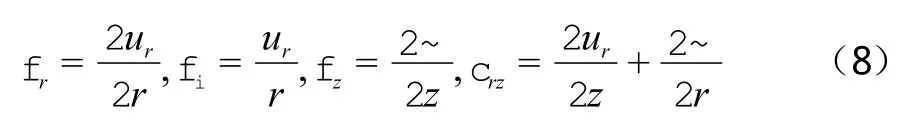
3)物理方程:
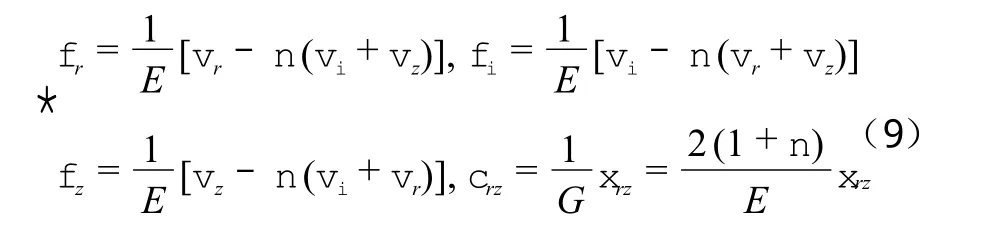
式中:σr、σθ、σz、τrz——土体的径向应力、切向应力、竖向应力和摩擦力;
εr、εθ、εz——土体的径向应变、切向应变和竖向应变;
ur——土体的径向位移;
ω——土体的竖向位移;
r——计算点到桩心轴线的距离;
μ——弹性区材料的泊松比;
E——材料的弹性模量;
G——材料的剪切模量。
为求得无孔管桩沉桩过程中满足上述3类方程的弹性区解答,先不考虑体积的影响,故平衡方程变为:
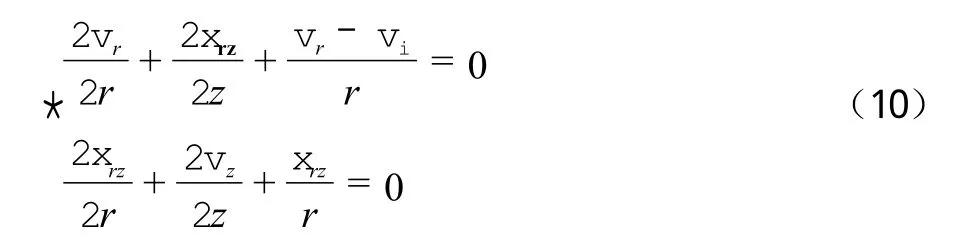
对于服从Morh-Coulomb材料屈服条件的饱和理想弹塑性材料,可将静压有孔管桩圆柱孔扩张问题近似看作平面应变空间轴对称问题,以求得扩张引起的总应力增量,然而塑性区小孔的排水排土过程会产生应力增量,2种情况相矛盾。
因此,土体实际总应力增量还应考虑小孔通道排水排土引起的应力增量,其中径向应力增量为∣Δσk∣,若假定土体总应力增量方向为正,∣Δσk∣为减少量,即∣Δσk∣>0。综合考虑∣Δσk∣的影响因素,根据试验分析建立 Δσk与Δσr之间的关系式:
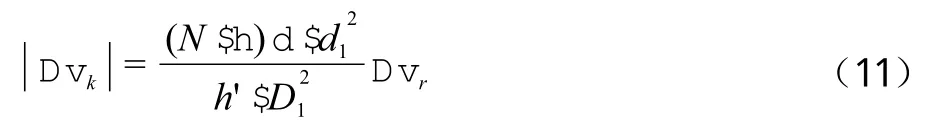
式中:D1——管桩桩径;
d1——小孔孔径;
δ——管桩壁厚;
h'——小孔竖向间距;
N——开孔数量;
η——小孔的布置方式。
选取应力函数:φ =A·z2lnr +B·zlnr(A、B为系数),代入d4φ =0,则有孔管桩沉桩过程中弹性区产生的应力增量为:
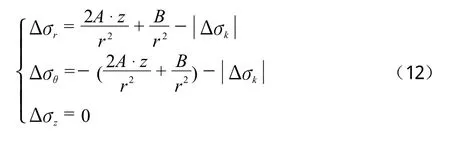
在弹性区和塑性区交界处(r =Rp)应力连续,解得:

式中:k0——静止土压力系数;
γ——土的重度;
c——土的黏聚力。
代入式(1)可得在考虑深度z的影响下,弹性区有孔管桩超孔隙水压力消散规律与深度之间的关系式:
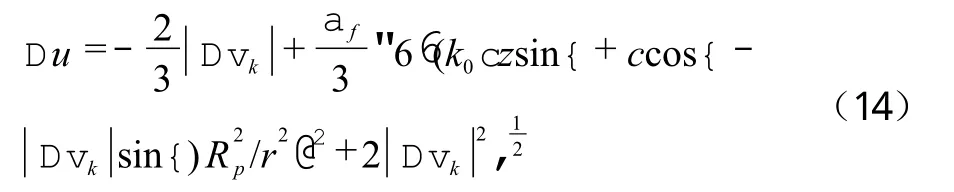
2.3.2 塑性区有孔管桩超孔隙水压力空间解析解
随着桩侧土体进入塑性区,塑性区土体满足Mohr-Coulomb屈服准则[8]:
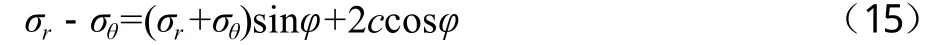
将式(15)代入静力平衡方程,根据应力边界条件可以解得无孔管桩塑性区的应力增量。考虑到桩身开孔,可以推导出有孔管桩沉桩过程中塑性区产生的应力增量公式。
由于桩顶填土可看作是无限均布荷载作用,桩侧顶部侧向压力P0即为土体的初始应力q0,即:
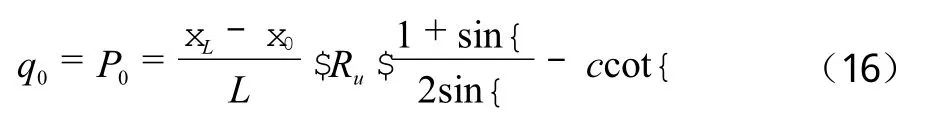
式中:Ru——圆孔扩张后的最终半径,即桩体半径。
通过计算可得:

将式(4)、(5)和(17)代入公式(1)中,可以得到在考虑深度的影响下,有孔管桩沉桩塑性区超孔隙水压力解析解:
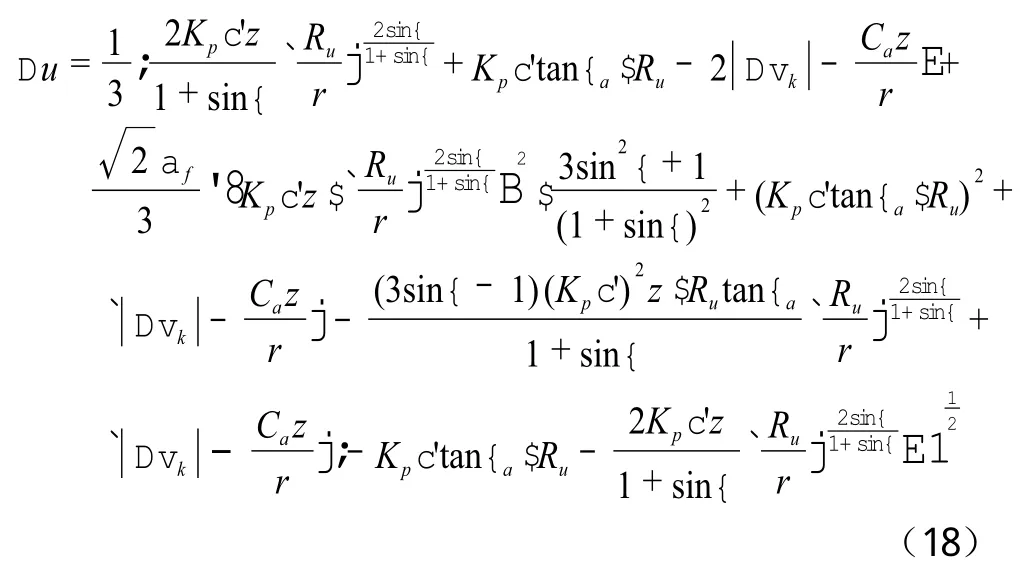
从公式(14)、(18)可以看出,超孔隙水压力值与径向距离、深度均有关系,这与最初的设想是吻合的。为了验证解析式的准确性,将引入工程实例来进一步分析超孔隙水压力与径向距离、深度之间的关系。
3 算例分析
在某软黏土地区进行有孔管桩的静压沉桩,在管桩相同高度平面内等角度开3个小孔,桩长8.0 m,桩径d=0.4 m,管桩壁厚3mm,桩身开孔竖向间距1.0 m,其他基本参数如下:E=3.0×103kPa,μ=0.5,Cu=20 kPa,c=10 kPa,Ca=12 kPa,φ=15°,φa=20°,Ru=0.3 m,土的重度为18.1 kN/m3,γ'=8.1 kN/m3,取αf=0.87,开孔孔径取d1=0.08 m,体积影响系数Vk=0.01 m2。
3.1 同一深度下超孔隙水压力与径向距离之间的关系
选取3处不同的深度z,得到同一深度时Δu与r之间的关系(图1)。

图1 不同的深度下超孔隙水压力Δu与径向距离r之间的关系
分析图1可以得到:对于同一深度处的不同径向距离,超孔隙水压力随着径向距离的增大而减小。
3.2 同一径向距离下超孔隙水压力与深度之间的关系
选取3处不同的径向距离r(d为桩径),得到同一径向距离时Δu与z之间的关系(图2)。
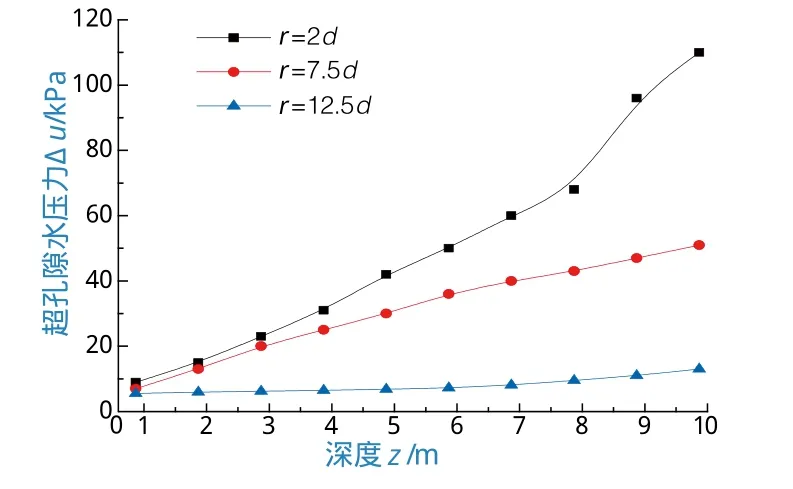
图2 同一径向距离下超孔隙水压力Δu与深度z之间的关系
分析图2可以得到:对于同一径向距离处的不同深度,超孔隙水压力随着深度的增加而增大。
3.3 超孔隙水压力与径向距离、深度的关系
综合图1、图2,可得到超孔隙水压力与径向距离和深度之间的三维关系(图3)。
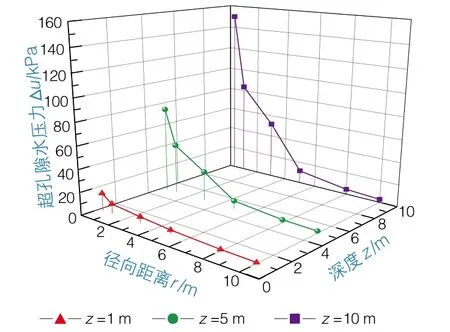
图3 超孔隙水压力Δu与深度z、径向距离r的关系
分析图3可得:不论是弹性阶段还是塑性阶段,当径向距离r确定时,在一定范围内超孔隙水压力随深度的增加呈线性递增,当确定深度z时,超孔隙水压力将随着径向距离的增大而减小;对比弹性区与塑性区发现,弹性区超孔隙水压力远小于塑性区超孔隙水压力。计算结果与理论公式分析基本吻合,说明理论计算公式具有一定的合理性。
4 数值模拟
4.1 基本假定
为了能够更精确地模拟沉桩过程,获得更准确的数据,作如下假定[9]:
1)考虑到实际沉桩的复杂性,作出合理简化。
2)桩体采用离散刚体模型,桩身材料选择钢筋混凝土。
3)桩周土体为符合M-C屈服准则的均匀理想弹塑性体。
4)桩-土接触面采用摩擦类型为库仑摩擦的面-面接触方式,同时认为桩体和周围土体一旦接触就不再分开,只发生切向的相对滑动。
5)土颗粒和孔隙水不可压缩,发生体积变化是由颗粒间的孔隙被挤压造成。
6)沉桩过程中,忽略桩周土的固结,同时不考虑开孔处的应力增量及渗透系数随竖直方向的变化。
4.2 有限元计算模型
本章选取星状对穿孔管桩,即在管桩同一截面开3个孔,3个孔的孔心成等边三角形(图4)。
本章土体选取的计算区域自地表垂直向下16 m,水平面为一个边长为16 m的正方形,模型大小为16 m×16 m×16 m。现取有孔管桩半径为0.2 m,管桩壁厚3mm,桩侧开孔直径8 cm,桩长8 m,竖向开孔间距选择1.0 m,模拟管桩从地表直至贯入到土体内部的过程(图5)。
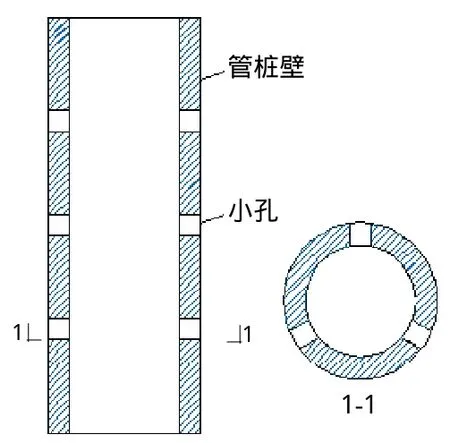
图4 星状有孔管桩结构示意

图5 有限元模型
本章不考虑桩尖进入土体对土体的扰动变形,假定管桩进入土体后的扩张过程为圆柱孔的扩张,通过施加在桩顶的竖向位移荷载和孔壁处竖向摩擦力,来模拟管桩在土体的沉桩和超孔隙水压力的产生、消散过程。设置有限元模型上表面为自由面,下表面和4个侧面均固定。对有孔管桩的超孔压采用渗流模式进行计算,设置单元为各向同性渗流模型。土体上表面可自由排水,孔隙水还可从桩土界面及桩身小孔排出。
4.3 径向距离对超孔隙水压力的影响
4.3.1 计算参数的设定
z取1、5、10 m,E取3.06 MPa,μ取0.45,γ取18.1 kN/m3,c取10.6 kPa,摩擦角φ取16.1°,渗透系数k取5.8×10-4m/d,初始孔隙比e取1.5。
4.3.2 超孔隙水压力随径向距离的变化规律
由沉桩完成后超孔压沿径向分布(图6)可知,相同深度处超孔压值随径向距离的增大总体上呈衰减趋势。

图6 沉桩结束时超孔压Δu随径向距离的变化曲线
4.4 深度对超孔隙水压力的影响
为了更深入地模拟深度变化对超孔压的影响,分别选择了沉桩过程中和沉桩完成后这2种工况来反映超孔压的消散规律。第1种是沉桩过程中,距桩心距离r=2d处,当桩贯入不同深度(2、4、6、8 m)时超孔隙水压力沿深度的分布情况;第2种情况是沉桩结束,距桩心轴线不同距离(r=2d、7.5d、12.5d)处的超孔压的变化规律。
4.4.1 距桩心轴线2d处超孔隙水压力的变化规律
桩体沉桩过程中,深入土体不同深度时的超孔压大小不同(图7)。在整个桩体贯入过程中,孔隙水压力自土体表面到桩端逐渐增大至最大值。在这过程中,超孔压的最大值出现在桩端部位,且随着桩的贯入而逐渐增大。

图7 距桩2d处超孔压随深度的变化曲线
4.4.2 距桩心轴线不同距离处超孔隙水压力的变化规律
沉桩结束后,距桩中心不同径向距离处超孔压随深度的增加,其值总体上呈逐渐增加的趋势(图8)。
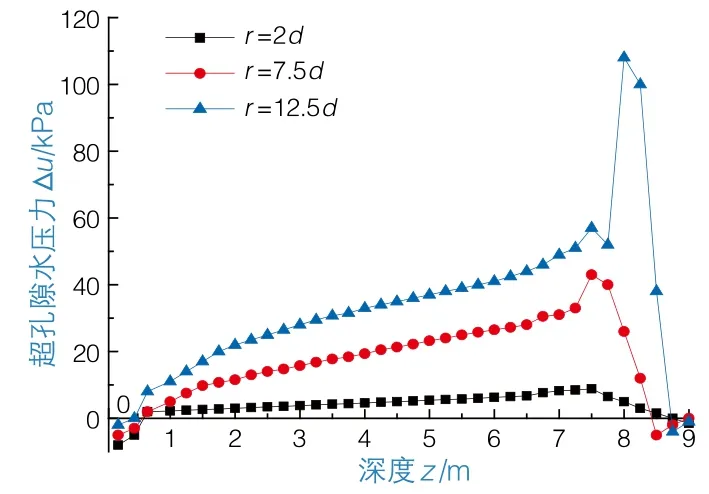
图8 沉桩结束时超孔压随深度的变化曲线
沉桩完成后,地表周围的水压力会出现负值,产生负压力主要是因为此区域范围内土体受到桩体挤压向上隆起造成的。
4.5 理论推导与数值模拟对比分析
4.5.1 超孔隙水压力与径向距离之间关系的对比
通过对比有孔管桩静压沉桩过程中超孔压随径向距离变化的理论值与模拟值,得到超孔隙水压力与径向距离之间的变化曲线(图9)。
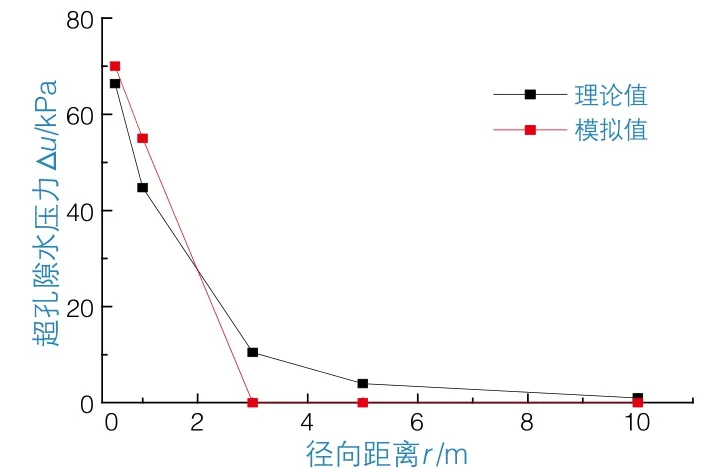
图9 超孔隙水压力与径向距离之间变化规律的对比
由图9可知:超孔隙水压力的理论值和模拟值随径向距离的变化趋势基本一致。随着径向距离的增大,超孔隙水压力逐渐减小,离桩心越近,超孔压衰减越快;在理论分析过程中,对沉桩过程作了一定的简化和合理的假设,因此求得的超孔隙水压力最大理论值比最大模拟值要小;且有孔管桩静压沉桩产生的超孔隙水压力的主要影响范围为8d,超过这个范围,桩周土体内的水压力变化不明显。
4.5.2 超孔隙水压力与深度之间关系的对比
为了对比超孔压理论值和模拟值与深度的变化关系,选择了3种不同深度(z=1、5、10 m),根据有孔管桩静压沉桩过程中超孔压随深度变化的理论值与模拟值,得到超孔隙水压力与深度之间的变化曲线(图10)。
分析图10可知:超孔隙水压力的理论值和模拟值随深度的变化趋势总体上基本一致;相同深度处,随着径向距离的增大,超孔隙水压力逐渐减小。
由于对理论分析过程作了一些简化和假定,超孔隙水压力的最大理论值比最大模拟值要小,同时通过数值模拟得到的超孔压值随径向距离消散得更快,且其主要影响范围为8d。
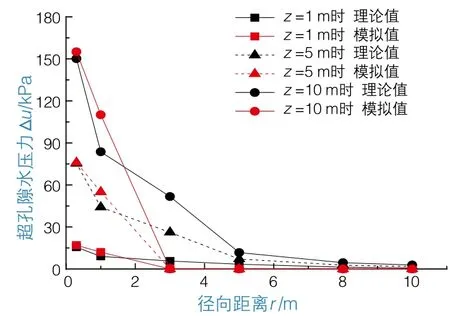
图10 超孔隙水压力与深度之间变化规律的对比
5 结语
1)基于圆孔扩张理论,根据传统无孔管桩沉桩超孔隙水压力的三维解析解,得到有孔管桩的空间应力解,推导出有孔管桩扩张过程中桩周土体的弹塑性区超孔隙水压力的空间解析式。
2)同一深度处,有孔管桩超孔隙水压力随径向距离的增大而减小;相同径向距离处,超孔压随深度的增加而增大。
3)通过对比分析理论计算与数值模拟的结果,验证了本文理论公式具有一定的合理性。
4)由于假定存在缺陷,推导出的静压有孔管桩超孔隙水压力最大值比实际的超孔隙水压力小,需要进一步考虑相关系数以修正表达式。

