MCMA盲均衡算法的FPGA高效实现

李淑婧 王蕾 张东伟 张帆

关键词： 修正恒模算法; QPSK信号; 高时钟; 流水线结构; 乘法器复用; 盲均衡

中图分类号： TN919?34                          文献标识码： A                         文章编号： 1004?373X（2019）01?0009?05

Abstract： The modified constant modulus algorithm （MCMA） acts as an efficient blind equalization algorithm for QPSK signal. The blind equalization algorithm using MCMA was implemented by adopting pipeline architecture on Artix?7 series XC7A200T?2SBG484 chip， and combining the modes of high clock and multiplier reuse. The restrictive relationship between step parameter and algorithm performance is verified， and the optimized step parameter is selected. On the premise of guaranteeing the bit error rate and convergence speed of the algorithm， the implementation complexity of algorithm is reduced effectively， and the satisfied equalization effect is realized with less hardware resources. The data collected from the flight test is applied to the equalizer. The verification results show that the equalizer with less hardware resources can achieve high performance， and the demodulation signal?to?noise ratio of the receiving end is reduced by 4 dB.

Keywords： modified constant modulus algorithm; QPSK signal; high clock; pipeline architecture; multiplier reuse; blind equalization

0  引  言

在無线通信信号传输过程中，有限的传输带宽，多径效应，以及加性噪声等因素导致接收端在数据抽样时产生符号间干扰，从而降低了信号的传输效率和传输质量[1]。信道均衡可以消除符号间干扰和补偿信道失真，从而降低误码率，提高通信质量。

早期的自适应均衡算法需要在发送端的帧结构中插入训练序列，以便实时跟踪信道特性变化，但如此会降低信道频谱利用率，浪费带宽资源[2]。相比之下，盲均衡算法不需要发送训练序列，仅利用发送信号的特征进行均衡，此特性使其成为通信领域的研究热点。几十年以来，针对不同的应用需求，研究者进行了大量卓有成效的研究，进而提出了多种盲均衡算法，其中最具代表性的是Godard算法[3]。当代价函数的阶数取2时，得到Godard算法的一个特例——恒模算法（Constant Modulus Algorithm，CMA）[4]。CMA算法具有结构简单、易于实现、稳定性好等优点，是一种较为常用的均衡算法。但CMA算法只考虑了信号的幅度信息，没有考虑相位信息，因此该算法存在收敛速度慢、计算量大、无法克服相位失真等缺点[5]。文献[6]提出修正恒模算法（Modelfied Constant Modulus Algorithm，MCMA），该算法将输入信号分为I，Q两路进行均衡，在均衡过程中能够有效克服相位失真问题，提高了CMA算法的性能。同时，对于信道的快速变化引起载波相位不稳的问题，MCMA也能够对其进行恢复。

随着现场可编程逻辑门阵列（FPGA）技术的发展，芯片集成度越来越高，但是其功耗以及成本在不断下降，以及FPGA开发软件的功能不断完善，使得其在信号处理领域得到越来越多的应用，基于System Generator for DSP 开发软件在FPGA上可以实现MCMA信道均衡器的设计，并利用Simulink给出对均衡器进行仿真测试验证的结果[7]。

本文基于FPGA实现了MCMA均衡算法，所设计均衡器已被某实装航空通信系统采用并经实测提升了性能。首先介绍了MCMA算法的基本原理，然后将试飞时采集接收的信号作为数据源在Matlab平台上验证MCMA均衡器的性能并详细分析了影响均衡性能的步长参数的选取方法;其次对MCMA算法的FPGA实现方案进行了详细介绍。

MCMA算法包含大量的乘法以及平方运算，并且是I，Q两路，因此采用FPGA内部硬件资源实现此算法需要消耗大量的乘法器IP核，从而限制了该算法的应用范围。针对该问题，本文在实现MCMA算法过程中采用串行流水线结构和乘法器复用的方式，节约了硬件资源并达到了较好的均衡效果。最后通过试飞实测结果验证了所设计均衡器的优良性能，接收信号经过设计的均衡器处理后，通信解调信噪比下降了4 dB。

由式（11）可知，MCMA将均衡器输入信号分为实部和虚部，也就是将复数运算简化为实数运算，即转换为信号的幅度和相位信息，有效降低了计算复杂度，便于硬件实现。系数更新公式中实部和虚部同时需要做乘法运算，在信道估计出均衡器系数以后真实信号通过均衡器也需要做乘法运算，这样整个均衡器的乘法运算量过大，若采用乘法器IP核来实现，导致占用硬件资源过多，故在实现过程中乘法器复用，并采用高时钟流水线结构，这样可以节省硬件资源并达到均衡效果。

1.3  MCMA验证与性能分析

为了验证MCMA的有效性以及算法性能与关键参数的关系，将试飞采集到的数据作为信源数据，在Matlab平台上验证MCMA算法的均衡效果以及分析算法收敛速度、稳态误差与步长[μ]的关系。

均衡器采用16阶横向抽头结构，中心抽头系数初始化为1，其他抽头系数初始化为0，信道的冲击响应为[1，0.5，0.35，0.2]，调制方式为QPSK，[EbN0]为20 dB。对于QPSK调制信号，相应的[Rm]值为[2.097  2×106]。

若步长[μ]设置较小，虽然收敛效果很好但是收敛的速度却很慢;若步长[μ]设置较大，虽然收敛速度加快但是稳态误差较大，会导致误码率性能下降，通过调整步长[μ]使系统的均衡性能达到最优[9]。

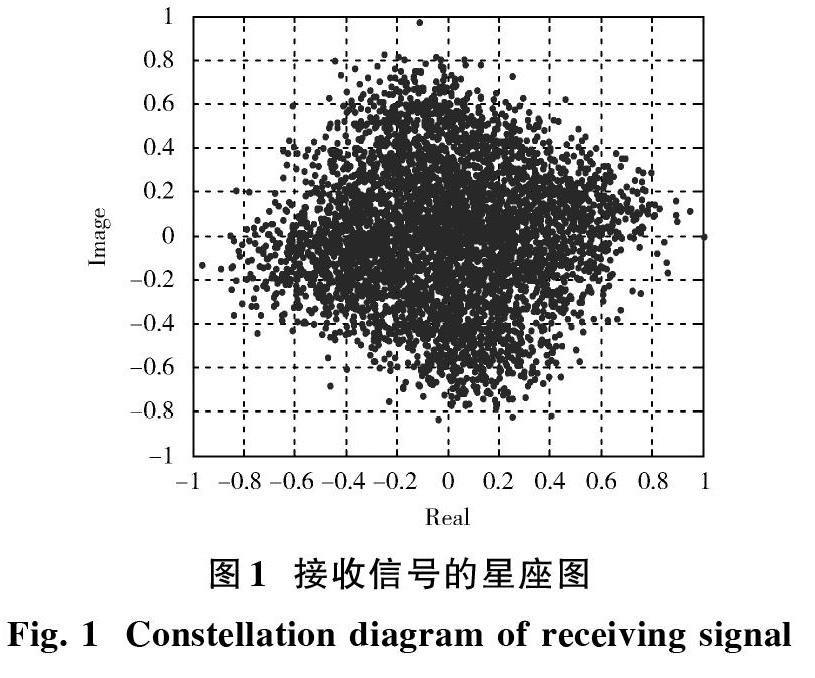
为了验证均衡器的性能，在相同的信道仿真环境下，采用不同步长[μ]的均衡器输出信号星座图，误差信号、权值收敛也进行对比分析选出最优的步长参数。均衡器输入信号星座如图1所示。

由图1可知，接收到的信号幅度和相位均产生了失真，QPSK信号的相位不再集中在4个相位点上，无法辨认出原始的星座图。

接收信号通过均衡器后的星座图如图2所示，均衡器输出信号的相位大致集中在4个相位点上，可知此均衡器可以纠正信号的相位失真，图2a）采用步长[μ]=[27]，图2b）采用步长[μ=210]，显然，采用步长[μ]=[210]输出信号的星座点更加紧簇。

均衡误差值波动如图3所示，其中步长[μ]=[210]的波动范围比[μ]=[27]小。

均衡器权值收敛如图4所示，实线为[μ]=[27]权值系数变化曲线，虚线为[μ]=[210]权值系数变化曲线，很显然权值系数经过不断更新后可以收敛，但[μ=210]的收敛速度比[μ]=[27]快。

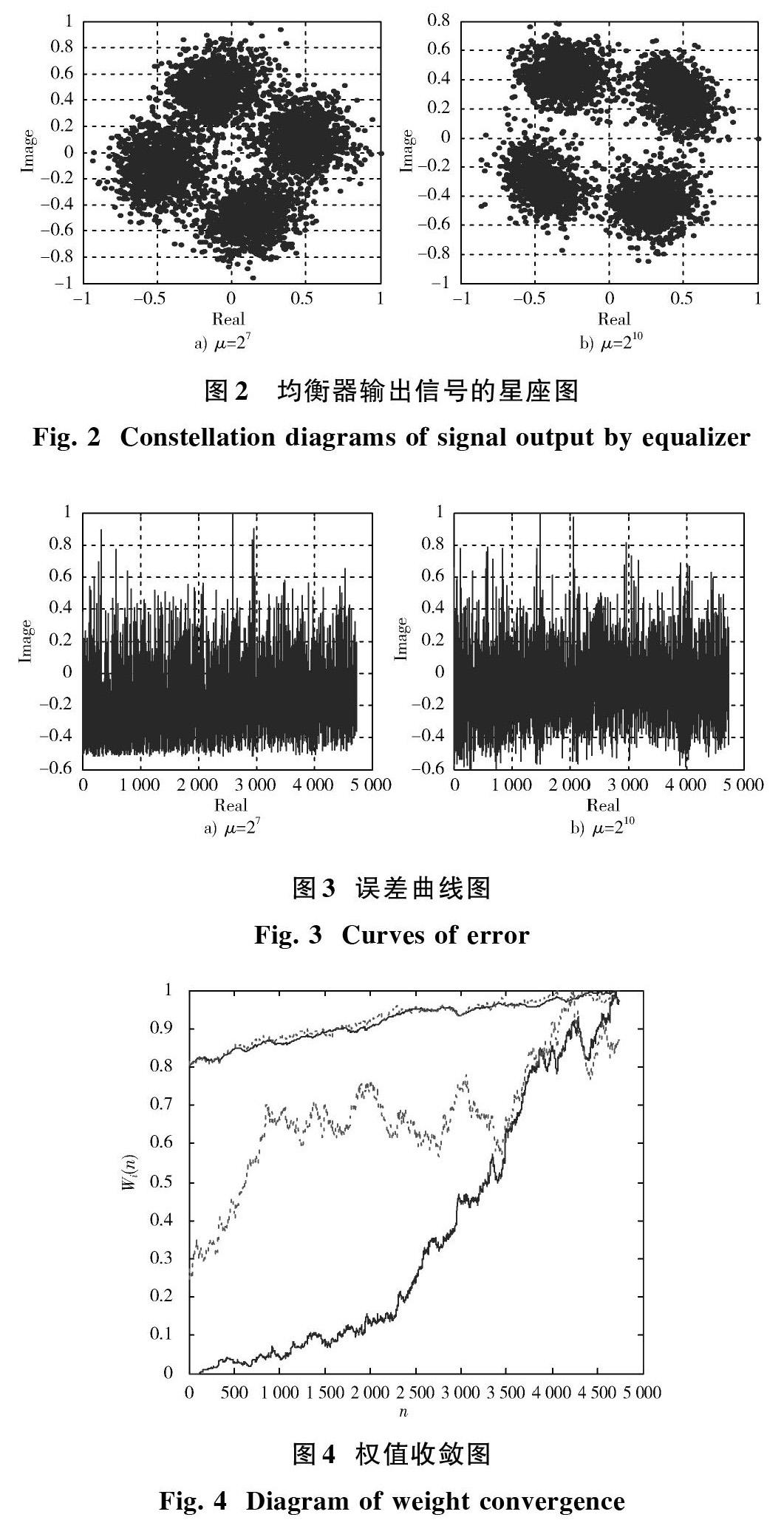
当步长[μ]较大超出范围则算法不收敛，所以步长的选择是影响算法的一个关键[9]。从采用不同步长后的均衡效果来看，为了降低均衡信号的相位失真，此均衡器采用步长[μ=210]。

2  MCMA的FPGA实现

本文均衡器采用硬件描述语言VHDL在Xilinx公司的ISE14.7环境下编程实现，将试飞采集到的数据以.txt文件存储，在ModelSim中读取.txt文件作为接收信号源。均衡器采用的FPGA是Xilinx公司的Artix?7系列的XC7A200T?2SBG484，此芯片相对于Spartan?6系列而言，成本降低但是容量却提高2倍以上，而且内部740个DSP模块可用于复杂计算。

本文设计的MCMA盲均衡器结构框图如图5所示。均衡器主要由归一化模块、抽样模块、滤波器模块、误差计算模块、权值调整模块以及均衡数据存储模块组成[10]。

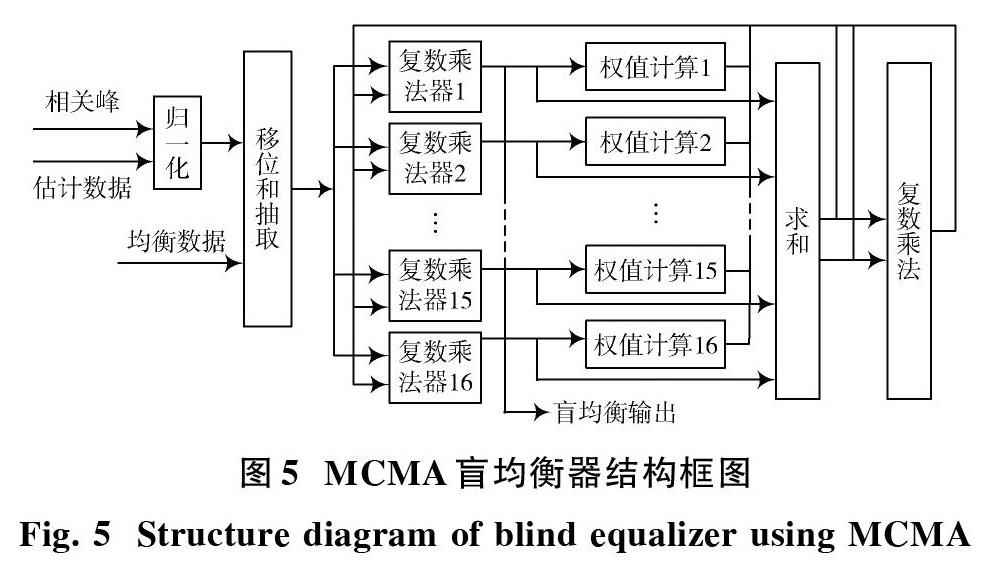
均衡器输入的估计数据并行作为两个模块的输入，一个作为内部RAM存储，另一个用于估计均衡器系数，待估计出系数后再启动RAM的读使能，对存储信号进行均衡。

2.1  各子功能模块实现方法

2.1.1  归一化模块

为了保证均衡器输入信号幅度的平稳性，首先对信号进行归一化处理。接收信号通过捕获模块得到的相关峰值作为归一化子模块输入，输入的I，Q兩路信号都是16 bit，十进制数表示最大值为32 767，本设计将信号的幅度量化为（-16 384，16 383）之间，使均衡器输入信号的模值范围固定，便于算法的收敛。

2.1.2  抽样模块

主时钟设为采样时钟的2倍，输入的I，Q信号每个码元由8个采样点组成，均衡滤波器权值更新过程中每个码元抽取两个采样点，作为后续均衡器处理数据。此模块的关键点就是对码元信号进行均衡过程中由于采用高时钟可以在码元周期内串行完成后续滤波器乘累加运算。

2.1.3  滤波器模块

滤波器是均衡器的核心单元，采用判决反馈结构，其主要功能是将均衡器的输入信号与均衡器的权值系数进行卷积操作。滤波器卷积运算中两个复数矩阵的乘法运算采用IP核实现，提高运算的速度。1个16 bit乘法器需要3个DSP block单元，1个16阶的滤波器就需要使用96个DSP单元，这样乘法器占用资源太多，因此采用复用的方式，有效地降低硬件资源消耗。本文均衡器采用的时钟是61.44 MHz，码元速率为3.84 MHz。将码元抽取的采样信号存入缓存移位数组，ES_Din（[n]），[n=]0，1，2，…，15，并开始计数。每个时钟上升沿，当前系数与缓存中的数据作一次复数乘法得到ES_i（[n]），ES_q（[n]），由前一个系数减去ES_i（[n]），ES_q（[n]），输出的结果即当前权值系数，再将其反馈为复数乘法器的输入，此前向滤波器完成均衡器输入信号[x（k）]与反馈系数[w（k）]之间的乘积，同时实现抽头系数的更新：[w（k+1）=w（k）-μ?e（k）x（k）]，如图5所示，权值计算输出反馈到复数乘法器的输入。

后向滤波器主要实现均衡器输出信号[y（k）]经过判决后与反馈系数[w（k）]之间的乘积，同时更新反馈系数。在进行输入信号[x（k）]与反馈系数[w（k）]的卷积运算时，由于实现中的乘法、加法运算存在一个时钟的延迟，在得出误差函数[e（k）]后，采用高时钟流水线的方式保证反馈系数更新公式中的[μ?e（k）x（k）]能进行正确运算。

2.1.4  误差计算模块

误差计算是算法的核心，如图5所示采用权值计算模块的输出求和后的[y（k）]包含I，Q两路信号计算误差函数[e（k）]，首先经过复数乘法模块实现平方运算，再与[R2，R]做差运算，最后与[y（k）]进行乘法运算。

根据反馈误差值[e（k）]及输入信号[x（k）]完成滤波器权值系数的更新，为了节约硬件资源，步长因子[μ]在本文设计中取[210]，因此可以采用移位操作实现乘法运算。此均衡过程在高时钟下经过一个码元周期便可实现反馈系数的一次更新。

2.1.5  均衡真实数据

估计数据经过滤波器的系数反馈后，就可以得出最终的权值系数，此时再将存储的信号存入缓存移位数组，再次经过滤波器前向滤波以后的结果就是信号均衡后的输出结果。

综上所述，为了工程实现的需要，本文设计做了适应性改进，系统采用高时钟，在一个码元周期内采用串行流水线的方式处理，即一个码元周期内高时钟进行计数，按照计数器值分解滤波器的乘累加运算步骤，保证数据的正确运算;由于反馈系数调整采用流水线的方式，故乘法器可以复用，节约硬件资源。

2.2  实测数据验证

本文设计的盲均衡器在FPGA实现过程中，需要注意的问题是时序、数据位宽、信号溢出、数据存储、数据移位、均衡处理速度等问题。处理时序用一个模8计数器，在一个采样周期内串行完成一次数据的更新;在数据位宽方面，由于每一次乘法运算结果的数据位宽是两个相乘数据位宽的和，直接采用乘法器输出结果进行后续的计算会占用较多资源，所以要对乘法器的输出结果进行适当的截位处理;针对信号溢出问题，本次均衡器的输入采用归一化处理后的数据;运算时，为了便于实现数据乘法，设置步长值为[2n]，这样就不必使用乘法器，将乘法运算转变为数据移位操作，从而节省了资源。

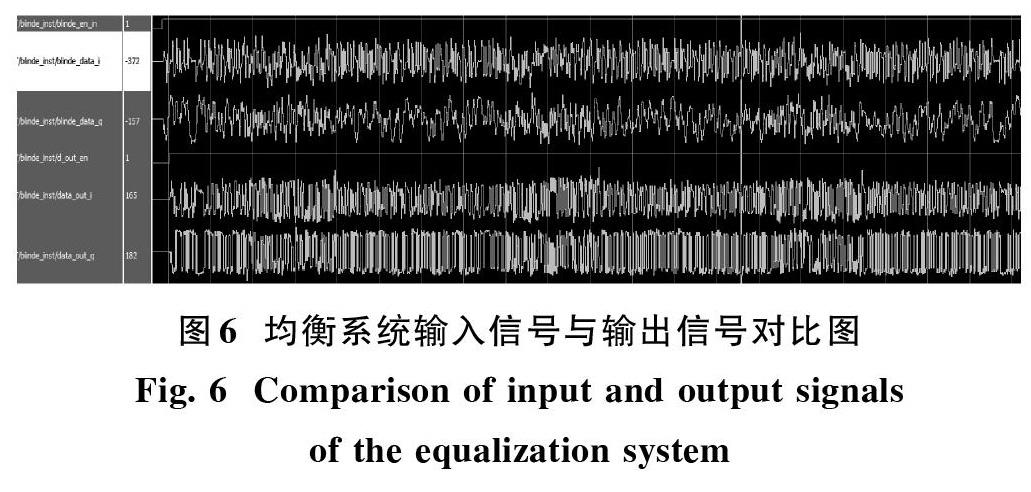
均衡器的输入和输出信号对比如图6所示，其中blinde_en_in，blinde_data_i，blinde_data_q分别为本均衡器的启动使能，均衡器输入信号的实部，均衡器输入信号的虚部，显然，输入信号波形所携带的相位已经严重失真，data_out_i，data_out_q分别为均衡器输出信号的实部，均衡器输出信号的虚部，经过均衡器后纠正了信号的相位失真，信号的幅值波动不大。

算法的收敛速度验证如图7所示，盲均衡算法的收敛速度直接影响工程的实现，是判断盲均衡性能极其重要的指标，收敛速度是指从均衡器开始工作到算法收敛所需的迭代次数。

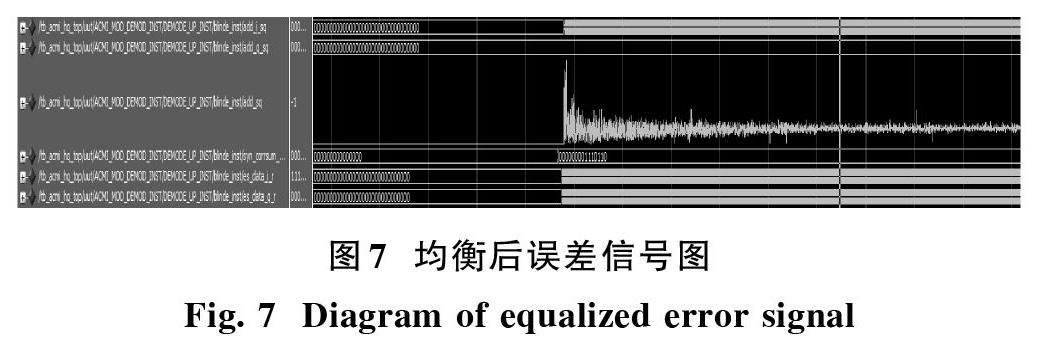
图7中add_sq为均衡后误差信号，开始时，误差值比较大，随着迭代次数的增加，误差值的改变也较快，当进入收敛状态后，误差值便在某一数值附近波动，表明该均衡器可以实现。这样就不必使用乘法器，将乘法运算转变为数据移位操作，从而节省了资源。

在某通信系统试飞试验中，加入此均衡器设计以后，弹载通信端机能与地面站进行正常的收发通信交互，分析弹道仿真机采集数据显示，该端机在空域内能收到其他端机数据，在相同的飞行条件下，将弹载端机采集数据进行分析，结果表明相同的误码率条件下地面接收终端通过频谱仪测得的信号值比没有均衡器设计的要小4 dB。

3  結  语

本文基于FPGA设计实现了一种适用于QPSK信号的盲均衡器，通过合理选择步长[μ]值，滤波器的权值系数更新过程采用流水线设计以及乘法器复用，将滤波器乘累加计算在高时钟下按照计数器值分步骤进行，保证数据的正确运算。由于采用流水线的架构，误差迭代计算中的乘法计算所调用的IP核可以复用，节约了片内的乘法器资源，实现了均衡效果和占用硬件资源的平衡。通过Matlab平台验证表明，此次设计的均衡器可实现较好的均衡效果。通过某在研的通信系统试飞，也表明均衡器的有效性。

参考文献

[1] SKLAR B.数字通信：基础与应用[M].2版.徐平平，译.北京：电子工业出版社，2002：173?182.

SKLAR B. Digital communications fundamentals and applications [M]. 2nd ed. XU Pingping， Translation. Beijing： Publi?shing House of Electronics Industry， 2002： 173?182.

[2] OH K N， CHIN Y O. Modified constant modulus algorithm： blind equalization and carrier phase recovery algorithm [C]// Proceedings of 1995 IEEE International Conference on Communications. Seattle： IEEE， 1995： 498?502.

[3] GODARD N. Self?recovering equalization and carrier tracking in two?dimensional data communication systems [J]. IEEE tran?sactions on communications， 1980， 28（11）： 1875?1886.

[4] LEE L. A modified blind equalization technique based on a constant modulus algorithm [C]// 1998 IEEE International Conference on Communications. Atlanta： IEEE， 1998： 344?348.

[5] 张丹丹.盲均衡算法及其FPGA实现的研究[D].秦皇岛：燕山大学，2013：20?21.

ZHANG Dandan. Research of blind equalization algorithm and its FPGA implementation [D]. Qinhuangdao： Yanshan University， 2013： 20?21.

[6] JIANG Zhixiang， ZHANG Meng， LI Zichuang， et al. A newly high?speed MCMA algorithm for QAM system [C]// The 4th International Conference on Wireless Communications， Networ?king and Mobile Computing. Dalian： IEEE， 2008： 1?4.

[7] 钱小云，白勇博，田兆平，等.基于System Generator的MCMA算法盲均衡器的FPGA实现[J].江苏科技信息，2016，6（18）：54?56.

QIAN Xiaoyun， BAI Yongbo， TIAN Zhaoping， et al. The FPGA implementation of MCMA blind equalizer based on system generator [J]. Jiangsu science & technology information， 2016， 6（18）： 54?56.

[8] RAO Wei， ZHANG Xingwang. New concurrent blind equalization algorithm suitable for high?order QAM signals [C]// The 5th International Conference on Fuzzy System and Knowledge Discovery. Shandong： IEEE， 2008： 177?181.

[9] 郝放，闵洁，孙志远.基于MCMA的盲均衡算法[J].无线电通信技术，2014，40（1）：41?43.

HAO Fang， MIN Jie， SUN Zhiyuan. Blind equalization algorithm based on MCMA [J]. Radio communication technology， 2014， 40（1）： 41?43.

[10] 吳迪，霍亚娟，葛临东，等.高阶QAM信号盲均衡算法及其FPGA实现[J].计算机工程，2010，36（15）：233?239.

WU Di， HUO Yajuan， GE Lindong， et al. Blind equalization algorithm of high?order QAM signal and its FPGA?based implementation [J]. Computer engineering， 2010， 36（15）： 233?239.

[11] 朱振超，梁广真.一种新型变步长CMA盲均衡算法[J].现代电子技术，2014，37（18）：56?58.

ZHU Zhenchao， LIANG Guangzhen. A new variable step?size CMA blind equalization algorithm [J]. Modern electronics technique， 2014， 37（18）： 56?58.

[12] ASHMAWY D， BANOVIG K， RAHEEM E A， et al. Joint MCMA and DD blind equalization algorithm with variable?step size [C]// 2009 IEEE International Conference on Electro/Information Technology. Windsor： IEEE， 2009： 174?177.