西湖凹陷超压预测方法研究

陈军军

(西安石油大学 地球科学与工程学院,西安 710065)

西湖凹陷位于东海陆架盆地的东北部，呈NNE向展布.主要受东侧的西湖-基隆大断裂控制，凹陷中段受西部平湖主断裂控制，具有一定的的双断结构；后期受构造反转作用影响，在凹陷中央发育一系列大型反转背斜，凹陷总体上可以划为西部斜坡带、中央-洼陷反转构造带和东部断阶带.根据已研究资料可以知道，西湖坳陷的异常高压主要以生烃增压为主[1].但就一个特定异常压力体而言，其成因可能以某一种因素为主，其它因素为辅.其中，泥岩欠压实和生烃增压两种成因最为常见.

1 Fillippone法

刘震(1990)通过对辽东湾辽西凹陷的压力测试资料的分析发现，地层压力与速度呈对数关系，于是他将Fillippone公式[2]修正为：

云美厚[3](1993)在二式中分别引入一个随速度变化的校正系数，得到如下两个预测方程：

式中，FC(V)、LC(V)分别为速度校正系数.

由图1可知，地层压力与Ln(V)的相关性比V的相关性更好.

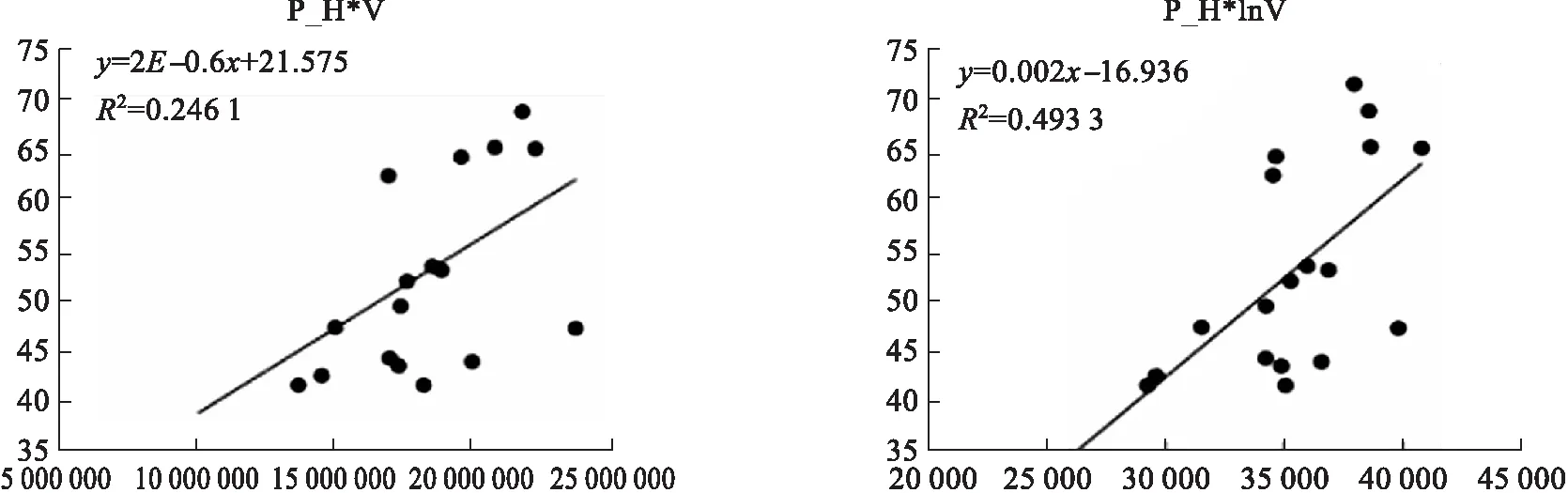
图1 地层压力与Ln(V)及V的相关性比较

从Fillippone法经过云美厚的修改以后，预测精度得到了提高，而且可以看出云美厚法压力预测精度高出许多，相对误差达到4.08左右，由表1可见：在西次凹及中央反转构造带会出现云美厚法比Fillippone法预测误差稍大的情况，这可能与在西次凹及中央反转构造带的数据太少，出现误差过大的情况有关.由表2可见，总体上从西斜坡来看，改进Fillippone法(云美厚法)的压力预测精度比Fillippone预测法高.

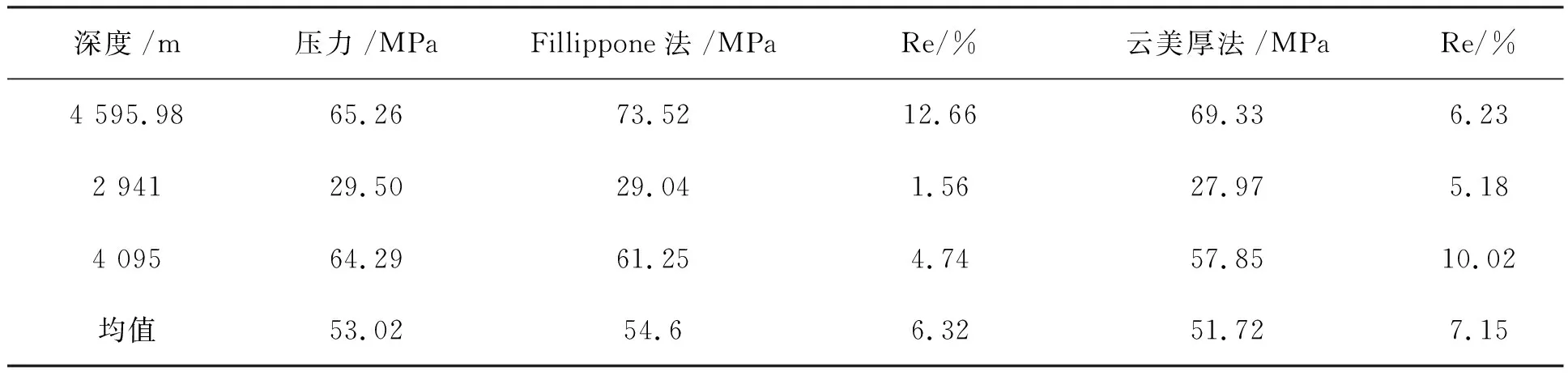
表1 西次凹及中央反转构造带Fillippone法与云美厚法压力预测对比表(测线1)

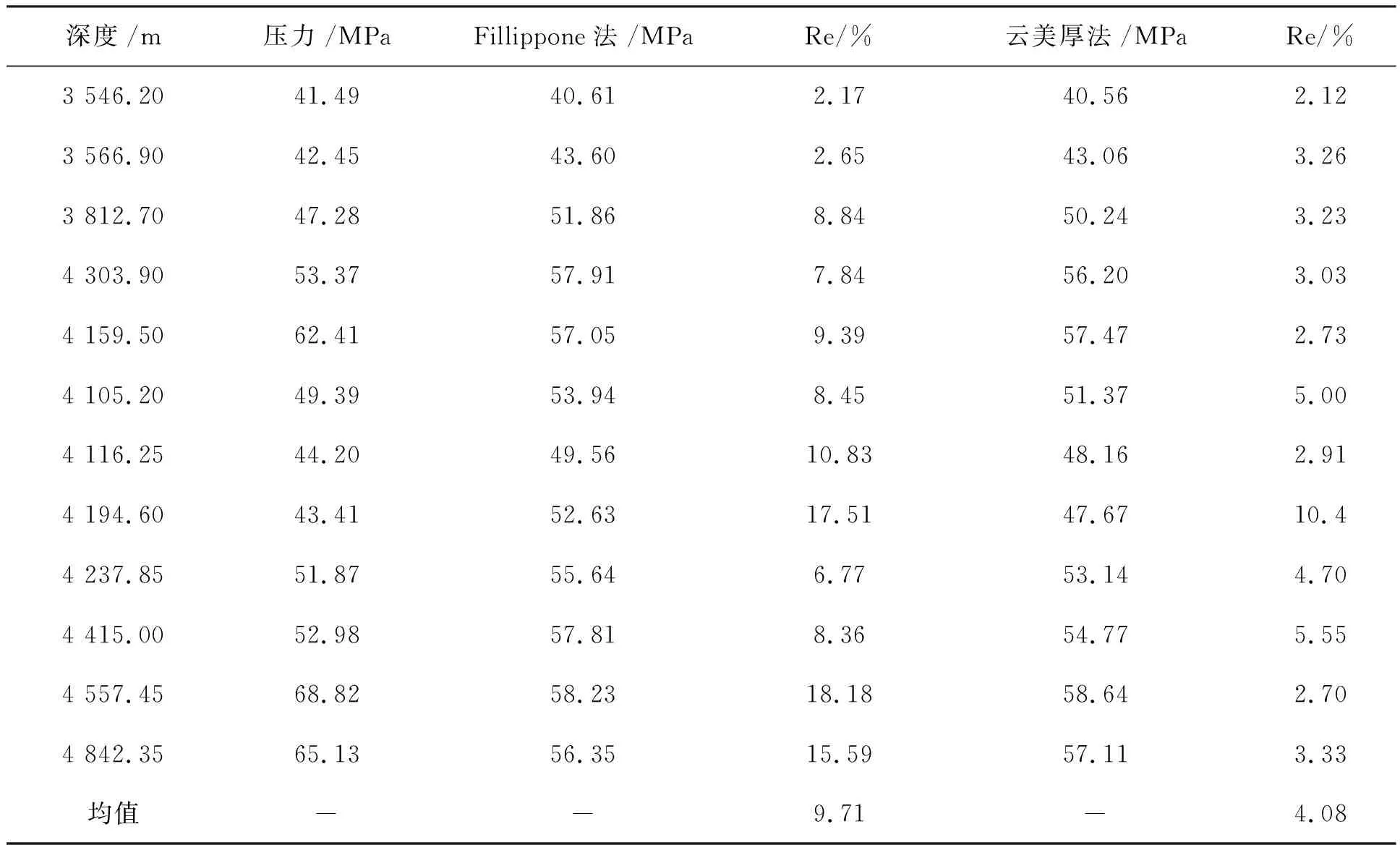
表2 西斜坡Fillippone法与云美厚法压力预测对比表(测线1)

2 Eaton法

伊顿法[4]预测压力公式：

其中：Pp为预测地层压力；S为上复地层压力；Ph为静水压力Δtn为正常压实情况下地震速度倒数，或旅行时；Δto为实测地震速度倒数，或实测旅行时；N为伊顿指数，需根据工区情况，试验确定.

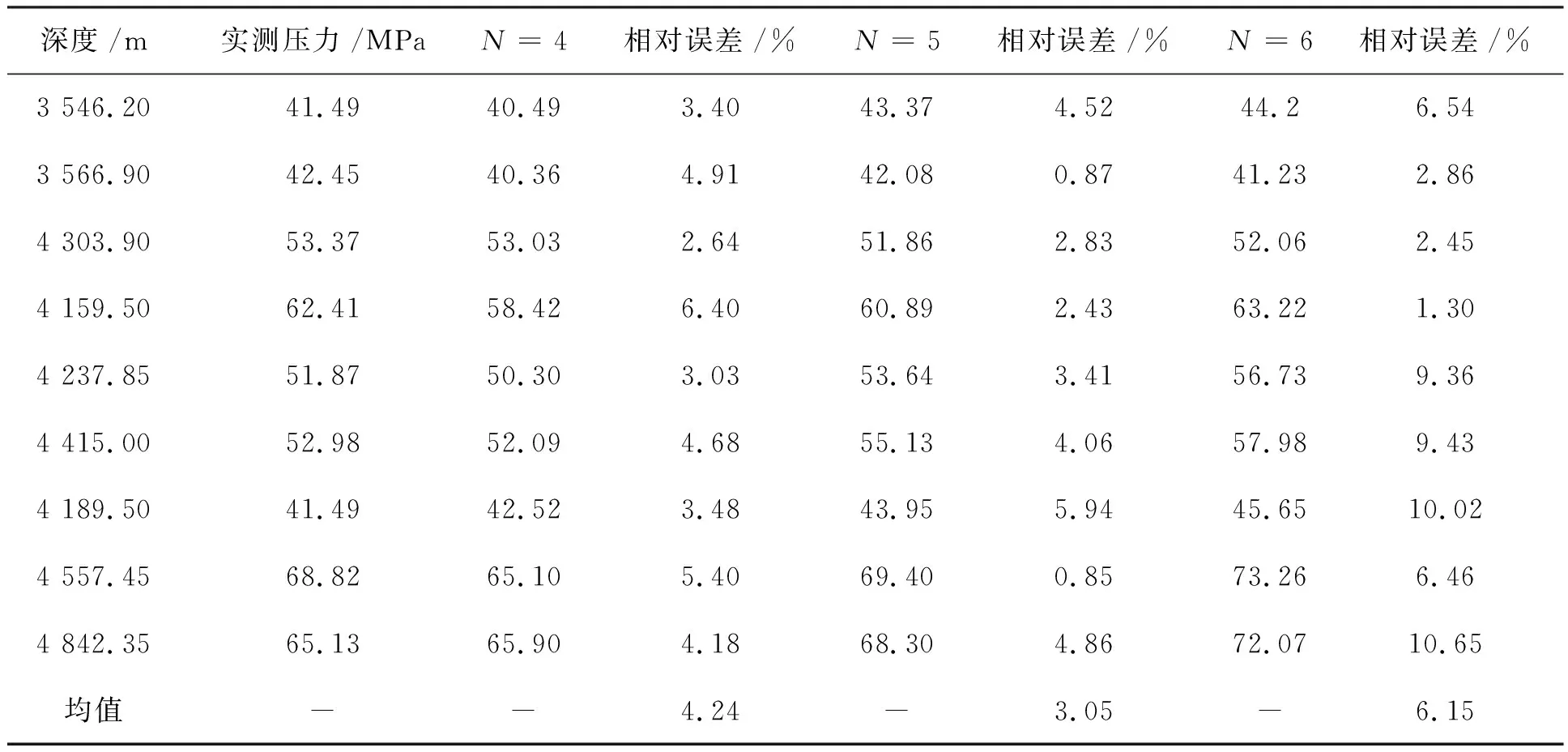
表3 西斜坡伊顿指数选取表(共5口井)

从表3得出：在西斜坡伊顿指数区N=5时，采用Eaton法预测误差可以达到最小值，精度最高.

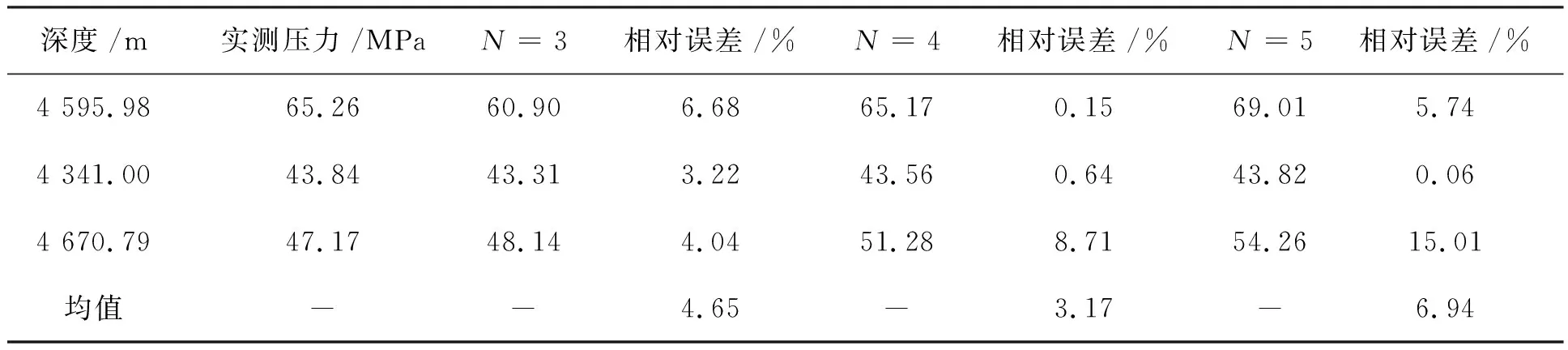
表4 西次凹伊顿指数选取表

从表4得出：在西次凹用Eaton法进行压力预测时，当伊顿指数选取N=4时，误差最小，精度最高.

表5 中央反转构造带伊顿指数选取表

从表5的Eaton指数选取和误差分析可以看出：在中央反转构造带当Eaton指数N=5时，误差最小，精度最高.

3 Bowers法

通过实验研究和理论分析发现，泥岩的原始压实曲线可以用下式描述[5]:

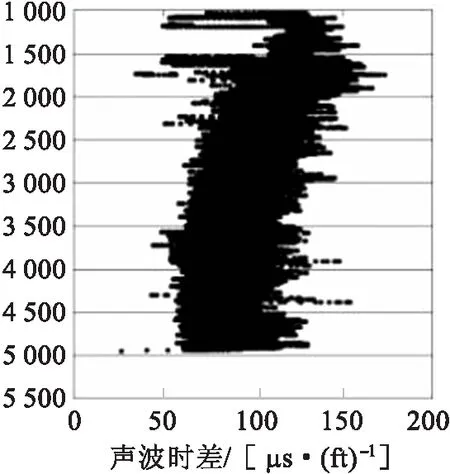
图2 西斜坡声波时差与深度关系图

V=5 000+AσevB

式中：v是声波速度，σev是垂直有效应力；A和B为系数，由临井(V,σev)数据(σ由实测地层压力或正常压实段数据获得)回归求得.

卸载曲线可用如下方程表示：

式中，σmax由下式确定:

据图2、图3井1其卸载点深度为3 450 m，Vmax为3 912.658 m/s.

据图4可得Bowers法A、B系数分别为98.12、0.865，且泥岩弹塑性系数U取5最为合适.

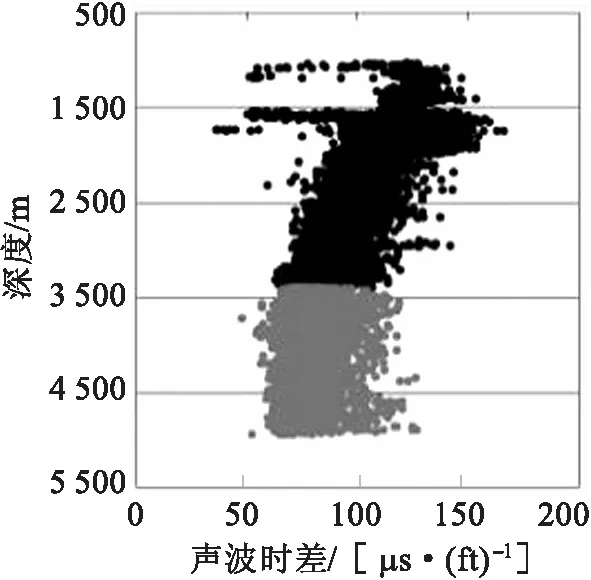
图3 西斜坡声波时差均值与深度关系图

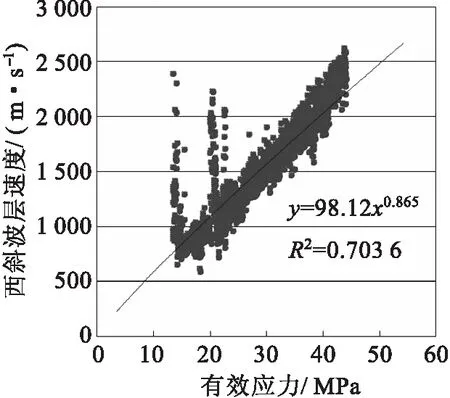
图4 有效应力与层速度的关系

从表6数据可以看出：Bowers法预测方法在西湖凹陷预测中，西斜坡处预测误差可以达到2.93%，达到了预测要求.因此，利用Bowers法在西湖坳陷进行压力预测是可行的，预测误差较小，精度适合预测.[6]

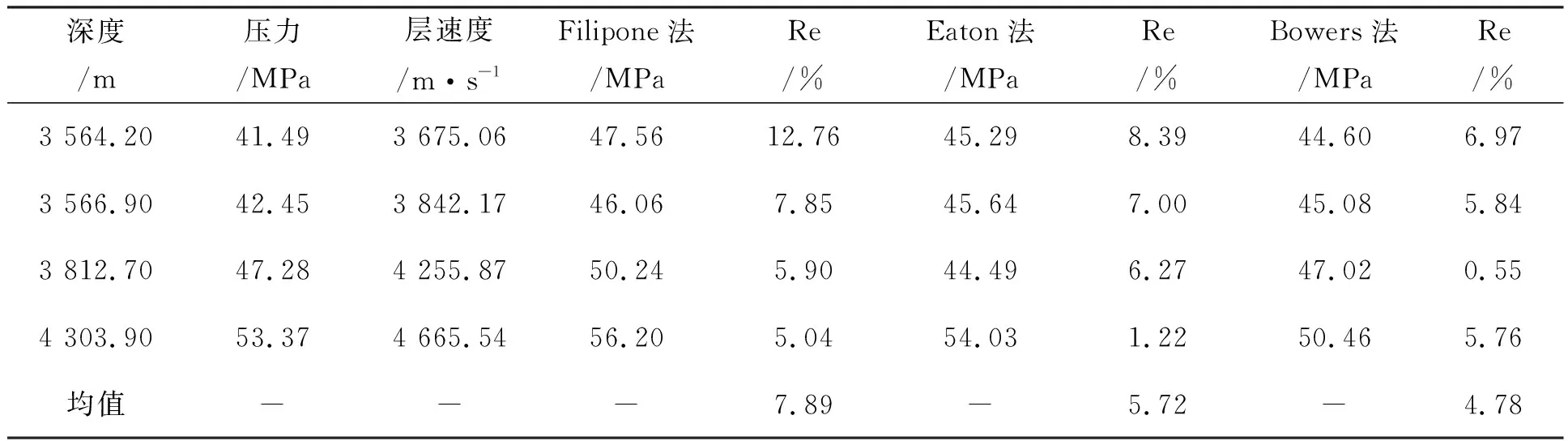
表7 井1压力测试方法对比表

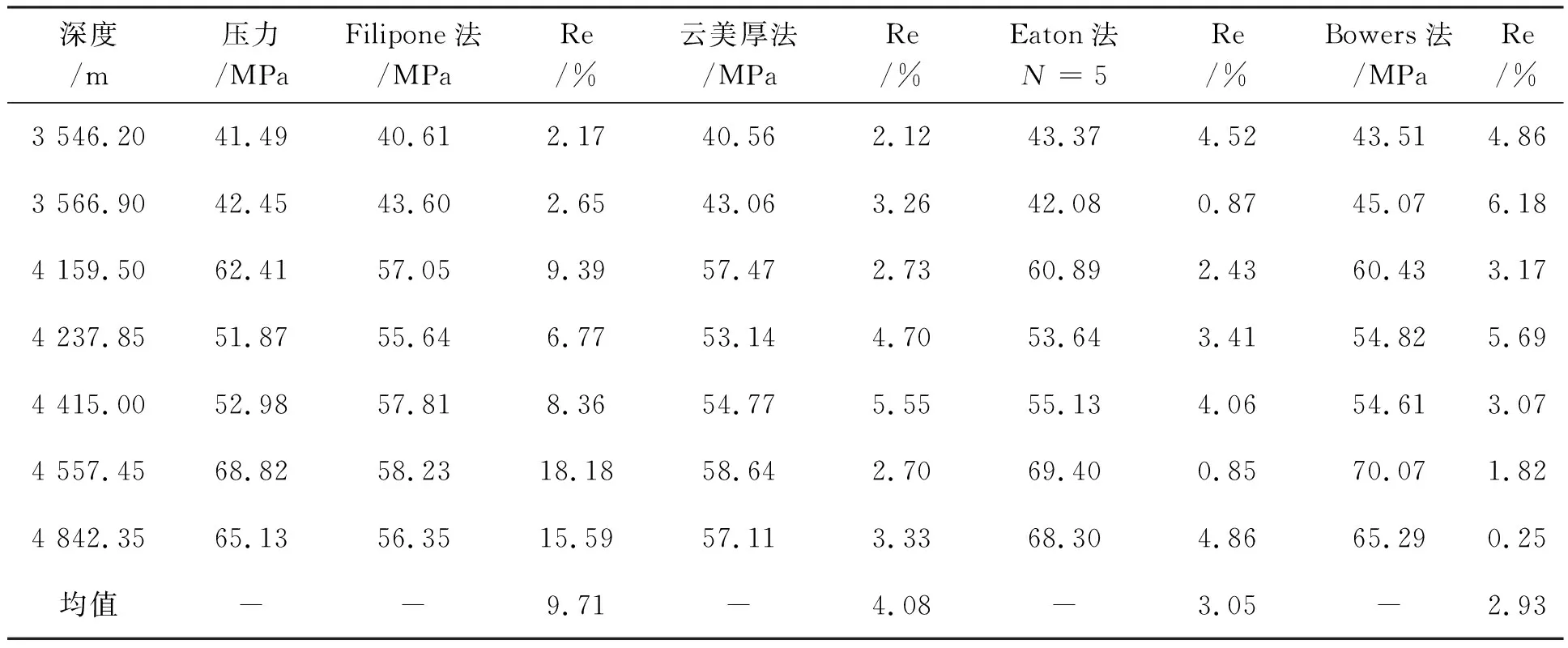
表8 西斜坡压力测试方法对比表

由表7、表8综合对比可以看到：

(1)Eaton法预测相比Fillippone法预测效果较好.究其原因，从方法原理即可看出，Fillippone法完全是速度的运算，骨架速度、流体速度分别以最大速度和最小速度代替；仅有一个校正系数也是与速度有关(C=C0*exp(a*Vp))，而且不便与测井资料相互校验，因此比较适用于无井或井资料较少地区应用.而Eaton法所使用的正常压实趋势线、伊顿指数等都是通过井数据来确定的，地震速度资料与井资料结合，相互校验，可以得到比较高的预测精度，适合有较多井资料的地区使用.

(2)Bowers法预测相比Eaton法预测更加适合西湖凹陷的压力预测.因为已知西湖凹陷主要是以生烃增压为主，不同于压实成因的其他的凹陷.系统考虑了泥岩欠压实及欠压实以外的所有影响异常压力的因素.而Eaton法可以对欠压实以外成因的流体膨胀高压做出很好的预测.