从电子邮件记录文件侦测异常使用行为

余苏毅

(宁德师范学院 信息与机电工程学院,福建 宁德 352100)

当内联网(Intranet)与因特网连接时，最重要的即是确保内联网的安全性，避免重要的数据被串改或入侵.现今对于内联网安全的维护，主要是应用防火墙(firewall)技术，将可能危害系统安全的来源杜绝于该内联网之外.相对于防火墙以阻断来源的方式确保安全，本系统进行的方式着重于分析在一般状况下，这些数据与数据的分布范围，藉由此方式的分析，日后当系统发现网络上有类似异常群集的行为时，极有可能是非法的入侵或蓄意破坏，此时即可迅速的通知系统管理员，以便做出必要的处置.

1 电子邮件记录文件数据分析

本论文以校园网络“电子邮件系统记录文件”数据作为数据挖采实验的对象，以下数据为交通大学计算机中心，信件服务器所撷取的信件收发记录文件[1]，源文件内容如表1所示.

表1 原始信件服务器记录文件数据

经过整理分析，我们可大致将log所提供的信息，整理如下：

寄件时间: Nov/3/05:20:21

机器名称: ccse

程序名称[process编号]: sendmail[26621]

队列编号: FAA26621

来源: from=DBT@gmail.gcn.net.tw

信件大小: size=382

处理等级: class=0

寄件优先权: pri=30382

收信者数量: nrcpts=1

讯息编码: msgid=<1997…>

发件人身份信息: ctrladdr=root(0/1)

经过资料的定性分析，除了过滤掉不适合的log参数，针对我们统计过后的资料加以评断，欲判别特定来源主机(或账号)是否属于异常使用状况[2].主要依下列原则判断：

(1)信件的大小.(2)发出时间是否非常集中.(3)信件来源，寄信对象有特定或异常.(4)信件传递路径.

表2的数据为从系统记录统计过后数据，藉由专家的经验，针对不同来源位置，筛选并计算系统记录文件发信笔数、信件大小、间隔时间.

将表2的判别数据，用统计图表画出，结果如图1.藉由气泡图来表达3个dimension的概念，X轴表示同一主机的发信数量，Y轴表示该主机的异常程度，而气泡的大小则表示该主机的平均发信大小.[3]

2 针对电子邮件，作异常行为侦测

2.1 一般分群算法的分析

观察传统分群算法，可以发现，一般的分群算法并不适合用于找寻大量数据中异常群集，原因有以下两点：

(1)异常行为数据在所有的log数据中，所占的比例非常的小，且各项参数数值与其它正常数据差异极大，在一般的分群算法中，常视此种数据为错误数据(noise)，不是忽略不计，就是给予较低的权重值，以避免影响其它数据的分群.

但是相反地，我们在此log数据分群的目标，便是想要凸显极少数，极特异的异常数据，因此反而应给予较小的、异常的noise资料，较高的权重.

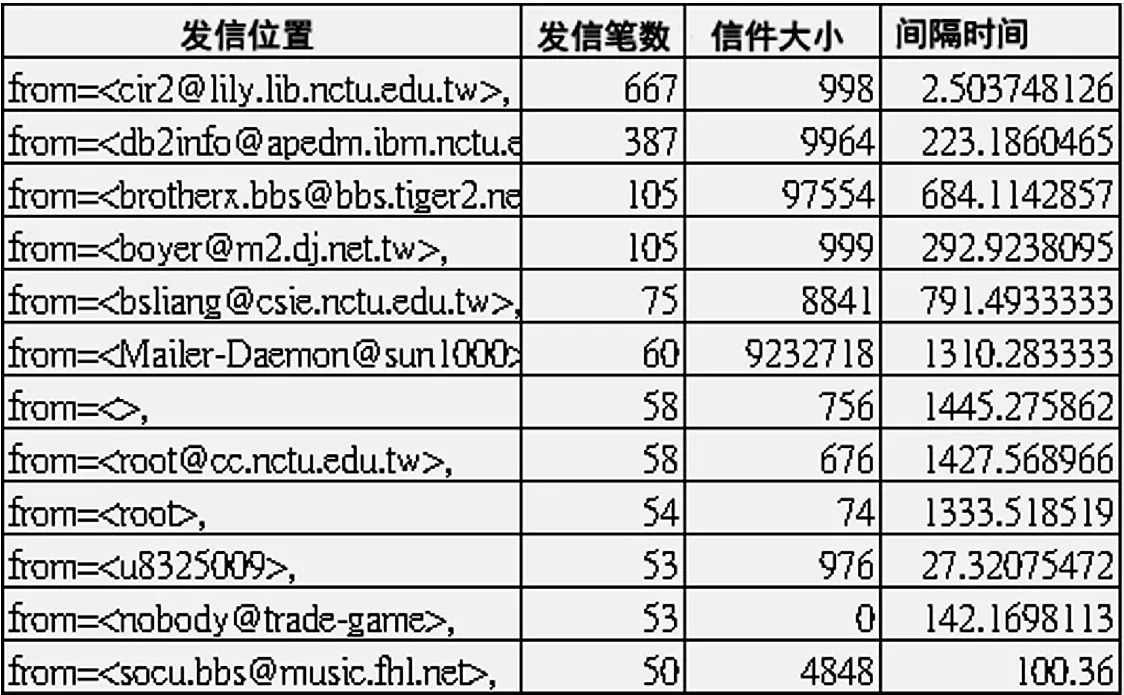
表2 经由专家判别过后的数据

图1 专家判定后的异常程度统计图

(2)在一般的分群法需O(n2)的时间花费，但log数据动辄数万笔，非一般数十笔的实验资料可以比拟，因此必须找寻一个在合理时间内，可以概略分群的快速算法.

基于以上原因，我们将使用一个改良式的K-means分群算法[4]，将大量数据作粗略的概分，并允许所分的群数大于原先所定的目标群数k，以确保noise的群集也可以被K-means算法视作独立的群集.接着将k个群重心建构成一个“最小展开树”(minimum spanning tree)，依据联机的距离，截断k-1条较长的联机，所剩的k个群集便是我们希望求得的k群.

2.2 改良式K-means算法

在传统K-means(by Forgy in 1965)算法中，会因为不同的起始点而造成不同的结果.且在数据量极大的情况下，并不适合做不同起始点的比较.[5]举例来说，若有50笔的数据欲分为五群，则所有的情况就会有7.4×1 032种(Kaufman and Rousseeuw,1990).因此，我们采用一个“跳跃式”的启发策略(heuristic)[6]，来帮助我们将较外围或较异常的数据独立出来.

与传统算法相同，我们在初始状态定义欲分群数据M={x1,x2,…,xm}，xi属于Rn及任取k个起始中心C={z1,z2…,zk}，然后逐一将每笔数据归入与之最接近的群集.在将一笔数据加入群集时，我们同时除了更新该群集的中心点外，并计算出所有群集间的最小距离min(C).故在将数据归入群集前，比较数据与群集的最小距离min(d)与min(C).若min(d)大于min(C)，则将该资料独立成新的群中心[7].如此，当距离较远的异常数据都会因此被独立出来而自成一群.δ为每次递回时的最新群数.

min(C)=min‖zj-zh‖2fori,h=1,2,…,δ，j≠h

min(d)=min‖xi-zj‖2fori=1,2,…,m，j=1,2,…,δ

但是，在最差的情况下，会因上述的分割策略，导致每笔数据皆自成一群.因此,为了避免这种情况，我们需定一个分割的上限值kmax.若分割的群数超过kmax时，便合并群集中距离最短的两群.

在此,我们要特别说明，本论文所使用的分割策略极类似ISODATA算法(Tou and Gonzalez,1974)[8]，不过此算法所提的分割与合并策略，不像ISODATA是在初始状态即限定分割或合并的参数值：若一群中数量太多即分割，若两群太近即合并.改良算法中的合并，分割操作，是完全依照当时分群的需要而定，唯有分割上限值，才需由专家视数据的多寡与特性后设定.

在第一阶段的改良K-means后，若所分的群数为δ.在第二阶段中，我们使用“最小展开树”来作合并的动作.因为K-means算法是以“平方差总和”(sum of square-error)作为评断分群结果的好坏，然而此法无法用于凸显异常的群集.因此，我们采用图形分群理论中的最小展开树.将δ群的群中心视为节点，利用Prim’s MST算法，建构成一最小展开树.依照愈是离群所居的群集愈是异常的概念，截断前k-1条最长的联机，所得的k群，便是我们所欲求的分群结果.

3 实验结果与分析

(1)首先我们先以Iris data 为实验数据，与传统K-means算法作比较,结果如图2所示.

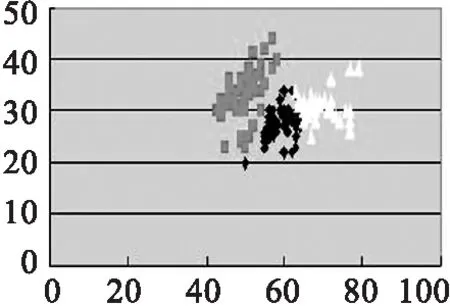
(a) 传统K-means，k=3

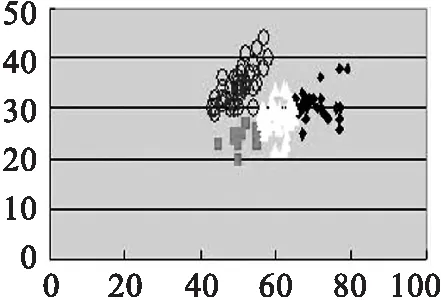
(b) 传统K-means，k=4

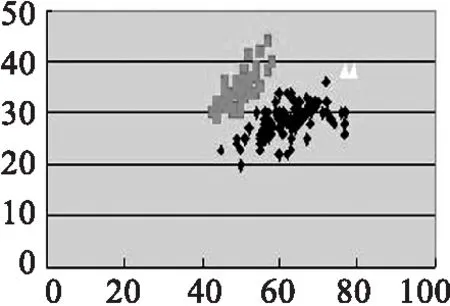
(c) 改良K-means，k=3

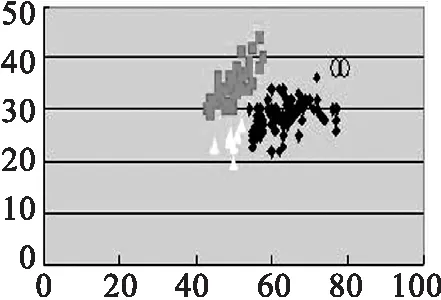
(d) 改良K-means，k=4

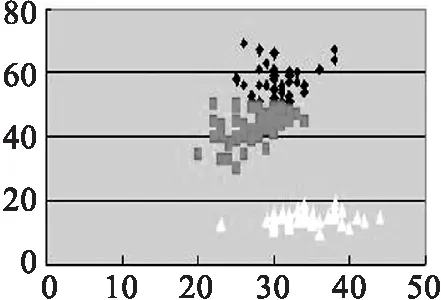
(e) 传统K-means，k=3

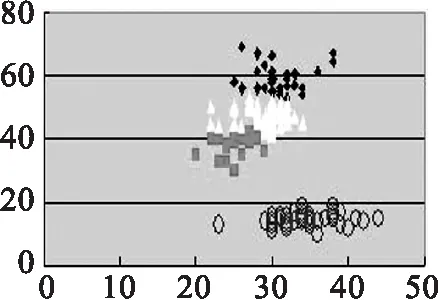
(f) 传统K-means，k=4

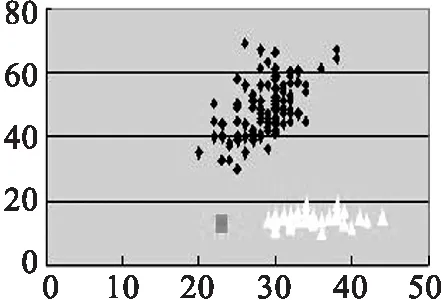
(g) 改良K-means，k=3

(h) 改良K-means，k=4

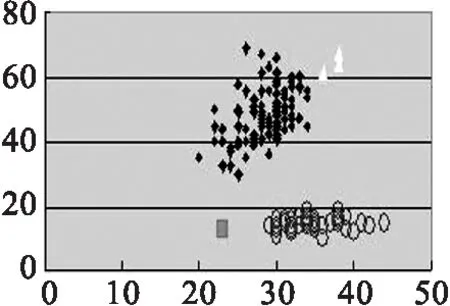
(a)(b)(c)(d)的实验数据源为取Iris第1,2个参数值.(e)(f)(g)(h)的实验数据源为取Iris第2,3个参数值.

(2)我们再以log data为实验数据，与传统K-means算法作比较

实验数据为25 511笔，欲分为六群，为了容易观察，我们取二个参数值：发信的数量(X轴)，信件的大小(Y轴).分群的结果如图3所示：

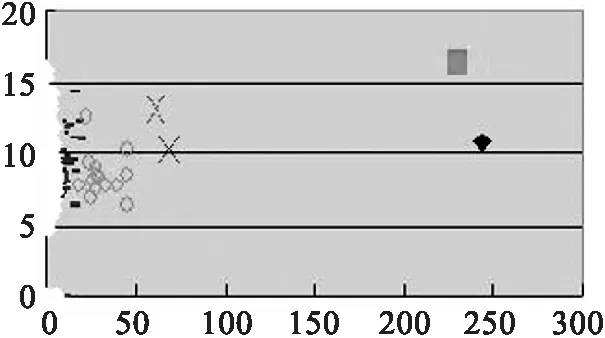
(a) 传统K-means，k=6

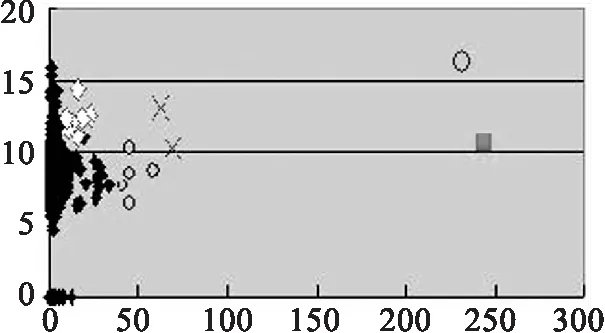
(b) 改良K-means，k=6

由实验结果的图示，我们可以观察到凡是使用传统K-means算法的分群结果大抵皆会将一个大的群集分割为数个小群集，以降低分群的总平方差(sum of square-error)[9].而藉由改良式算法所得的结果，因为经过最小展开树依距离的远近重新分群，所以会将较远的异常群集独立出来.经由以上的分群作业，可以将邮寄记录中的异常行为来源者，清晰地过滤出来，可作为系统管理者在管理或决策上的辅助.

4 结论与未来工作

在一般的分群算法中，即使异常群集在起始时设定为起始中心，但常因数量不多或距离不够远，最后被并入另外的群集中，而无法突显出来.藉由本文所提的两阶段式分群法，在第一阶段里使用改良式K-means算法，适合用于大量数据，快速地将群集的资料分隔出来.再配合跳跃式的分割特点，使得外围或较小群集也可以被区隔出来.在第二阶段中，使用最小展开树的节点远近关系，作为判断该群集是否较为异常的指标.由实验结果可知，改良后的算法用于找寻异常群集要比传统的分群算法来得好.

目前为止，我们已经对电子邮件数据作详尽的分析与提出一个可筛选异常数据的算法，此法可适用于其它在大量数据中过滤异常的群集数据.然而，在实际的网络管理工作上，仍然有许多管理上的漏洞，有待我们进一步努力，研究更有效的侦测工具，去侦测和防范网络使用中的异常行为.