正弯矩作用下平齐端板连接钢管混凝土节点的承载力计算
王冬花, 亓 萌,2
(1.安徽工商职业学院 会计学院,合肥 231131; 2.合肥工业大学 土木与水利工程学院,合肥 230009)
钢结构、组合结构在地震中所发生的危害超出了人们的预期,从1994年美国Northridge地震、1995年日本Kobe地震和1999年台湾集集地震都可以得到这样的结论,地震中此类结构中的节点都出现了严重断裂损伤[1],给社会造成了大量的经济损失和人员伤害.
钢管混凝土组合节点是端板连接钢管混凝土组合节点,该节点是钢-混凝土组合梁与钢管混凝土柱通过端板和单边高强螺栓连接而成,主要有平齐端板连接和外伸端板连接两种类型.节点区楼板内设置抗剪栓钉和连续贯穿钢筋来保证节点的组合作用.试验研究表明[2],此类组合节点具有良好的半刚性,其施工快捷方便、受力性能和抗震性能好,且造价较低.
近年来,国内外学者对H型钢柱与钢-混凝土组合梁平齐端板连接节点进行了大量的试验研究,并提出了负弯矩作用下此类节点的抗弯承载力简化计算方法[3-6].针对正弯矩作用下平齐端板连接钢管混凝土组合节点的可能失效模式,提出对称荷载和非对称荷载作用下组合节点的力学模型和各组件承载力简化计算方法,给出了正弯矩作用下平齐端板连接组合节点的抗弯承载力计算公式,并通过试验结果进行了验证.
1 正弯矩作用下组合节点的抗弯承载力
1.1 计算假定
在地震作用下,混凝土楼板的受力相对较为复杂,此时组合节点会受到正、负弯矩的交替作用,在正弯矩作用下,混凝土楼板一般都是位于受压区,压力由柱壁和混凝土楼板相接触的局部受压面承担,拉力则由节点区下部高强螺栓承担.节点破坏形式通常是受压区内的混凝土楼板压碎、端板发生受弯破坏、连接区域下部受拉螺栓破坏等.
为了得到平齐端板连接组合节点抗弯承载力计算公式,充分考虑受压区混凝土楼板在受力过程中的抗压作用,本文做了如下计算假定:
①不考虑螺栓、楼板内纵向受力钢筋的抗压作用;
②不考虑钢梁的受拉,钢梁受压区内均达到其材料屈服强度,且应力分布均匀;
③不考虑楼板钢筋与柱锚固失效;
④不考虑平齐端板与钢梁连接处焊缝破坏;
⑤混凝土楼板与钢梁之间抗剪栓钉连接可靠有效,钢管混凝土组合梁抗剪承载力可以充分发挥;
⑥受压区内混凝土楼板的有效计算宽度取钢管混凝土柱的宽度D(对于圆钢管混凝土柱,取钢管外直径D);
⑦受压区内混凝土楼板的压应力达到混凝土抗压强度且分布均匀.
1.2 平齐端板连接钢管混凝土组合节点的抗弯承载力计算
为了得到正弯矩作用下该组合节点的抗弯承载力计算公式,假设有n排单边螺栓连接此组合节点,根据五种不同的塑性中和轴的位置进行了以下划分.
第一种情况(见图1):组合节点受拉区为第一排至第m-1排螺栓,受压区第m排螺栓以上.
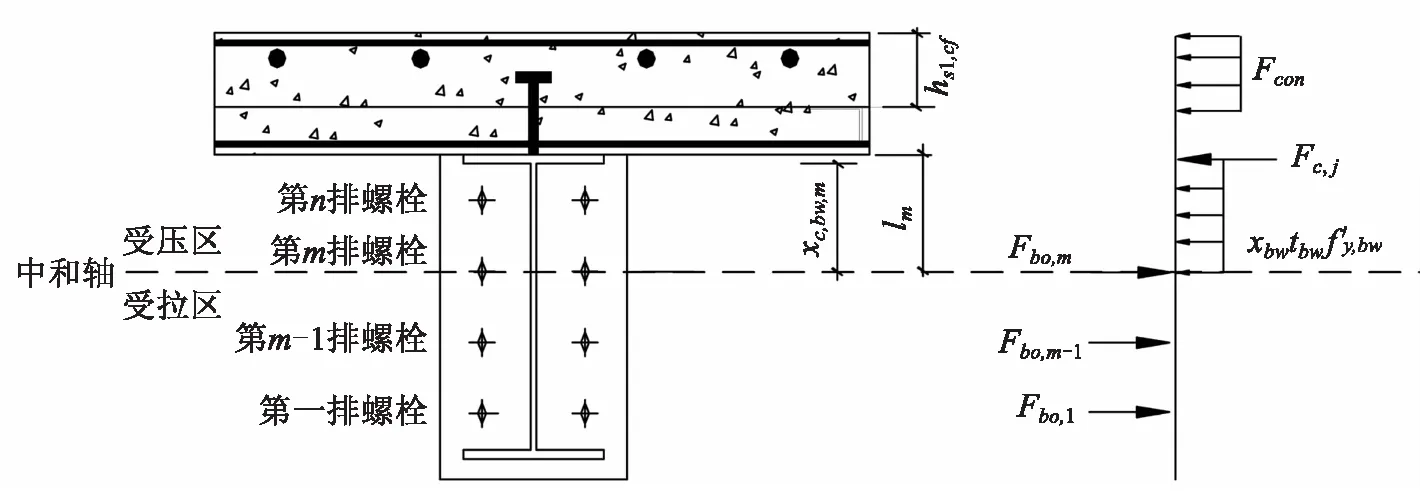
图1 第一种中和轴位置
在此情况下,第m排螺栓上方为塑形中和轴位置,组合节点各组件的受力应满足下式:
(1)
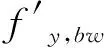
(2)
式中:fy,bw为H型钢梁腹板的屈服强度,τxy为H型钢梁腹板内的剪应力,按下式计算:
τxy=V/(hbw·tbw)
(3)
式中:V为作用在连接处剪力,hbw为H型梁腹板的高度.
Fcon为混凝土楼板与柱翼缘接触处的局部抗压承载力,按下式计算.
Fcon=0.67β·bcf·hsl,cf·fcu
(4)
式中:fcu为钢管柱混凝土立方体抗压强度;hsl,cf为钢管混凝土柱与混凝土楼板相接触处的厚度,bcf为钢管柱截面宽度,β为混凝土局部受压强度的增大系数,建议取1.25.
H型钢梁腹板受压区边到腹板上翼缘的距离即实际相对受压区高度为:
(5)
式中:pb为第一排单边高强螺栓到组合梁下翼缘上表面的距离,hb为H型钢梁截面高度,p为螺栓各排的间距.在此情况,受压的是1~m排螺栓,第m排螺栓的抗拉承载力Fbo,m应按下式计算:
(6)
正弯矩作用下此组合节点的抗弯承载力为:
(7)
式中:li为第i排螺栓中心至混凝土楼板与组合梁翼缘相接触的距离,i=1,2…,n.
第二种情况(见图2):第一排至第m排螺栓全部受拉.
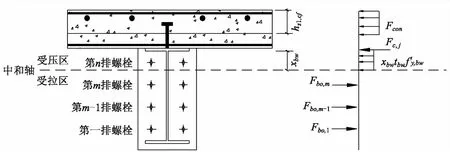
图2 第二种中和轴位置
此种情况实际中较为常见,受拉区为第一排至第m排螺栓,受压区为混凝土楼板,第m排螺栓上方为完全中和轴位置,受力平衡方程为:
(8)
根据平衡条件,钢梁腹板的受压区高度为:
(9)
此时对H型钢梁上方的受压混凝土楼板中心求矩,则此组合节点的抗弯承载力:
(10)
第三种情况(见图3):所有单边高强螺栓都受拉,H型钢梁上翼缘下方为中和轴位置.
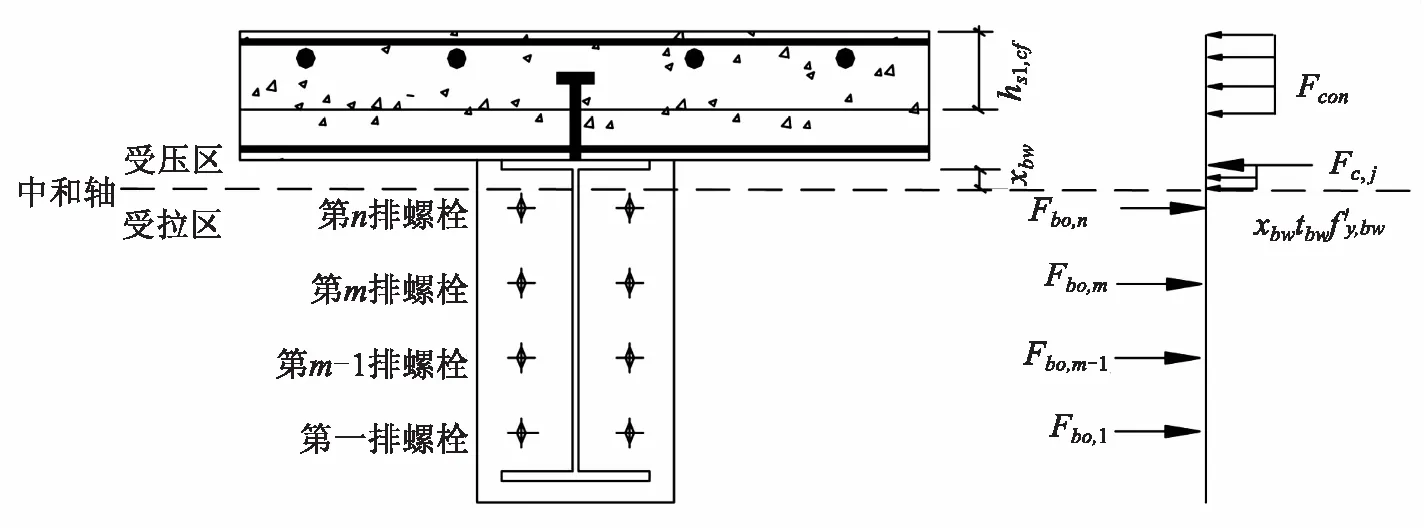
图3 第三种中和轴位置
在此情况下,受力平衡方程为:
(11)
根据平衡条件,钢梁腹板的受压区高度为:
(12)
式中:pt为第n排螺栓至钢梁上翼缘下表面的距离.
此时,对钢管柱翼缘与混凝土楼板接触处厚度中心求矩,则此组合节点的抗弯承载力为:
(13)
第四种情况(见图4):中和轴位于钢梁上翼缘.
在实际情况中很少出现,在螺栓的极限抗拉承载力较或低配置螺栓数目不足时才会出现.
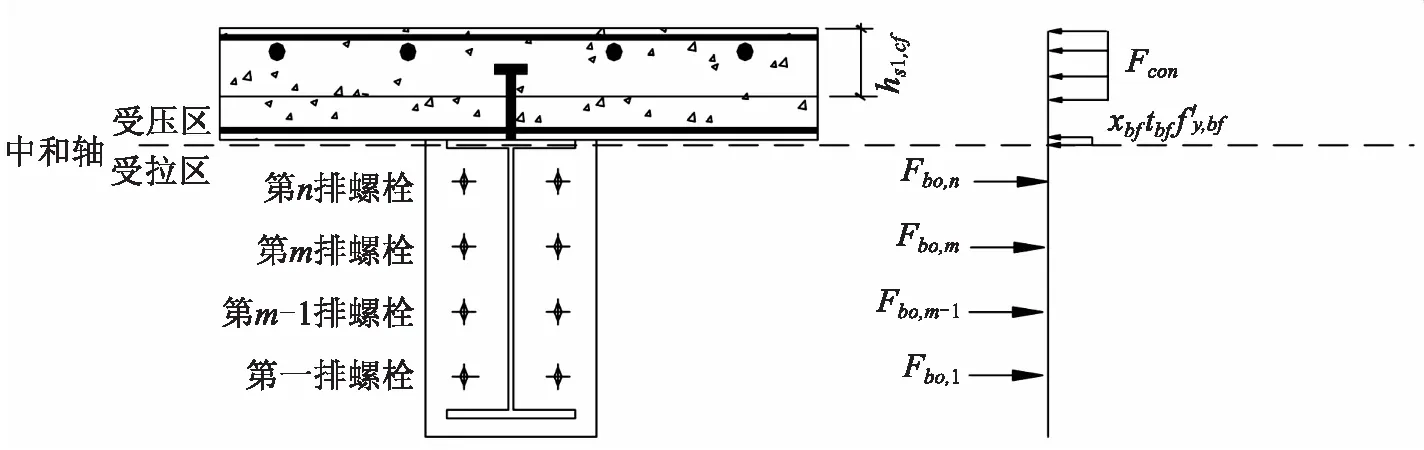
图4 第四种中和轴位置
此时所有螺栓均位于受拉区,受力平衡方程为:
(14)
式中:fy,bf为H型梁翼缘屈服强度,bbf为H型钢梁翼缘宽度.
则钢梁上翼缘的受压区高度为:
(15)
钢梁上翼缘所承受压力Fc,bf按下式确定:
(16)
此时,对钢管柱翼缘与混凝土楼板接触处厚度中心求矩,则此组合节点的抗弯承载力为:
(17)
第五种情况(见图5):中和轴位于钢梁上翼缘的混凝土楼板内.
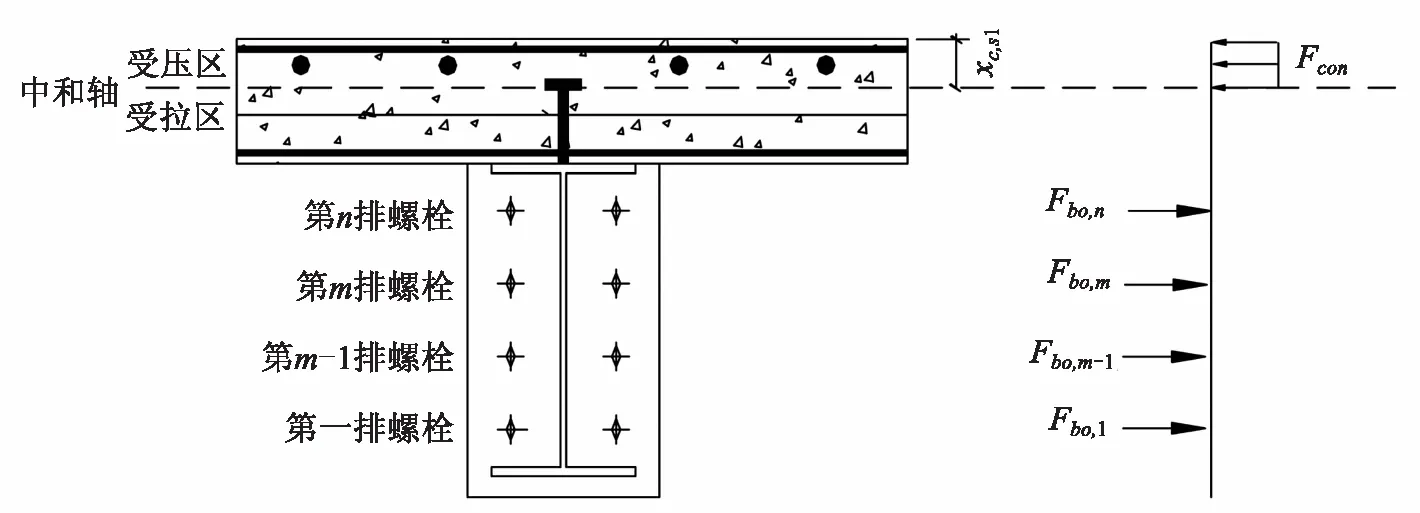
图5 第五种中和轴位置
这种情况一般出现在螺栓的极限抗拉承载力非常低或配置螺栓数目严重不足时,此类情况较为少见.
此时所有螺栓均位于受拉区,处于受拉状态,受力平衡方程为:
(18)
则混凝土楼板内的受压区高度xc,sl为
(19)
此时,对钢管柱翼缘与混凝土楼板接触处厚度中心求矩,则此组合节点的抗弯承载力为:
(20)
2 试验验证
本文对比了平齐端板连接钢管混凝土组合节点在正弯矩作用下抗弯承载力计算公式和2榀带楼板平齐端板连接钢管混凝土组合节点试验[7]结果.试件的详细尺寸信息见图6和表1.试验采用10.9级M20单边螺栓,单边螺栓性能及其构造见文献[7].试件具体安装见文献[2].试验程序采用美国ATC-24加载制度.主要量测了组合节点侧向位移、柱水平位移、柱端水平荷载,核心节点区楼板内纵向钢筋、H型钢梁、端板和钢管的应力分布.
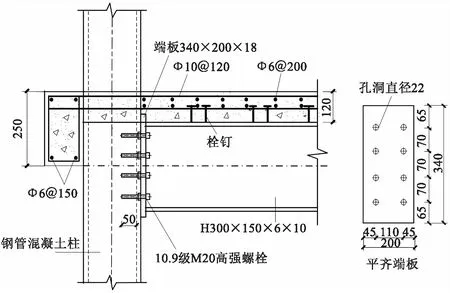
图6 试件尺寸详图

表1 试件尺寸一览表(mm)
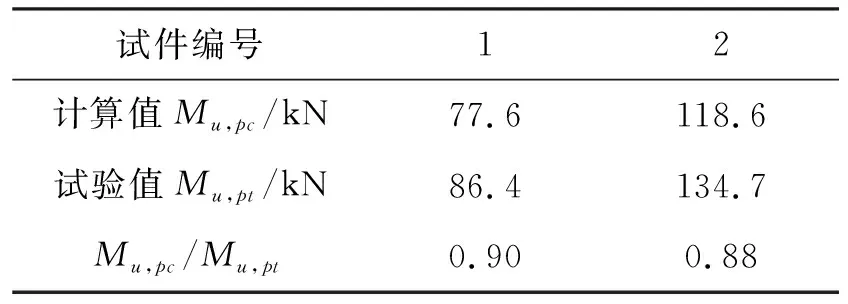
表2 试验结果与计算结果比较
3 结论
本文基于力学平衡原理,利用塑性分析方法,考虑不同塑性中和轴位置,获得了在正弯矩作用下此类组合节点的承载力计算方法,并将其与试验结果进行了比较(见表2).从比较的结果可以看出,本文所提的简化计算方法具有一定的准确性,在平齐端板连接的钢管混凝土组合框架设计中可以应用此公式.

