关注数学思想 培养数学素养—以低年级数学教学为例

任季芳

（福建省福州市马尾区教师进修学校，福建福州 350015）

引 言

我国学生数学学习培养，历经了由六大核心素养（数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析），到《全日制义务教育数学课程标准（2011年版）》明确提出的10个核心素养（数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识）。这些核心素养是数学思想、数学方法或者关于数学的整体理解与把握，是学生数学素养的表现，其中最基本的核心素养有三个，即数学抽象、逻辑推理、数学建模。下面以低年级数学《1000以内数的认识》《排队中的学问》教学为例，谈谈三个最基本的核心素养的培养。

一、数学抽象，让学生的思维“动”起来

数学是一门抽象性、逻辑性很强的学科，数学知识的探究过程实质上也是数学抽象思想的感悟过程。教学中，教师要将抽象思想融入学生具体的数学学习过程中，让学生在解决数学问题的过程中，逐步领悟抽象思想在数学中的运用[1]。

例如，教学二年级数学《1000以内数的认识》这一课时，为了让学生感知1000的数量，让学生4人一组，准确数出100粒红豆装入小袋子（见图1），再让10个小组代表将各组小袋子装的100粒红豆陆续倒入透明杯中，并进行实时投屏。学生们一边看着一边认真地数着：1个百、2个百、3个百……9个百（见图2），此时教师强调：再添上1个百是几个百？学生回答：10个百，教师接着问：10个一百是多少呢？师生共同得出：10个一百是一千，从而让学生们感知1000粒红豆的数量。

图1 数红豆

图2 学生将红豆倒入透明杯中

又如，教学一年级数学《排队中的学问》一课时，让学生们求：小丽和小宇之间有多少人（见图3）？

图3 小丽和小宇之间有多少人

有的学生喜欢用“数一数”的方法，而有的学生则喜欢用“画一画”的方法，教师给予学生们充分的时间交流合作，学生们将抽象的数量关系用不同的符号来表示，如□、△、○、☆等（见图4）。

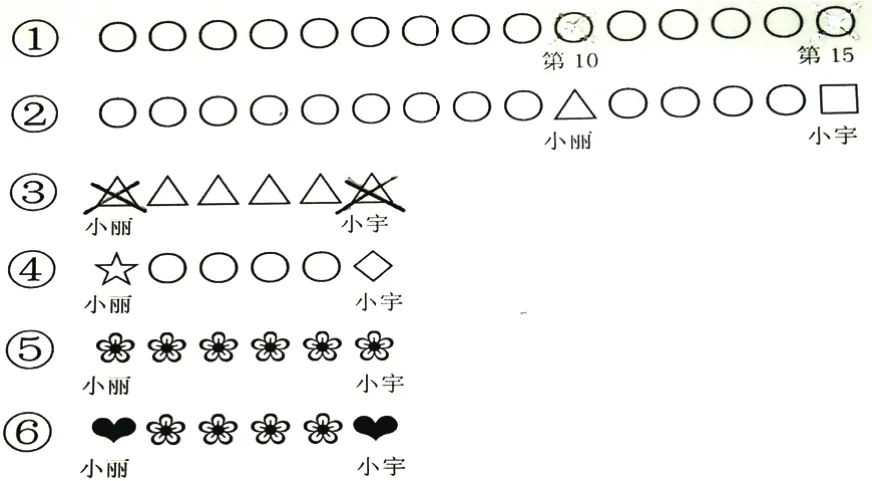
图4 用不同符号表示抽象的数量关系

把抽象的数量关系转化为学生容易理解的图形，这一过程渗透着符号化思想，既降低了解题难度，又体现了多样化的教学策略。符号化过程其实也是抽象过程，抽象思想与符号化思想如影随形。抽象思想存在于数学学习的全过程，虽然低年级的数学知识看起来简单，但实际上也充满了抽象，教师要从低年级教学开始就关注抽象思想的渗透，培养学生数学素养。

二、逻辑推理，让学生的思维“活”起来

推理是从一个或几个已有的判断得出另一个新判断的思维形式。《义务教育数学课程标准(2011年版)》明确指出“推理能力的发展应贯穿在整个数学学习过程中。推理是数学的基本思维方式，也是人们在学习和生活中经常使用的思维方式……”。在利用数学解决各种实际问题的过程中，虽然大量的计算可以通过计算机来完成，但是就培养人的思维能力而言，推理能力仍然是至关重要的，因而推理能力必然是小学生数学素养的重要内容之一，教师要从低年级起就开始注重培养学生的这种能力。

例如，《1000以内数的认识》一课中有这样的练习题练习找规律数数：

学生通过观察发现，不仅可以100个100个地数、10个10个地数、1个1个地数，还可以从大到小数、从小到大数，因而得出六种结果：

发现规律的过程，也是推理的过程。在这过程中，学生又惊讶地发现此题还可以2个2个、5个5个、30个30个……地数，可以有无数种有规律的数法。在这一过程中教师尽量让学生用语言说出自己的发现，从而使其数学思维得以丰富、提升。教师有意识地引领学生感悟推理的过程，经过长时间累积，逻辑推理就会慢慢内化成学生自己的数学素养。

在教学中渗透数学基本思想要经历一个循环往复、螺旋上升的过程，而且常常是好几种思想交织在一起，因此教师要从低年级开始，把抽象的数学思想逐渐揉进具体的数学知识内容中。

三、数学建模，让学生的思维“亮”起来

数学模型是用数学语言概括地或近似地描述现实世界事物的特征、数量关系和空间形式的一种数学结构。数学的概念、定理、规律、法则、公式、性质、数量关系式等都是数学模型[2]。在小数教材中，模型无处不在，学生学习数学知识的过程，实际上就是对一系列数学模型的理解、把握的过程。

例如，教学《1000以内数的认识》拐弯数数时，借助算盘：（1）1个1个地数，从335数到342，数到339时，个位上9，添上1个珠子即10个1，个位上退去10个珠子，向十位进1个珠子，即340；（2）10个10个地数，从460数到530，数到490时，十位上9，添上1个珠子即10个10，十位上退去10个珠子，向百位进1个珠子，即500；（3）100个100个地数，从700数到1000，数到900时，百位上9，添上1个珠子即10个100，百位上退去10个珠子，向千位进1个珠子，即1000。在拐弯数数过程中建立模型：无论哪位满十，都向前一位进1。利用建立的数学模型，让学生拨珠练习“999添上1”，即个位9添上1满10向十位进1，十位9添上1满10向百位1，百位9添上1满10向千位1，得出999后一个数是1000。数数中学生能熟练掌握并运用满10进1的十进制原理，反映着模型思想在数学中的应用。

又如，教学《排队中的学问》中的练习题，求“小丽和小宇之间有多少人？”（见图5）

图5 以画圈的形式表示小丽和小宇之间有多少人

有的学生发现“求小丽和小宇之间有多少人？”还可用“算一算”的方法：“15-10-1＝4（人）”。在学生说明每一步算式所表示的意义后，教师配合学生将静态画面动态化，帮助学生理解算式的含义，如“15”表示到小宇为止有15人（课件闪动图形总数15）；“-10”表示先减去到小丽为止的10人（课件闪动图形表示10人部分）；“再-1”表示减去小宇这1个人（课件闪动图形表示小宇1人部分），就得出小丽和小宇之间有4人。再通过“有20个同学排队买票，小西排第10，小林排第18，它们之间有几人？”的练习，让学生发现“求两数之间有多少”可以用“大数-小数-1”的计算方法得出。利用数学模型，“求两数之间有多少”尤其两数较大或中间的数较多时，“算一算”的方法更简便。

模型思想是问题解决的重要形式，是培养学生“用”数学的重要途径，有利于培养学生的创造能力。教师要从低年级教学开始就注重渗透模型思想，培养学生的数学素养。

结 语

数学思想方法正如杜甫的诗句：“好雨知时节，当春乃发生。随风潜入夜，润物细无声”。希望数学思想就像春雨一样不断滋润学生的心田，教师要从低年级开始，让数学思想方法在学生心中“生根发芽”，并为后续的学习打下基础，从而实现数学素养的提高。