基于CS和随机声呐阵列的水下目标方位估计

张红梅, 陈明杰, 刘洪丹, 孙希威



基于CS和随机声呐阵列的水下目标方位估计

张红梅, 陈明杰, 刘洪丹, 孙希威

(哈尔滨工程大学 自动化学院, 黑龙江 哈尔滨, 150001)

针对线性被动声呐的水下目标方位估计问题, 考虑到水下目标的方位相对于所有可能的探测方位是稀疏的这一事实, 采用压缩感知(CS)技术设计目标的方位估计方法。依据CS理论中的互不一致性(MIP)条件, 构造了一种阵元稀疏且随机分布的线列阵声呐结构。对以上设计的方位估计方法和声呐阵列信号进行了仿真。仿真结果表明, 采用稀疏随机声呐阵列, 并结合基于CS的目标方位估计方法, 不仅能够在水下低信噪比的情况下准确分辨空间方位集中的多个目标, 而且能够在目标源信号相干的情况进行准确的方位分辨。

水下目标; 方位估计; 压缩感知; 随机声呐阵列

0 引言

近年来, 随着水下航行器的快速发展, 水下目标的方位估计问题成为声呐信号处理的主要研究内容之一, 也是阵列信号处理[1-2]在水下应用的一个研究方向, 无论在军事领域还是民用领域都有着重要的理论意义和实用价值。军事上, 通过被动声呐获取敌方水下目标的发射信号或者噪声信号, 进而获取目标的方位, 据此制定有效的规避和打击策略; 民用上, 可通过主动声呐辅助海底勘察或海洋捕捞作业。

方位估计是指通过对来自目标的信号分析, 以获取其相对于观察者方位的技术。按照目标及其信号源的个数, 分为单目标和多目标方位估计问题。由于单目标问题是多目标问题的特殊情况, 所以文中重点研究后一种情况下的方位估计问题。

对于一般的声呐来说, 水声换能器的数量是水下目标探测结果的重要保障之一。为了提高对水下目标的分辨率, 探测声呐的设计已趋向于大孔径, 这必然会产生较高的硬件成本。另外, 水声换能器的数量越多, 数据处理的成本显然也越高。实际上, 基于适当的数据处理方式, 利用少数的声呐换能器也可实现对目标的分辨[3-4]。

文中从2个方面考虑: 1) 稀疏阵元声呐阵列的设计。一方面, 可以从物理上实现, 设计少量声呐阵元结构的阵列; 另一方面, 在实际的运算中, 不必处理所有换能器的输出数据, 而是只需随机选择部分数据处理即可。2) 声呐信号处理算法的设计。对于大孔径声呐阵列, 如果阵元个数较少, 文中称之为稀疏阵列。对稀疏阵列获取的数据进行处理, 传统算法势必受Nyquist采样定理的限制而失效。为解决这个问题, 需要设计新的数据处理算法。针对1) 中所设计的稀疏阵元的阵列结构, 考虑设计基于压缩感知(compressive sensing, CS)[5-7]的目标方位估计算法, 实现对目标方位的高分辨估计。在利用巨型声呐作快速跟踪的问题中, 上述想法是值得尝试的。

1 水下目标方位估计及声呐阵列信号模型

1.1 水下目标方位估计

一般情况下, 探测设备和目标同时处于水下的声场中。方向场表现为一系列平面波, 由远场目标信号和噪声源产生。基于被动声呐的目标探测, 就是要从声呐换能器的入射信号中区分出来自目标的信号, 并通过对信号的分析, 判断出目标所在的方位。

对于空间信号的方位估计问题, 高分辨估计技术突破了传统的波束形成技术存在的瑞利限问题, 成为主流的估计方法。其中, 子空间分析法是高分辨估计中较为成熟的方法, 典型代表是Schmidt等[8]提出的多重信号分类(multiple signal classification, MUSIC)方法。虽然子空间类估计法已足够优秀, 但是对于空间方位比较靠近的低信噪比目标信号源, 或相干的信号源, 这类方法的分辨力还是相当有限的。因此, 文中将针对这2种情况尝试引进新的算法, 并相应地通过改进传统阵列的结构, 解决上述问题。

水下目标方位估计问题的一般做法是, 首先将声场中探测方向所在的二维平面均匀划分为若干个离散角度, 来表示空间中的不同方位, 如图1所示。当声呐在水下进行作业时, 声呐阵列会接收到来自方向场中不同方位上的入射信号, 因此方向场的每个离散方位上都会对应一个信号s。一般来说, 信号能量较强的方位就是潜在的目标方位。这样, 水下目标的方位估计问题就归结为如何估计信号能量较强的离散方位的问题。显然, 在其他条件不变的情况下, 方位角的估计分辨率取决于对探测平面的离散化步长。

如果将每个离散方位上的入射信号对应的能量看作一个分量, 那么所有离散方位上的信号能量就构成了一个向量, 或者说是某种意义上的“信号”。由于目标信号源的个数相对于离散方位数来说是稀疏的, 所以这个信号就是一个稀疏信号。而水下目标的方位估计问题, 实际上就是估计稀疏信号中非零元位置的问题, 或者说是对空间稀疏信号的重构[9], 这正是CS理论所解决的问题。文中就是基于以上思路, 设计了一种基于CS理论的目标方位估计方法。

1.2 声呐阵列信号数学模型

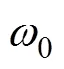
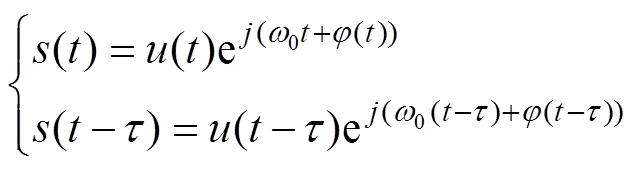
在窄带远场信号源的假设下, 有

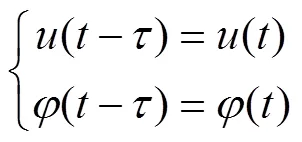
因此有

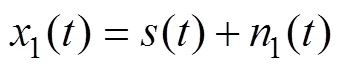
第2个阵元同时接收到的信号为

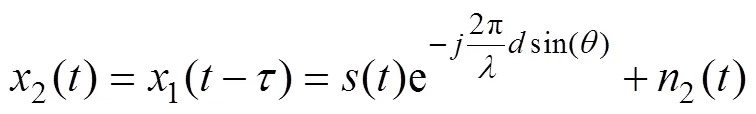
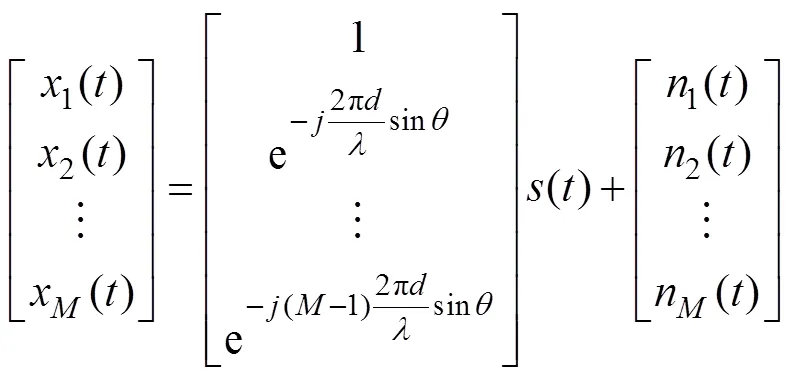
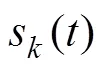
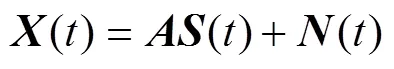
(8)

2 CS基本理论

CS是近年来出现的一种新的数据获取理论, 其最大的特点是: 完美地利用信号的稀疏特性, 可以以低于Nyquist的采样率进行采样, 并利用这些采样信号对原信号进行精确重建。

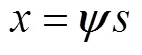
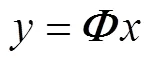
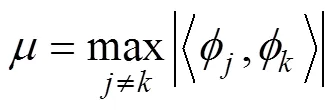
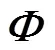
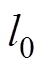
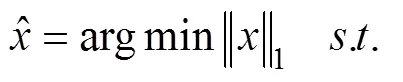
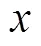
3 基于稀疏随机声呐阵列的水下目标方位估计

基于前两部分对目标方位估计理论以及CS理论的介绍和分析, 该部分将设计水下目标方位估计具体方案, 包括: 1) 非均匀声呐阵列的构造; 2) 基于CS理论的目标方位估计方法设计。

3.1 CS理论用于目标方位估计的可行性分析

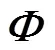
3.2 稀疏随机声呐阵列设计原理

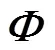
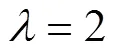
非均匀阵列的设计方法有很多, 例如按设计方法命名的最小冗余阵列、最大连续延迟阵列和最小间隙阵列是比较有代表性的3类[11]。还有利用穷举法来设计阵元间距的非均匀阵列。以上非均匀阵列设计的共同点是, 都需要利用数学中数论的知识设计阵元间距, 以使阵元位置差的集合满足一定的规律, 设计的复杂度高, 对于大型声呐阵列来说, 难度较大。

基于此, 文中对声呐阵元间距的非均匀设计采用一种容易实现且合理的方式, 即阵元间距通过随机数生成的方式产生。另外, 从整体上看, 阵元的分布还是稀疏的, 所以文中称之为稀疏随机线列阵, 以下简称随机阵列、随机阵。阵元的随机分布方式采用高斯分布。之所以选择高斯分布, 这是与基于CS理论对观测矩阵的不相关设计思想是一致的, 而且依据中心极限定理, 高斯分布是自然界最普遍存在的随机分布形式。

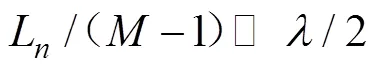
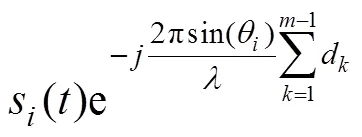
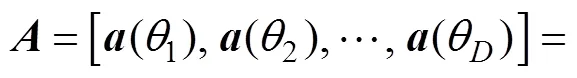
(14)

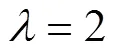
由图5可以看出, 利用稀疏随机阵列可以准确辨识3个目标的方位, 甚至是2个方位彼此非常靠近的目标源。但是采用均匀阵列时却无法分辨这2个目标。由表1中的数据可以看出, 在前2个目标附近出现了模糊角, 而方位强度最大幅值对应的方位是–27°, 与真实情况完全不同。

理论分析与仿真结果均表明, 稀疏随机线列阵对目标信号的分辨力优于均匀线列阵。

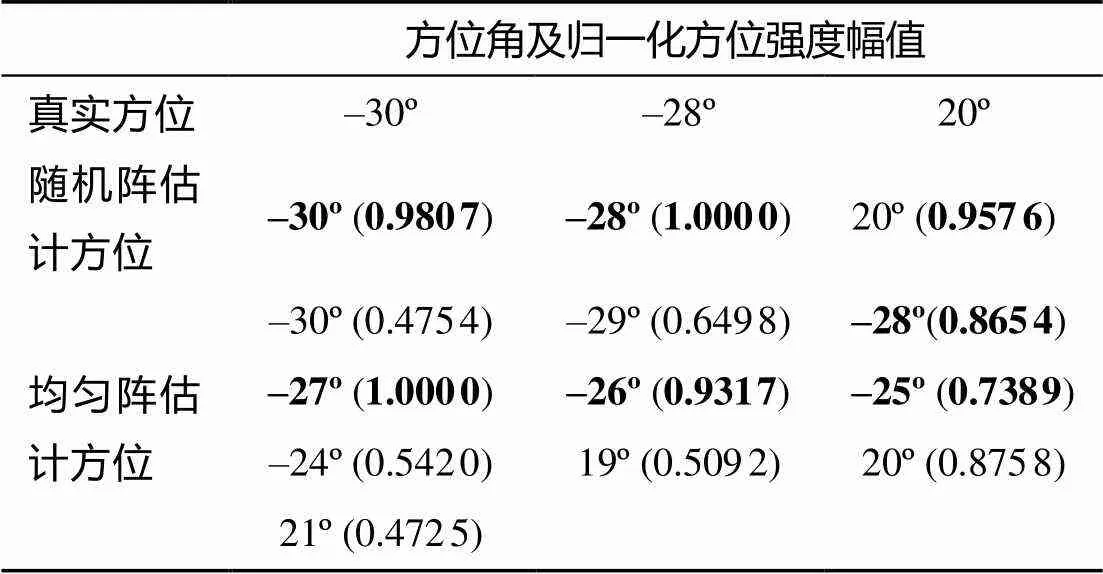
表1 随机阵列和均匀阵列估计的方位角及强度幅值

3.3 基于CS的目标方位估计算法

由1.1节中的分析可知, 水下目标信号源的个数相对于探测空间中的所有离散方位角数目来说是稀疏的, 所以目标方位角的估计问题实际上是一个稀疏信号的重构问题。基于OMP方法, 目标源信号支集重构方法的流程设计如下。

3) 基于OMP的稀疏信号重构

以下在不同的条件下, 通过仿真验证以上设计的随机声呐阵列和基于CS的水下目标方位估计算法的性能。为了显示估计方法的效果, 同时对MUSIC算法进行了对比仿真, 基本仿真条件与3.2节中相同。表2~4中的数据含义同表1。

仿真1: 目标源信号低信噪比、不相干、方位集中。假设4个远场目标的方位角分别为–30°, –28°, –26°和30°, 单个信源的信噪比均为–5 dB。仿真结果如图6和表2所示。从图中可以看出, 2种方法都准确估计出了目标的方位。但基于MUSIC的方法中出现了几个伪相。由表2中的数据可以看出, 2个比较明显的方位角是–4°和47°。这显然与实际情况不符。

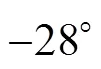
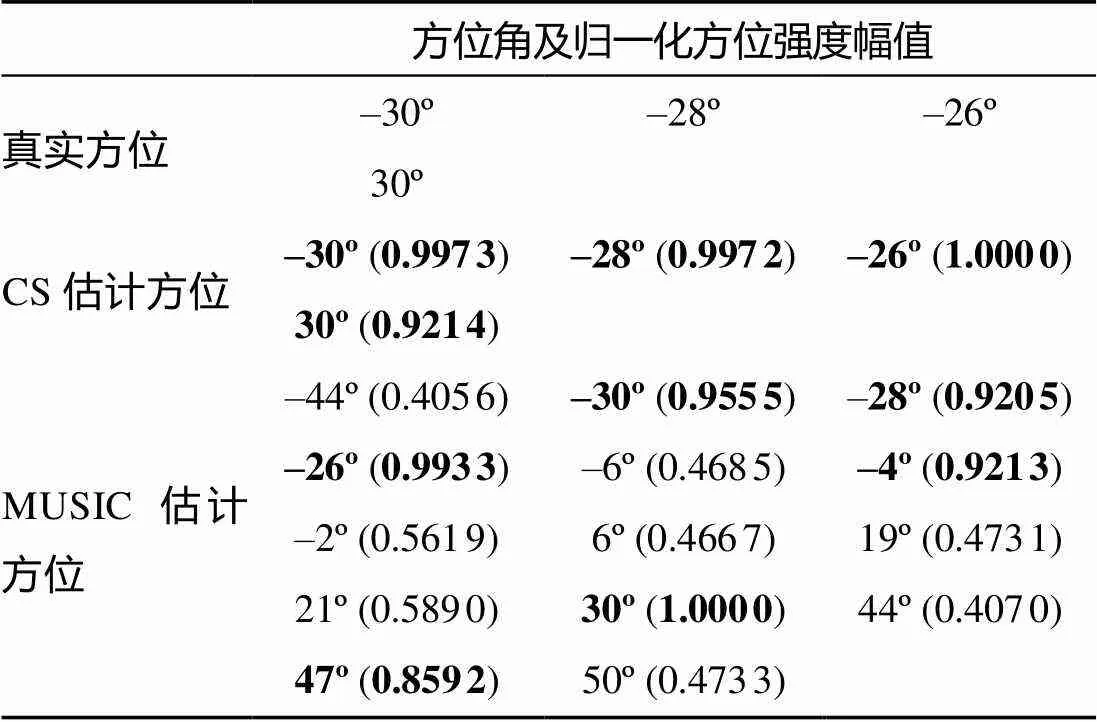
表2 仿真1估计的方位角和强度幅值

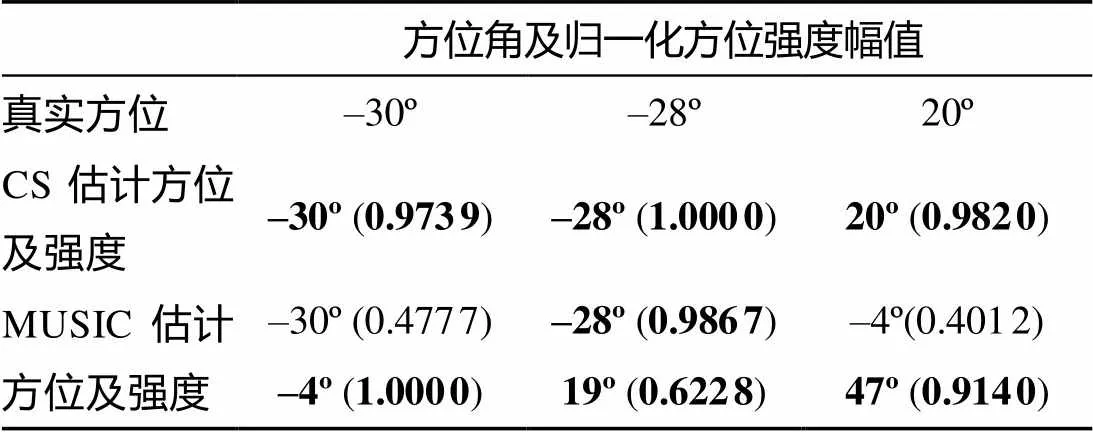
表3 仿真2估计的方位角和强度幅值

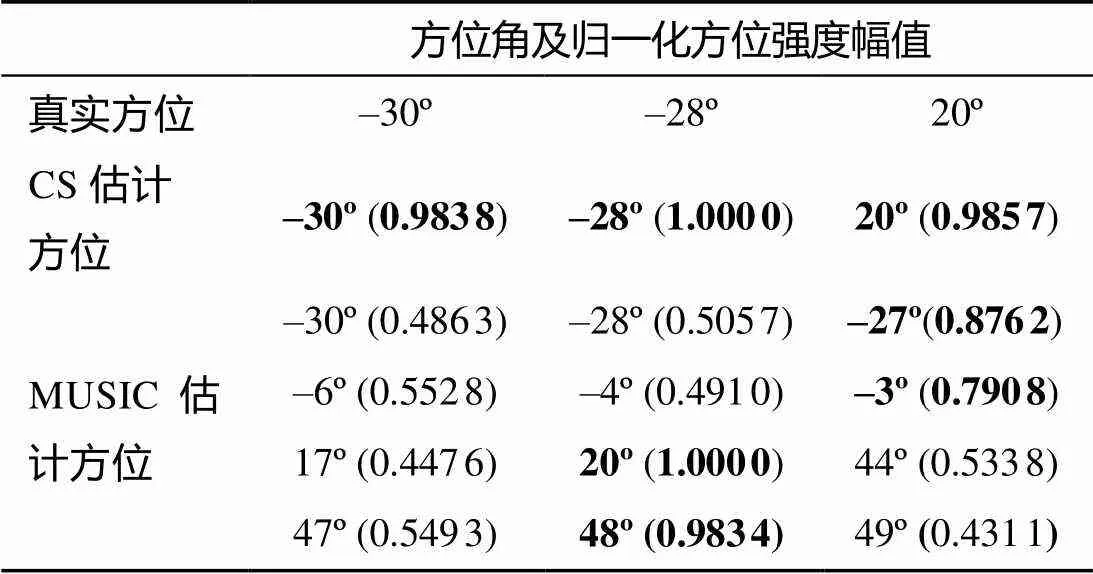
表4 仿真3估计的方位角和强度幅值

4 结束语

对于水下目标的方位估计问题, 设计了阵元稀疏且随机分布的声呐阵列, 同时设计了基于CS理论的目标方位估计算法。在低信噪比的情况下, 对设计的声呐阵列信号和方位估计方法进行了仿真, 结果表明:

1) 稀疏阵元的声呐阵列是可行的, 采用阵元随机分布线阵列估计的目标方位结果准确, 但阵元间距均匀分布情况下, 对方位集中的目标分辨力差, 不能分辨多个目标;

2) 对于稀疏随机阵列, 在低信噪比、目标源信号彼此相干、目标方位集中的情况下, 基于CS的方位估计方法均能准确分辨多个目标的方位, 但传统未作任何改进的MUSIC算法无法分辨方位集中且信源相干的目标。

关于声呐阵列的设计, 文中只是从节约制造成本和数据处理成本探讨一种稀疏阵元间距的可能性, 仿真结果验证了结论的正确性。在实际的应用中, 当需要处理的阵列数据量过大时, 按照文中的结论, 可以随机选择其中的部分阵列数据进行处理即可, 这将大大提高数据处理的效率。文中提出的水下目标方位估计方法不仅可以用于声呐, 还可以应用于雷达、无线电、地震、超声成像等多个领域。

[1] 王永良, 陈辉, 彭应宁, 等.空间谱估计理论与算法[M].北京: 清华大学出版社, 2004.

[2] Kumaresan R, Tufts D W.Estimating the Angles of Arrival of Multiple Plane Waves[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, 19(l): l34-139.

[3] Zhang Hong-mei, Gao Zhen-guo, Chen Ming-jie, et al.Estimation for Underwater Targets with Sparse Sonar Array[J].International Journal of Advancements in Computing Technology, 2013, 5(8): 507-514.

[4] Zhang Hong-mei, Sun Xi-wei, Chen Ming-jie.Research on Linear Sparse Sonar Array for Targets Azimuth Bearing Estimation[C]//IEEE International Conference on Mechatronics and Automation, Harbin: IEEE, 2016: 122- 127.

[5] Donoho D L.Compressed Sensing[J]. IEEE Transac- tions on Information Theory, 2006, 52(4): 1289-1306.

[6] Donoho D L, Elad M, Temlyakov V N.Stable Recovery of Sparse over-complete Representations in the Presence of Noise[J].IEEE Transactions on Information Theory, 2006, 52(1): 6-18.

[7] 石光明, 刘丹华, 高大化, 等.压缩感知理论及其研究进展[J].电子学报, 2009, 37(5): 1070-1081.Shi Guang-ming, Liu Dan-hua, Gao Da-hua, et al.Advances in Theory and Application of Compressed Sensing[J].Acta Electronica Sinica, 2009, 37(5): 1070-1081.

[8] Schmidt R O.Multiple Emitter Location and Signal Parameter Estimation[J].IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280.

[9] Malioutov D, Çetin M, Willsky A S.A Sparse Signal Reconstruction Perspective for Source Localization with Sensor Arrays[J].IEEE Transactions on Signal Processing, 2005, 53(8): 3010-3022.

[10] 郭艳芬, 张红梅, 冯素芬.一种基于压缩感知的目标DOA估计方法[J].北京工业职业技术学院学报, 2013, 12(3): 58-62.Guo Yan-fen, Zhang Hong-mei, Feng Su-fen.A CS-based DOA Estimation Method for Submarine Target[J].Journal of Beijing Polytechnic College, 2013, 12(3): 58-62.

[11] 张峰.水下目标方位估计方法研究[D].哈尔滨: 哈尔滨工程大学, 2013.

Underwater Target Azimuth Estimation Based on CS and Random Sonar Array

ZHANG Hong-mei, CHEN Ming-jie, LIU Hong-dan, SUN Xi-wei

(College of Automation, Harbin Engineering University, Harbin 150001, China)

The problem of underwater target azimuth estimation of linear passive sonar is studied.For the data processing algorithm, considering the fact that the underwater target's orientation relative to all possible detection directions is sparse, the compressive sensing(CS) technology is adopted to design a method for estimating the underwater target azimuth.As for the structure of linear sonar, according to the mutual incoherence property(MIP) condition in CS theory, a kind of linear sonar array with sparse and randomly distributed elements is constructed.Simulation results show that the designed sonar array, combined with the target azimuth estimation method based on CS, can accurately identify the targets with concentrated spatial orientation in the condition of low signal-to-noise ratio underwater, and the targets with coherent source signal.

underwater target; azimuth estimation; compressive sensing(CS); random sonar array

TJ630.34; U674.941; TB566

A

2096-3920(2018)06-0588-08

10.11993/j.issn.2096-3920.2018.06.013

2018-10-08;

2018-11-29.

张红梅(1973-), 女, 博士, 副教授, 主要研究方向为信号处理、导航技术及随机系统滤波技术.

张红梅, 陈明杰, 刘洪丹, 等.基于CS和随机声呐阵列的水下目标方位估计[J].水下无人系统学报, 2018, 26(6): 588-595.

(责任编辑: 陈 曦)