花岗岩中实测球面波粒子速度的时域和频域分析

卢 强，王占江，朱玉荣，丁 洋，郭志昀，张永伟

(西北核技术研究所，西安710024； 强动载与效应重点实验室，西安710024)

球面波实验是研究波传播规律和3维应力-应变条件下介质动力学特性的重要手段之一[1-4]，被国内外众多学者所关注。美国进行了大量的球面波实验研究，涉及的介质有凝灰岩、花岗岩、页岩、冲积土、混凝土等[5-9]。Larson对球面波加载下岩石特性与爆炸能量之间的耦合关系进行了大量的研究[5-7]。Nagy采用0.375 g的太安球形装药对低孔隙率脆性岩石中的球面波传播特征进行了研究，分析了围压、孔隙率、含水量等因素对波传播演化的影响[8]，指出了实测球面波径向粒子速度波形与采用传统的理想弹性假设方法预测的粒子速度波形，在峰值和脉宽上均存在较大差异，但研究中未考虑波传播衰减过程中对频率的依赖性。James等报道了φ1 829 mm×1 829 mm混凝土样品中454 g TNT炸药球爆炸加载实验[9]，目的是通过测量球形爆炸下快速膨胀空腔周围的应力和粒子运动参数，验证与评估混凝土中侵彻和爆炸效应的计算模型。1985年，中国科学院武汉岩土力学研究所开展了球面波化爆实验[10]，建立了以∏形电磁粒子速度计和压电晶体应力计为测量手段、以微秒电雷管起爆直径30 mm铸装炸药球作波源的室内岩石球面波化爆实验装置。王占江等建立了0.1 g TNT的球面波实验装置，并获得多种介质中球面波径向粒子速度数据[11]。卢强等利用实测球面波数据，结合黏弹性理论对球面波在黄土及有机玻璃介质中的传播特性进行了分析[12-18]。

本文以0.125 g TNT、直径为5 mm的炸药球填实爆炸加载下花岗岩中实测球面波数据为基础，给出了球面波在花岗岩中传播演化的时域特征，结合黏弹性球面波传播理论对球面波传播的频率特征进行了近似分析，并对分析结果进行了评估。

1 花岗岩中球面波实验简介

花岗岩是一种典型的介质材料，属于火成岩。花岗岩主要成分为钾长石(40%～45%)、酸性斜长石(30%～35%)、石英(18%～22%)、黑云母(2%～5%)、磁铁矿(0.1%～1%)等，矿物颗粒直径为0.2～5 mm。用于球面波实验的花岗岩样品是从米级尺度的新鲜岩石上切割成型后再由专门的岩石加工设备精加工而成[1]。本文所用的花岗岩取自华山[19]，花岗岩样品的密度为2.60 g·cm-3，尺寸为φ276 mm×300 mm，爆炸源为0.125 g TNT精密微型炸药球。考虑到样品边界反射波对粒子速度计的影响，离爆心最远的粒子速度计设置在半径为120 mm处。本文主要分析填实爆炸条件下，花岗岩半径为10～120 mm时的球面波数据。球面波实验示意图，如图1所示。

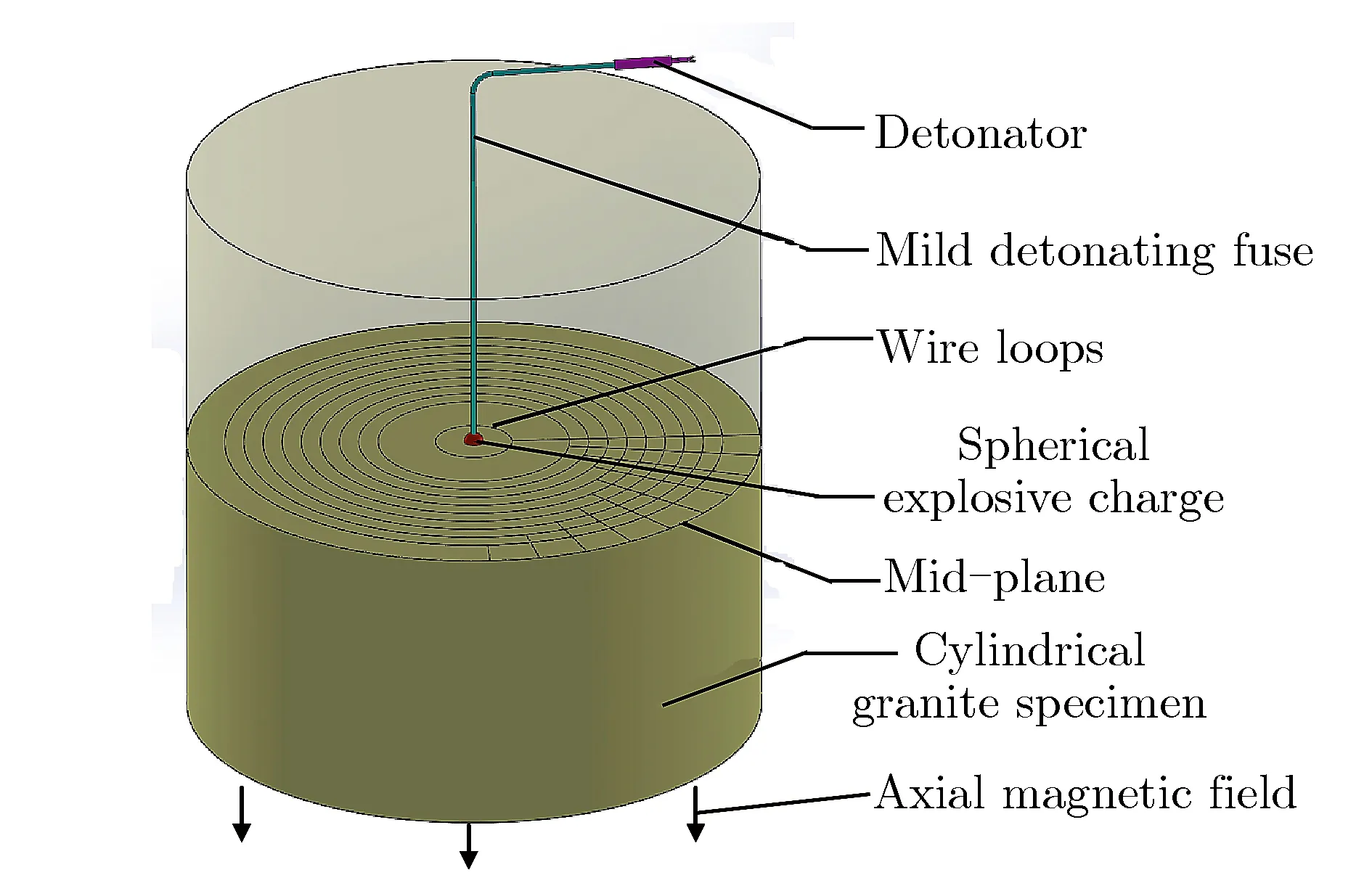
图1球面波实验示意图Fig.1Schematic of spherical wave experiment

2 花岗岩中球面波传播的时域特征

图2--图5给出了测点半径为10～25 mm，30～50 mm，60～90 mm，100～120 mm时实测的球面波径向粒子速度曲线。

图2半径为10～25 mm时，花岗岩中实测的粒子速度曲线Fig.2Measured particle velocities in granite (r=10～25 mm)

图3半径为30～50 mm时，花岗岩中实测的粒子速度曲线Fig.3Measured particle velocities in granite(r=30～50 mm)

图4半径为60～90 mm时，花岗岩中实测的粒子速度曲线Fig.4Measured particle velocities in granite(r=60～90 mm)

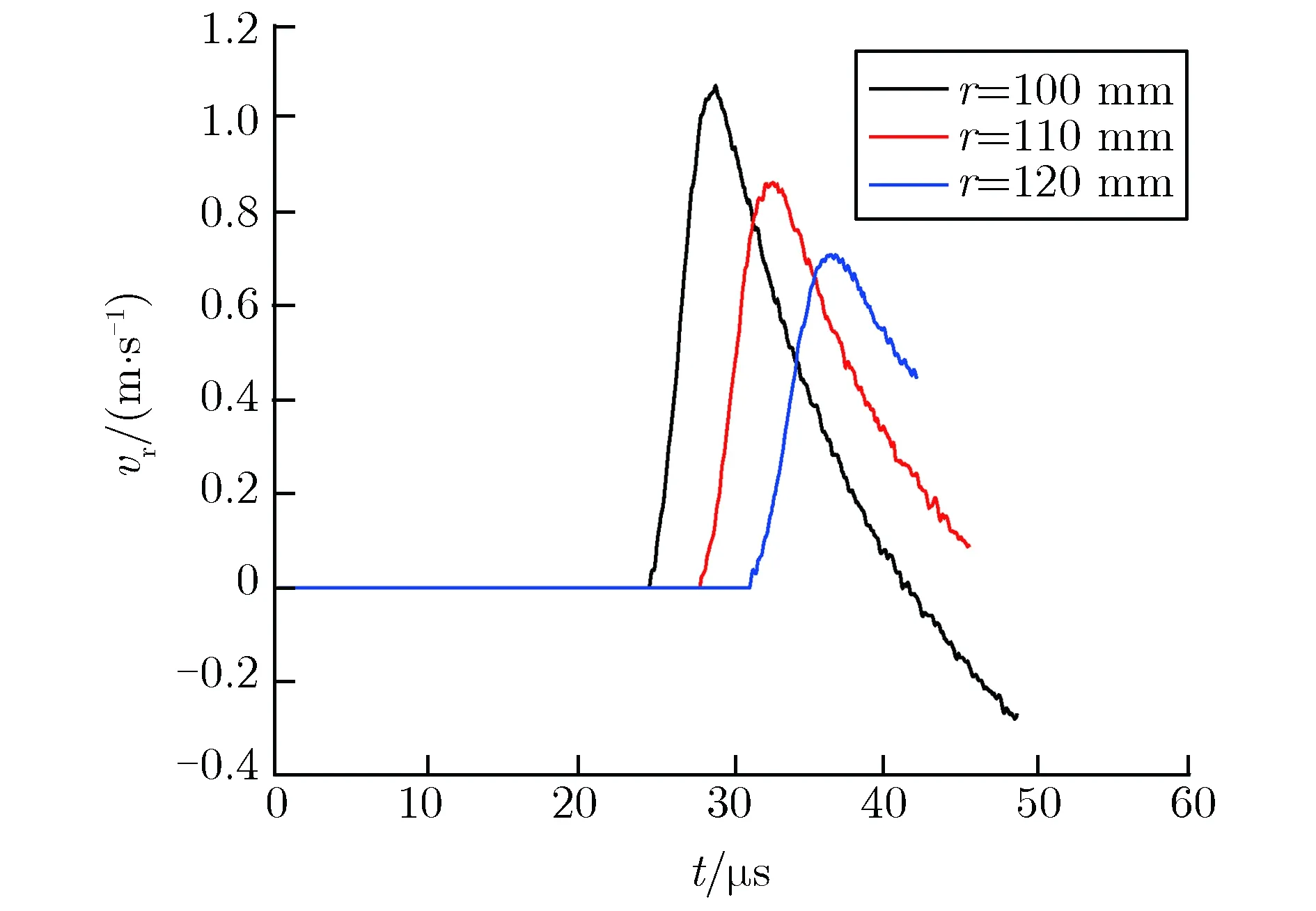
图5半径为100～120 mm时，花岗岩中实测的粒子速度曲线Fig.5Measured particle velocities in granite(r=100～120 mm)

图6和图7分别给出了花岗岩中球面波粒子速度峰值vmax和比例粒子位移峰值umax随比距离R(R=r/Q1/3)的变化规律。同时，对实验数据进行了单段线性拟合和双段线性拟合，拟合结果一并绘于图中。单段线性拟合公式为

(1)

(2)

双段线性拟合公式为

(3)

(4)

从图6和图7可以看出，粒子速度峰值和比例粒子位移峰值均随波传播距离的增加而减小；单段线性拟合结果和实验结果偏差较大，而双段线性拟合结果与实验结果符合较好。从双段线性拟合结果可以看出：粒子速度峰值和比例粒子位移峰值在不同区域内的衰减规律是不同的，离爆心较近的区域衰减较慢，离爆心较远的区域粒子衰减较快。可见，花岗岩中球形波的衰减不仅包含了传播距离的几何衰减，还包含其非线性动力学特性引入的黏性衰减。

图6花岗岩中粒子速度峰值随比距离的变化Fig.6Peak values of particle velocity vs. scaled distance in granite

图7花岗岩中比例粒子位移峰值随比距离的变化Fig.7Peak values of scaled particle displacement vs. scaled distance in granite

图8为0.125 g TNT炸药球填实爆炸下，花岗岩中实测的球面波径向粒子速度波形的时间特征随比距离的变化关系。可以得到：在测点半径10 mm处，波形上升沿ΔTr约为0.5 μs；在测点半径120 mm处，ΔTr约为5.3 μs；二者相比，ΔTr展宽了约10倍。另外，ΔTr、波形半高宽ΔT1/2及波形正向脉宽ΔT+均有随着比距离增加而增加的趋势。球面波在花岗岩中传播的展宽效应也反映了其非线性动力学响应的复杂性，基于理想弹性假设的波传播理论，无法对其波形的传播演化规律进行合理解释。

图8花岗岩中粒子速度波形的时间特征随比距离的变化Fig.8Time features of particle velocity waveforms vs. scaled distance in granite

3 花岗岩中球面波粒子速度的频率响应函数

3.1 粒子速度的频率响应函数典型特征

按照粒子速度的频率响应函数定义，可以给出以测点半径r1、r2处球面波径向粒子速度为输入量的频率响应函数的计算公式为[13, 18, 20]

(5)

在对粒子速度的频率响应函数进行分析时，如果单独分析幅频特性会损失相频特性的信息，只分析相频特性同样也会损失幅频特性的信息。鉴于粒子速度响应函数Hvr(r2,r1，ωi)的实部和虚部均包含了幅频特性及相频特性信息，因此，将其分别作为分析对象。实部和虚部可以分别写为

Re[Hvr(r2,r1，ωi)]=

|[Hvr(r2,r1，ωi)| cos[φvr(r2,r1，ω)]

(6)

Im[Hvr(r2,r1，ωi)]=

|[Hvr(r2,r1，ωi)| sin[φvr(r2,r1，ω)]

(7)

式中，|[Hvr(r2,r1，ωi)|描述了幅频特性；φvr(r2,r1，ω)描述了相频特性。φvr(r2,r1，ω)的计算公式为

φvr(r2,r1，ω) =unwrap{angle[Hvr(r2,r1，ωi)]}

(8)

式中，angle为辐角函数；unwrap为相位展开函数，其功能是检查数据相位跳变并纠正其跳变。

按照式(5)的定义，图9和图10分别给出了r1为35 mm，r2为50 mm时，花岗岩中粒子速度的频率响应函数的实部和虚部随圆频率的变化曲线，并采用幅值按指数衰减的正弦振荡函数曲线进行了拟合，拟合结果一并在图中给出。拟合函数为

Re[Hvr(r2,r1，ωi)]=Ae-ω/ω0sin[π(ω-ωc)/ω1]

(9-1)

Im[Hvr(r2,r1，ωi)]=Ae-ω/ω0sin[π(ω-ωc)/ω1]

(9-2)

式中，A代表拟合函数的幅值；ω0为延迟因子，rad·s-1；ω1和振荡周期相关；ωc和波形的初始相位相关。

从图9和图10可以看出，实部和虚部的振荡幅值均随着圆频率的增加而逐渐降低；拟合的结果在ω>1.0×106rad·s-1的高频衰减部分与实验曲线符合程度较好，在ω<1.0×106rad·s-1的低频部分与实验曲线符合较差。

图9花岗岩中粒子速度的频率响应函数的实部随圆频率ω的变化曲线(r1=35 mm，r2=50 mm)Fig.9The real part of the particle velocity response function in granite(r1=35 mm，r2=50 mm)

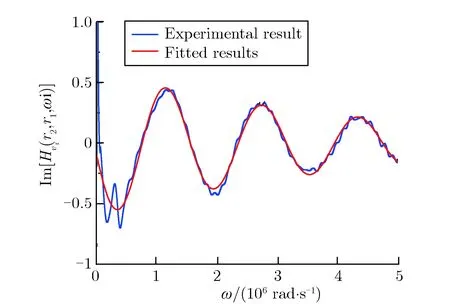
图10花岗岩中粒子速度的频率响应函数的虚部随圆频率ω的变化曲线(r1=35 mm，r2=50 mm)Fig.10The imaginary part of the particle velocity response function in granite(r1=35 mm，r2=50 mm)

3.2 粒子速度的频率响应函数有效频段的估计方法

理论上，任何位置的球面波粒子速度信号均应包含由源激发的所有频率信息，受到介质黏性以及几何发散的影响，粒子速度的部分频段受到抑制的程度高，而有些频段受到抑制的程度低，但用任何两个位置的粒子速度信息均应能给出粒子速度所有频率对应的响应值。对于球面波实验，球面波传播过程中其频率成分不断发生变化，部分频段的粒子速度信息由于粒子速度计无法响应或响应精度降低、测试记录设备精度不足、样品尺寸小导致信号低频成分未能充分展现等一系列原因，将影响后续的数据分析精度，这就要求对利用实测粒子速度分析粒子速度的频率响应函数的有效频段进行评估。

按式(8)给出的当r1为15 mm，r2为20 mm和r1为40 mm，r2为50 mm时的相频特性曲线，如图11所示。可以看出，当r1为15 mm，r2为20 mm时，相频特性曲线在ω>1.15×107rad·s-1(对应频率f>1.83 MHz)时开始出现异常变化，这说明用该位置实测粒子速度计算的频率响应函数的有效频段的上限ωmax为1.15×107rad·s-1(fmax为1.83 MHz)。同理，用r1=40 mm，r2=50 mm位置实测粒子速度计算的ωmax为5.64×106rad·s-1(fmax为0.90 MHz)。对比图11中近区和远区的相频特性曲线，可以发现，远区粒子速度的频率响应函数的有效频段上限降低，这是因为随着波的传播，远区的粒子速度由于介质耗散、几何发散等原因导致高频粒子速度信息丧失，高频成分信号弱、空间电磁噪声、记录设备精度等均会对数据获取精度造成影响。

图11花岗岩中粒子速度的典型相频特性曲线Fig.11Typical phase-frequency characteristic of particle velocity in granite

粒子速度的频率响应函数的有效频段下限ωmin或fmin受多种因素的影响，包括样品尺寸小导致的低频信号发展不充分、空间电磁噪声对低幅度粒子速度信号的掩盖等，对其评估较为困难。本文利用粒子速度信号的采样频率及实际采样点数，近似给出有效频段下限值的确定方法。

本文花岗岩球面波实验中的信号采样频率S为50 M·s-1，扣除边界反射波影响后测试的有效持续时间为50～60 μs，L约为2 500。按照傅里叶理论分析，频率的分辨率近似为

(10)

由式(10)可推断，粒子速度的频率响应函数有效频段的下限fmin应高于信号的频率分辨率Δf。由此可得，在本文的测试区域内，粒子速度的频率响应函数的有效频段应满足：

10 kHz=Δf≤fmin

(11)

这里需指出的是，fmax和采用哪两个位置的粒子速度信号直接相关，fmin是较为粗略的估计，总体上看式(11)只是对有效频段的近似估计，便于工程上参考使用。

3.3 粒子速度的频率响应函数的高频近似分析

考虑黏弹性条件下，式(5)的幅频及相频特性的理论公式可写为[13, 20]：

|Hvr(r2,r1,ωi)|=

(12)

φvr(r2,r1,ω)=-k(ω)(r2-r1)+

(13)

式(12)和(13)中，α(ω)和k(ω)分别为频率衰减因子和波数，它们共同构成波传播系数β(ω)。β(ω)可写为[13]

(14)

式中，C(ω)=ω/k(ω)为相速度。波传播系数β(ω)控制波传播过程中的衰减及形状变化。

式(12)和式(13)是非线性方程，为满足工程需要，可做近似分析。当k(ω)满足：

且k(ω)≫α(ω)

(15)

则可将式(12)和式(13)近似为

(16)

φvr(r2,r1,ω)=-k(ω)(r2-r1)

(17)

以r1=15 mm，r2=20 mm时得到的粒子速度的频率响应函数为例，按上述分析可得其有效频段的估计值为

10 kHz=Δf≤fmin

(18)

按时域给出的波传播速度估计值c≈5 000 m·s-1计算，波数的最大值kmax(ω)为

(19)

由式(19)可以看出，在有效频段接近fmax的频率区间，k(ω)满足式(15)。另外，由文献[4]给出的方法，利用式(16)及两个不同位置的粒子速度峰值，估计出高频段的α(ω)约为21.7，也满足式(15)。此高频条件下，粒子速度的频率响应函数的实部和虚部可以近似写为

cos[-k(ω)(r2-r1)]

(20)

sin[-k(ω)(r2-r1)]

(21)

由式(20)和式(21)可知，粒子速度的频率响应函数实部和虚部的振荡特性主要由k(ω)的变化特征和传播距离r2-r1决定，其衰减特征主要由α(ω)的变化特征和r2-r1决定。在k(ω)和α(ω)确定的条件下，r2-r1控制着粒子速度的频率响应函数实部和虚部的衰减和振荡特性。把式(9)同式(20)及式(21)进行对比，可以给出：

(22)

(23)

从式(22)和式(23)可以看出：频率衰减因子α(ω)和波数k(ω)均与圆频率ω近似成线性关系，其比例系数分别为κ和λ，则

β(ω)=α(ω)+k(ω)i=κω+λωi

(24)

在测点半径为15～70 mm内布置粒子速度计测量粒子速度信息，并计算κ，λ，fmax，结果如表1所列。

表1基于实测粒子速度计算的κ，λ，fmax

Tab.1κ，λ，fmaxcalculatedwithmeasuredparticlevelocities

r1/mmr2/mmκ/(10-5 s·m-1)λ/(10-4 s·m-1)fmax/MHz15201.002.191.8320251.051.981.7725300.682.211.6230352.032.201.6135403.362.471.3340501.792.670.9050603.522.750.6960704.102.910.49

从表1可以看出，由不同位置的实测粒子速度给出的fmax随波传播距离的增加而逐渐降低，这反映了波传播过程中高频成分的耗散。κ和λ在不同频段内的拟合值不同，这表明α(ω)和k(ω)在不同频段内变化的快慢不同，反映了球形应力波在花岗岩中传播的复杂性。

4 讨论

由式(3)可知，在测点半径为10～120 mm的测试区域内，近似以r为28 mm(R为56 m·kt-1/3)为分界点，靠近爆心的区域内粒子速度峰值的幂衰减指数为1.46，远离爆心的区域内粒子速度峰值的幂衰减指数为2.60。由表1可以看出，由r1和r2均小于30 mm区域内的实测粒子速度给出的频率衰减因子的比例系数κ整体上明显小于r1和r2均大于30 mm区域内的κ值。时域和频域的分析结果都表明，在半径r为30 mm(R为60 m·kt-1/3)附近时，球面波粒子速度峰值的衰减出现了转折。另外，上述结果也表明：本文提出的球面波频域分析方法给出的结果和时域的结果在物理上是相符的。

为对本文提出的球面波传播的频域分析方法进行评估，利用表1给出的波传播系数及r1处粒子速度作为输入量，计算r2处的粒子速度，并将其和实测粒子速度进行比较。按照粒子速度的频率响应函数的定义，r2处粒子速度的频域计算公式可以写为[20]

(25)

vr(r2，t)=

(26)

式(26)中，N为粒子速度频域对应的点数。

将式(26)中的波传播系数β(ω)分别取为

β(ω)=κω+λωi

(27)

β(ω)=λωi

(28)

式(27)表示利用r1处粒子速度并结合式(26)反演粒子速度时，同时考虑了波传播过程中衰减因子和波数的影响，而式(28)则没有考虑衰减因子的影响。

图12预测的粒子速度波形和实测波形的对比(r1=15 mm，r2=20 mm)Fig.12Comparison between the predicted particle velocity waveform and the measured waveform (r1=15 mm，r2=20 mm)

图12和图13分别给出了r1=15 mm，r2=20 mm和r1=20 mm，r2=25 mm时的实测粒子速度曲线同预测的粒子速度曲线的对比。可以看出，采用式(27)反演的粒子速度峰值比采用式(28)反演的粒子速度峰值更接近实测结果，这反映了介质黏性对波衰减的影响。还可以看出，无论是基于式(27)还是基于式(28)的假设，反演的粒子速度波形和实测粒子速度波形之间均有较大的差别。

图13预测的粒子速度波形和实测波形的对比(r1=20 mm，r2=25 mm)Fig.13Comparison between the predicted particle velocity waveform and the measured waveform (r1=20 mm，r2=25 mm)

图14给出了花岗岩中粒子速度峰值预测结果和实测结果的对比。可以看出，本文给出的球面波传播系数的线性近似计算方法考虑了波传播过程中衰减因子的影响，与传统的局部理想弹性假设方法[8]相比，提高了对粒子速度峰值的预测精度，但对粒子速度波形演化过程中形状的变化，其预测能力不高。解决这个问题的关键是利用式(5)直接给出粒子速度的频率响应函数的实验结果，进而求解式(12)和式(13)构成的非线性方程组，确切获得波传播系数β(ω)随频率的变化，这部分内容将在后续研究中予以关注。

图14花岗岩中粒子速度峰值预测结果和实测结果的对比Fig.14Comparison of peak values of particle velocity obtained by predicted and measured in granite

5 结论

本文分析了0.125 g TNT、直径为5 mm的炸药球填实爆炸加载下花岗岩中球面波传播的时域特征，提出了一种基于黏弹性假设的球面波粒子速度频域分析方法，得到如下结论：

1)对花岗岩中粒子速度峰值和比例粒子位移峰值进行对数坐标下的线性拟合分析，结果表明粒子速度峰值和比例粒子位移峰值在靠近爆心的区域衰减慢，远离爆心的区域衰减快；

2)从花岗岩中实测球面波粒子速度波形的时域和频域分析结果可知，在测点半径约为30 mm(比距离约为60 m·kt-1/3)处，粒子速度峰值的衰减规律出现由慢变快的转折；

3)在高频近似分析下，花岗岩中频率衰减因子α(ω)和波数k(ω)均与圆频率ω近似成线性关系，但由不同相邻位置实测的粒子速度信息得到的α(ω)和k(ω)各不相同；

4)球面波传播系数的线性近似处理方法对波传播演化过程中波形形状的预测精度不高，但相比于传统的局部理想弹性假设方法，本文的近似处理考虑了波传播过程中衰减因子的影响，可以提高粒子速度峰值的预测精度。