基于L1自适应着舰纵向控制与特性分析

，，吉宽，

(1.西北工业大学 自动化学院, 西安 710072; 2.空军试飞局,西安 710089)

0 引言

由于海浪和舰尾流等环境因素对舰载机会产生极大影响，这会严重影响舰载机的着舰精度和成功率。因此，在着舰最终阶段舰载机必须克服由海浪引起各种舰尾气流所带来的不利影响。这些影响因素的存在就对舰载机着舰控制系统的快速性和抗干扰性提出了更高的要求。L1自适应控制方法通过引入低通滤波器将快速自适应与鲁棒性解耦，能够保证系统在实现快速自适应的同时保证良好的鲁棒性。因此，基于此方法来设计舰载机纵向自动着舰控制律能够很大程度上地抑制舰尾气流对其造成的不利影响。L1自适应控制方法最初是由Cao Chengyu和Naria Hovakimyan2006年在美国控制会议上提出[1]。L1自适应方法在翼面损伤飞机控制[2]、微小型飞行器(MAV)的控制[3]、垂尾损伤的运输机控制[4]、NASA弹性运载火箭控制[5]、舰载机侧向自动着舰引导控制[6]等方面都有广泛的研究。特别的，在GTM缩比模型[7]、X-29[8]等飞机上已经完成试飞验证。一般的自适应控制方法会存在容易引起“因自适应增益过大而导致系统发生振荡”的问题。由于L1自适应控制结构中存在低通滤波器。因此，控制信号中由于快速性产生的高频信号会被滤除，这样就能使系统在保证快速跟踪指令信号的同时舵面不产生高频振荡，进而解决一般自适应控制方法容易引起系统振荡的问题。与传统控制律相比，L1自适应控制方法的快速性更好，于此同时，基于此方法设计的控制系统具有良好的瞬态和稳态性能。基于上述L1自适应控制方法的应用特点，采用此方法设计的自动着舰控制系统既能使舰载机在快速地跟踪上指令信号的同时使舵面不发生振荡，还能够在很大程度上地抑制舰尾气流对其的不利影响。本文基于L1自适应控制方法设计舰载机纵向自动着舰控制律，并通过仿真验证所设计控制律的鲁棒性和快速性。最后定性和定量地分析了不同风速的舰尾流对纵向着舰点的影响。

1 舰载机着舰控制问题

1.1 着舰控制律结构

根据舰载机的特点以及着舰环境模型，将受到舰尾流等环境因素影响下的舰载机着舰模型方程化成如下形式：

(1)

其中:x=[v,α,q,θ]T为可观测的舰载机的状态量；v,α,q,θ分别表示速度、迎角、俯仰角速率和俯仰角；B,C为已系统的输入、输出矩阵；A∈R4×4为系统矩阵；w∈R2×2是未知输入增益；θ(t)∈R2×4为未知时变参数向量，此处主要是舰尾流对舰载机状态量的影响；δ(t)∈R2×1是时变干扰；y(t)∈R为系统输出；u=[δe,δT]为控制信号，分别表示升降舵和油门。

本文所设计的自动着舰控制律主要分为内环和外环两部分。内环采用基于L1自适应俯仰姿态保持控制和自动油门控制系统；外环采用基于PIDD形式的制导控制。内环采取的控制方案是：用L1自适应控制方法来控制舰载机俯仰角θ，同时自动油门系统采取基于迎角恒定的形式。其原因是迎角恒定有利于增强下滑轨迹响应。制导回路采用PIDD(比例、积分、微分、二次微分)形式的控制律，二次微分为系统提供了额外的相角超前，改善了系统滞后的问题[9]，同时也提高了系统的精度。纵向自动着舰系统控制结构如图1所示。

图1 纵向自动着舰系统控制结构

1.2 舰尾流模型

舰尾气流是影响舰载机着舰精度的主要因素。因此，在设计自动着舰控制律的过程中必须予以考虑。在美国MIL-F-8785C军用标准中，将舰尾气流分为4个部分[10]，其组成为：(a)低空(海面)自由大气紊流记为u1、v1、w1；(b)稳态航母尾流扰动u2、w2，这种气流是航母逆风行驶，空气从平坦的舰尾流出所形成的。其特点是在舰尾产生一种类似于“雄鸡”形状的尾流，在舰尾主要表现为向下的有效风力，随着距离航母舰尾越远，向下的风力就越小，随后改为向上的风力；(c)航母纵向运动引起的周期性扰动u3、w3，这种气流是由甲板俯仰运动产生的风力而产生的，它随着航母纵摇频率、大小、甲板风的风速以及舰载机离舰距离变化而变化；(d)随机航母尾流扰动u4、v4、w4，这种气流和舰尾流中的随机分量，与舰载机与航母的距离有关。总的大气扰动分量为u、v、w。其计算公式如下：

u=u1+u2+u3+u4

v=v1+v4

w=w1+w2+w3+w4

(2)

式中，u、v、w分别为风速在机体轴x、y、z轴上的分量。

2 基于L1自适应方法的着舰控制律设计

2.1 基于L1纵向控制律设计

纵向控制回路由俯仰姿态保持系统和基于迎角恒定的自动油门系统组成。基于L1自适应控制方法的纵向控制律设计思想是：在舰尾流影响下，俯仰姿态系统控制舰载机的俯仰角，基于迎角恒定的自动油门系统始终保持基准迎角的α0不变。在着舰的过程中，基于迎角恒定的自动油门系统不仅能够保持速度不变，而且能增强Δγ对Δθ的跟踪响应，文献[11]和文献[12]给出相关证明。纵向控制系统模型可写成如下所示：

(3)

u(t)为控制输入，可分为两部分：

u(t)=um(t)+uad(t)，um(t)=-KTx(t)

(4)

其中:第一部分um(t)是线性控制器产生的控制信号，使得Am=A-BKT。Am是根据期望飞行品质的要求设计出的Hurwitz矩阵。第二部分uad(t)是L1自适应控制产生的控制信号。因此，式(3)可变为：

(5)

设计状态观测器：

(6)

自适应律采用投影算子，如式(7)。具体介绍见参考文献[13]:

(7)

控制器结构为:

(8)

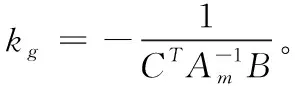
2.2 L1自适应控制器稳定性分析

根据被控对象和参考模型可以得到误差的动态:

(9)

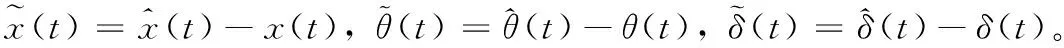
选取Lyapunov函数:

(10)

对其求导并化简，根据自适应律中的投影算子可得:

(11)

如果存在:

其中:

从而:

(12)

(13)

(14)

从而可以得到:

(15)

状态量的跟踪误差收敛于零的一个区域内，并且自适应增益Γ越大，系统的状态误差越小。

2.3 自动着舰制导律设计

在基于L1自适应姿态保持系统和基于迎角恒定的自动油门控制系统的基础上，纵向制导律采用PIDD形式的控制律，如式(16)：

(16)

利用L1自适应控制的特殊结构和鲁棒性来克服舰尾气流对舰载机的干扰，进而提高着舰精度。

3 仿真验证

选用某大型涡桨飞机为舰载机模型，配平高度为400 m；飞行速度为80 m/s。配平后状态量：θ=α=8.1°；油门开度0.313；升降舵为-11.2°。纵向状态量x=[v,α,q,θ]。纵向将极点配置为τ=[-8.466,-1.107,-0.305+0.26i,-0.305-0.26i]，低通滤波器选设计为：

(17)

假设最初舰载机距离航母5 288 m。初始高度为400 m。给定高度指令为斜率-3.5 m/s的斜坡信号(下沉率为-4.88 m/s)。舰载机着舰环境选取6级海况，风速选择40 ft/s。在着舰最后12.5 s(此刻距离航母约1 000 m)加入舰尾气流干扰。仿真结果如图2所示。

图2 仿真结果示意图

从仿真结果上来看，纵向经过约20 s跟踪上下滑指令信号。在舰载机距离理想着舰点960 m处(约69 s处)加入舰尾流，由于舰尾流的干扰直接作用于舰载机的迎角，这就使得原本稳定的迎角产生突变，高度等其余状态就也随之变化。所设计好的控制律立即开始抑制迎角变化并且纠正高度偏差，在加入舰尾流4 s后(73 s)高度误差被控制在±0.5 m之内，这一误差范围满足着舰精度要求(±1.5 m)。在着舰过程中，升降舵和油门都在正常范围内变化。

4 舰尾气流对着舰点的影响分析

航母纵向运动引起的稳态舰尾流u2、w2，周期性扰动u3、w3和随机航母尾流扰动u4、v4、w4都与风速有着极大的关系。因此，为了讨论和分析舰尾流对舰载机着舰点的影响，选取舰尾流风速为Vwind=30,40,50 ft/s分别进行仿真。由于舰载机距离航母960 m之内加入舰尾流干扰，为了便于观察，图3和图4只绘制出加入舰尾流后下滑轨迹和高度误差变化情况。

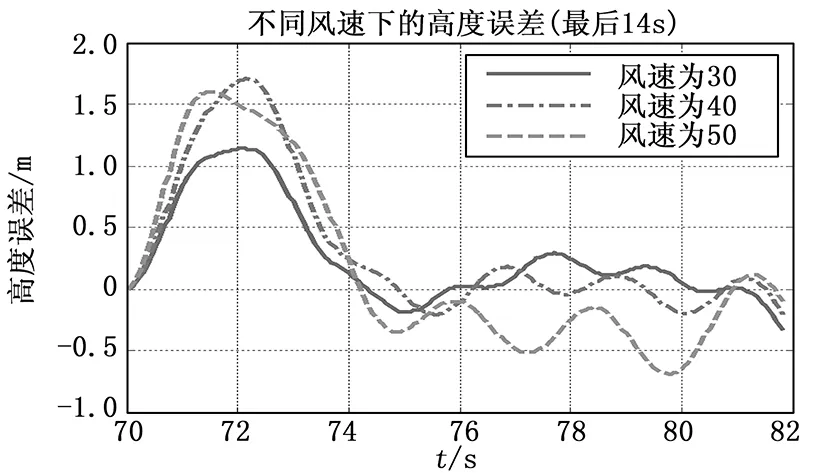
图4 不同风速下高度误差

从仿真结果来看，舰尾流的风速越大，舰载机的高度误差变化幅度就越大。总体说来，在加入舰尾流干扰4 s后，高度误差都被控制在±0.5 m之内。

为了进一步分析纵向着舰点的偏差与舰尾气流风速的关系，依旧选取Vwind=30,40,50 ft/s进行仿真。由于舰尾流中存在“随机性”因素，因此每组风速仿真50次，仿真结果如图5～7所示。

图5 风速为30 ft/s时，着舰点分布

图6 风速为40 ft/s时，着舰点分布

图7 风速为50 ft/s时，着舰点分布

从分布图中可以看出，纵向着舰点随舰尾流的“随机性”也在一定范围内呈现出“随机性”。得益于所设计自动着舰控制律较好的鲁棒性，着舰点“随机性”浮动的范围很小。统计纵向着舰点的均值和方差，如表1。

表1 不同风速下，纵向着舰点均值和方差

根据上表数值的变化，可以推测出纵向着舰点和舰尾流风速存在着一定的关系。为了证明这一猜想，这里采用“单因素方差分析法”。单因素方差分析法主要用于检验一种因素对实验是否产生影响。该方法具体原理见参考文献[14]。

首先，检验3组数据是否服从正态分布，经过检验三组数据都服从正态分布；其次，做出合理假设，H0:舰尾流风速对纵向着舰点存在显著性影响，H1: 舰尾流风速对着舰点不存在显著性影响。最后，统计上述仿真结果的数据，列出方差分析表。

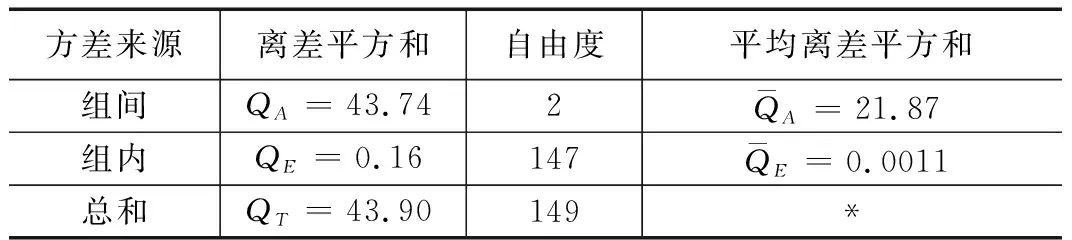
表2 舰尾流风速对纵向着舰点方差分析表

为了更进一步分析和讨论纵向着舰点随舰尾流风速变化的变化趋势。选取风速从10～50 ft/s进行仿真，绘制出纵向着舰点随不同风速的舰尾流的变化趋势图。

图8 纵向着舰点误差随舰尾流风速变化趋势图

从趋势图中明显可以看出，舰载机纵向着舰点误差会随着舰尾流风速的增加而增加。但是，由于所设计的基于L1自适应的自动着舰控制律具有良好的鲁棒性，纵向着舰点误差的变化范围却不是不大。

5 结论

本文基于L1自适应控制方法设计自动着舰控制律，并验证其鲁棒性和快速性。针对着舰最后阶段大气紊流和舰尾气流的影响，利用基于L1自适应方法设计的控制律的鲁棒性来克服其干扰。通过仿真来验证舰尾流的“随机性”对所设计的自动着舰控制律影响，仿真结果表明基于L1自适应控制的自动着舰控制律具有良好的鲁棒性，能够很好的克服舰尾流的影响。在此之后，进一步研究了舰尾流对纵向着舰点影响，首先，选取不同风速进行多次仿真，观察着舰点分布情况变化；然后，采用“单因素方差分析法”对着舰点分布情况进行分析，结果表明舰尾流对纵向着舰点具有显著性影响；最后，讨论了纵向着舰点随舰尾流风速变化趋势。最终也说明了纵向着舰点误差随舰尾流风速增加而增加。