风洞CTS试验六自由度机构控制方法研究
, ,
(中国空气动力研究与发展中心,四川 绵阳 621000)
0 引言
风洞捕获轨迹试验(captive trajectory simulation,CTS)主要用于模拟外挂物模型从飞机上投放/发射的分离过程,获取外挂物分离对母机安全性能影响评估数据[1]。捕获轨迹试验是由计算机控制的六自由度运动机构支撑外挂物,使外挂物保持给定位置和姿态,然后由外挂物内部的应变天平测量外挂物所受的气动载荷,根据测量的气动载荷求解外挂物运动方程,得到外挂物在下一时刻的位置和姿态,控制六自由度运动机构到达相应的位置和姿态,再根据气动载荷获得下一时刻的位置和姿态,如此往复的测量和计算,逐点获得外挂物运动轨迹[2]。因此,捕获轨迹试验的核心是六自由度运动机构的设计和控制[3]。六自由度运动机构由3个线位移和3个角位移组成,从结构上可分为并联机构和串联机构,结构形式由安装空间和控制的复杂度决定[4]。
本文分析了一种串联结构的六自由度运动机构位置关系和速度关系,结合机构特点,对其控制方法进行研究。
1 系统总体方案
六自由度运动机构可以在风洞试验段内实现前后(X)、上下(Y)、左右(Z)3个方向的线位移运动和俯仰(α)、偏航(β)、滚转(γ)3个方向的角位移运动试验装置。能够在计算机控制下实现给定速度控制和精确定位控制。
根据风洞结构和试验要求,该六自由度试验装置的总体结构如图1所示。

图1 六自由度装置总体结构
角位移部件实现3个角度变化,通常称为三转角头,下方的支撑平台实现3个位移变化,称为移测架。该装置采用串联结构,之下而上以次为Z向、Y向、X向、偏航β、俯仰α、滚转γ。Z向、Y向、X向机构采用丝杠螺母传动,将电机角位移转换为线位移。偏航β、俯仰α采用电动缸串联布置的轴叉式结构,由电动缸驱动角度旋转机构沿旋转轴旋转,以实现角度的偏转,角度编码器布置在旋转轴上,测量的角度即为机构的实际角度。滚转γ机构由直流伺服电机搭配谐波齿轮减速器驱动模型支杆实现转动,环形角度编码器布置在γ机构外圈,测量的角度即为机构的实际滚转角。三转角头机构如图2所示。该种结构的优点是装置外形尺寸小,传动间隙小,3个角度运动相互独立,无运动耦合[5]。
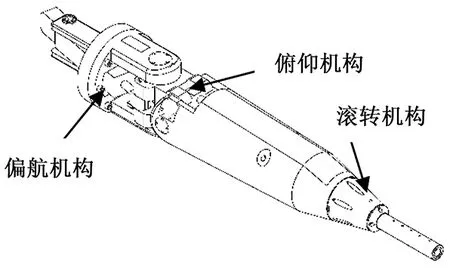
图2 三转角头结构
2 运动学分析
该六自由度机构3个线位移均为线性传动结构,通过直接控制电机的转角,经由丝杠传动机构将角位移转换为线位移,实现位移的控制。偏航β、俯仰α不是通过电机直接驱动的,而是通过控制电动缸的位移,经由电动缸螺母推动转轴旋转,间接实现角度变化,因此必须分析电动缸位移与角度的关系,通过角度计算电动缸位移,再控制电动缸位移变化,实现角度控制。
2.1 运动学建模
由于偏航β、俯仰α传动结构原理相同,下面以俯仰α为例分析电动缸位移和角度传动关系。迎角机构简化后,其几何关系示意图如图3所示,实线表示迎角为零位时各部分的位置,虚线为电动缸伸长移动s距离迎角转动α后的位置,规定电动缸伸长方向为正。
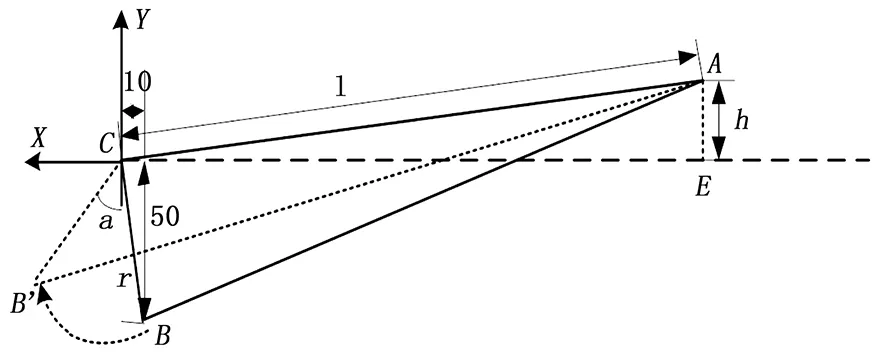
图3 俯仰机构原理
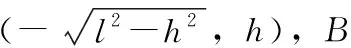
(1)
其中:h为固定点A到中心线的距离,l为旋转中心到固定连接端的距离,r为角度旋转半径,h=12 mm、l=325.22 mm、r=50.99 mm。当俯仰装置旋转α角度后,B移动到B′,B′的坐标值为(r·sin(α-arcsin(10/50)),r·cos(α-arcsin(10/50))),A、B′之间的距离为旋转α角度后电动缸的长度,可得:
(2)
电动缸长度的变化量为:
Δs(t)=AB′-AB
(3)
将机构参数带入式(1)~(3)可得电动缸变化量与俯仰角α的关系式为:
321.0327
(4)
电动缸变化量Δs(t)与俯仰角α的关系如图4所示。
将式(4)两边求导可得角速度和丝杠速度关系:
(5)
取角速度为4°/s时,电动缸速度和角度的关系如图5所示。
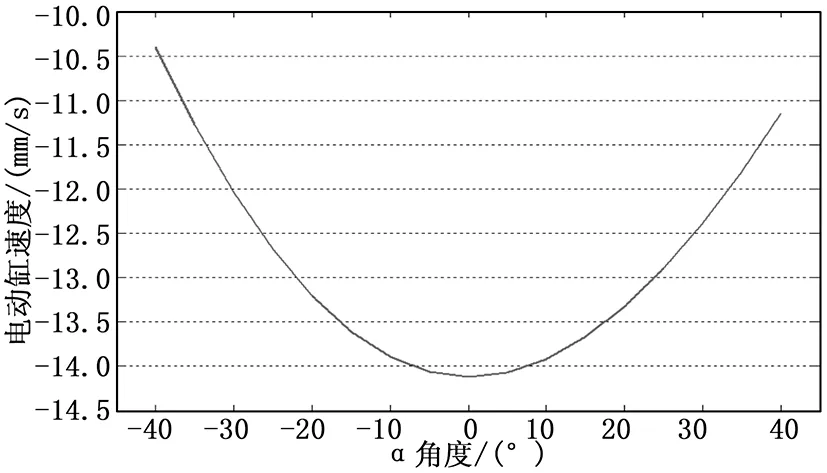
图5 电动缸速度与俯仰角α的关系
由角度和电动缸变化量之间的关系可知,两者之间的关系是一个非线性结构,电动缸的速度随着角度的变化而变化。为此,在进行角度控制时,需根据角度位置和角度速度来确定电动缸的位移和速度,且当角度的位置和速度变化后,对电动缸的速度和位移也应进行调整,以保证角速度不变。
2.2 运动关系分析
根据装置的结构,设定三自由度转角头的偏航关节处为基点O,俯仰关节处为中继点A,滚转关节处为中继点B,采用Z型支杆时模型中心基点为C,绘制传动原理图,见图6。
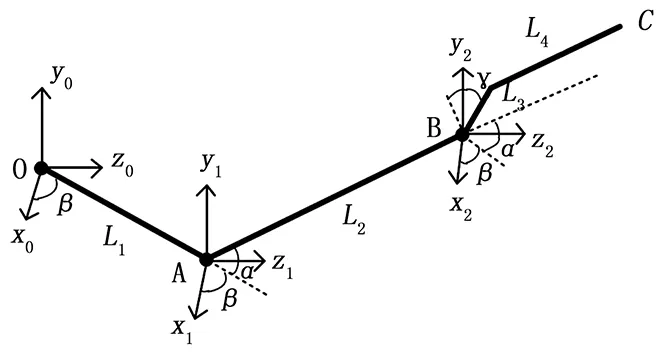
图6 角度与线位移的传动原理
根据三自由度转角头装置的传动原理图,建立该装置的动力学方程,得到俯仰关节处A点、滚转关节处B点和模型中心点C的位置方程:
A:(l1cosβ,0,l1sinβ)
(6)
(7)
C:(l1cosβ+(l2+l4)cosαcosβ+l3sinβsinγ-l3sinαcosβcosγ-
l1-l2-l4,(l2+l4)cosβsinα+l3cosαcosγ-l3,l1sinβ+
(l2+l4)cosαsinβ-l3sinαsinβcosγ-l3cosβsinγ)
(8)
从C点的坐标可知,当模型的姿态角发生变化时,模型的位置也发生了变化,而在试验中,只变化模型姿态角时模型位置应保持不变,因此在模型姿态角变化时,线位移必须进行补偿,保证模型中心位置不发生变化,线位移的补偿量为角度变化后模型中心坐标值取反。对式(8)求导,可得补偿速度为:
[l3cosβsinγ+l3sinαsinβcosγ-(l2+l4)cosαsinβ-l1sinβ]
(9)
(10)
[(l2+l4)cosαcosβ+l1cosβ-l3sinαcosβcosγ+l3sinβsinγ]
(11)
在运动过程中要保持模型位置不变,线位移的运动速度应随着角度的变化而变化。通过以上分析可知,偏航β、俯仰α、X、Y、Z的控制过程可分为两个阶段,一是运动过程中为速度控制,二是接近目标点时为定位控制。
3 控制方法研究
3.1 偏航β、俯仰α匀速控制方法
由传动原理可知,偏航β、俯仰α是控制电动缸位移来间接实现角度控制的,且两者之间的关系是非线性的。为了实现角度的匀速运动,将角度假想为一个虚拟旋转轴[6],令虚拟轴按照匀速速度曲线运行,根据角度的给定速度按照式(5)计算电动缸位移的运行速度,根据角度的给定目标值按照式(4)计算电动缸位移,控制电动缸按照该速度运行就可实现迎角的匀速运动,并在接近目标点时,按照电动缸位移进行定位控制。
为了保证机构运行平稳,可将运动过程分为3个阶段,既加速阶段、匀速阶段、减速阶段。按照加减速阶段的速度曲线又可分为线性加减速和非线性加减速,典型的速度曲线有梯形和S形[7]。
本文采用梯形加减速曲线作为角度运动过程,如图7(a)所示。设加速度和减速度均为a,匀速速度为Vm,运动距离为S,当前位置为S(t),当前时间为t,当前速度V。
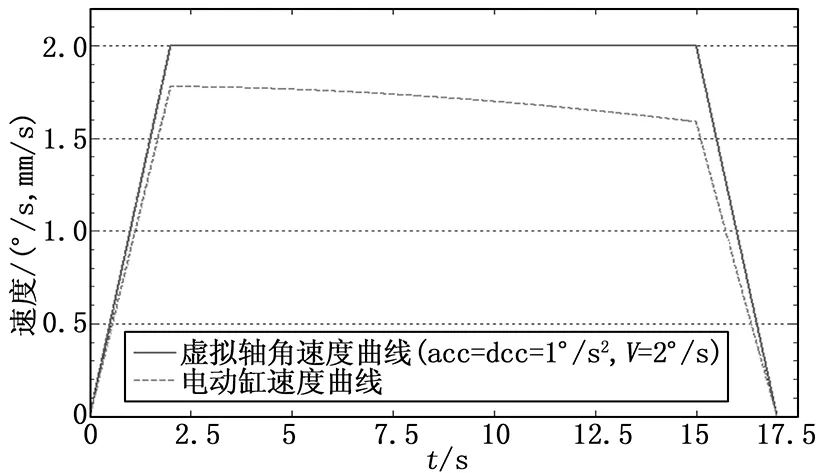
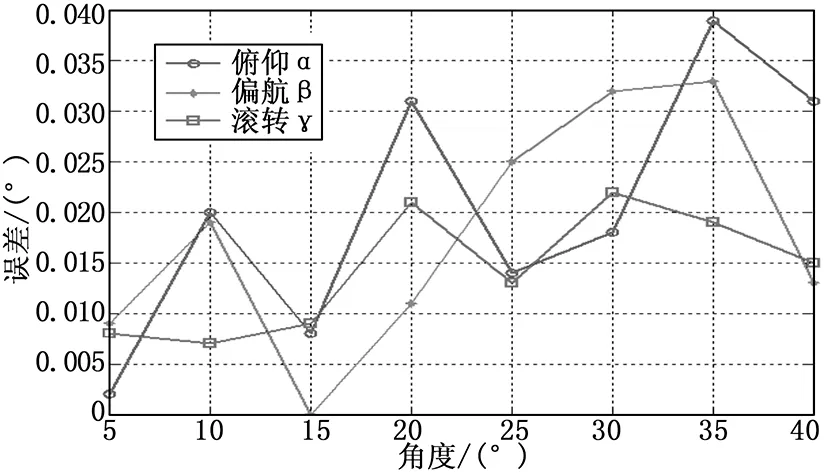
当运动距离S 图7 速度曲线 当S(t)≤S/2时为加速过程,V=at; 当运动距离S>Vm2/a时,速度曲线为标准的梯形曲线。 当S(t) 当Vm2/2a≤S(t) 当S-Vm2/2a≤S(t)≤S时为减速过程,V=Vm-a(t-S/V)。 根据以上分析,已知给定加减速度、最大速度、运动距离,就可计算出每时刻的运动速度,按照角度和电动缸的速度关系函数就可计算出电动缸的运行速度,按照采样间隔不断的刷新当前速度,即可实现角度的匀速运动。 根据角度速度曲线计算电动缸速度曲线如图8所示。 图8 虚拟轴和电动缸速度曲线 将角度匀速控制问题转化为电动缸跟随角度的随动控制问题。控制流程如图9所示。 图9 角度控制流程 控制的具体过程如下: 1)根据角度给定值和当前值计算角度运行距离; 2)根据角度位置、给定加减速度、匀速速度,计算当前角度瞬时速度。 3)根据角度瞬时速度,按照式(5)计算出电动缸当前位置的瞬时速度; 4)根据计算出的电动缸瞬时速度,重置电动缸控制速度; 5)读取角度反馈值,与给定值比较,判断是否到达目标值; 6)不断重复2)~5),直至达到角度最终目标值,结束本次控制过程。 在捕获轨迹试验过程中要求对模型姿态和位置同时控制,既有角度控制又有位置控制,为了真实模拟模型运动轨迹,6个自由度需要联动控制。从各轴的位置关系分析可知,各自由度之间相互独立,为了保证模型在运动过程中处于运动轨迹上,在角度变化时,模型位置要同时运动,且位置要补偿角度变化造成的位置偏差。此时的位置运动距离有两部分组成,一部分是位置目标值,另一部分是位置补偿值,可用下式表示: S距离=S目标+S补偿 (12) 其中:S距离为线位移运动距离,是线位移的控制量,S目标为模型位置坐标给定值,且按照匀速运动,S补偿为线位移的补偿量,由式(8)确定,随着角度的变化而变化,且运行速度也和角速度、角度值有关。 线位移的运行速度可表示为: V控制=V给定+V补偿 (13) 其中:V控制为线位移的控制速度,V给定为模型位置运动速度,V补偿为线位移的补偿速度,随着角度的变化而变化,和角速度、角度值有关,由式(9)~(11)确定。 六轴联动控制流程如图10所示。 图10 六轴联动控制流程 控制的具体过程如下: 1)获取模型位置和姿态运动目标值; 2)获取模型姿态当前值,用于计算模型位置的补偿量和补偿速度; 3)按照式(8)计算位置补偿量,按照式(12)计算位置运动距离; 4)根据α、β运动距离,按照梯形速度曲线计算当前角度速度,根据式(5)计算电动缸运行速度; 5)根据式(9)~(11)、(13)计算线位移的补偿速度和线位控制速度; 6)向各轴控制器发送速度控制指令,控制各轴按照给定速度指令运动; 7)控制周期未结束,则继续按照当前速度运动,控制周期结束,判断各轴位置是否到位,若未到位,则获取当前线位移和角位移当前值; 8)不断重复4)~7),直至达到位置和角度最终目标值,结束本次运动过程。 控制系统主要由主控计算机、运动控制系统、伺服驱动系统、安全保护装置等组成。系统采用“运动控制计算机+网络型运动控制器”的控制方式,两者之间采用工业以太网进行通讯,运动控制器控制指令采用脉冲方向信号,系统结构如图11所示。3个线位移采用交流伺服电机驱动的丝杠螺母机构+编码器反馈的半闭环控制结构实现。角位移采用双闭环控制,电机编码器反馈运动速度和电动缸位移至驱动器,构成速度环,角位移采用角度编码器,直接测量角度值,反馈至计算机构成角度闭环控制[8-10]。以上位运动控制计算机作为控制中心,实现速度计算、角度闭环控制、位置设定和显示、回零控制等功能。控制器实现使能控制、抱闸控制、限位等安全保护功能。 图11 控制系统总体结构 伺服系统选用以色列 Elmo公司的紧凑型和高智能直流伺服驱动器,角位移选用MAXON公司RE40系列直流有刷伺服电机驱动,线位移选用三菱交流伺服电机驱动。 控制器选用COMIZOA 网络型运动控制器,该控制器为模块化设计,可构成基于TCP/IP的分布式控制系统。以DSP 为核心,系统集成度高、接口简单、开放性好,能实现位置控制,多轴同步等。 控制软件是基于PC机运行的上位机控制软件,采用LabWindows/CVI开发环境,通过以太网通讯访问COMIZOA运动控制器,协调三转角系统、线位移系统的运动。同时可与风洞测控处系统试验管理机进行通信,接受试验管理机的指令,以实现整个风洞试验过程的自动化。系统具有单轴点对点、多轴联动等多种位置或速度运动模式,协调控制六自由度完成试验运行流程。 为了检验上述控制方法的控制效果,采用高精度倾斜仪(精度为1″)对偏航β、俯仰α角度轴的实际运行角度进行测量,并与名义角进行比较,考核其角度定位精度。控制误差如图12所示。 图12 角度控制误差 控制系统按照角度匀速控制方法,控制角度到目标位置,然后读取倾斜仪测量读数。结果表明,俯仰α角度控制最大误差为0.039°,偏航β角度控制最大误差为0.033°,且两者控制误差都随着角度的增大而增大的趋势,这可能是由于机构安装误差或机构变形所致。从整个机构运动范围而言,所有角度控制精度都达到或超过了试验要求指标(0.05°),能够满足试验要求。 本文针对风洞CTS试验六自由度机构,通过分析偏航β、俯仰α轴的传动关系,根据非线性传动关系的特点采用了基于虚拟轴的跟随控制,实现了角度的匀速控制。为了满足试验要求,定量分析了角度与线位移的运动关系,在此基础上,采用速度实时补偿的速度控制方法实现了6个自由度联动控制。采用高性能控制器和驱动器构成伺服控制系统,采用LabWindows/CVI开发环境实现了角度匀速控制和六轴联动控制算法。实验验证结果表明,角度控制精度都达到或超过了设计指标,能够满足试验要求。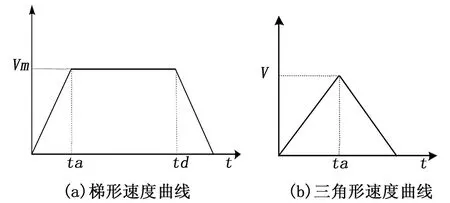
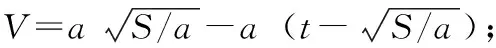
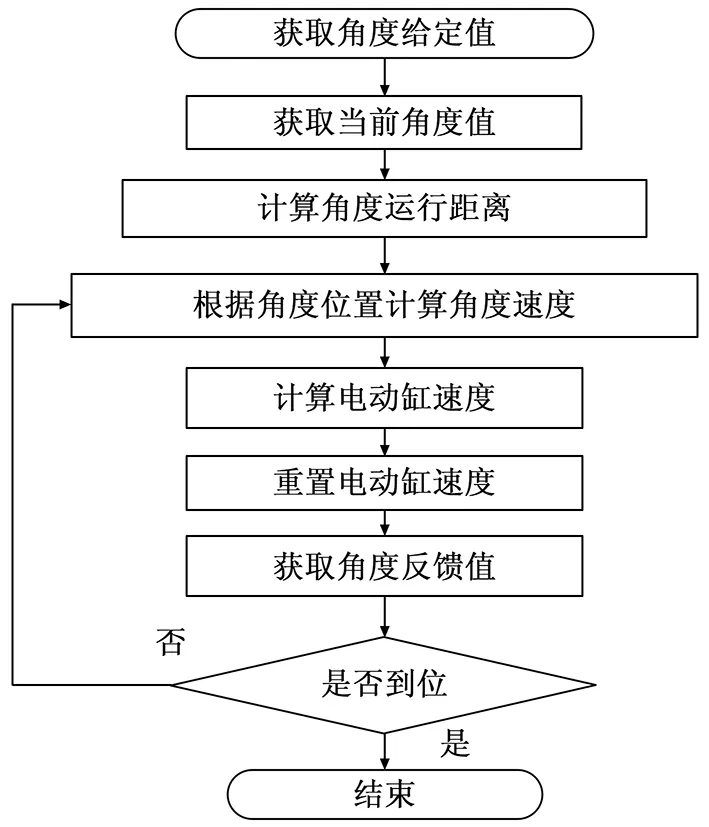
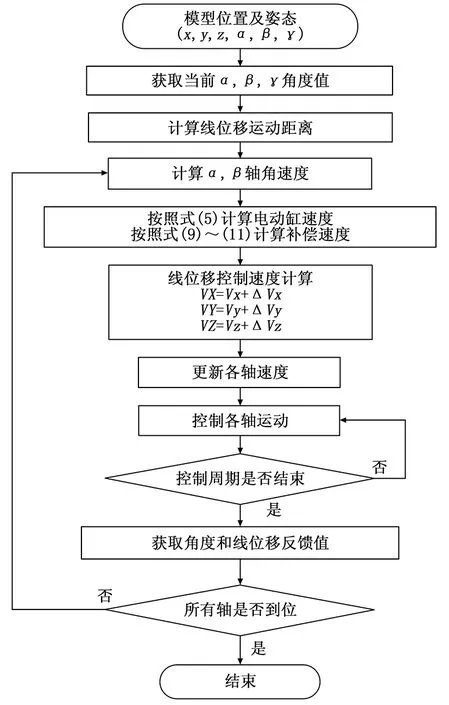
3.2 六自由度联动控制方法
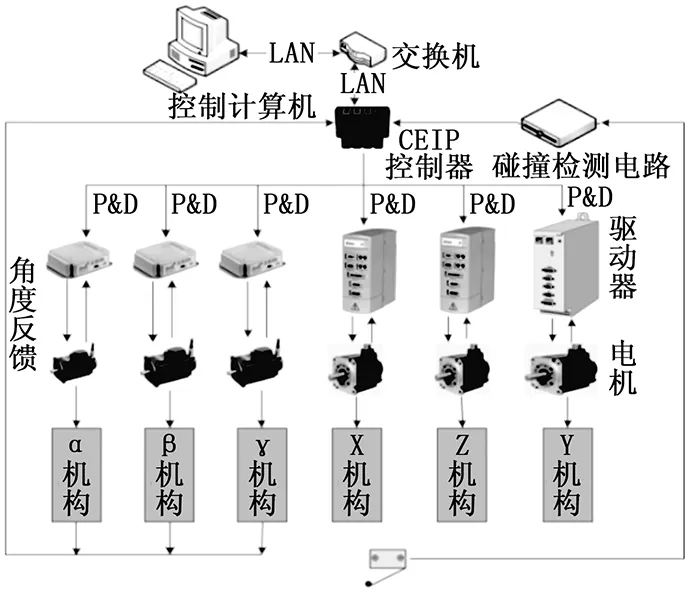
4 控制系统实现
5 实验验证
6 结论

