Measurement and prediction of cavitating flow-induced vibrations *

Qin Wu （吴钦）, Chang-chang Wang （王畅畅）, Biao Huang （黄彪）, Guo-yu Wang （王国玉）,Shu-liang Cao （曹树良）

1. School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China

2. Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, China

Abstract: The objective of this paper is to investigate the unsteady cavitation behaviors and the corresponding cavitating flow-induced vibrations. Results are presented for the modified NACA66 hydrofoils made of stainless steel and POM Polyacetate respectively at Re = 6.0× 105 for various cavitation regimes. The high-speed camera and the single point laser Doppler vibrometer (LDV) are used to observe the transient cavitating flow patterns and measure the vibration velocities. The results showed that the vibration amplitude increases dramatically for the cloud cavitation due to the development of large-scale cloud cavity. The main flow-induced frequencies,which are in accordance with the cavity shedding frequency, decrease with the decrease of the cavitation number. As for the effect of the hydroelastic response on the vibration behavior, the lift coefficient for the POM Polyacetate hydrofoil fluctuates more significantly with a larger mean value than that for the stainless steel hydrofoil. Compared with the vaporous cavity along the suction side of the stainless steel hydrofoil, the cavity for POM Polyacetate hydrofoil appears to be fragmentized. The main vibration frequencies for the POM Polyacetate hydrofoil are larger than that for the stainless steel hydrofoil, with the chaotic hydroelastic response with high frequency.

Key words: Cavitating flow, flow-induced vibrations, hydrofoil

Introduction

Cavitation involves complex interaction between phase-change and vortex structures and it is of significant importance for marine structural design (e.g.,propulsive systems)[1-7]. It is well known that the unsteady breakdown and shedding of the cavities will induce strong transient loads and lead to further hydrodynamic instabilities, even structure failures.Hence, it is necessary to understand the influence of unsteady cavitation on the flow-induced vibrations,which in turn affects the unsteady cavitating flow behaviors.

Flow-induced vibration problem has been one of the major issues in a wide range of fields, such as fluid mechanics, structural mechanics, computational fluid dynamics and acoustics for a long time[8-12]. So et al.[13]investigated the structural dynamics and wake flow in the free vibration of an elastic cylinder in a cross flow, using a laser vibrometer to assess the bending displacements and a laser Doppler anemometer to measure the velocities in the wake. They found that the cylinder vibrations enhanced the turbulent mixing and increased the turbulent intensities.Based on the general vibration characteristics, many effects, such as material properties and hydrofoil trailing edge shapes, on the fluid-induced vibration have also been discussed in Zhang et al.[14], Zobeiri et al.[15]and Yao et al.[16].

In addition to the above works that focused on fully wetted flow-induced vibration, flow induced vibration in cavitating flows were experimentally studied by Brennen et al.[17], Kawakami et al.[18]and Arndt[19]. Amromin and Kovinskaya[20]analyzed the vibration of an elastic hydrofoil with an attached cavity in periodically perturbed flow, where a beam equation was used to describe the hydrofoil vibration.The results showed that the structural vibration increased significantly due to the cavitation. The high-frequency band was attributed to the hydrofoil resonance with the cavity adding a certain damping and the low-frequency band was corresponding to the cavity volume fluctuations. Ausoni et al.[21]conducted the experimental studies to investigate the effects of cavitation and fluid-structures interaction on vortex generation mechanism. They found that the vortexinduced vibration level significantly increased at cavitation onset and the transverse velocity at the hydrofoil trailing edge increased the vortex strength.De La Torre et al.[22]conducted a series of experiments to investigate the influence of the sheet cavitation and supercavitation on the added mass effects experienced by a modified NACA0009 hydrofoil. The results showed that the added mass decreases when cavitation appears because of the increased cavity length.

Although the fully wetted flow-induced vibration and the phenomenon of cavitation have been widely studied, further investigation of the flow induced vibration under different cavitation regimes and with different structural material properties are still needed.The objective of this work is to shed light on the unsteady cavitating flow and corresponding vibration characteristics, as well as the effect of the hydroelastic response on the flow-induced vibration.

1. Experimental setup

Experimental studies are conducted in a closedloop cavitation tunnel at Beijing Institute of Technology[23], which is shown in Fig. 1. The test section is 0.70 m long and has a rectangular section with width of 0.07 m and height of 0.19 m. An axial flow pump,which is applied to drive the flow in the tunnel, is located about 5 m below the test section. A tank with volume of 5m3is placed upstream of the test section to separate the undesired free stream bubbles in the flow, and the water in the reservoir has been kept still for a period of time before the experiment to ensure the completely precipitate of the sediment and gas.The vacuum pump is connected to the top of the tank and regulated by the pressure controller according to the working pressure. Between the tank and the test section, a corner vane and a straightening vane are set to reduce the flow turbulence level. The upstream pressure and the flow velocity are measured by the vacuometer (with the uncertainty 0.25% of the maximum range) and the electromagnetic flowmeter(with the uncertainty 0.5% of the maximum range)respectively. The blockage ratio based on the hydrofoil maximum thickness, 9 mm, is 4.7%.

Figure 2 shows the schematic of the experimental setup. Experimental results are presented for the modified NACA66 hydrofoil, which has a uniform cross-section of shape with chord length c = 0.075 m ,the span=0.069 m and a maximum thickness-tochord ratio of 12%. Figure 2(a) shows the illustration of the test section, and the hydrofoil is placed with an incidence angle of 8°. A high-speed camera with a sampling frequency of 2 500 fps has been used to capture the cavity patterns from the front and top view.A single point laser Doppler vibrometer (LDV) with a sample frequency of 22 kHz has been applied to measure the structural vibration velocity from the bottom of the hydrofoil, with the measure point located at the mid-plan of the hydrofoil and also near the rear end of the hydrofoil, as shown in Fig. 2. Then the vibration velocity signal can be fed into digital inputs of a data acquisition system, followed by a three-level 1-D wavelet analysis using the Haar wavelet to de-noise the signal. In the present study,the hydrofoils made of stainless steel (SS) and POM Polyacetate respectively are compared, whose specific properties are given in Table 1 and the mass ratio is defined as

Fig. 1 Schematic of the cavitation tunnel

Fig. 2 (Color online) Illustration of the test section and measure point

Table 1 The specific properties of the materials

2. Numerical methods

2.1 Governing equations

The unsteady Reynolds average Navier-Stokes(URANS) equations are used due to its balance between the accuracy and the computational cost.

where ρ is the fluid density, u is the velocity, p is the pressure, μ is the laminar viscosity, μtis the turbulent viscosity. The subscripts m, l, v are representing the mixture fluid, liquid and vapor, i,denote the directions of the Cartesian coordinates.

The URANS equation is solved using the k-ω SST turbulence model[24], which applies the k-ε model away from the wall and the k-ω model near the wall. To better consider the local compressibility effect of the multiphase mixture on the turbulence model, the turbulent viscosity is revised by replacingμtwith μmodt[25]:

where =3n is chosen and the validation studies can be referred to Huang et al.[26].

Fig. 3 (Color online) Typical cavitation patterns and vibration characteristics for different cavitation regimes

2.2 Cavitation model

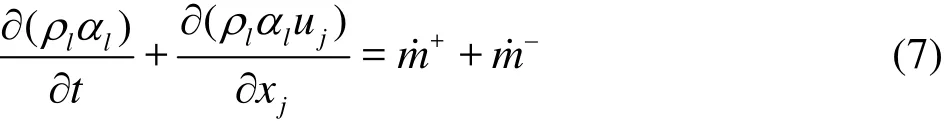
The cavitation flow is governed by the mass transfer equation for the conservation of liquid/vapor mass fraction, which can be defined as In this work, the Zwart cavitation model[27]is used, which is derived from Rayleigh-Plesset equation and provides the rate equation controlling vapor generation and condensation. The evaporation and condensation rates are defined as:

where pvis the saturated vapor pressure, Cdestandare the constant rate of vapor generation and re-conversion,nucα is the nuclei volume fraction,is the bubble diameter.

2.3 Solid model

To investigate the hydroelastic characteristics of the hydrofoil, it is assumed as a chord-wise rigid, two degree of freedom model. The bending and twisting deformation of the hydrofoil are considered in this work, which are defined as the plunging and pitching motion of the tip section. The governing equation of the 2-DOF system motion without external excitation forces can be written as

where m is the structural mass,is the static imbalance and lθis the inertia moment. Chand Cθare the structural damping for the bending and torsion motions,andare the structural stiffness for the bending and torsion motions.andare the bending/twisting acceleration,velocity and displacement. L and M are the lift(be positive along the Y-axis) and moment (be positive as the counter-clockwise direction) acting on the hydrofoil, which are computed by the fluid solver.

Fig. 4 (Color online) Measured and predicted vibration amplitudes for the stainless steel hydrofoil and POM Polyacetate hydrofoil

2.4 Fluid structure interaction model

To better account for the effects of fluid inertial,damping and restoring forces and avoid the numerical instability issues associated with artificial added mass effects, the hybrid coupled fluid structure interaction model[28]combined with Theodorsen assumption[29]is applied in the present work

Fig. 5 Spectrogram of the vibration velocities for different cavitation regimes

3. Results and discussions

3.1 Global cavity shapes and induced vibrations

Figure 3 shows the typical cavity shapes of the POM hydrofoil for different cavitation regimes and corresponding vibration velocities (Vvel) and amplitudes (Vamp) . In which, the vibration amplitude is calculated via the integral of the vibration velocity. With decreasing of the cavitation number, the cavitating flows display several patterns: incipient cavitationand cloud cavitation (σ = 0.8). The corresponding vibration velocity and amplitude vary with time, and the maximum vibration velocity and amplitude is relative small for the incipient cavitation (σ = 2.0), as shown in Figs.3(b), 3(c). With decreasing of the cavitation number,the cavity length increases, as shown in Fig. 3(a), the unsteady rear portion of the sheet cavity leads to the rising of the vibration amplitude for the sheet cavitation (σ=1.2). Further lowering the cavitation number, the large-scale cloud cavity begins to form and the corresponding vibration amplitude increases dramati- cally for the cloud cavitation (σ = 0.8).

Fig. 6 (Color online) Predicted lift coefficients for the stainless steel hydrofoil and POM Polyacetate hydrofoil

To better investigate the vibration characteristics of hydrofoil under different cavitation regimes, Fig. 4 compares the experimentally measured and numerically predicted structural vibration amplitudes for the POM Polyacetate hydrofoils during several cavitation development periods. Good agreement can be obtained between the experimental and numerical results, except for the incipient cavitation (σ = 2.0).This is because the vibration amplitude for the incipient cavitation is too small that the measured vibration amplitude is significantly affected by the vibration environment, resulting the measured vibration amplitude is a superposition of many different vibration modals. As for the sheet cavitation (σ =1.2) and the cloud cavitation (σ = 0.8), the numerical results are able to well present the structural vibration characteristics. It can be found that the cavitation plays an important role on the vibration of the hydrofoil, so the vibration amplitude varies with time periodically, corresponding to the development and shedding of the sheet/cloud cavities.

Figure 5 shows the spectrogram of the vibration velocity, with the recording time of 0.5 s and 10 240 points, where the Complex Morlet Wavelets window function[31] is adopted during the post-processing. The main frequencies decrease with the decrease of the cavitation number, which are 165 Hz, 90 Hz and 18 Hz for the cases with σ = 2.0, 1.2 and 0.8. Combined with the observation of the transient cavity patterns, it is found that the main vibration frequencies are in accordance with the cavity shedding frequency, which means the cavity shedding process plays an important role in the vibration of hydrofoil.

3.2 The effect of hydroelastic response on the induced vibration

To investigate the effect of the hydroelastic response on the cavitating flows, Fig. 6 shows the evolution of the predicted lift coefficient for the stainless steel hydrofoil and POM Polyacetate hydrofoil. It can be found that the lift coefficients for both hydrofoils have periodic features, and because the vibration amplitudes are relatively small, the hydroelastic response of the POM Polyacetate hydrofoil have an effect on the lift coefficient within a reasonable extent. For the incipient cavitation ( =σ 2.0), as shown in Fig. 6(a), the lift coefficients fluctuate with the same phase, and the lift coefficient for the POM Polyacetate hydrofoil is a little larger than that for the stainless steel hydrofoil, with the fluctuating range of 3% and 1% respectively. While for the sheet cavitation (=1.2)σ, as shown in Fig.6(b), the lift coefficient fluctuates more significantly,with the mean lift coefficients for the POM Polyace-tate hydrofoil and the stainless steel hydrofoil are 0.92 and 0.89 respectively. This is due to the larger effective angle of attack for the POM Polyacetate hydrofoil caused by the twist deformation. Besides,when the lift coefficient reaches to the maximum value (seen the peaks of lift coefficient in Fig. 6(b)),that for the POM Polyacetate hydrofoil fluctuate with a high frequency and a small amplitude. As for the could cavitation (σ = 0.8), as shown in Fig. 6(c), the lift coefficient for the POM Polyacetate hydrofoil fluctuate much more significantly during the cavitation development process. This is because under transient hydrodynamic forces, the deformation of the POM Polyacetate hydrofoil is varying with the time,which corresponds to a more complex pattern of the transient hydrodynamic forces.

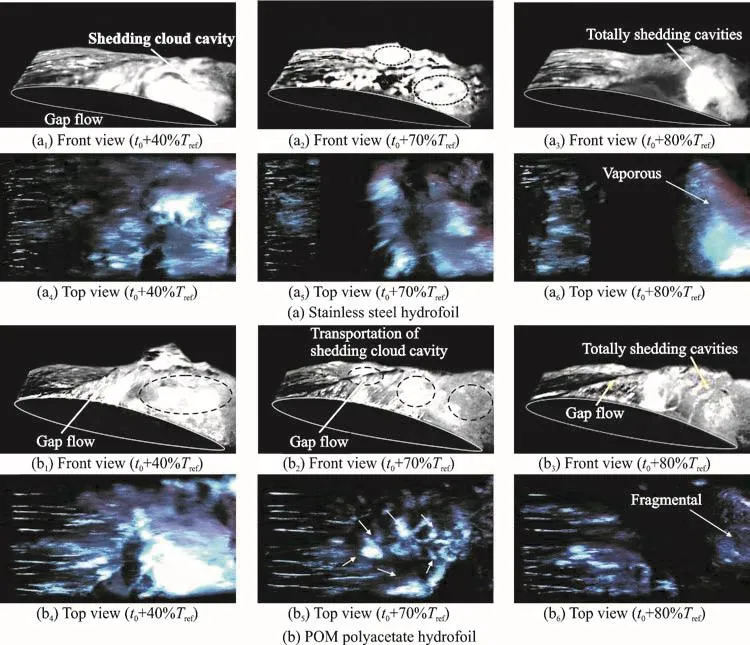
Fig. 7 (Color online) Observations of the cavitation patterns for stainless steel and POM Polyacetate hydrofoils

Since there is strong flow dynamic instabilities and significant structural vibrations in the cloud cavitation regime, Fig. 7 compares the cavity patterns for the stainless steel hydrofoil and POM Polyacetate hydrofoil at some typical moments during the cavity shedding process, to further investigate the transient cavitating flow which has a great effect on the vibration of the hydrofoil.large-scale cloud cavity breaks up with main cavity and sheds downstream. For the stainless steel hydrofoil, when the cloud cavity reaches to the trailing edge, the cloud cavity sheds as a whole and is transported with the main flow, as shown in Fig. 7(a).While due to larger effective angle of attack caused by the twist deformation of POM Polyacetate hydrofoil,the cloud cavity partially collapses with the vibration and breaks into several medium-scale cloud cavities,as shown in Fig. 7(b). Compared with the vaporous cavity attached on the suction side of the stainless steel hydrofoil, the cavity for POM Polyacetate hydrofoil is affected by the unsteady hydroelastic response and appears to be fragmentized.

Fig. 8 (Color online) The frequency spectrum of the vibration velocities for stainless steel and pom polyacetate hydrofoils

Figure 8 compares the frequency spectrums of measured vibration velocity for stainless steel and POM Polyacetate hydrofoils in cavitating flows. It can be observed that the main vibration frequency0f for both hydrofoils is about 18 Hz and 22 Hz respectively.The main vibration frequencies are in accordance to the main cavity shedding frequencywhich can be obtained from the observation of the cavity development shown in Fig. 7. In addition,compared to the results for stainless steel hydrofoil,the chaotic hydroelastic response with high frequency can be observed for POM Polyacetate hydrofoil. This is mainly attributed to the disturbance caused by the flow-induced flutter and deformation of the foil,corresponding to the more complex cavitation pattern shown in Fig. 7.

4. Conculsions

In this paper, the unsteady cavitating flow around a modified NACA66 hydrofoil and corresponding flow-induced vibration characteristics are studied. The primary findings include:

(1) The vibration magnitude of hydrofoil changes with different cavitation regimes: it keeps relative small for the inception cavition and sheet cavitation,increases dramatically for the cloud cavitation because of the increasing unsteadiness of large-scale cloud cavity. The main flow-induced frequencies are in accordance with the cavity shedding frequency, which decrease with the reduction of the cavitation number.

(2) The deformation of the POM Polyacetate hydrofoil results in a more complex pattern of the transient hydrodynamic forces and a more unstable cavity shedding behavior. The lift coefficient for the POM Polyacetate hydrofoil fluctuates more significantly with a larger mean value than that for the stainless steel hydrofoil. Compared with the vaporous cavity along the suction side of the stainless steel hydrofoil, the cavity for POM Polyacetate hydrofoil is affected by the unsteady hydroelastic response and appears to be fragmentized. And the main vibration frequencies for the POM Polyacetate hydrofoil is larger than that for the stainless steel hydrofoil, with the chaotic hydroelastic response with high frequency.

Regarding the future work, more additional experimental measurement of the hydrodynamic forces for different cavitating flow conditions will be conducted.Besides, according to some previous researches, there is very strong pressure fluctuation induced by the cavitation development[32-33], so in the future, the relation between the cavitation development, the pressure fluctuations and the flow-induced vibrations will be further investigated.

Acknowledgements

This work was supported by the National Postdoctoral Program for Innovative Talents (Grant No. BX201700126), the China Postdoctoral Science Foundation (Grant No. 2017M620043), and the Beijing Municipal Natural Science Foundation of China (Grant No. 3172029).