时间序列ARIMA与BP神经网络组合模型在CPI预测中的应用

孟毅



时间序列ARIMA与BP神经网络组合模型在CPI预测中的应用

孟毅

岭南师范学院商学院, 广东 湛江 524048

CPI是消费者在市场内进行消费和服务时所支付的价格随时间变化的平均指数。由于CPI对很多经济指标都有影响，它备受人们的关注。本文选取了ARIMA时间序列、BP神经网络和BP-ARIMA组合模型的三种方法对2009~2017年我国的CPI月度数据进行建模，并以此预测2017年度各月的CPI。结果表明，BP-ARIMA组合模型预测效果最优。

CPI; ARIMA时间序列; BP神经网络; BP-ARIMA组合模型

居民消费价格指数（CPI），是指消费者在市场内进行消费和服务时所支付的价格随时间变化的平均指数，可综合反映居民购买能力变动情况。它涵盖了上百种基本消费品和服务类别，通过统计和计算不同类别和子类别的商品和服务计算的子指标和分指标，结合一定的权重得到国家的居民消费价格指数总指标。消费价格指数的空间分类也很多种，不仅有各个省份统计计算的消费价格指数，也有城市居民农村居民的的消费价格指数。消费物价指数可以用来判断通货膨胀，也是有时被视为衡量政府经济政策有效性的指标。它向政府、企业和私人公民提供关于国家经济价格变化的信息，并以此作为制定经济决策的指南。此外国家会利用消费物价指数的趋势，协助制定财政和货币政策。

对于消费者来说，CPI也作为判断他们购买力的一个标准，而消费者的购买力衡量了一定量的货币在不同日期购买商品或者服务的价值的变化。因此，居民消费价格指数是仅次于人口的普查最受关注的国民经济统计指标。若是通过预测合理应用CPI指标，可以帮助国家和居民度过通货膨胀等特殊时段，制定相应的措施促进中国市场稳健地发展。

ARIMA时间序列简单易操作，它是目前最常被用于预测的方法，同样可以拿来预测CPI。在这一方面，国内已经有很学者进行了建模分析，郭晓峰[1]建立了ARIMA（12,1,20）模型，成功地预测了未来的CPI走势，并且得到了很好的结果。BP神经网络也是另一个被用来预测CPI的常用方法，郑艳伟,钱乐祥[2]等人使用归一化的方法对数据进行了预处理，选择神经网络的训练样本，利用神经网络的结构特性对广东省的CPI进行了建模并预测。刘海萍，王海涛[3]等人利用MATLAB软件建立了BP神经网络，并对山东省的物价消费指数进行了预测。

尽管使用时间序列分析和BP神经网络预测CPI的方法都很成熟，但是由于每个预测模型都有自己的特征和使用的局限性，反应的数据信息也存在一定区别，因此只使用一个模型难免会丢失信息。本文拟采用ARIMA模型和BP神经网络的组合模型对居民消费价格指数进行预测，并比较三种方法预测的准确性。

1 ARIMA模型和BP神经网络组合模型

在大多数情况下，任何一个单一模型都会存在一定的不可避免的缺陷或不可靠性，而组合模型则可以把单个模型的缺点尽可以的缩小到最小化，建立成最优模型。组合模型的研究重点集中于对两个到数个模型的预测结果进行组合，基本的思想就是充分利用每个预测方法所包含的独立的信息，通过一些已知可靠的方法确定权重，对模型的结果进行组合。在本文中，组合模型的建立主要包含两个部分：权重的计算与模型可靠性的检验。

其中，权重的计算是建立组合模型最为关键的一点，也是最核心内容。确定权重的方法有很多，目前使用率较高的权重确定方法有以下几种：

（1）等权重法：这种方法很容易理解，顾名思义，这种方法是通过给需要组合的数个模型结果以相同的权重。这种方法最简单，但是可靠性最低。因为除了将权重平均并没有其他的依据。

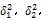
这里选取权重是为了让组合模型预测的方差最小，所以等式右侧对求导，并使之等于零可以得出：

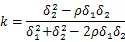
这种方法比第一种更为可靠，但必须满足两种预测模型预测的结果都是无偏的假设才可以使用，因此这个算权重的方法有一定的局限性。

2 居民消费价格指数预测实证分析

2.1 数据的选取

本文选取了2012年1月到2017年12月的月度中国物价消费指数作为研究对象，其中2012至2016年数据用于建立模型，由于2017年数据已知，可以用来计算误差及检验模型，数据来源为国家统计局网站。

2.2 ARIMA模型

2.2.1 平稳性检验 ARIMA模型估计的可靠性依赖于变量的平稳性。若非平稳，则进行差分，当进行到第次差分时序列平稳，则服从阶单整。所以，首先要对变量的时间数据序列进行ADF检验，以此判断变量进行的平稳性。

对CPI时间序列进行ADF单位根检验，其中-statistic值为-2.720681，尽管它小于0.1级别下的-statistic，但是大于0.05和0.01级别检验下的-statistic。表明在0.05和0.01的显著性水平下，都接受存在一个单位根的原假设，即序列非平稳。由于CPI序列具有非平稳性质，再对其进行一阶差分处理DCPI，由表1可知，一阶差分后序列平稳。

表 1 变量的ADF检验

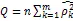
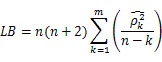
由表2可知当延迟6，8，12阶的时候，值都小于显著性水平0.05。也就是说，在显著性0.05的水平下，我们可以拒绝纯随机检验的原假设，即序列DCPI不具有纯随机性质。

表 2DCPI序列的相关性

Table 2 Correlation ofDCPI sequences

2.2.3 模型定阶对于模型ARIMA（，，），一共需要确定三个参数，，，。其中为差分运算的次数，由前文已知值为1。另外两个指标，由偏自相关系数判断，应该由自相关系数做出判断。由表2我们已经得到了差分序列DCPI的相关图，可以看到无论是自相关还是偏自相关系数都并不满足在某个阶数后，在0附近变动的性质。也就是说它们这两个量都是拖尾的，证明这组数据适合用ARIMA模型来建模。经过初步判断，认为可取1，12，可取1，2，11，12。

通过对相关系数的判断，已经可以估计出几个适用的模型。但为了选择出最优模型，还需要通过AIC和SBC等信息准则对几个模型进行比较进行筛选。判断准则是AIC值应该相对来说最小，DW值最接近2，-squared，Adjusted R-squared最大，值小于0.05。通过几次模型建立与比较，最终确定最优模型为ARIMA(1,1,12)。如表3所示，构建的ARIMA模型为：

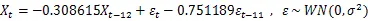
表 3 ARIMA(1,1,12)各项指标

2.2.4 模型检验判断一个模型显著与否的标准是看它所提取的数据信息是否充分，这里可以用白噪声检验判断残差是否还含有有效信息。假定残差序列为白噪声序列时，模型已经充分提取所需的数据信息，那么也就是说残差序列里面不再包含有效可利用的数据信息。对残差序列进行白噪声检验，在显著性水平为0.05的条件下，所有滞后期的Q统计量的值均大于0.05，这说明残差序列是白噪声序列。

2.2.5 模型预测先用ARIMA（1，1，12）模型采用静态预测的方法预测2012年到2016年的CPI值，从结果判断模型的优劣。由图1，CPI与CPIF(静态预测值)的走势基本上是相互符合的，也就是说模型ARIMA（1，1，12）的拟合度较好。接下来，可采取动态预测未知的2017年1月到2017年12月的居民物价消费数据。由图2，尽管所预测的CPIF与CPI2017的整体趋势变动都很接近，但是数值之间仍有差距。也就是说尽管表明了模型的准确性，但是预测的效果有待提高。

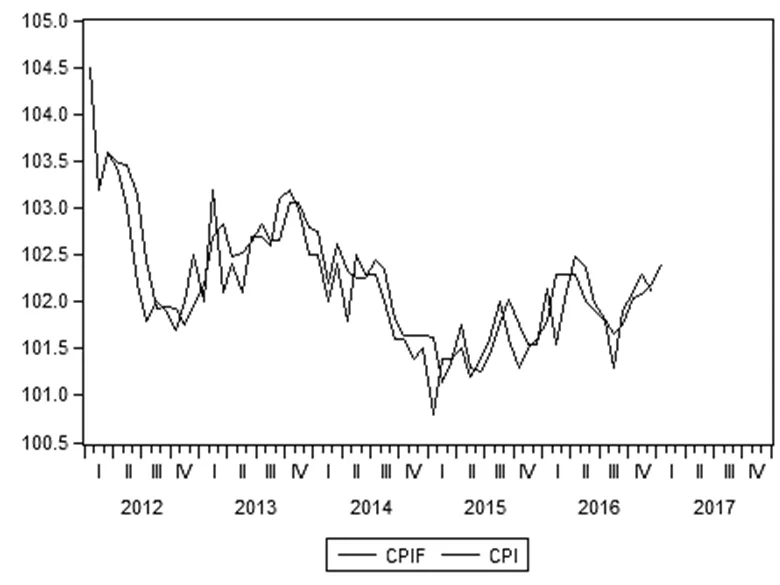
图 1 ARIMA（1,1,12）静态预测

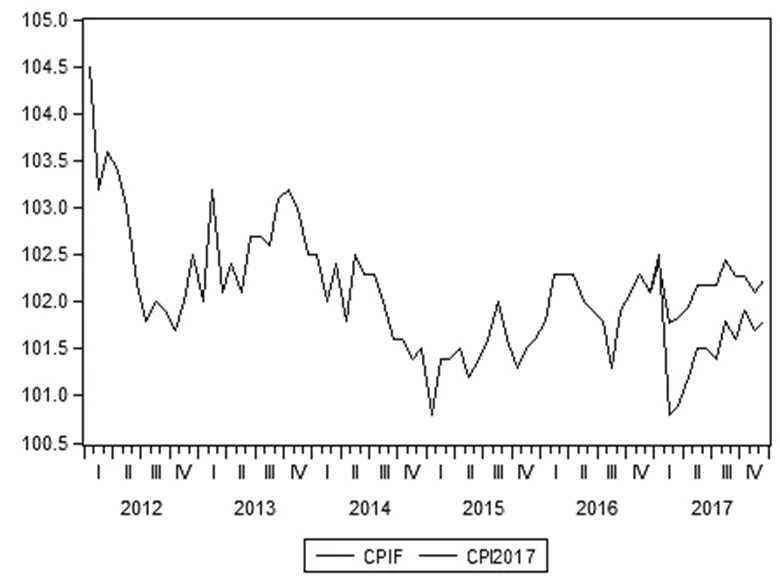
图 2 ARIMA（1,1,12）动态预测

2.3 BP神经网络模型

2.3.1 数据预处理首先，先对收集的数据进行划分。训练数据为2012至2016年的CPI数据，其中2016年的CPI为目标数据。测试数据则选取2013年至2016年的CPI数据，并得出预测的2017年的CPI值。

然后，需要对训练数据进行预处理，这里采用归一化的方法。应用训练数据确定的归一化的格式同样处理测试数据。当模型建立之后，采用翻转函数用逆归一化的方法，将预测的数据恢复成具有实际意义的数据，以便更好地观察和做下一步的检验。

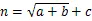
其中，是输入层的神经元个数，为隐层的神经元个数，为输出层的神经元个数。的取值从1到10，不断改变，逐个比较模型，选择的应该使得模型相对来说最准确。文中选取第一个经验公式，并且发现当神经元取8时，得到的模型MSE最小，为0.4326。因此确定隐层神经元个数为8。

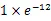
2.3.4 模型预测以及检验得到了合理可用的BP神经网络模型后，接下来对2017年1月至12月间的CPI进行预测，并且计算出相对误差(%)以便更好地判断模型，结果如表4。这里通过相对误差可知，预测出的2017年的CPI与真实值非常接近，模型预测效果良好。

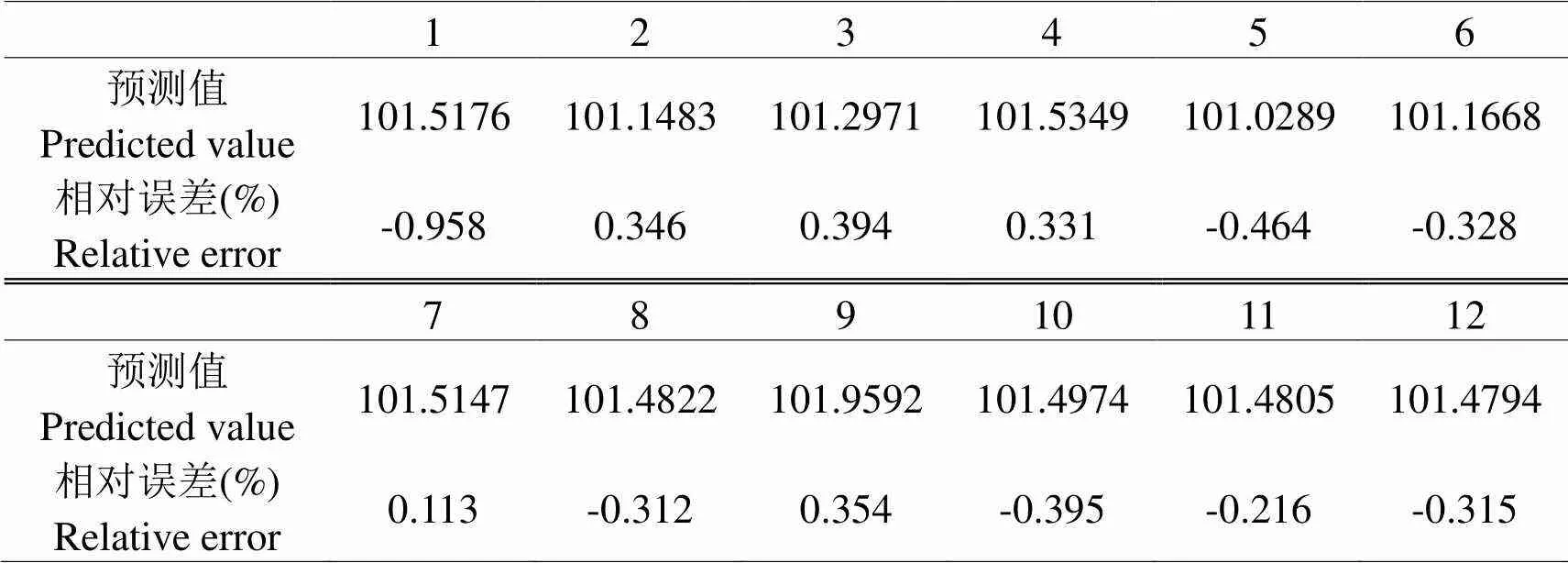
表4 BP神经网络模型预测值和相对误差

2.4 BP-ARIMA组合模型预测

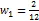
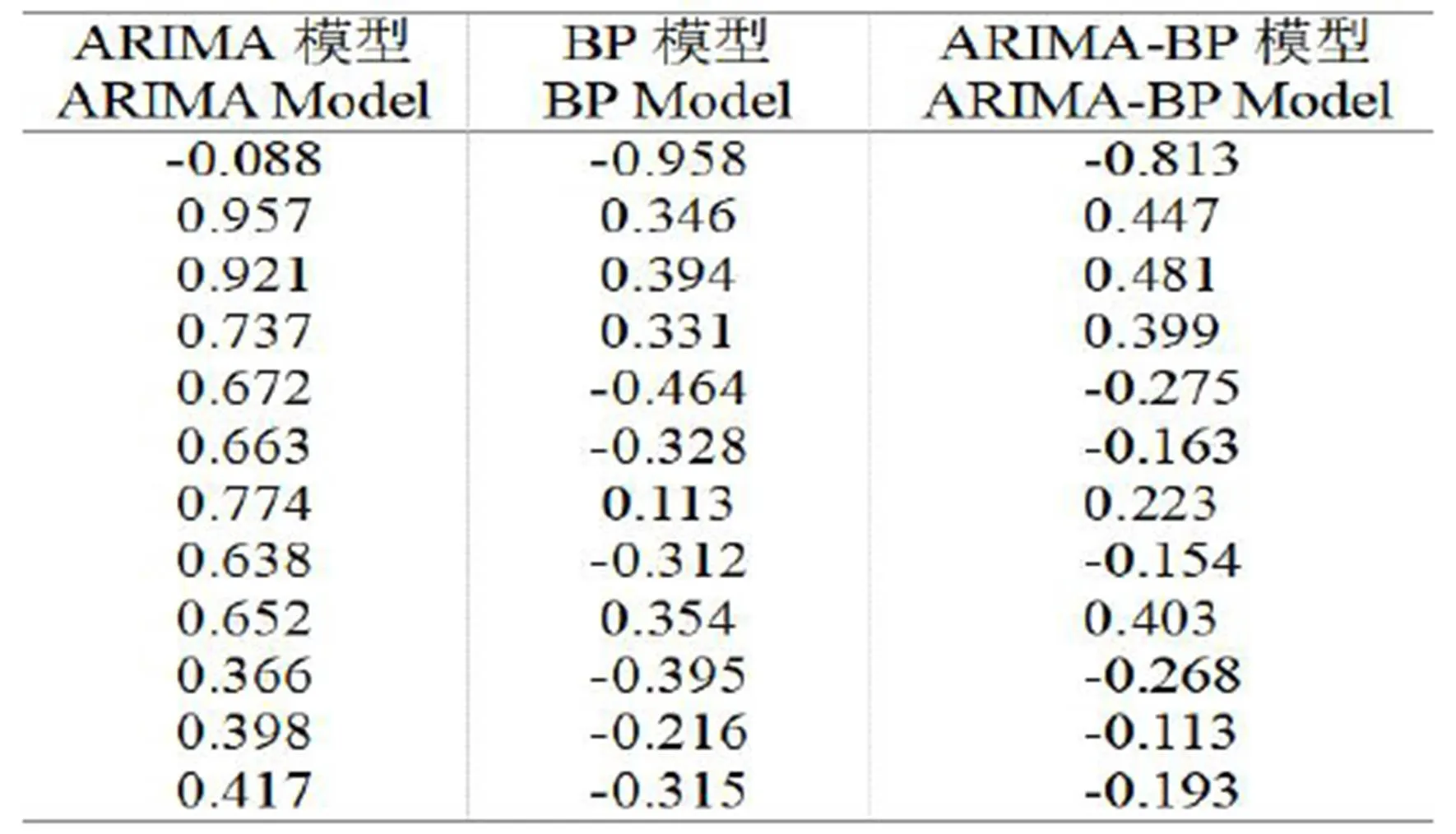
2.4.3 模型检验为了更好的检验组合模型预测效果，分别计算三个模型的相对误差。由表5比较三个模型的相对误差，可以发现组合模型ARIMA-BP相对误差比其他两个模型相对误差小的次数更多，并且组合模型在稳定性方面表现最好。综上，使用组合模型ARIMA-BP预测CPI结果是有效的，并且比单独使用ARIMA或BP模型的效果更好。

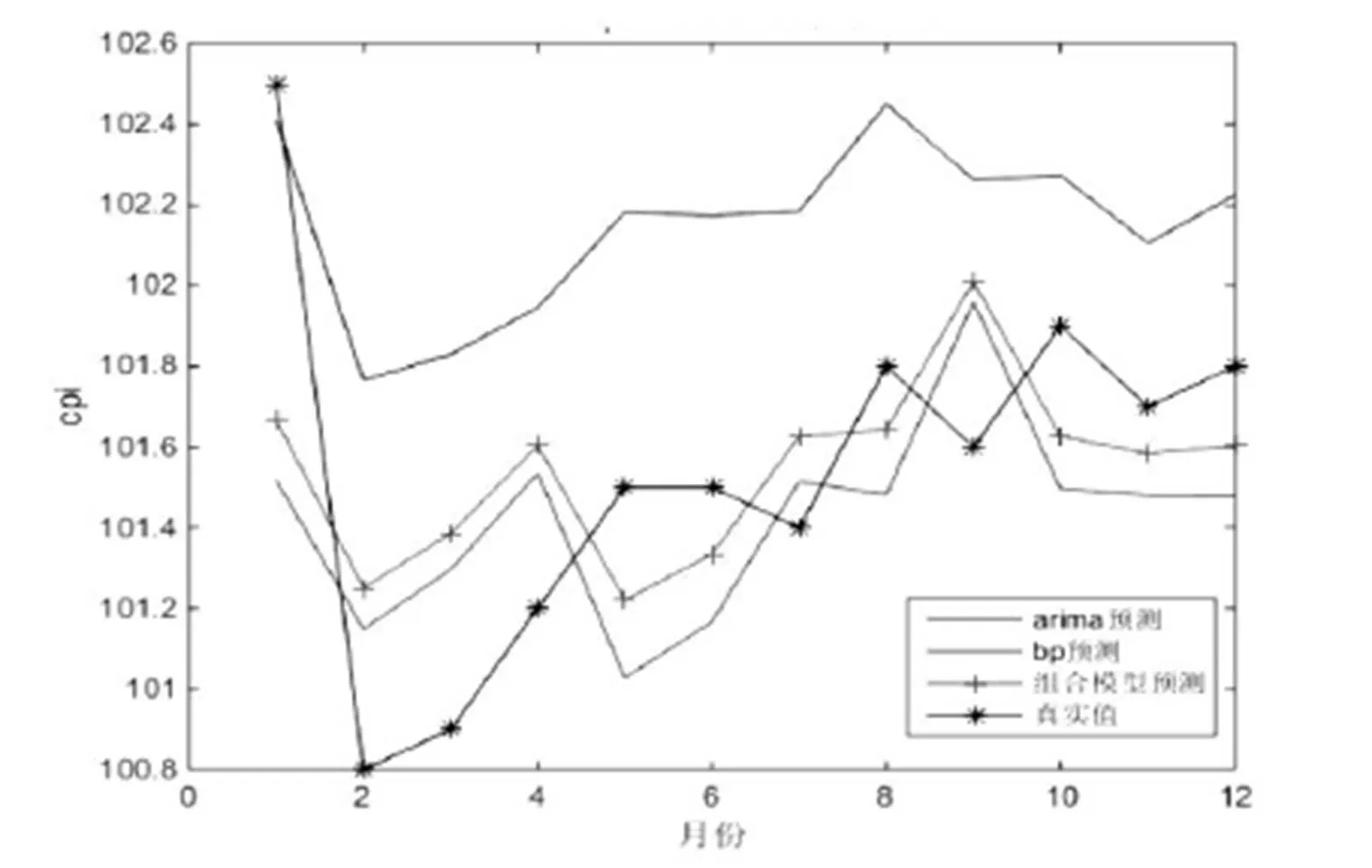
图 3 2017年三种模型CPI预测与真实值比较

表 5 三种模型相对误差

Table 5 Relative errors of three models

3 讨论

当采用动态预测时，除了第一个值是用实际值来进行预测，其他的值都是要用到前一期的预测值，所以会存在一定的不准确性。往往，动态预测只可以更好的体现出未来的趋势，而不能准确的预测。为了更好地预测居民物价消费指数，本文又建立了BP神经网络模型，然后将两者的结果组合建立模型，以消除此处ARIMA（1，1，12）预测的误差。

尽管ARIMA模型的整体趋势是与实际值最为接近，但是也是偏离程度最大的，相比较下，组合模型可以更好的预测；而与BP神经网络相比，组合模型的预测很明显更接近于真实值。与单个的ARIMA和BP神经网络预测方法比较，组合模型使用时的限定条件最少，使用范围更广泛。前两种方法都有一定的局限性，比如第二种方法在确定权重时使用了每个方法预测结果的协方差来计算，那么假设几种方法之间高度正相关，则其中一种将被给予负权重，便会导致组合预测结果大于本应有的取值范围。综上所述，ARIMA-BP组合模型比单独的模型预测效果更好。

4 结论

尽管ARIMA模型和BP神经网络模型都可以用来预测CPI，并且被广泛使用，这两种做法都有自己的不足之处。由于ARIMA序列的动态预测除了第一个值是根据真实值来预测，其余都是根据得到的预测值进一步预测，它对长时间段的预测并不精准。而BP神经网络模型整体趋势贴近真实值，但个别值不准确，变化趋势也没有ARIMA模型相像。因此本文选择把BP神经网络模型和ARIMA模型组合建立一个组合模型，目的是结合两个模型优点。经过证明我们得出了这个组合模型比其他两种模型更优的结论。

[1] 郭晓峰.基于ARIMA模型的中国CPI走势预测分析[J].统计与决策,2012(11):29-32

[2] 郑艳伟,钱乐祥,张红光,等.利用神经网络对居民消费价格指数预测的研究[J].云南地理环境研究,2006,18(6):66-70

[3] 刘海萍,王海涛,王洪利,等.基于BP神经网络的CPI预测模型[J].山东交通学院学报,2009,17(3):83-86

[4] 翟静,曹俊.基于时间序列ARIMA与BP神经网络的组合预测模型[J].统计与决策,2016(4):29-32

[5] 易丹辉.数据分析与EVIEWS应用[M].北京:中国统计出版社,2002:23

[6] 张树京.齐立心.时间序列分析简明教程[M].北京:清华大学出版社,2003:78

[7] 王燕.应用时间序列分析[M].北京:中国人民大学出版社,2005:54

[8] 汪昌云.戴稳胜.张成思.基于EVIEWS的金融计量学[M].北京:中国人民大学出版社,2010:37

[9] Box GEP, Jenkins GM, Reinsel GC,. Time Series Analysis: Forecasting and Control[M]. 5th edition. USA:Wiley,2005

[10] Andrawis RR, Atiya AF, Shishiny HE. Forecast Combinations of Computational Intelligence and Linear Models for The NN5 Time Series Forecasting Competition[J]. International Journal of Forecasting, 2011,27(3):672-688

Application of ARIMA Time Series and BP NN Combined Model in Forecast for CPI

MENG Yi

524048

The Consumer Price Index is an average that prices change with time during consumption and service in a market. Because of its influence on many economic indexes, people pay attention on it. In this paper, ARIMA time series model, BP neural network model and BP-ARIMA combined model were taken from CPI monthly data 2009-2017 in our country to forecast the monthly CPI in 2017. The result showed that forecast effect of BP-ARIMA combined model is the best in three models.

CPI; ARIMA time series; BP NN; BP-ARIMA combined model

F224.0

A

1000-2324(2018)06-1079-05

10.3969/j.issn.1000-2324.2018.06.035

2018-02-05

2018-04-06

孟毅(1982-),女,硕士研究生,主要研究方向为决策理论与应用. E-mail:26820443@qq.com