共享模式下物流联运的优化算法

王利改



共享模式下物流联运的优化算法

王利改

常州轻工职业技术学院 经贸管理学院, 江苏省 常州市 213164

在物流资源共享的背景下，物流联运优化是一个现代物流业急需解决的一个问题，本文基于图论提出一种优化算法，将物流联运网络定义成一种得到加权的网络。通过江苏省物流联运的实证分析，对本文算法与ABC算法、GA算法、BBO算法等同类型算法进行对比，在物流联运总运输量为10万t时，得到以下结果：本文算法优化后的物流联运平均成本最低，平均成本优化有较好的收敛特征。实验结果验证了本文算法的有效性。

物流联运; 资源共享; 优化算法

在现代物流中，资源共享是一项核心理念，包括货物资源的共享、运输路径的共享、运输方式的共享等。一般来说，为了提高效率和降低成本，物流企业在货物运输过程中通常会采用两种及以上的方式，使资源得到最大化的利用。如今，我国的物流行业正在朝着集约化、联盟化发展，运输方式也越来越多样化，形成陆运、水运、空运的多方联运模式，资源共享理念日益突出。物流资源共享除了要选择合适的运输方式之外，还牵涉到运输成本，这就需要对物流联运进行优化。关于这方面的优化算法及模型，相关学者进行了诸多的研究。Stank等针对物流运输的资源共享特征，对运输时间限制及路径改变等影响因素作出了分析，构建起最短运输路径的计算模型，并通过标号法求解该模型[1]。Grazia将物流服务商选择作为一个重要的因素，对多方联运的优化模型进行了构建，参与运输方式共享的各物流服务商，承载能力及收取的费用有所不同，由此设计出多层面的优化模型[2]。Chemical等提出了一种基于邻域搜索的算法，对物流联运进行测试，取得了较好的测试成果[3]。在诸多的算法中，GA算法（遗传算法）的应用比较广泛，此外还有BBO算法（生物地理学算法）、ABC算法（人工蜂群算法）等也使用得比较多。为了在前人研究的基础上有所创新，本文以图论为基础提出一种优化算法，通过物流联运网络图的构建，以本文算法与相关流行算法作对比，验证本文算法的有效性。

1 共享模式下物流联运的优化过程

1.1 共享模式下物流联运优化算法

在物流联运的网络中，有着诸多的节点，还有联运方式所构成的边。共享模式下的物流联运优化算法模型，可以通过图的方式实现定义。根据图论把物流联运网络定义成一种得到加权的网络，用(,,,)表示。是物流联运的节点集合，是联运路径的集合，是路径成本的权重集合，是路径容量的约束集合。关于物流联运的优化目的，就是需要在得到加权的网络里选择包含运输方式在内的多种路径，然后在路径上分配物流资源，最终使资源得到充分的共享。在这种情况下，能够达到最少的运输成本。本文提出的共享模式下物流联运优化算法如下：

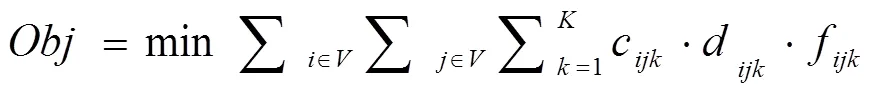
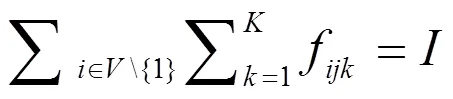
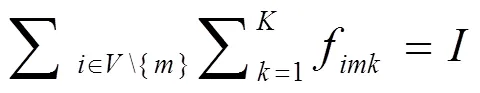
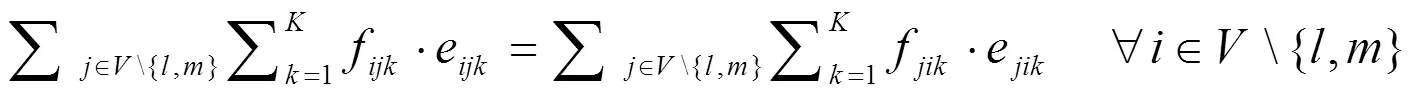
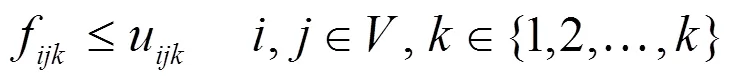
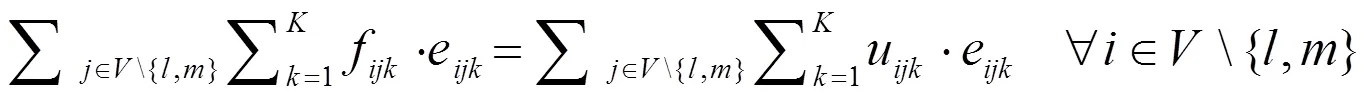
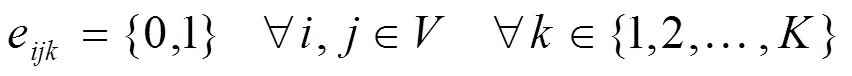
在以上模型函数中，是物流联运的输入运量；是节点的数量；是运输方式，Î{1,2,…,}，此次实验用=3代表公路、铁路、水路联运方式；c是联运网络中节点与节点之间通过运输方式所产生的运输成本；u是联运网络中节点与节点之间通过运输方式所形成的容量上限；f是联运网络中节点与节点之间通过运输方式所形成的流量；d是联运网络中节点与节点之间通过运输方式所形成的运输距离；e为变量，取值0~1，当值为1，代表联运网络中节点与节点之间通过方式进行运输，值为0时则不是。

公式（1）用于计算最小化模式下联运的总成本；公式（2）用于计算输入运量的约束值；公式（3）用于计算目标节点的总运输量；公式（4）用于计算各节点流量的平衡值；公式（5）用于计算节点与之间最大运量的约束值；公式（6）用于计算最大运量对节点运量的约束值；公式（7）用于计算节点与之间联运方式的约束值；公式（8）用于计算变量的定义值。

1.2 共享模式下物流联运整体流量的比例分配

物流联运受到流量平衡与路径约束等一些条件的限制，这在一定程度上会导致方案的不可行，降低算法搜索能力。所以在共享模式下构建物流联运优化流程，需要对整体流量的比例进行分配。设联运网络中任意一个节点一维数=(1,2,…,x)，xÎ。整体流量比例分配就是要解码，以提高联运方案的可行性与有效性。对于整体流量的比例分配来说，需要将每个节点流量的分配看作优化对象。第一步是分配排序联运网络中的边，用方程=(1,2,…,f)进行计算，使方程（1）里面的f按照实际的运输路径进行转化，形成相对应的。整体流量比例分配如图1所示。

图 1 物流联运整体流量比例分配图

假设从节点1输出的流量是1，其它4个节点为下级节点，流量分配的比例为r=(Î{1,3,4,5,6})，节点1向各个下级节点所输出的流量用1·计算，其中=(1,3,4,5,6)。据此，对每一种运输方式与的关系进行构建，形成一定的映射关系。的计算公式如下：

在上式中，Class代表输出节点是的时候，同一个层次所有运输路径的集合。以各路径流量分配的比例为基础，计算任意一条路径的流量：f=Outflow·r(10)

在上式中，s代表节点在路径上总的输出流量。如在图1中，节点1与下级节点4的路径是4，同一层次的路径1={1,3,5,6}，按照公式（9），4=4/åx，Î1。然后按照公式（10）计算出4分配到的流量4=1·4。这样就成功实现了流量分配。

2 实验分析

2.1 实验案例的选取

实验以江苏省物流联运为例，对本文提出的优化算法进行验证。江苏省作为我国沿海对外开放省区，经济发展快速，交通运输业也极为发达，形成了陆运、空运、水运一体化的发展态势，为物流联运创造了良好的条件。江苏省物流联运网络如图2所示。

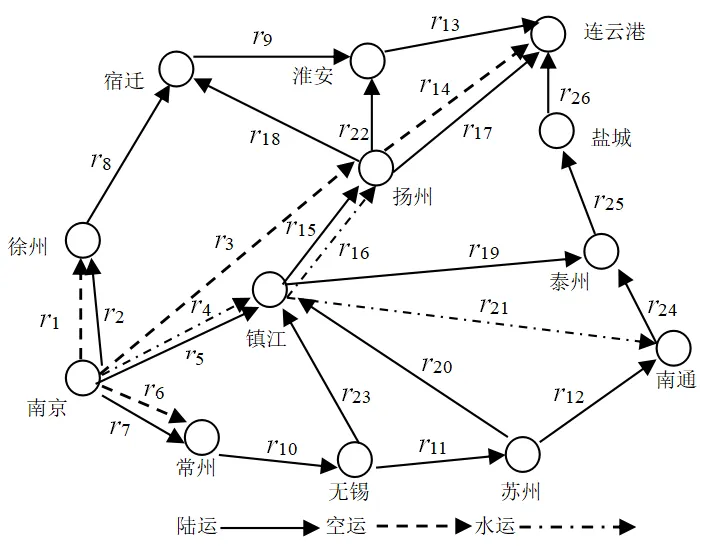
图 2 江苏省物流联运网络图

从图2可以看出，物流联运节点共有13个，涵盖了江苏省13个地级市。南京是物流联运的起点，连云港是物流联运的终点，其它则为中间节点。由于江苏省所有地级市都已通铁路和高速公路，从南京出发，陆运可以抵达每一个节点城市。在空运方面，从南京可以抵达常州、徐州、扬州、连云港。在水运方面，从南京沿着长江航道，可以抵达镇江、扬州和南通。镇江是陆运和水运的一个集散点，而扬州则是陆运、空运、水运的一个集散点。

2.2 设置算法对比参数

为了验证本文提出的物流联运优化算法有效性，选择了ABC算法（人工蜂群）、GA算法（遗传）、BBO算法（生物地理学）等同类型算法进行对比。表1设置了各算法的参数，节点数=13，迭代的最大次数=1000。所有算法都以Matlab R2017B商业数学软件进行统一的测试，独立运行每个算法15次，最后进行数据统计。

表 1 各类算法的参数设置

注：ABC算法、GA算法、BBO算法参数设置分别来自文献[4]、文献[5]、文献[6]。

Note: The parameters of ABC, GA, BBO algorithm came from references [4], [5],and [6], respectively.

2.3 实验结果

设物流联运的总运输量为10万t，本实验的算法对比结果如表2所示，平均成本优化的收敛曲线图如图3所示。用本文算法进行优化的结果，物流联运平均成本最低，明显优于其它算法。从平均成本优化的收敛曲线图看，本文的算法具备较好的收敛特征。在算法的搜索初期，尽管以上算法的搜索速度都比较快，但本文算法的收敛速度更快，无限接近于最优。在算法的搜索后期，本文算法可以继续进行快速的搜索，而其它算法的搜索速度明显放缓，说明本文算法得出的优化结果有着更高的收敛精度，能够对更多的区域进行搜索，从而提升了优化的能力，形成良好的适应性。

表 2 本实验的算法对比结果（运量：吨；成本：元/吨每公里）

图 3 平均成本优化的收敛曲线图

3 讨论

关于资源共享模式下物流联运优化算法的研究，比较流行的算法有ABC算法、GA算法、BBO算法等。ABC算法模拟的是蜂群采食的交流行为，该算法的最主要特征是无需了解计算对象的一些特殊信息，只需比较问题的优劣性，由此得出局部的寻优行为，最终突出全局的寻优值[4]。GA算法是对自然选择与生物进化进行的模拟，遵循遗传学机理，以达到过程搜索的最优解[5]。BBO是一种基于生物地理学的算法，这种优化算法对自然界生物分群及迁移的特征进行模拟，对于空间搜索比较有效[6]。从本次实验结果看，GA算法最接近本文算法，而ABC算法则相差较远。鉴于GA算法的随机化搜索特性以及在智能计算中的关键地位，在今后的创新改进中，可以多借鉴GA算法的相关理论。

4 结论

针对资源共享模式下物流联运的优化问题，本文基于图论提出一种优化算法，将物流联运网络定义成一种得到加权的网络，由节点集合、路径集合、路径成本集合、路径容量约束集合组成。算法要素包括输入运量、节点数量、联运方式、运输成本等。实验以江苏省物流联运为例，对本文提出的优化算法进行验证。通过本文算法与ABC算法、GA算法、BBO算法等同类型算法的对比，在物流联运的总运输量为10万t时，实验结果如下：本文算法优化后的物流联运平均成本最低，明显优于其它算法；本文算法的平均成本优化有较好的收敛特征，在算法搜索初期，收敛速度无限接近于最优，在算法搜索后期，可以继续进行快速的搜索。

[1] Stank TP, Pellathy DA. In J,. New Frontiers in Logistics Research: Theorizing at the Middle Range[J]. Journal of business logistics, 2017,38(1):6-17

[2] Speranza MG. Trends in transportation and logistics[J]. European Journal of Operational Research, 2018,264(3):830-836

[3] Chemical Weekly Group. Govt, working on integrated logistics portal[J]. Chemical Weekly, 2018(26):146-156

[4] Hong PN, Ahn CW. Linkage artificial bee colony for solving linkage problems[J]. Expert Systems with Application, 2018,61(4):378-385

[5] Ahmadi MR, Shahabi RS. Cutoff grade optimization in open pit mines using genetic algorithm[J]. Resources policy, 2018,55(6):184-191

[6] Aljarah I, Faris H, Mirjalili S,Training radial basis function networks using biogeography-based optimizer[J]. Neural computing & applications, 2016,27(7):529-553

Optimal Algorithms of Intermodal Logistics under a Shared Mode

WANG Li-gai

213164,

Under the background of logistics resource sharing, intermodal logistics optimization is an urgent problem to be solved in modern logistics industry. This paper proposes an optimization algorithm based on graph theory, which defines intermodal logistics network as a weighted network. Through the empirical analysis of intermodal logistics in Jiangsu Province, this paper compares the algorithm with ABC algorithm, GA algorithm, BBO algorithm and other similar algorithms. When the total volume of intermodal logistics is 100,000 tons, the following results are obtained: the average cost of intermodal logistics optimized by this algorithm is the lowest, and the average cost optimization has better convergence characteristics. The experimental results verify the effectiveness of the proposed algorithm.

Intermodal Logistics; resource sharing; optimal algorithms

U15

A

1000-2324(2018)06-0991-04

10.3969/j.issn.1000-2324.2018.06.017

2018-01-12

2018-03-04

王利改(1981-),女,硕士,讲师,主要研究方向为物流管理. E-mail:wlg013013@163.com