基于VA One船舶舱室动力设备空气噪声控制分析
胡凡,车驰东,李正阳
(上海交通大学 动力装置及自动化研究所,上海 200240)
随着现代化船舶对安全性及舒适性要求的不断提高,船舶舱室噪声的预报及控制在船舶设计阶段受到越来越多的关注。根据国际海事组织(IMO)最新的《船上噪声等级规则》,对于10 000总吨级以上的船舶,其噪声上限值均在原来的基础上降低了5 dB,增加了噪声控制的难度[1]。因此,船舶早期声学设计的重要性日益突出,若能在船舶总体设计阶段及早发现噪声超标隐患,则可极大降低后续设计阶段的噪声控制成本。
船舶噪声的传播主要有两种途径:1)结构声传播,即动力设备工作时产生的结构噪声,然后通过刚性连接由船舶结构向其他舱室传播;2)空气声传播,即动力设备工作时产生空气噪声,然后通过空气或者其他介质透过舱壁传播至其他舱室[2-3]。由于声音也是机械振动能量的一种形式,当能量从声源产生,进而经过若干条传播途径到达接收者,此过程也是噪声源能量从产生到耗散的一个过程[4]。按照声源-路径-接受者这个过程分析,控制噪声也就有三种途径:声源噪声的控制、传播途径的控制、接受者噪声防护设备的使用。
目前在船舶舱室噪声控制方面,对于阻尼与吸声材料在复合结构板中对隔声性能的影响研究较少,因此文中研究的重点在于阻尼复合板的隔声性能[5]。主要从噪声传播途径的控制展开,利用VA One软件建立舱室统计能量分析(SEA)模型,对舱室壁板隔声性能进行研究,分析不同约束条件及敷设方式对于舱壁隔声量的影响,为舱室动力设备空气噪声控制措施提供参考。
1 两个子系统SEA模型
统计能量分析中的子系统必须是可贮存振动能量的子系统,由这些子系统组成的统计能量分析模型可以表示出该模型能量的输入、储存、耗损和传输的特征[6]。
1)单个子系统。对单个子系统的损耗功率Pd有如下基本关系:
式中:ωn为振子固有频率;E为能量;η为内损耗因子。
2)两个子系统。图 1为由两个子系统耦合而成的系统,其中一个子系统由外载荷直接激励,另一个子系统则仅是通过耦合来驱动的。
两个子系统间能量平衡方程为:
式中:P为系统输入能量;ηij为耦合损耗因子;n为模态密度;E为能量;ω为分析频段的中心频率;ηi为阻尼损耗因子。
通过计算将阻尼损耗因子代入统计能量分析平衡方程,求解方程得到各子系统的能量,再利用声腔子系统质点振动速度、声压和能量之间的关系式(3)求出某声腔子系统的声压[7-9]。
式中:m为板质量;V为声腔体积;ρ为空气密度;c为声速。
2 舱室间空气声传递损失计算
空气声隔声是噪声控制中最常用的技术之一,包围船舶舱室间的舱壁结构,本身就具有一定的隔声性能。其隔声效果在一定程度上决定了舱室内的噪声等级,是计算舱室噪声水平的重要参数。
图2为两相邻舱室间空气声传递示意图。在计算与声源相邻舱室的空气噪声时,受声室的声压级可表示为:
式中:Lp,S为声源室声压级,dB;δTL为舱室间的传递损失,dB;S为声源室与接受室之间的隔板面积,m2;AE为受声室的总吸声面积,m2。
船舶舱室中空气声的传播受到舱室边界和其他物体的反射,同时还受到其他声波的干扰,室内声波不再遵循自由声场中的传播规律。为了便于计算,通常假设船舶舱室噪声声源为平均声能处相等的扩散声场,则式(4)中 δTL为隔板隔声量,它是入射到隔声结构与投射过隔声结构的声功率差,是工程中最常使用的评价结构隔声性能的指标[10],其计算公式为:
式中:Wi为声源室入射声功率,W;Wt为透射声功率,W;τ为透射系数。
3 典型舱室隔声性能分析
3.1 数值分析模型
在船舶进行减振降噪处理时,大量使用粘弹性阻尼材料,根据其阻尼结构形式的不同可以分为两种基本形式:一种是阻尼材料或者阻尼层直接添加在基材的表面,称为自由阻尼;另一种是在自由阻尼层的基础上又添加一层弹性模量远远大于阻尼层的约束层,称为约束阻尼。自由阻尼结构其原理主要是阻尼材料随着基材振动而发生拉伸变形,从而起到减振的作用;约束阻尼结构其原理是随着自由阻尼的拉伸变形,依靠约束层和自由阻尼的相对位置使阻尼层产生剪切变形,从而起到减振的作用[11-12]。两种结构如图3所示。
针对自由阻尼和约束阻尼结构的隔声效果,在舱壁厚度一定的条件下,建立两个舱室的 SEA模型。定义板结构的尺寸为3 m×3 m,两侧声空间尺寸均为5 m×5 m×4 m,如图4所示。其中左边是声源室,右边是受声室,中间为一块使用粘弹性阻尼材料的粘接复合板。复合板金属层材料选用的是钢板,阻尼层选用的材料为橡胶板,两种材料的属性见表1。

表1 复合板材料属性
3.2 隔声量分析
在不考虑温度和频率等对阻尼性能的影响下,选取31.5~8000 Hz之间的9个倍频程作为主要的分析频带。设定自由阻尼结构参数为:100 mm钢板+50 mm阻尼层;约束阻尼结构参数为:50 mm钢板+50 mm阻尼层+50 mm钢板。图5和表2为两种不同阻尼结构对应的隔声量。

表2 两种结构隔声量
分析结果显示,约束阻尼结构隔声量A计权声压级比自由阻尼结构高出约 1.1 dB,说明对于 0.15 m厚壁板而言,约束阻尼结构其隔声性能要好于自由阻尼结构。为了探究此结果对于不同厚度壁板的适用性,选择不同厚度壁板作进一步分析。图6和表3、表4分别为0.09 m厚与0.25 m厚壁板两种结构的隔声量数据,对应的结构参数为:40 mm钢板+50 mm阻尼层,20 mm钢板+50 mm阻尼层+20 mm钢板;200 mm钢板+50 mm阻尼层,100 mm钢板+50 mm阻尼层+100 mm钢板。

表3 0.09 m壁板两种结构隔声量

表4 0.25 m壁板两种结构隔声量
从上述结果可知,两种结构的隔声性能是随着壁板厚度的变化而变化。对于0.09 m壁板,自由阻尼结构隔声量A计权声压级比约束阻尼高出约1.6 dB;对于0.25 m壁板,约束阻尼结构隔声效果则更好。根据以上分析,对于高频噪声,约束阻尼结构隔声效果总是优于自由阻尼结构。当壁板厚度较低时,自由阻尼结构 A计权隔声效果更好。随着厚度的增加,约束阻尼结构优势更加明显。
如图7所示,将自由阻尼结构金属层和阻尼层之间的相对位置进行调整,分析其隔声性能的变化,图8为分析结果。根据图7显示,自由阻尼结构改变金属层和阻尼层的相对位置,对其隔声性能没有任何影响。
在保证阻尼层厚度和壁板总厚度不变的条件下,对约束阻尼结构两侧金属层厚度作进一步分析,厚度差对隔声量的影响见表5。从表5可以看出,采用两侧金属层厚度方式敷设时,约束阻尼结构的隔声性能是最好的。随着厚度差的增大,其隔声效果也逐渐降低。
4 结论
文中建立了两相邻舱室的 SEA模型,讨论了约束阻尼结构和自由阻尼结构对壁板隔声性能的影响。通过VA One软件计算结果比较可见,在阻尼层厚度和壁板总厚度一定时:1)对于高频噪声,约束阻尼结构隔声效果总是优于自由阻尼结构;2)对自由阻尼结构,金属层与阻尼层之间的相对位置对实际的隔声性能并没有影响;3)对于约束阻尼结构,两侧金属层等厚敷设时,其隔声效果最优,且两侧厚度差越大隔声量越小。
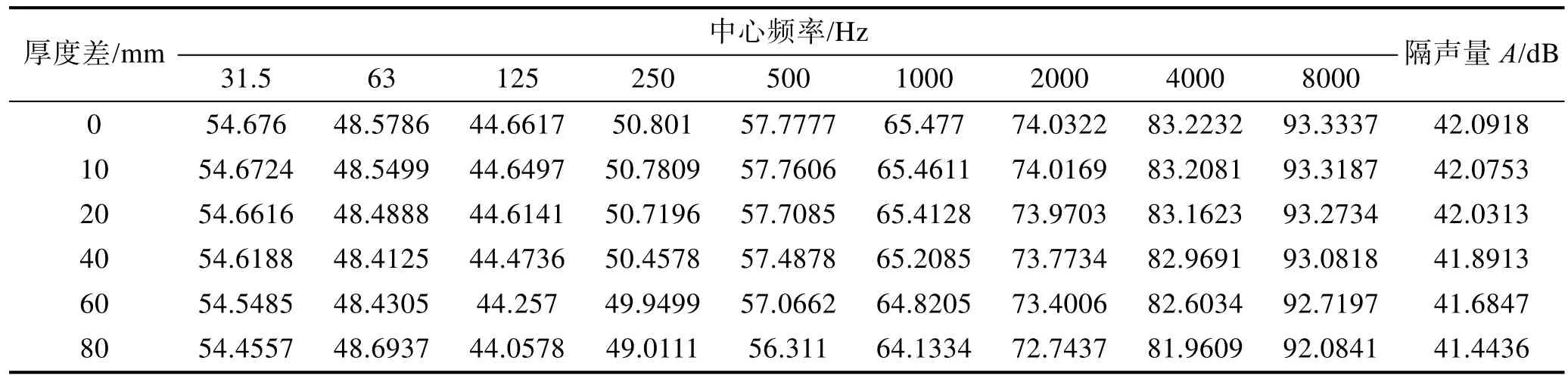
表5 厚度差对隔声量的影响

