水溶液中超高速纳米齿轮的分子动力学模拟

梁栋，付中玉，孙康，徐震

摘  要： 本文根据在旋转电场的诱导下，悬浮于水溶液中的碳纳米管可以借助于水偶极子方向能够发生旋转这一原理提出一种超高速、易组装、摩擦力小的T型纳米马达转子，并在纳米马达转子的基础上设计出新型纳米齿轮传动系统。该纳米齿轮传动系统可应用于全部为水溶液或者部分为水溶液的工作环境。通过Gromacs软件仿真结果发现，调整旋转电场转速或者改变旋转电场场强可以减小纳米马达转子与水分子偶极之间的滞后角，使得纳米马达转子在最短时间内与旋转电场步调保持一致。该模拟仿真结果对于纳米齿轮的应用以及复杂机构纳米旋转设备的设计有着重要参考价值。

关键词： T-型马达;分子动力学;纳米齿轮;旋转电场;超高速设备

中图分类号： TP271+.3    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.12.014

本文著录格式：梁栋，付中玉，孙康，等. 水溶液中超高速纳米齿轮的分子动力学模拟[J]. 软件，2019，40（12）：6165

Molecular Dynamics Simulation of Ultra-high Speed Nanogear in Aqueous Solution

LIANG Dong， FU Zhong-yu， SUN Kang， XU Zhen*

（Shanghai University of Engineering Science， Shanghai 201620）

【Abstract】： Based on the principle that carbon nanotubes suspended in aqueous solution can be rotated by the principle of water dipole， a T-type nanomotor with ultra-high speed， easy assembly and low friction is proposed. The new nanogear transmission system is designed on the basis of the nanomotor rotor. The nanogear transmission system can be applied to a working environment in which all are aqueous solutions or partially aqueous solutions. Through the simulation results of Gromacs software， it is found that adjusting the rotating electric field speed or changing the rotating electric field strength can reduce the lag angle between the nanomotor rotor and the water molecule dipole， so that the nanomotor rotor is consistent with the rotating electric field in the shortest time. The simulation results have important reference value for the application of nanogears and the design of nano-rotating equipment in complex mechanisms.

【Key words】： T-type motor; Molecular dynamics; Nanogear; Rotating electric field; Ultra-high speed devices

0  引言

由于納米尺度下的物质表现出很多新颖甚至奇异的特性[1]，使得纳米器件的性能有别于宏观器件。另外，纳米齿轮[2-8]是纳机电系统不可缺少的一部分，如纳米机器人、分子汽车、纳米水泵等[9-12]。因此，近些年来，纳米齿轮已引起了许多领域学者的广泛关注，成为热门的研究课题。

宏观机械齿轮在许多机械设备中主要用来产生和控制旋转运动，例如钟表、手表、变速箱、汽车、机器人等等。在微观层面上，有两种齿轮，分子齿轮和纳米齿轮。分子齿轮是以分子中的单键作为旋转轴，这样的分子单键为分子齿轮的合成提供了设计经验，同时也为纳米齿轮的研究提供了理论基础。苯与C60的发现刺激人们产生纳米齿轮的想法。碳纳米管的高稳定性以及丰富多样的苯的衍生物使得人们有着非常浓厚的兴趣研究纳米齿轮。Md.Hasan等人[13]一种樱花状的纳米齿轮。该设计是通过水热反应合成与/或型碳纳米管，结合含有Ca2+离子的硝酸盐溶液形成具有立方体或六边形相位LaCo3OH晶体的纳米齿轮结构。Weng等人[14]发现乙醇和醋酸镍形成的自组织微/纳米结构含有四边形、六边形、纳米齿轮、纳米颗粒、球体和异常结构，并根据定向的自我组织性质首次提出使用火焰燃烧技术制作纳米齿轮和轮胎。虽然在溶液中的纳米齿轮已有一些成果，但是对于如何精准驱动控制纳米齿轮却还没有进行详细的描述。

近些年来，由于碳纳米管的独特特性[15-21]，以碳纳米管为基础的纳米齿轮传动系统受到了人们的广泛关注。Han等人[4]用碳纳米管和苯环相结合设计出纳米齿轮轴。该设计利用温度驱动齿轮和齿轮轴，并发现降低温度或转速可使失效齿轮恢复运行，此设计对于纳米齿轮系统的进一步研究有着重要作用。根据Guo等人[22]研究的CNT定向机制，当含有CNT的水溶液体系施加电场时，CNT在水分子偶极的驱动下迫使它的表面朝向电场，此成果为利用电场驱动水中CNT马达转子的实现铺平了道路。Rahman等人[6]根据在旋转电场的诱导下，浸没于水溶液中的碳纳米管可以借助于水偶极子方向能够发生旋转这一原理设计出一种分子叶片螺旋桨以及用于驱动外载荷的纳米齿轮系统，然而对于其他形状的纳米马达齿轮的结构设计却没有进行介绍。

本文将（10， 10）扶手型碳纳米管组合成T型纳米马达转子[23]，并在T型马达转子的基础上，将6个苯分子连接到翼CNT上作为纳米齿轮的齿，两个纳米齿轮通过苯齿进行机械耦合。该研究用分子动力学的方法对水溶液中的纳米齿轮体系进行分子动力学模拟，探究纳米齿轮的转速、转角、周期的影响。本文的模拟结果对溶液中纳米旋转设备的设计有着重要的参考作用。

1  模型及数值方法

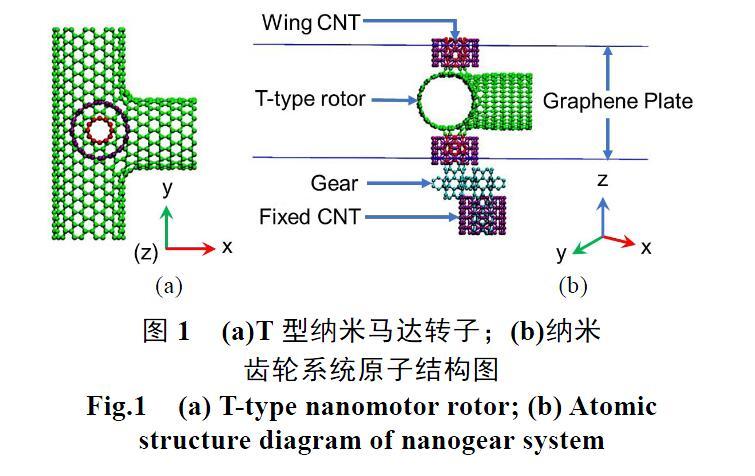
本文使用的物理模型如图1所示，红色部分表示纳米马达翼CNT;紫色部分表示固定CNT用于对纳米马达转子的固定;蓝色部分表示石墨烯板，主要用于将放置于水溶液中的纳米马达转子与外部空间进行隔开;青色部分表示苯环与碳纳米管组合成的纳米齿轮。本研究中我们选用7 nm×7 nm的石墨烯板作为纳米马达转子的隔板，选择长7 nm（10， 10）型的碳纳米管作为中央CNT，并选用长度为0.71 nm手性为（6， 0）的碳纳米管作为纳米马达旋转轴的两个“CNT翼”，我们在一些翼CNT上“安装”苯环作为纳米齿轮的齿，纳米马达的两翼CNT保持在两个长度为0.37 nm手性为（8， 8）的“固定碳纳米管”内，这些固定的碳纳米管可以对两翼CNT旋转起到支撑作用。在实际的环境中，固定CNT会连接到一些刚性支撑。

（a）                            （b）

圖1  （a）T型纳米马达转子;（b）纳米

齿轮系统原子结构图

Fig.1  （a） T-type nanomotor rotor; （b） Atomic

structure diagram of nanogear system

我们选定XY平面作为纳米马达的旋转平面，并且在X轴和Y轴分别构建了一个正交变换的电场（当两个变换电场复合后可以实现旋转效果）。正交电场的函数表达式为：Ex=Et cos（ωt），Ey=Et sin（ωt）式中Ex，Ey表示复合计算后的场强，Et表示初始设定的电场强度，ω表示正交电场变化的角速度，t表示正交电场变化的时间。实际中我们可以通过调整交流电的相位角，实现正交电场的构建，此方法Fan等人[24，25]已经使用。

此次模拟我们借助于Gromacs5.1.4软件完成分子动力学模拟[26-30]，模拟所用的系综是NVT，即保持原子数、体积和温度不变，其中温度由速度标定法（V-rescale）控制在300 K左右。另外，模拟过程中使用Amber99sb-ildn力场和被认为是不带电的Lennard-Jones（LJ）碳原子颗粒相结合描述非键合相互作用势，碳-碳之间使用的LJ参数为：σCC=0.34 nm，εCC=0.3664 kJ·mol–1。碳纳米管和水分子之间的相互作用采用碳原子和氧原子之间的LJ势能来进行描述。碳-氧原子之间LJ参数为：σCO=0.3275 nm，εCO=0.4772 kJ·mol–1。在模拟计算中，LJ势能采用截断算法，其截断半径为1 nm。与其他算法性比[29，31-38]，原子之间采用静电相互作用采用Particle-Mesh- Ewald（PME）算法得出结果的性能较好[39]，其中短程作用的截断半径为1 nm，并将时间步长为2 fs，数据采集频率为每隔0.5 ps记录一帧。

2  分析与讨论

根据纳米马达在水溶液中的旋转机理（在电场作用下，水分子的偶极子为使自身氢键最大化迫使CNT的表面朝着电场方向一致，从而使中央CNT转子在水分子偶极驱动下产生旋转），因此我们绘制了当旋转电场强度为1 v/nm，速度为1.75×1011 rpm时，T型纳米马达转子周围水分子在X、Y、Z方向上的平均偶极矩曲线（如图2（a）所示）。在图2（a）中可以看到，px与py相位差为90°，两者随时间变化的曲线满足正余弦曲线变化规律，这与构造的正交电场函数变化相一致。由于XY平面为旋转平面，Z轴方向没有旋转电场作用，因此pz基本位于零值。在图2（b）中可以看到，在0～2.5 ns的时间段内，纳米电机转子的转角随时间增大呈直线式上升，而在2.5～5 ns时间段内，当不施加电场后，纳米马达转子的转子转角也不再增大。此结果表明，所构建的旋转电场可以对水溶液中纳米马达转子起到导向作用。

（a）                           （b）                          （c）

图2  （a）平均偶极强度随时间的变化曲线;（b）T型纳米马达转子转角随时间的变化曲线;

（c）T型纳米马达转子周围净水偶极子转角以及马达转子转角随时间的变化曲线

Fig.2  （a） Average dipole intensity versus time curve; （b） T-type nanomotor rotor angle versus time curve;

（c） T-type nanomotor rotor around the water dipole corner and motor rotor angle Curve of change over time

在图2（c）中可以看到，当旋转电场强度为1 v/nm，速度为1.75×1011 rpm时，T型纳米马达转子转角相对于马达转子周围水分子偶极转角滞后130°，该滞后角是由于施加电场后，水分子的偶极子为使自身氢键最大化，需要调整自身导向迫使CNT的表面朝着电场方向一致所形成。相关研究表明，对于足够低的旋转速度，CNT旋转可能几乎是同步的，而当施加更高的速度（直到最大速度）时，在水偶极子取向和CNT之间存在一定的滞后角度，二者是不同步的。因此我们可以通过改变旋转电场的速度调整滞后角，实现二者转速同步，提高纳米电机效率。

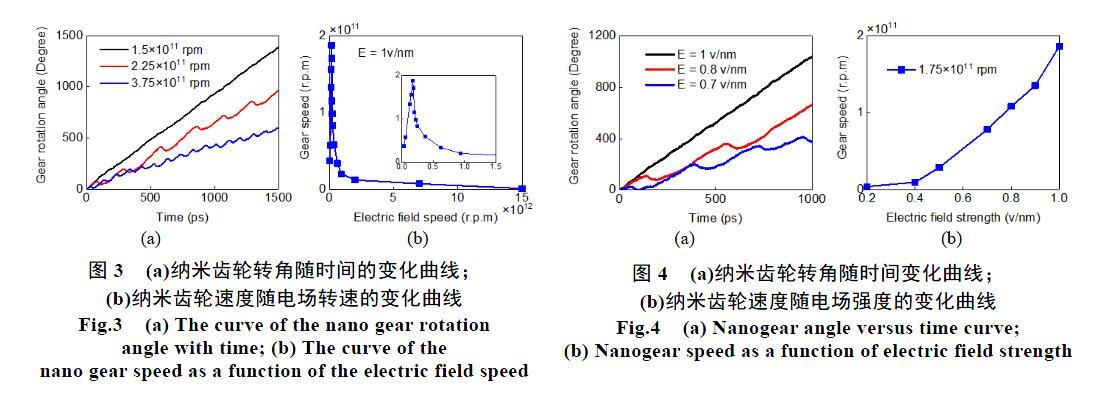
通过图3（a）可以发现，当施加不同转速的旋转电场时，随着旋转电场的转速增大，齿轮转角曲线的波动性更加明显。这是因为当旋转电场速度足够低时，CNT转子旋转可以跟旋转电场步调保持一致，因为纳米齿轮与CNT转子同轴相连，所以纳米齿轮与旋转电场的转角也可以保持同步，纳米齿轮的转角曲线不会产生太明显的波动;当旋转电场速度太高，导致纳米马达转子不能“锁定”旋转电场步调，两者之间就会存在一定的角度滞后，造成纳米齿轮转角曲线出现不同程度的波动。通过当旋转电场强度为1 v/nm时，纳米齿轮速度随电场转速的变化曲线（如图3（b））可以发现，随着旋转电场转速的增大，齿轮转速先增大然后直至减小接近于零，此结果与Rahman等人[6]模拟的结果相一致。这是因为随着旋转电场速度增大，纳米马达转子出现明显的滞后效应（滞后效应表示纳米齿轮在旋转过程中出现向前向后运动），导致纳米齿轮的旋转周期变大。根据n=1/T（n为纳米齿轮的转速，T为纳米齿轮的周期）可以知道，齿轮的周期越大，速度就会越小。所以，图3（a）解释了图3（b）纳米齿轮在旋转电场的速度达到一定值之后，齿轮速度会呈现下降趋势的原因。

通过在不同电场强度下，纳米齿轮转角随时间变化曲线（如图4（a）所示），當旋转电场强度为1 v/nm时，纳米齿轮的转角曲线基本没有太大的波动，纳米齿轮可以锁定旋转电场的步调，而当电场强度为0.8 v/nm和0.7 v/nm时，纳米齿轮的旋转曲线都出现不同程度的波动，纳米齿轮出现滞后效应，不能跟上旋转电场的步调。可以看出，随着旋转电场强度增大时，纳米齿轮转角随时间的变化曲线的波动性逐渐变小。因此，对于特定转速的旋转电场，可以通过调整旋转电场的强度调整纳米齿轮的转角，实现对纳米齿轮的控制。当旋转电场转速为1.75×1011 rpm时，在不同电场强度下纳米齿轮速度随电场强度的变化曲线（如图4（b）），可以发现，当特定旋转电场转速条件下，旋转电场电场强度越小，纳米齿轮的转速越小。随着旋转电场强度的增大，纳米齿轮转速整体呈现增大趋势。因此，当旋转电场转速确定时，可以通过调整旋转电场的场强对纳米旋转齿轮进行控制。另外，该研究结果对于水溶液中复杂结构纳米齿轮传动系统的设计有着重要参考价值。

（a） （b） （a） （b）

图3  （a）纳米齿轮转角随时间的变化曲线;

（b）纳米齿轮速度随电场转速的变化曲线

Fig.3  （a） The curve of the nano gear rotation

angle with time; （b） The curve of the

nano gear speed as a function of the electric field speed

图4  （a）纳米齿轮转角随时间变化曲线;

（b）纳米齿轮速度随电场强度的变化曲线

Fig.4  （a） Nanogear angle versus time curve;

（b） Nanogear speed as a function of electric field strength

为了更好地体现纳米齿轮在一个周期内的旋转过程，我们选择当旋转电场强度为1 v/nm，速度为1.75×1011 rpm时，纳米齿轮在一个周期内不同时刻两齿轮的啮合状况进行截图（主动轮用红蓝（红色和蓝色）颜色进行标记，从动轮用黄紫（黄色和紫色）颜色进行标记）（如图5（a）所示）。当旋转电场强度为1 v/nm时，纳米齿轮体系中马达转子与水溶液相互作用能随旋转电场速度的变化曲线（如图5（b）所示），可以看出，纳米齿轮体系中马达转子与水溶液之间的相互作用能随着旋转电场转速的增大而增大。另外，当旋转电场转速介于3×1010～2.5× 1011 rpm范围内，相互作用能曲线的斜率大于在2.5×

1011～15×1012 rpm范围内相互作用能变化曲线斜率，说明在3×1010～2.5×1011 rpm范围内，旋转电场速度对纳米齿轮体系中纳米马达转子与水溶液相互作用能变化产生较大影响。图5（c）表示当旋转电场速度为1.75×1011 rpm时，纳米齿轮系统中马达转子与水溶液相互作用能随旋转电场场强的变化曲线。可以看出特定旋转电场转速条件下，纳米齿轮体系中纳米马达转子与水溶液相互作用能随着旋转电场场强的增大而增大。根据Guo等人[22]和Winarto等人[27]的研究结果可以知道，较强的旋转电场可以使得纳米马达周围的水分子出现较高程度取向。因此，当设计复杂结构的纳米齿轮旋转设备时，可以通过调整旋转电场转速使得纳米马达周围的水分子偶极矩方向在较短时间可以与旋转电场方向相一致，另外，也可以通过改变旋转电场场强的大小调整纳米马达周围的水分子偶极矩定向时间。

（a）                              （b）                            （c）

图5  （a）纳米齿轮的不同时刻位置截图;（b）相互作用能随电场速度的变化曲线;（c）相互作用能随电场场强的变化曲线

Fig.5 （a） Screenshot of the different moment positions of the nano gear; （b） The curve of the interaction energy

with the electric field velocity; （c） The curve of the interaction energy with the electric field strength

3  結论

本文所提出的超高速T型纳米马达的工作环境可全部为水溶液，也可以部分为水溶液，扩大了纳米齿轮体系使用范围，而且还具有超高速、易组装、摩擦力小等优点。根据纳米齿轮体系的分子动力学模拟结果发现，可以通过改变旋转电场场强大小以及旋转电场转速实现对纳米齿轮的转角、转速进行控制，使得纳米齿轮在旋转过程中可以与旋转电场的步调保持一致，从而提高纳米齿轮传动系统的工作效率。

通过对纳米齿轮体系的进一步研究，加深了我们对水-碳纳米管体系的进一步理解，这些发现可以帮助我们更好的实现对复杂结构纳米齿轮体系进行精准控制，同时也可以在此基础上设计出新型的纳米流体机器、纳米汽车等等。

参考文献

[1]白春礼. 纳米科技及其发展前景[J]. 世界科学， 2001， 52（4）： 37-37.

[2]孙玮， 张晋江， 赵健伟. 纳米器件的分子动力学模拟[J]. 物理化学学报， 29（9）： 1931-1936.

[3]Li Y， Liu Y， Wang Q， et al. Geometry and energetics of nano gears[J]. Journal of Computational and Theoretical Nanoscience， 2010， 7（8）： 1457-1461.

[4]Han J， Globus A， Jaffe R， et al. Molecular dynamics simulations of carbon nanotube-based gears[J]. Nanotechnology， 1997， 8（3）： 95-102.

[5]Tas?c? E， Bar?s O， Malc?og?lu， et al. Structural properties of carbon nanogears[J]. Fullerenes， Nanotubes and Carbon Nanostructures， 2008， 16（1）： 30-39.

[6]Rahman M M， Chowdhury M M， Alam M K. Rotating-  electric-field-induced carbon-nanotube-based nanomotor in water： a molecular dynamics study[J]. Small， 2017， 13（19）： 1603978.

[7]Robertson D H， Dunlap B I， Brenner D W， et al. Fullerene/ Tubule based hollow carbon nano-gears[J]. MRS Online Proceeding Library Archive， 2011， 349.

[8]Srivastava D. A phenomenological model of the rotation dynamics of carbon nanotube gears with laser electric fields [J]. Nanotechnology， 1999， 8（4）： 186.

[9]Requicha A A G. Nanorobots， NEMS， and nanoassembly[J]. Proceedings of the IEEE， 2003， 91（11）： 1922-1933.

[10]Kong L， Guan J， Pumera M. Micro and nanorobots based sensing and biosensing[J]. Current Opinion in Electrochemi stry， 2018， 10174-182.

[11]Wang B， Kra?l P. Chemically tunable nanoscale propellers of liquids[J]. Physical Review Letters， 2007， 98（26）： 266102.

[12]Nelson B J， Dong L. Nanorobotics[M]. Springer Handbook of Nanotechnology， 2010.

[13]Zahir M H， Iwamoto Y， Rahman M M， et al. CaO containing LaCO3OH nanogears and their luminescence and de-NOx properties[J]. Journal of the American Ceramic Society， 2018， 101（12）： 1-15.

[14]Weng Z， Dong L， Yu M， et al. Carbon nanogears and nanotori via combustion flames[J]. Proceedings of the 13th IEEE International Conference on Nanotechnology， 2013， 352-355.

[15]Yu M-F， Lourie O， Dyer M J， et al. Strength and breaking mechanism of multiwalled carbon nanotubes under tensile load[J]. Science， 2000， 287（5453）： 637-640.

[16]Qian D， Wagner G J， Liu W K. Mechanics of carbon nanotubes[J]. Applied Mechanics Reviews， 2002， 55（6）： 495-533.

[17]Terrones M， Banhart F， Grobert N， et al. Molecular junctions by joining single-walled carbon nanotubes[J]. Physical Review Letters， 2002， 89（89）： 075505.

[18]Kim D-H， Huang J， Rao B K， et al. Nonlinear characteristics of pseudo-Y-junction single-walled carbon nanotubes[J]. Journal of Applied Physics， 2006， 99（5）： 056106.

[19]Qin Z， Qin Q-H， Feng X-Q. Mechanical property of carbon nanotubes with intramolecular junctions： Molecular dynamics simulations[J]. Physics Letters A， 2008， 372（44）： 6661-6666.

[20]Bailey S W D， Amanatidis I， Lambert C J. Carbon nanotube electron windmills： a novel design for nanomotors[J]. Physical Review Letters， 2008， 100（25）： 256802.

[21]Kim S Y， Lee I H， Jun S， et al. Coalescence and T-junction formation of carbon nanotubes： Action-derived molecular dynamics simulations[J]. Physical Review B， 2014， 74（19）： 1826-1842.

[22]Guo X， Su J， Guo H. Electric field induced orientation and self-assembly of carbon nanotubes in water[J]. Soft Matter， 2012， 8（4）： 1010-1016.

[23]Menon M， Srivastava D. Carbon nanotube “T junctions”： nanoscale metal-semiconductor-metal contact devices[J]. Physical review letters， 1997， 79（79）： 724-727.

[24]Guo J， Kim K， Lei K W， et al. Ultra-durable rotary micromotors assembled from nanoentities by electric fields [J]. Nanoscale Research Letters， 2015， 7（26）： 11363-11370.

[25]Rinne K F， Gekle S， Bonthuis D J， et al. Nanoscale pumping of water by AC electric fields[J]. Nano Letters， 2012， 12（4）： 1780-1783.

[26]Hess B， Kutzner C， Spoel D V D， et al. GROMACS 4： Algorithms for highly efficient， load-balanced， and scalable molecular simulation[J]. Joural of Chemical Theory and Computation， 2008， 4（3）： 435-447.

[27]Winarto， Takaiwa D， Yamamoto E， et al. Separation of water- ethanol solutions with carbon nanotubes and electric fields[J]. Physical Chemistry Chemical Physics， 2016， 18（48）： 33310- 33319.

[28]Xu Z， Wang C， Sheng N， et al. Manipulation of a neutral and nonpolar nanoparticle in water using a nonuniform electric field[J]. The Journal of Chemical Physics， 2016， 144（1）： 014302.

[29]林介一， 李代禧， 刘宝林， et al. 分子动力学模拟研究干燥阿达木单抗的活性保护[J]. 软件， 2019， 40（06）： 21-26.

[30]Liu L， Patey G N. Simulated conduction rates of water through a （6，6） carbon nanotube strongly depend on bulk properties of the model employed[J]. The Journal of Chemical Physics， 2016， 144（18）： 184502.

[31]李斌， 李蓉， 周蕾. 分布式K-means聚类算法研究与实现[J]. 软件， 2018， （1）： 35-38.

[32]吴江， 孙剑伟. 一种基于云模型的数据预测算法[J]. 软件， 2015， 36（12）： 212-215.

[33]陈向华， 刘可昂. 基于FP-Tree的最大频繁项目集挖掘算法[J]. 软件， 2015， 36（12）： 98-102.

[34]曹盟盟， 姚文斌. 基于改进粒子群算法的虚拟机放置算法[J]. 软件， 2015， 36（12）： 89-92.

[35]唐漢香， 刘宇畅， 唐一超. 基于局部搜索的Memetic差分演化算法[J]. 软件， 2015， 36（10）： 13-16.

[36]董晴， 宋威. 基于粒子群优化的深度神经网络分类算法[J]. 传感器与微系统， 2017， 36（09）： 143-146+150.

[37]任关友， 王昕， 李英娜， et al. 基于粒子群优化神经网络算法的用户防窃电研究[J]. 软件， 2017， 38（08）： 215-219.

[38]傅德胜， 经正俊. 基于PCA-LDA和KNN-SMO的数据碎片分类识别算法[J]. 软件， 2015， 07（07）： 21-25.

[39]Darden T， York D， Pedersen L. Particle mesh ewald： an N·log（N） method for ewald sums in large systems[J]. The Journal of Chemical Physics， 1993， 98（12）： 10089-10092.