复合多铁链的磁电耦合行为与外场调控∗

黄颖妆 齐岩 杜安 刘佳宏 艾传韡戴海燕 张小丽 黄雨嫣

1)(大连民族大学物理与材料工程学院,大连 116600)

2)(东北大学物理系,沈阳 110819)

(2018年8月19日收到;2018年10月15日收到修改稿)

对含有界面磁电耦合的有限长铁电-铁磁多铁链体系进行了研究,基于矢量离散化思想,构建了描述其磁电性质的微观海森伯模型.利用传递矩阵方法获得了磁化强度、电极化强度、磁电化率等关键热力学量的解析表达式,重点探讨了界面磁电耦合、外场以及单离子各向异性对体系磁电耦合行为的影响和调控.研究结果表明,界面磁电耦合对体系的磁化强度和电极化强度均起促进作用.电场驱动下的电致磁电化率具有更强的磁电关联效应,预示着外电场能够有效地调控体系的磁性行为.而在磁致磁电化率中观察到的低温峰主要源于外磁场的诱导.此外,在高电场作用下体系比热容还呈现出有趣的三峰结构,这种三峰结构是自旋态的热激发以及电偶极矩的电场和温度共同激发导致的.

1 引 言

多铁性材料能同时展现出多种铁性序,包括磁性序、电性序及弹性序,并且这些铁性序间存在耦合效应,使得多铁性材料在自旋电子器件、固态变压器、高灵敏度磁场传感器等方面极具应用潜力,已成为国内外热点研究课题[1−3].尤其是磁电多铁性材料,铁电序和铁磁(反铁磁)序共存并相互耦合,能够进行磁电间的相互调控,因而具有非常广阔的应用前景[4,5].

近期实验研究表明,已经能够通过人工合成具有纳米级异质结的铁电-铁磁复合多铁材料.该类材料有望弥补单相多铁性材料在室温应用方面的不足,并为材料磁电性能的改良提供新思路[6,7].典型的代表为由铁电材料BaTiO3和铁磁材料Fe构成的复合铁电/铁磁体系.2006年,Duan等[7]利用第一原理计算预测了Fe/BTiO3多层体系中磁电效应.2007年,Sahoo等[8]首次在实验上成功合成了该材料,并指出在室温条件下,外电场可以驱动该体系铁层的磁化强度发生变化.这一重要发现引起了人们对其磁电调控行为的深入研究.Horley等[9]利用Landau-Lifshits-Gilbert和Ginzburg-Landau动力学理论,研究指出频率为0.5—12 GHz谐波电场能使复合多铁链的磁化强度发生完全翻转,并且该翻转行为对界面处的磁电耦合强度高度敏感.Chotorlishvili等[10]通过解析和数值计算指出界面处的磁电耦合决定了初始铁电局域模式向铁磁信号的转变,并明确了由铁电转变为铁磁信号的初始条件.Rondinelli等[11]研究指出其多铁性耦合源于铁电部分极化引起的铁电/铁磁界面自旋极化电子或空穴的积累.在金属/绝缘体界面处,极化电荷的屏蔽改变了铁电极化方向,从而导致表面磁化强度的线性改变.Cai等[12]研究了具有铁磁/铁电/金属超晶格结构体系的磁电效应,并预测了电场对该体系磁化强度的有效调控,并指出铁电/铁磁异质结中的磁电耦合效应不依赖于特殊的化学或物理键,将在多铁性材料应用中发挥重要作用.Sirker[13]利用近邻铁磁耦合、次近邻反铁磁耦合的海森伯模型对多铁自旋链材料的热力学性质进行了细致研究,指出无公度自旋间关联的效应对铁电性质的影响至关重要.Ding等[14]基于多体格林函数理论对一维有机量子磁体中的自旋-晶格耦合驱动的铁电相变行为进行了研究,获得了与实验定量相符的结果,详细探讨体系的磁电耦合行为.Paglan等[15]研究了纳米结构多铁复合材料BaTiO3/Fe的非线性动力学,并利用界面磁电耦合效应通过铁电极化强度激发获得了长时间稳定的磁激发.这些取得的重要成果对通过电场脉冲写入的复合多铁存储元件的开发具有重要的借鉴意义与推动作用.

目前,对该类材料的研究主要集中在外场驱动的磁化强度和电极化强度的动力学行为研究[16−19],而对其热力学性质的相关研究还未见报道.因此本文针对具有界面磁电耦合的多铁链体系,利用理论和数值解析手段对体系的磁电热力学性质进行细致研究,进一步深化其内部微观作用机制的认知和理解.

2 理论模型与方法

针对具有界面磁电耦合的多铁链体系,考虑由局域磁矩和电偶极矩构成的有限长复合多铁链体系,示意图如图1所示.考虑铁磁和铁电部分的交换作用仅限于界面处的第一个位置,体系的总能量由三部分组成[10]:

铁磁部分的能量为

而铁电部分能量为

界面磁电耦合能表示为

式中电偶极矩pj和磁矩Si均为三维经典单位矢量;E和H分别为外电场和外磁场,均施加在z轴方向;JE表示铁电部分近邻粒子间的交换耦合;Sn和p1分别表示界面处粒子的磁矩和电偶极矩,如图1所示;JM=1.0表示近邻磁性粒子间的交换耦合;JE=1.0表示近邻电偶极子间的交换耦合;JME=0.5表示电磁粒子间的交换耦合强度;D=0.2表示磁性粒子具有的单离子各向异性;K1=−0.5,K2=0.25为朗道系数,用于描述铁电和顺电的二级相变[20,21].

图1 磁电复合多铁链示意图Fig.1.Schematic diagram of a magnetoelectric composite multiferroic chain.

为了求解表征体系磁电性质的关键物理量,首先要给出体系的配分函数:

式中求和遍及自旋和电偶极矩变量的所有构型,β=1/(kBT),kB为玻尔兹曼常数并取其值为1,T为绝对温度;Hi表示哈密顿量H第i个结构单元的能量本征值.基于配分函数,体系的平均自由能可表示为

式中F为体系总自由能,N为体系所包含的总粒子数.一旦获得体系的自由能,在此基础上通过对其求偏导,便可得到磁化强度mz、电极化强度pz、比热容C以及磁电极化率χme等关键物理量解析表达式.根据统计物理,以上关键磁电量可表示为[22]

为了方便讨论,本文选取JM作为约化单位,引进一套无量纲参数jE=JE/JM,jME=JME/JM,k1=K1/JM,k2=K2/JM,h=H/JM,hE=E/JM,δ=D/JM和t=T/JM.

但总体而言,该矢量模型在数学上不可积,获得其热力学性质是一个非常难处理的问题.为此,本文基于自旋矢量离散化的思想对该模型进行近似处理,即在半径为1的矢量球上均匀取362个点(图2),作为自旋态和极化态构建经典磁电矢量模型.在此基础上,利用传递矩阵方法完成具体磁电参数解析表达式的推导,其中传递矩阵方法遵循标准流程[23],这里不再呈现繁琐的公式推导.为了验证该思路的正确及有效性,本文基于该离散化矢量模型计算了零场下一维海森伯模型的磁比热容,并与Fisher[24]得到的严格解进行了比较,如图3所示.计算结果重现了磁比热容在温度接近零时趋近于1的主要特征,而且可以看到整体的变化趋势也基本一致,除了转变温度和严格解间存在一定偏差,这主要是由自旋态取值有限所致,表明了该近似方法的合理性和可行性.

图2 单位矢量球面均匀分布362个点Fig.2.362 points uniformly distributed on the unit vector sphere.

图3 零场下,经典海森伯自旋链体系的比热容随温度的变化Fig.3.Zero-field specific heat versus temperature for a classical Heisenberg chain.

3 计算结果与讨论

在具体分析体系磁电行为前,首先检查了尺寸效应的影响.图4给出了外磁场作用下,不同铁电和铁磁链长度对应的磁化强度和电极化强度随温度的变化情况.从图4可以很直观地看到,当铁电和铁磁的链长各达到或超过50时,尺寸效应所带来的影响几乎忽略不计.因此在接下来的计算分析中,体系的总粒子数N取值为100,铁电和铁磁链长各为50.

图4 外磁场作用下,不同链长体系的(a)磁化强度和(b)电极化强度随温度变化情况Fig.4.Temperature dependence of(a)magnetization and(b)electric polarization for different chain length under an external magnetic field.

图5 不同外磁场下(a)磁化强度和(b)电极化强度随温度的变化;不同外电场下(c)磁化强度和(d)电极化强度随温度的变化Fig.5.Temperature dependence of(a)magnetization and(b)electric polarization for different magnetic field;temperature dependence of(c)magnetization and(d)electric polarization for different electric field.

图5给出了不同外磁场和外电场时,磁电复合多铁链体系中磁化强度mz和电极化强度pz随温度的变化.众所周知,在有限温度下,一维铁磁铁电体系不存在长程有序,因此零场磁化强度和电极化强度均为零[25,26].考虑体系具有弱单离子各向异性下,本文解析计算(图像没有展示)重现了该结果验证了模型的合理性和可行性.从图5可发现,由于近邻自旋(电偶极矩)间的铁磁(铁电)交换耦合,即使在弱外磁场(外电场)作用下,mz(pz)在温度接近零时也趋近饱和,但因体系的维度较低、对温度热涨落的抵抗能力弱,随温度的升高mz(pz)很快瓦解.观察图5(b)和图5(c)可以看出,虽然磁场(电场)的改变对pz(mz)的影响不是很显著,但极低温下磁电间的关联仍然比较强,具体表现为在较小外磁场(电场)驱动下便在极低温下达到极值,表明磁电界面耦合效应能够有效调控铁磁-铁电异质结体系的多铁动力学行为,与早期发表的结果相符合[16−19].总体而言,对于铁电-铁磁构成的复合磁电体系,外磁场和外电场对mz和pz始终起着增强作用[27,28],与通常磁致多铁体系中的铁电极化对外磁场的响应不同[29,30],其中磁场(电场)对铁磁链(铁电链)部分的促进作用尤为显著(图5(a)和图5(d)),这主要是由于该复合多铁链体系仅在铁电和铁磁链界面连接处存在耦合,在温度热涨落的影响下,整体磁电关联很容易受到破坏,从而导致外磁场(电场)对pz(mz)的增强作用不突出.鉴于此,为了更加直观地刻画体系的磁电耦合效应,接下来将重点探讨界面衔接处磁矩、电偶极矩间的关联函数对外场响应,即界面处的磁电极化率随温度变化情况,如图6所示.

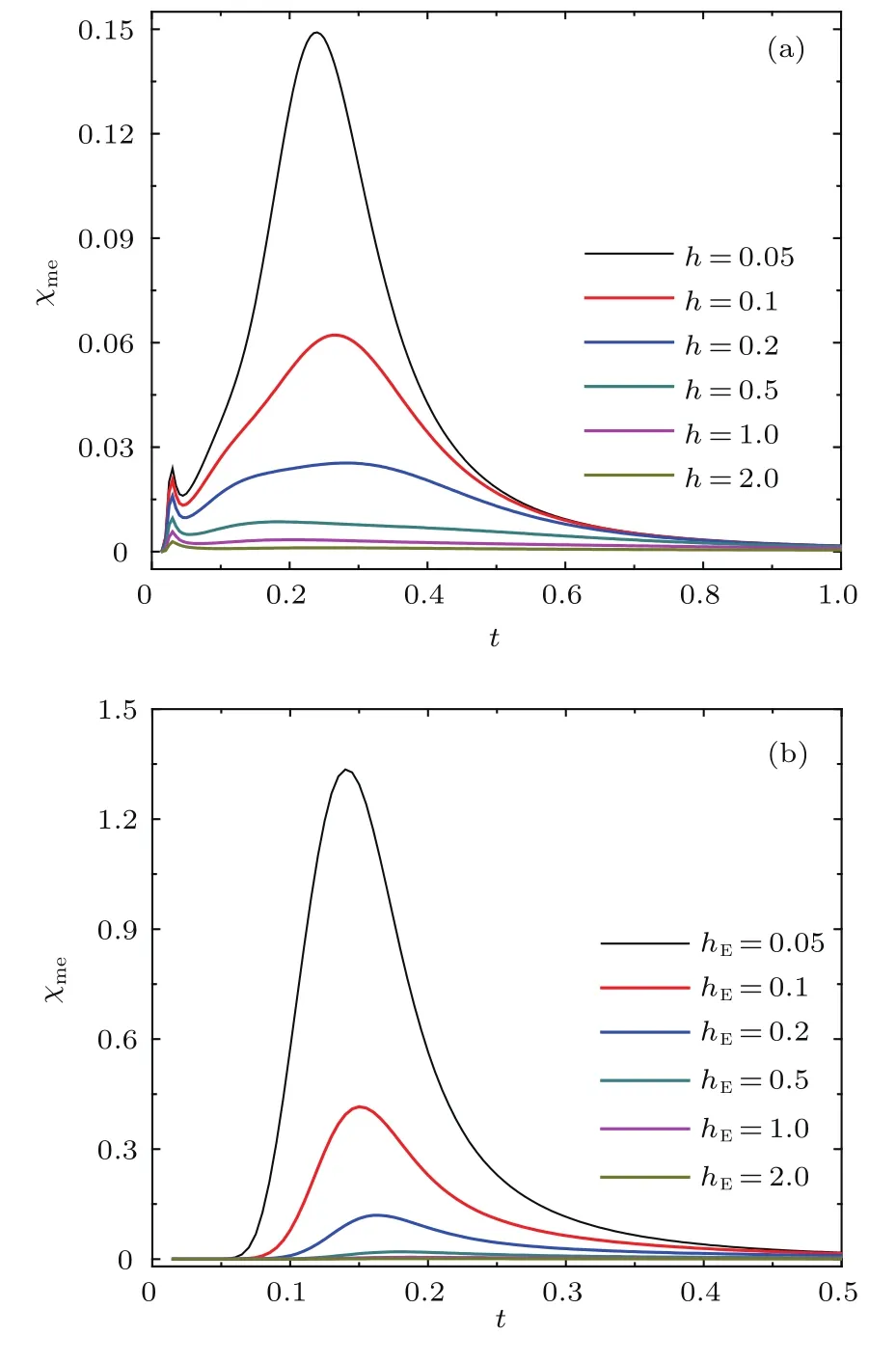
图6 (a)磁致磁电化率和(b)电致磁电化率随温度的变化Fig.6.Temperature dependence of magnetoelectric susceptibility driven by different(a)magnetic fields and(b)electric fields,respectively.

从图6(a)可以看到,体系的磁致磁电化率呈现出新颖的双峰结构,具体表现为极低温的小尖峰和高温的圆峰,并且峰值随外磁场的增加而减小,尤其是高温峰表现得极为明显,迅速下降并在磁场达到与近邻交换耦合作用相当时趋近于零,与自旋S=1的一维海森伯铁磁体磁化率行为相似[31−33].表明体系的磁介电响应随磁场的增加而削弱,其中极低温峰的存在是外磁场和温度共同激发的结果[25,26].类似地,在外电场作用下,电致磁电化率展现出相同的变化趋势,如图6(b)所示,只不过表现为单峰结构.实质上,磁致磁电化率(电致磁电化率)峰值受到抑制的行为主要是因为外场的增强极大地削弱了自旋和电偶极矩的涨落效应.在外场作用下,自旋和电偶极矩的取向越来越趋向外场方向,从而呈现出峰值降低的变化趋势.对比图6(a)和图6(b),不难发现与磁致磁电化率相比,电致磁电化率的峰值高出很多,相应的界面磁电关联效应表现得更加强烈,预示着电场对体系磁性行为的有效调控,该结论与Venkataiah等[34]在异质结Fe/BaTiO3中观察到的现象相符合.

图7给出了不同单离子各向异性作用下,体系的磁致磁电化率随温度的变化情况.可以看到在不考虑单离子各向异性的情况下,磁致磁电化率仍然表现为双峰结构,表明极低温峰是磁场和温度共同作用下诱导的.当单离子各向异性存在时,磁致磁电化率低温和高温峰受到了明显的抑制作用,峰值急剧下降并随其增强而呈现继续降低的趋势.这主要由于沿z方向施加的单离子各向异性使得磁性粒子的朝向更加趋向外磁场方向,同时界面处与磁性离子耦合的电偶极矩也会随之扭转方向,从而削弱了自旋和电偶极矩间的关联效应.

图7 不同单离子各向异性下,磁致磁电化率随温度的变化Fig.7.Temperature dependences of magnetoelectric susceptibility driven by magnetic field for different single anisotropies.

图8 显示了外磁场对体系比热容的影响.从图8可以看到,在没有外磁场作用下,体系比热容在温度趋近于零时呈现出有限值并随温度的升高达到极大值,呈现出单峰结构.当对体系施加较小外磁场h=0.05时,比热容由单峰转变为双峰结构并向高温区发生了移动,但峰值受到了一定抑制作用.当继续增加外磁场,比热容的低温峰和高温峰同时加宽并继续向高温区移动,整体的峰值继续下降,其中高温峰值下降得比较迅速.当磁场增加到h=1.0时,高温峰已下降到低温峰以下并表现为非常宽阔的曼陀峰.继续加大磁场,此时高温峰与低温峰合并在一起,比热容恢复为单峰结构.整体来看,磁场增强有利于体系抵抗温度升高引起的热涨落影响.为了揭示和理解比热容复杂变化行为的本质,依据体系哈密顿量的构成,将比热容分成三部分,分别对应于铁磁、铁电以及界面磁电耦合能的贡献,并用符号∂HM/∂T,∂HE/∂T和∂HC/∂T表示,具体计算结果如图9所示.

图8 不同外磁场下,比热容随温度的变化Fig.8.Specific heat versus temperature under different external magnetic fields.

铁电部分如图9(b)所示,正如我们所预期的,体系仅在界面处存在磁电耦合,因此纯铁电部分贡献的比热容对外磁场是完全没有响应的,展现出类似经典海森伯自旋体系的比热容行为[24],即在极低温下比热容并不是趋近于零,而是在温度区间0—0.5范围内几乎维持在一定值并随温度的增加逐渐瓦解.若将该部分比热容与纯铁磁贡献的比热容相叠加(图9(a)),显而易见除整体数值得到提升外,比热容将继续维持图9(a)的变化趋势.与图8对比,可以看到这与体系总比热容变化情况相一致.表明在外磁场作用下,体系铁磁部分对外磁场和温度的响应占主导.图9(c)为界面磁电耦合部分贡献的比热容,与前两者相比数值非常小,虽随外磁场的增强而增大,但对体系总比热容的变化趋势影响并不大,几乎可以忽略不计.因此由以上可推断体系总比热容的双峰结构是磁性粒子的交换耦合能、单离子各向异性能、塞曼能以及温度热涨落间相互竞争的结果.因为单离子各向异性的存在会导致体系呈现易磁化轴,而外磁场在一定程度上增强了单离子各向异性效应,进而对比热容低温行为产生了强烈的影响,尤其是铁磁自旋链情况,在温度热涨落作用下,xy平面内与z轴方向的局域自旋激发态产生相互竞争,从而导致比热容呈现出双峰结构[35].

图9 不同外磁场下,(a)∂HM/∂T,(b)∂HE/∂T和(c)∂HC/∂T 随温度的变化Fig.9.Temperature dependences of(a) ∂HM/∂T,(b)∂HE/∂T and(c)∂HC/∂T under different external magnetic fields.

图10显示了外电场对体系比热容的影响.为了清晰地显示比热容变化的细节,本文给出了比热容随温度的lg指数变化情况.可以看到,在外电场调控下,比热容的变化趋势极其复杂,并呈现出奇特的三峰结构,低温峰值随电场的增强呈现出先上升后下降的变化趋势.为了揭示比热容三峰结构来源,同样地,图11具体给出三部分能量对比热容的贡献及其对外电场的响应.

图10 不同外电场下,比热容随温度的变化Fig.10.Specific heat versus temperature under several external electric fields.

图11 (b)显示了不同外电场作用下,体系铁电部分能量所贡献的比热容随温度的变化情况.可以看到,在外电场作用下,该部分比热容始终呈现出双峰结构,具体表现为低温的高峰和高温的宽矮峰,并且两峰对应的转变温度均随外电场的增强向高温区发生了移动,同时伴随着峰宽加宽.其中高温峰受到了明显的增强作用,峰值增大,低温峰则受到微弱的抑制作用.对比图10结果,可知高电场下比热容三峰结构不单一来源于铁电部分贡献,为此结合图11(a)做进一步分析.从图11(a)可以看到,铁磁部分能量所贡献的比热容在低温下保持较大的峰值,仍是总比热容的重要来源之一.为明确铁磁部分对高场下比热容三峰的具体贡献,对电场hE=2.0时,图11(a)中峰值对应的转变温度进行了标识,为0.17,这与图10三峰结构的极低温峰温度转变点相符合,表明高电场情况下比热容三峰结构中的极低温峰对应于自旋态的热激发.同样地,对图11(b)高场峰温度转变点标识分别为0.52和1.35,与图10三峰结构中另外两峰位置相符合,说明中高温两峰对应于铁电偶极矩的电场和温度激发.同样地,遵循相同的思路对于低电场的比热容情况进行分析.观察图11(a)和图11(b),可看到铁磁和铁电能量贡献的比热容在低温区转变温度非常接近,基本重合在一起,铁磁转变峰不突出,因而使得体系总比热容仅仅表现出双峰结构.此外,对比图10和图11(c)发现,改变外电场,体系总比热容低温峰值先增加后减小的复杂变化行为主要由界面耦合能决定的.

图11 不同外电场下,(a)∂HM/∂T,(b)∂HE/∂T和(c)∂HC/∂T 随温度的变化Fig.11.Temperature dependences of(a) ∂HM/∂T,(b) ∂HE/∂T and(c) ∂HC/∂T under different external electric fields.

4 结 论

本文对具有界面耦合的有限长复合多铁链体系的磁电耦合行为及外场调控机制进行了研究.构建了微观海森伯磁电模型,基于矢量离散化近似思想结合传递矩阵解析手段,对反映体系关键磁电性质的物理量进行了求解,具体包括磁化强度、电极化强度、磁电化率及磁比热容.研究结果显示:在较小外磁场(电场)驱动下,电极化强度(磁化强度)便可在极低温下达到极值,表明磁电界面耦合效应能够有效调控该异质结体系的多铁动力学行为.在此基础上,探讨了界面衔接处磁矩、电偶极矩间的关联函数对外场和界面耦合的响应,计算结果表明电致磁电化率具有更强的磁电关联效应,外磁场(电场)以及磁性粒子的单离子各向异性对整体磁电化率均起抑制作用.最后对不同外场参数下的比热容行为进行了细致分析.在高电场驱动下,观察到体系比热容奇特的三峰结构,该行为是由自旋态的热激发以及电偶极矩的电场和温度共同激发导致的.