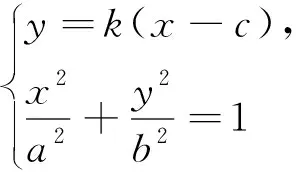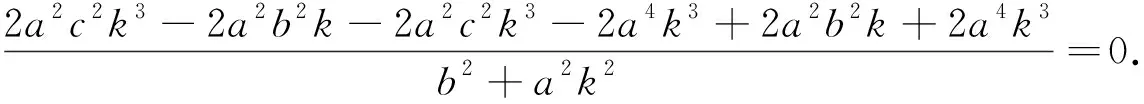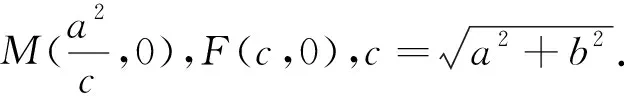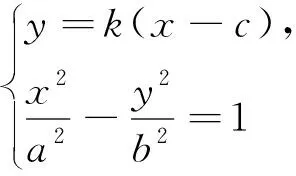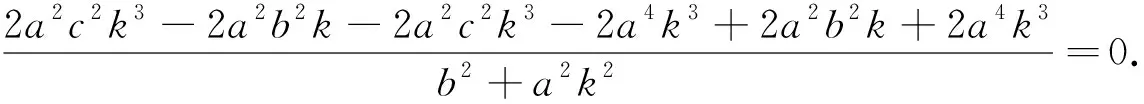圆锥曲线题中的等角问题

山东省聊城大学数学科学学院 (252000)

张 鑫 于兴江

新课标全国Ⅰ卷的圆锥曲线部分难度变化不大，但稳中有变.本文以文科卷第20题及理科卷第19题为例，利用几何画板探究了直线与圆锥曲线相交时的等角问题.

2018年全国高考(文)Ⅰ卷第20题：设抛物线C:y2=2x，点A(2,0),B(-2,0)，过点A的直线l与C交于M，N两点.

(1)设l与x轴垂直时，求直线BM的方程；

(2)证明：∠ABM=∠ABN.

(1)设l与x轴垂直时，求直线BM的方程；

(2)设O为坐标原点，则∠OMA=∠OMB.

我们利用几何画板探究得到.

定理1 设抛物线C:y2=2px(p>0)，点A(m,0),B(-m,0),m>0,过点A的直线l与C交于M,N两点，则∠ABM=∠ABN.

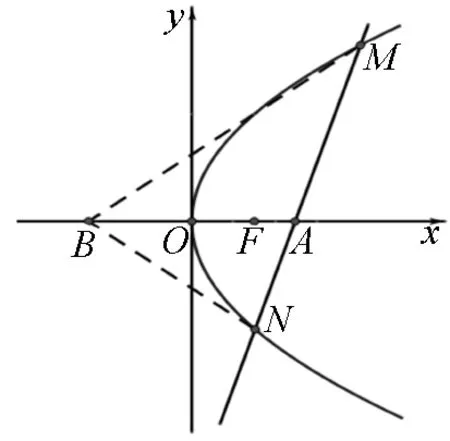
图1

证明:当l与x轴垂直时，AB为MN的垂直平分线，所以∠ABM=∠ABN.当l与x轴不垂直时，设l的方程为y=k(x-m)(k≠0),M(x1,y1),N(x2,y2),则x1>0,x2>0.

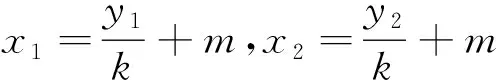
综上所述，∠ABM=∠ABN.

注：2018年全国Ⅰ卷文科卷第20题中，当p=1,m=2时，经过点A的直线l与抛物线C交于M,N两点，则∠ABM=∠ABN.

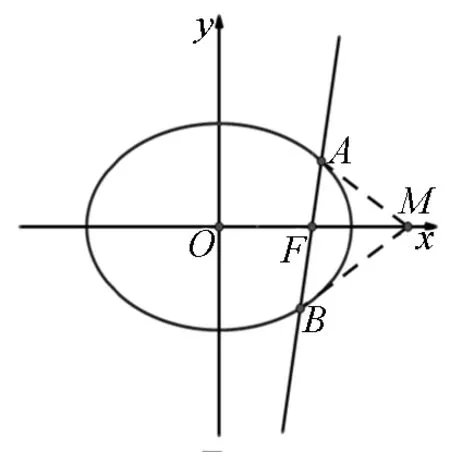
图2

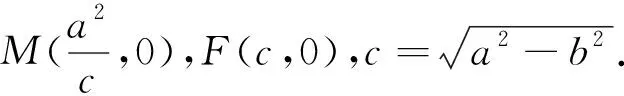
当l与x轴重合时，∠OMA=∠OMB=0°.

当l与x轴垂直时，OM为AB的垂直平分线，所以∠OMA=∠OMB.

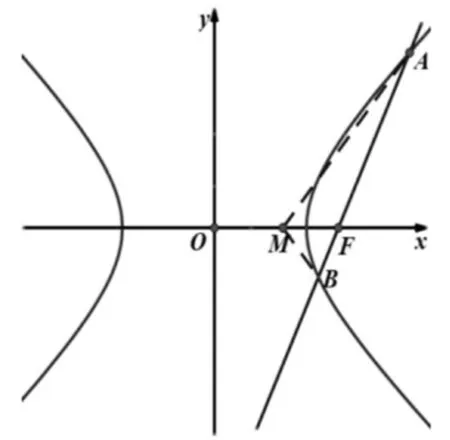
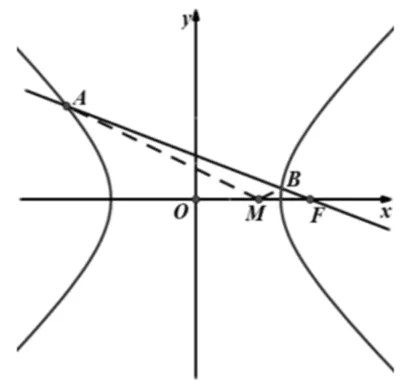
当l与x轴既不重合也不垂直时，设l方程为y=k(x-c)(k≠0),A(x1,y1),B(x2,y2),则-a

将直线方程与椭圆方程联立,得

将y1=k(x1-c),y2=k(x2-c)及x1+x2,x1x2的表达式代入(1)式中分子，可得

综上所述，OMA=∠OMB.

注：2018年全国Ⅰ卷理科卷第19题中，当a2=2,b2=1时，经过右焦点F的直线l与椭圆C交于A,B两点，点M的坐标为(2,0)，设O为坐标原点，则∠OMA=∠OMB.

图3

当l与x轴重合时，∠OMA=∠OMB=180°.

当l与x轴垂直时，OM为AB的垂直平分线，所以OMA=∠OMB.

当l与x轴既不重合也不垂直时，设l的方程为y=k(x-c)(k≠0),A(x1,y1),B(x2,y2),则x1>a,x2>a.

将直线方程与双曲线方程联立

将y1=k(x1-c),y2=k(x2-c)及x1+x2,

综上所述，OMA=∠OMB.

图4

本文以探究圆锥曲线中等角问题为例，力求培养学生的创新意识及探索新知能力.