椭圆、双曲线的一个性质及其应用

宁夏彭阳县第一中学 (756599)

杨莉莉

在圆锥曲线的教学与学习中，我们容易得到椭圆、双曲线的如下两个性质：

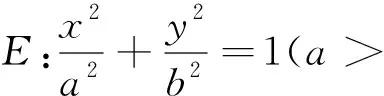
图1

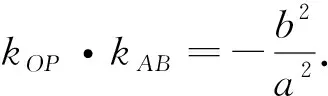
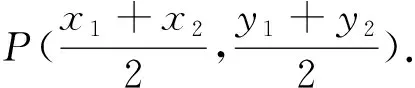
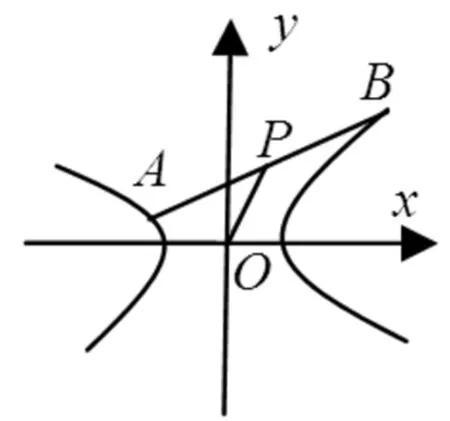
图2

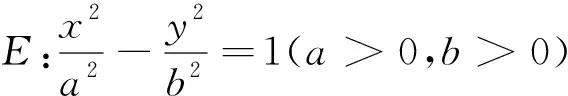
性质2的证明同性质1.此略.

我们发现用这两个性质求解椭圆、双曲线涉及到中点弦、弦中点的问题，具有思路简洁、计算量小的特点，下面举例予以展示.

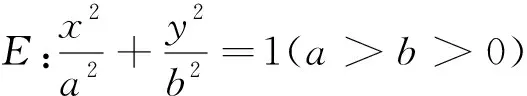
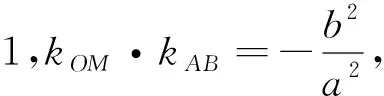
又a2-b2=9，所以得b2=9，a2=18.故选D.

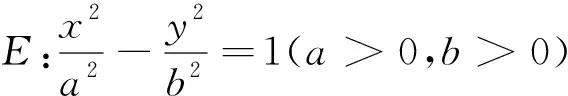
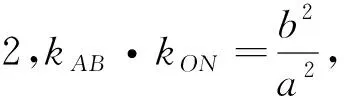
例3 (2015新课标卷理20题)已知椭圆C:9x2+y2=m2(m>0)，直线l不过原点O且不平行于坐标轴，l与C有两个交点A、B，线段AB的中点为M.

(1)证明：直线OM的斜率与直线l的斜率的乘积为定值；(2)略.

解:(1)的证明方法同性质1，得到直线OM的斜率与直线l的斜率的乘积为-9(定值).

(1)求C的离心率；(2)略.

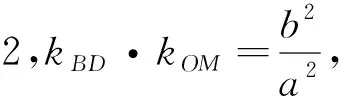
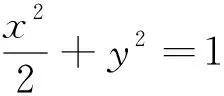
(1)求实数m的取值范围；(2)略.

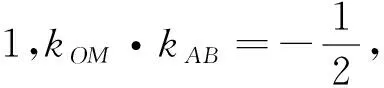
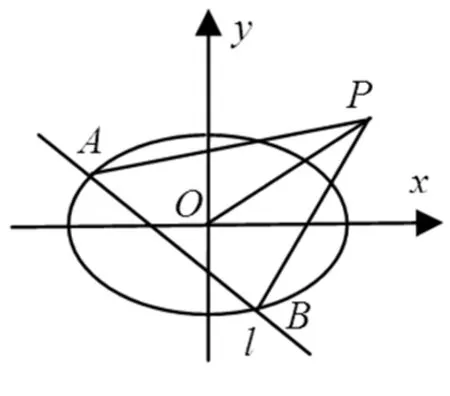
图3

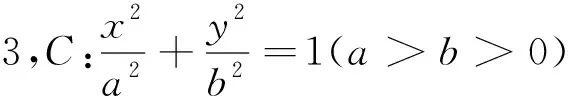
(1)求椭圆C的方程；

(2)求ΔABP的面积取得最大时直线l的方程.

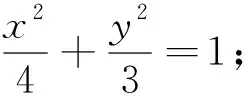
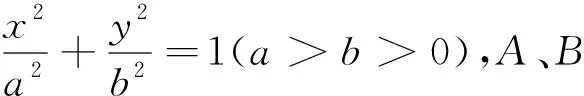
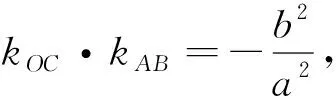
在数学教学中，特别是数学解题教学中，我们要引导学生善于发现问题、总结规律、提炼结论，并会用新的结论简洁的解答数学问题.