突破运算瓶颈,落实核心素养*
——对一道解析几何模考题解法探究的思考
江苏省扬中高级中学 (212200)
高忠冉
教育部《普通高中数学课程标准(2017)》对核心素养作了具体的阐述:数学学科核心素养是育人价值的集中体现,是学生通过学科学习而逐步形成的正确价值观念、必备品格和关键能力.数学学科核心素养是数学课程标准的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现,是在数学学习和应用的过程中逐步形成和发展的.数学学科核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.“核心素养”是当今教育界谈论的热点话题,如何在课堂教学中落实是当前数学教育工作者关注的焦点,也是数学教师面临的新课题和挑战.
数学运算贯穿整个高中数学教学,是学生能否取得好成绩的关键能力之一.解析几何作为培养运算能力的沃土,是落实数学运算核心素养的最佳载体.下面以一道模考题的解法探究为例,浅谈在解析几何教学中如何突破运算瓶颈,落实核心素养.
一、试题呈现
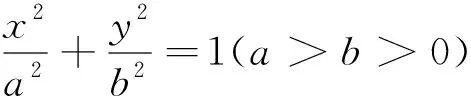
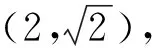
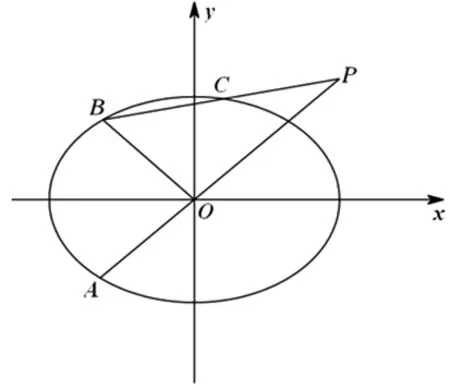
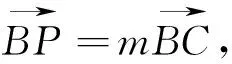
第二问主要考查圆锥曲线中的定值问题,是近年高考的热点题型,其求解思路非常明确,一是根据向量关系求出点C的坐标,将点C代入椭圆方程求m的值;二是利用直线PB与椭圆相交求出点C的坐标,再根据向量关系求m的值.
二、解法探究
解法1:直接选择A,B的坐标为参数.
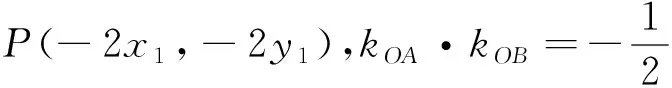
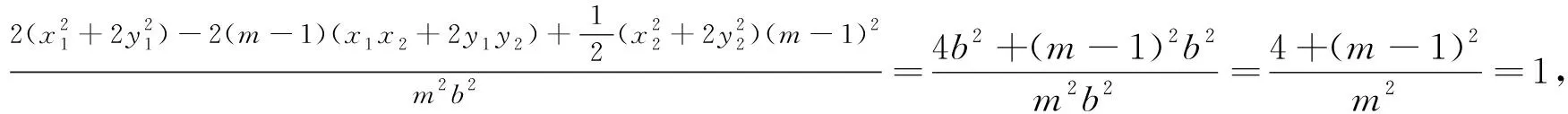
点评:将点C的坐标用x1,y1,x2,y2来表示,形式非常对称,再代入椭圆方程整体消参,达到了快速、简捷的解题效果,一气呵成,妙不可言!
解法2:三角代换,选择角度作为参数.
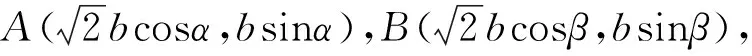
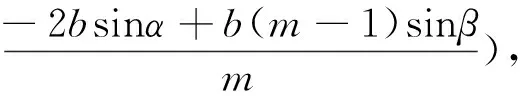
点评:三角代换也是十分有效的方法.将A,B,C三点的坐标用角α,β来表示,代入椭圆方程后利用三角恒等式sin2α+cos2α=1便可轻松化简,与解法1有异曲同工之妙.
解法3:选择点A的坐标为参数.
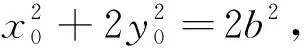
将点C代入椭圆方程得
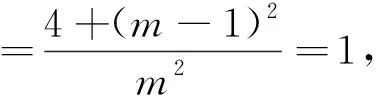
点评:因直线OB经过原点,故求交点B的坐标比较容易.
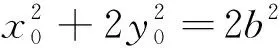
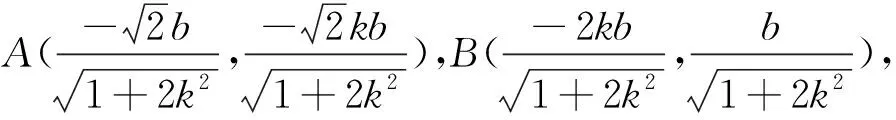
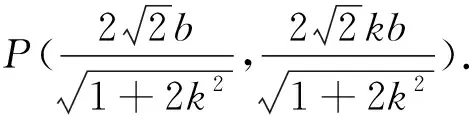
将点C代入椭圆方程得
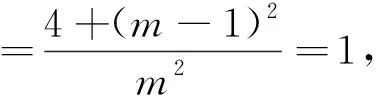
点评:“斜率”作为直线与圆锥曲线相交问题中的重要参数备受学生的青睐,其优势是参数唯一,目标明确.但从解题过程不难发现选择“斜率”作为参数时难点也非常突出,一是求点C的坐标运算量较大,二是其坐标复杂(含根式),导致化简极易出错.由此可见,合理选择参数对控制运算量的大小有着至关重要的影响.
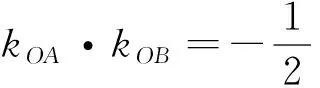
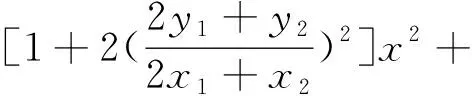
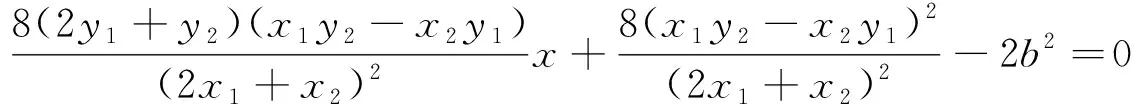
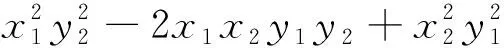
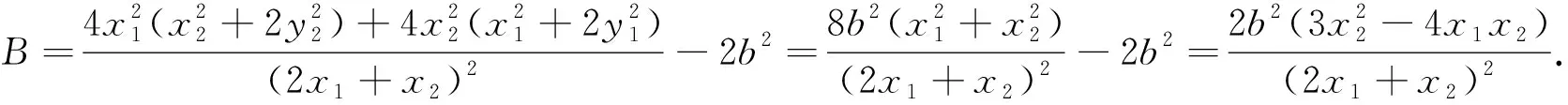
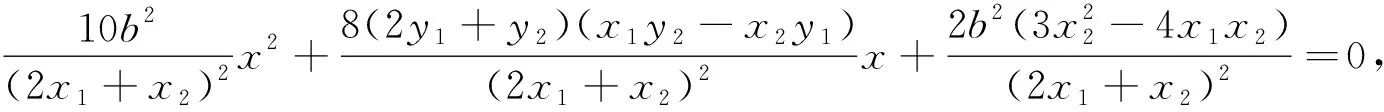
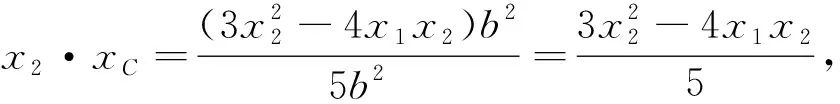
点评:此法思路比较直接,但对学生的运算能力要求非常高,突破运算的关键是化简“B”,只要攻下这一堡垒,下面便柳暗花明,迎刃而解了.
三、教学思考
数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.主要包括:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果.基于本题的解法探究,对解析几何的运算教学,笔者有以下几点思考.
1.理解思想方法产生的本质,提高选择能力
无论是“坐标”还是“直线的斜率”,教师都应当将选择的原因分析透彻,讲清来龙去脉,唯有如此,学生才能知其然而更知其所以然,从而提高选择能力,找到最佳方案,力促高效解题.
2.从理解算理的维度化简运算,提升运算能力
《课标》在解读“运算能力”时强调“应当重视学生是否理解了运算的道理,是否能准确地得出运算的结果,而不是单纯地看运算的速度”,可见算理才是运算能力的核心.解法1中,根据向量关系,将点C用A,B两点的坐标表示后,显然式子“x1x2+2y1y2=0”和“x2+2y2=2b2”是进行化简运算的关键隐含条件,集中体现了“设而不求”这一解析几何的基本思想.在解法5化简系数“A”和“B”的过程中,“设而不求”体现得淋漓尽致,事实上,它也反过来指导系数“A”和“B”的变形与化简方向,两者可以说相辅相成,相得益彰.学生若没有理解这一重要算理,很难想象能化简“A”和“B”.
教学中教师要引导学生对算理进行深入的研究,帮助和指导学生应用已有的知识感悟其中的算理.学生只有对算理有了深刻的理解,才能快速找到运算的方法进行正确迅速地运算,从而真正达到“想得多算得快、算得少”的境界.
3.从数学育人的维度塑造品格,落实核心素养
从应试角度而言解法5是不可取的,但它对培养学生的运算能力和塑造学生的思维品质具有很高的价值.在高三复习阶段,尤其一轮复习是提高学生运算能力和培养自信心的最佳时机.“纸上得来终觉浅,绝知此事要躬行”.在遇到运算量较大的解析几何问题时切不可错失良机,教师应当勇于带领学生突破运算瓶颈,任性算到底,没有“任性”何来“韧性”?解法5中的运算过程完全可以用“惊心动魄”来形容,当学生通过自身的努力化简方程①,最终解出点C的坐标时,这个“惊心动魄”的过程对学生内心的震撼是可想而知的,对磨练学生的毅力,塑造学生坚忍不拔的品格,提升学生的自信,无疑有着不可估量的作用,是任何语言难以企及的.
教育的根本任务是育人.著名数学教育家波利亚说过:“如果学生在学校里没有机会尝尽为求解而奋斗的喜怒哀乐,那么他的数学教育就在最重要的地方失败了.”数学为磨练学生的意志和提高耐挫力提供了绝好的平台,意志品质水平的高低与数学成绩的优劣有着极为密切的内在联系.高三同学要在体验挫折和失败的过程中,形成百折不挠的良好心理素质,以应对高考这样的重要考试,这既是高考的要求也是今后人生发展的需要,也只有这样才能真正完成落实数学学科核心素养的目标和立德树人的根本任务.

