基于小波变换与SVD的水电机组振动信号特征提取研究

刘 东，王 昕，黄建荧，胡 晓，肖志怀

(1.武汉大学动力与机械学院，武汉 430072；2.福建水口发电集团有限公司，福州 350004)

0 引 言

保障水电机组安全稳定运行对于提高电力系统的稳定性具有重要意义，对水电机组进行准确有效的状态监测与故障诊断必不可少，信号特征提取过程是诊断的前提与基础[1]。为保障故障诊断结果的准确度与可信度，通常选取尽可能多的样本建立故障特征集。大量数据样本将延长运算时间，对诊断系统网络收敛造成一定影响。特征提取的核心是在保证诊断准确度的前提下尽量减少与故障诊断无关的信息，提取有效的核心参数。

水电机组信号特征提取方法众多，例如傅里叶变换、小波变换、经验模态分解(Empirical Mode Decomposition，EMD)、自适应多小波变换等。黄镔[2]等人利用细化的FFT方法，对水电机组的振动信号的频谱进行精细化分析。朱文龙[3]等人提出了一种结合独立分量分析(ICA)和经验模态分解(EMD)的ICA-EMD方法，用于提取水电机组振动信号特征。卢娜[4]研究分析基于综合检测指数(SDI)的自适应多小波变换方法以提取机组的振动信号特征。对于局部特性显著的信号，傅里叶分析方法具有一定局限性；使用EMD方法批量处理数据时，IMF分量个数不确定，易产生端点效应以及模式混合等问题[5]；自适应多小波方法应用于水电机组实际振动数据分析时，存在后台处理复杂度、计算速度的实用性问题。

奇异值分解(Singular Value Decomposition，SVD)方法作为一种现代数学工具，其本质是一种矩阵分解。SVD方法从数据矩阵变换来处理分析信号，不同于傅里叶分析、小波分析中时频域转换的思想，但具有类似的信号分析能力。由于SVD方法稳定简捷，该方法逐渐应用于各实际工程领域。杨宇[6]等人提出结合EMD与SVD方法，用于滚动轴承的振动信号故障特征量的提取，此方法对于诊断滚动轴承故障成功有效。Muruganatham[7]等人提出了一种基于SVD的奇异谱分析法(SSA)，用于去除轴承振动信号强烈的背景噪声，准确提取其振动信号的特征。基于SVD方法用于水电机组信号分析领域的研究案例并不常见，本文提出结合小波变换与SVD的特征提取方法用于处理水电机组振动信号。运用小波变换得到信号的小波分解系数，对系数进行单支差值重构后构成SVD的输入矩阵，提取奇异值(SV)得到水电机组振动信号特征向量，最后通过分类方法验证该特征提取方法的可信度。

1 小波变换理论

1.1 离散小波变换

WTf(m,κ)=〈f(t),ψm,κ(t)〉=

(1)

式中变换结果WTf(m,κ)，即所得函数内积为小波变换系数；ψ(t)∈L2(R)(平方可积空间)，称为母小波。

1.2 离散序列的多尺度分析

为了计算机实现处理多尺度分析，离散化必不可少，其方法是通过采用快速算法对分解系数进行处理。对于能量有限的物理信号f(t)，均可使用有限精度的分解法，如式(2)所示

(2)

式中：cj,k表示尺度系数；φj,k(t)表示尺度空间；dm.k表示小波系数；ψm,k(t)表示小波空间。

其中：

(3)

式中：h、g分别表示尺度空间和小波空间分解所对应的低通、高通滤波器。

将式(3)的递推一直进行下去，就会得到系数的“逐级分解”，此即为Mallat塔式分解算法，如式(4)所示。其分解算法如图1所示。从cj-1,k分解可得到cj,k和dj,k；反之，从cj,k和dj,k亦可重构得出cj-1,k，这种重构方案即称为Mallat重构算法。

(4)

图1 Mallat分解示意图Fig.1 Diagram of Mallat decomposition

实际应用的初始系数c0,k，在满足香农采样定理的前提下，直接将连续信号f(t)进行数字采样时得到的f[n]序列作为c0,k的近似表示。

本文对每个小波系数进行单支重构，得到原信号在该系数对应的尺度下的信号分量，其长度与原信号一致。

2 奇异值分解

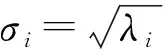
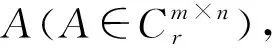
(5)

式(5)即为SVD的定义式，即表明矩阵A可以被分解为三个矩阵的乘积，其中S=diag(σ1,σ2,…,σr)表示奇异值(SV)向量，其中σ1≥σ2≥…≥σr>0，r=rank(A)。

3 基于小波变换与SVD的水电机组振动信号特征提取验证分析

水电机组采集的振动信号通常为一维时间序列函数，根据SVD的定义可知，处理分析对象为矩阵，对水电机组振动信号进行小波变换后得到单支小波重构系数，该重构系数用于构造SVD的输入矩阵，取SVD处理所得SV为信号特征参数。运用分类算法定量分析评价该方法特征提取效果。

3.1 信号获取

现有福建水口水电站一台机组发生了掉转轮室里衬的故障，转速为107.1 r/min，采样频率fs=458 Hz。采集得到水口电站该机组正常、故障预警与故障三种状态的轴向振动信号，波形图如图2所示。

为更准确地获得此信号的特征，对采集的水电机组振动信号，进行去噪处理，得到波形如图3所示。

3.2 特征提取

对已经进行去噪处理后的水电机组采集的振动信号进行小波分解。小波基函数选用DB8，分解的层数选用4层，利用MATLAB的小波函数wavedec进行分解，可以得到一系列小波系数，利用补零扩展模式的wrcoef函数处理各个一维的小波系数，分别对相应的小波系数进行重构，各系数进行小波重构所得波形如图4所示。

将所得的5组小波系数重构后所得序列，用于构造SVD的输入矩阵A，由于采样点为4 096个点一组，此时A∈C4 096×5，结合式(5)可得，存在酉矩阵U(U∈C4 096×4 096)以及酉矩阵V(V∈C5×5)，使得下式成立：

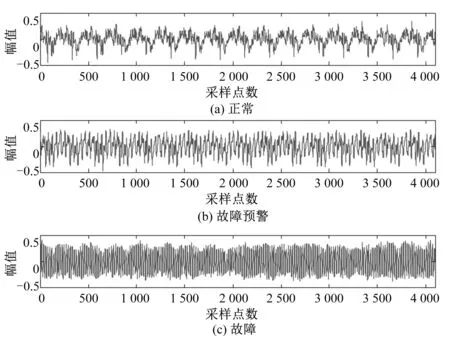
图2 原始振动信号波形图Fig.2 Original vibration signal waveform

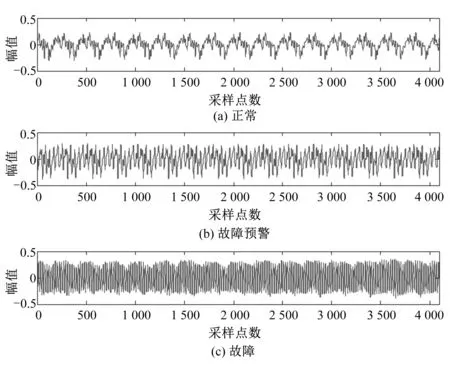
图3 去噪后的振动信号波形图Fig.3 Denoised vibration signal waveform

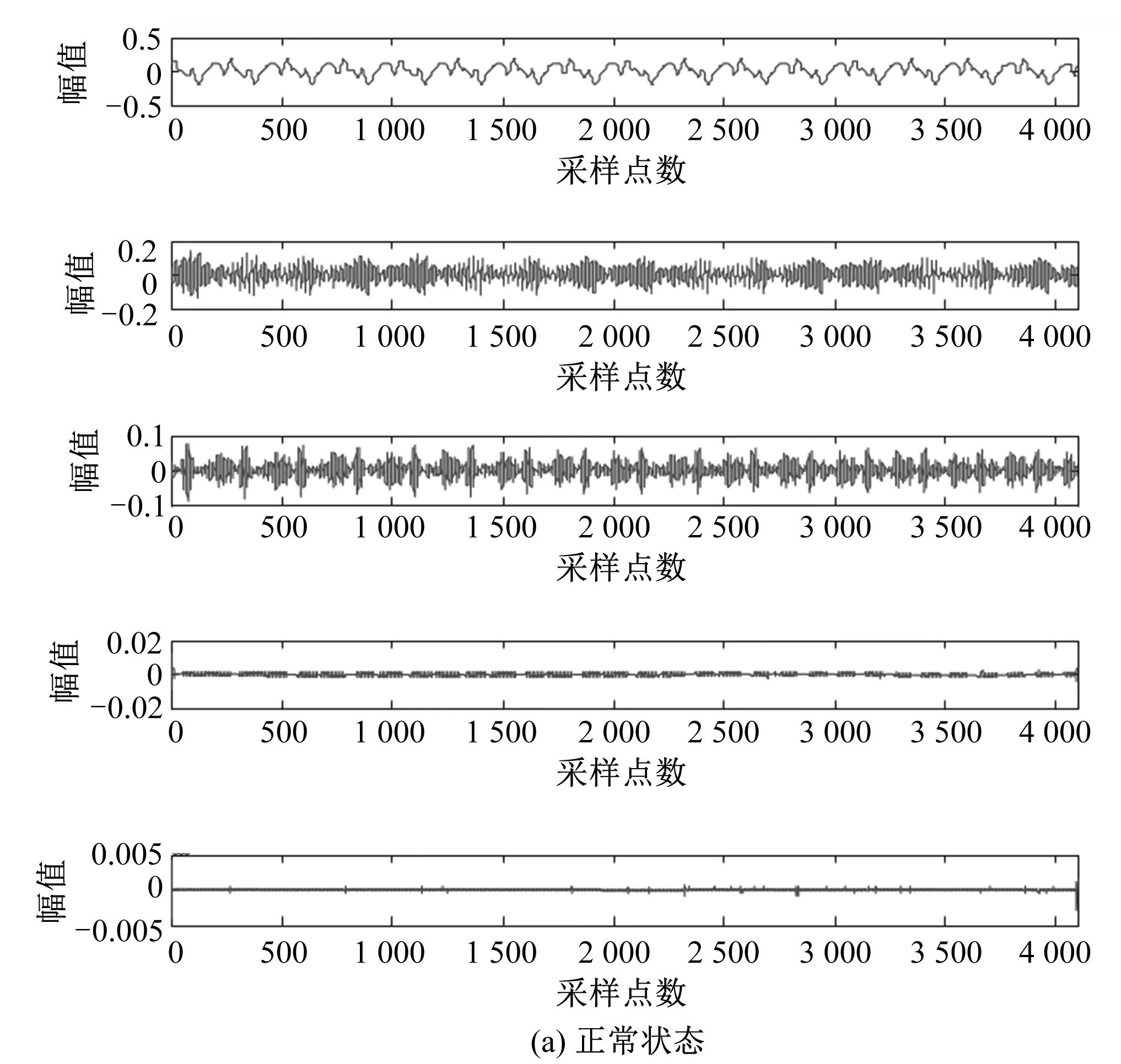
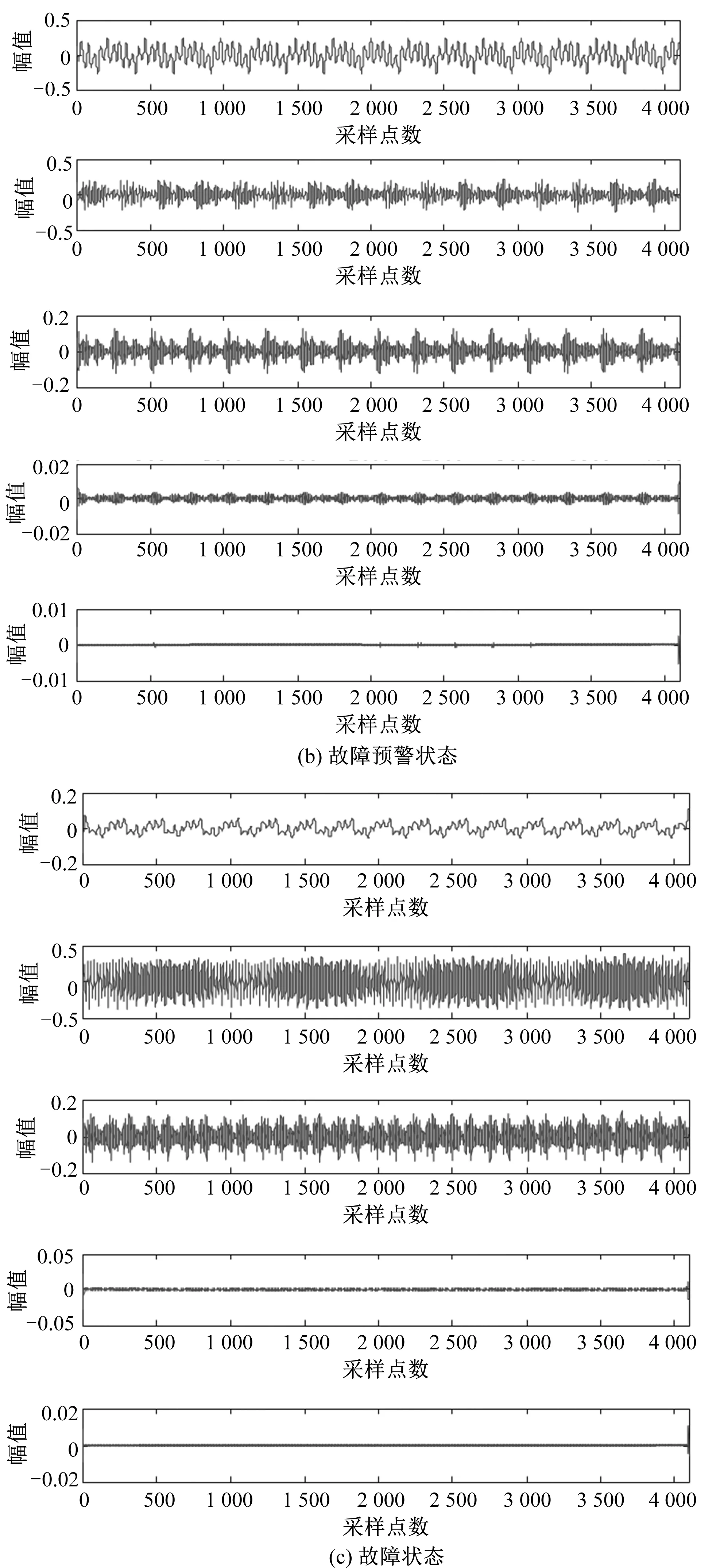
图4 不同状态下振动信号的小波系数重构波形图Fig.4 Wavelet coefficient reconstruction waveform of vibration signal under different states

(6)

式中：S=diag(σ1,σ2,…,σr)，同时有σ1≥σ2≥…≥σr>0，其中r=rank(A)=5。由于输入的矩阵为分解所得的σ1,σ2,…,σ5即为包含信号分量特征的SV，即(σ1,σ2,…,σ5)为表征信号特征的奇异值SV向量，即可用这五个SV作为水电机组振动信号的特征向量。

故障发生前后振动信号，经小波变换后进行SVD处理，提取的5个SV如表1所示。

从表1中SV数据不难看出，各个状态的水电机组振动数据经小波变换后，其重构系数用于SVD处理，所得SV数值具有一定数据特征，该SV特征数据实质反映了最大频率的能量特征，可以用于区分水电机组的状态。

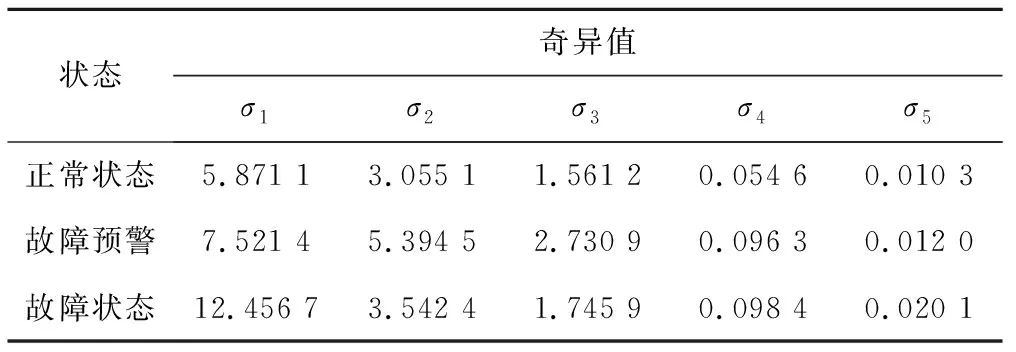
表1 不同运行状态振动信号经小波变换后提取的SVTab.1 SV of vibration signals extracted by wavelet transform under different operating states

3.3 验证分析

为了更加清晰直观地分析基于小波变换与SVD的特征提取效果，将机组不同运行状态下所得SV特征参数分别利用概率神经网络(Probabilistic neural network, PNN)进行分析。PNN的基本原理是通过应用贝叶斯决策规则，从多维空间分离出决策空间，使得误分类具有最小的期望风险。PNN是基于数学统计原理的前馈型人工神经网络，其激活函数是帕尔森窗函数。在模式分类中，由于结合了径向基神经网络和经典概率密度估计理论，PNN相比传统一些前馈神经网络优势明显。PNN结构框架如图5所示。

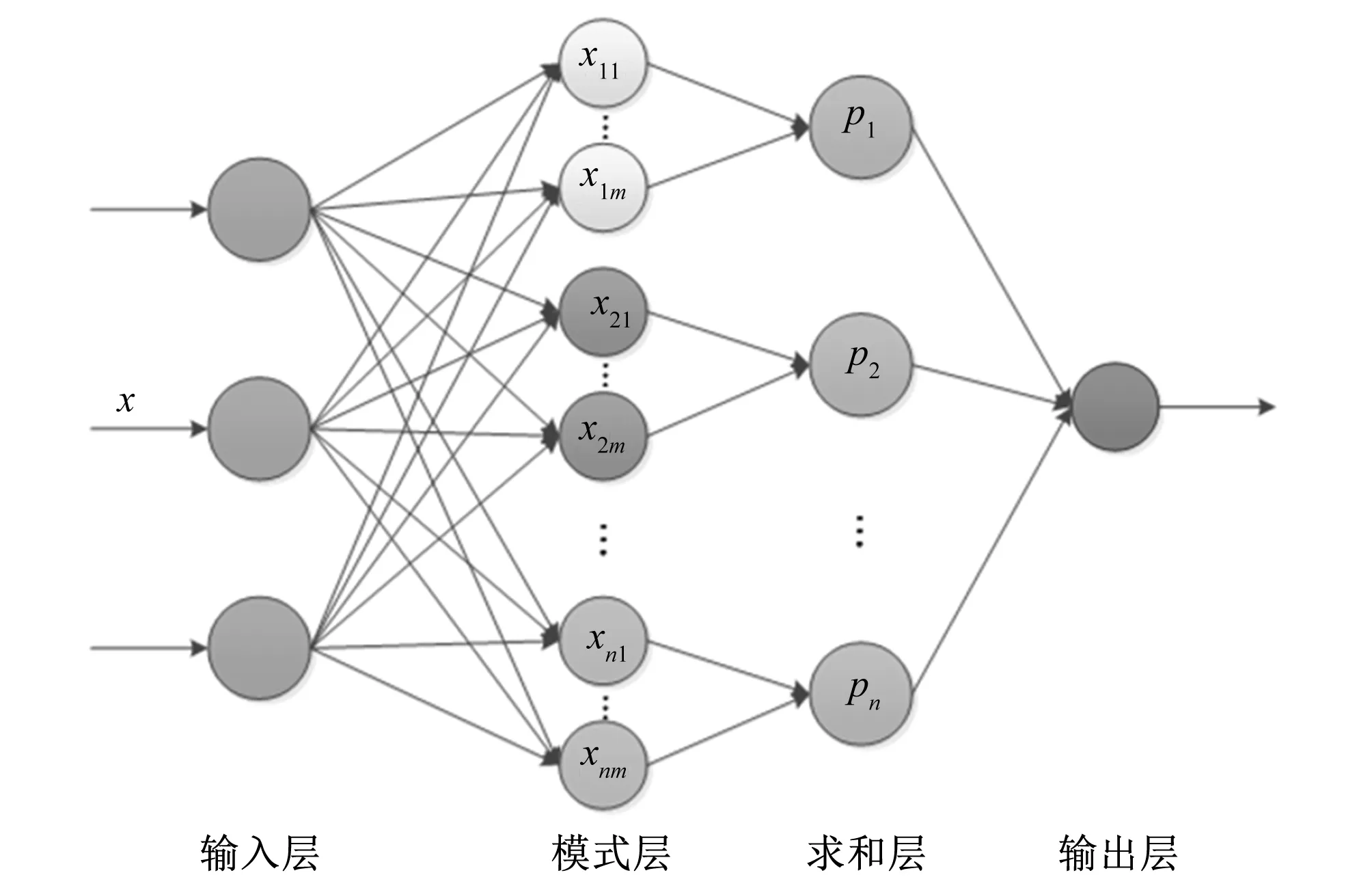
图5 PNN结构Fig.5 PNN structure

该网络由四层组成。第一层是输入层，表示输入向量X，本层的神经元数量等于X中变量数。模式层与输入层相连，每个神经元对应训练集中的一个样本。本层神经元的权值等价于不同的训练模式。计算输入层样本和训练样本之间的欧氏距离，并通过激活函数，得出输入样本与训练样本的相似程度(以[0,1]之间的小数形式表示)。求和层作用在于利用模式层每个神经元的输出计算每种模式下的综合概率。输出层将属于最大概率的模式作为最终结果输出。

随机取其中60组特征样本进行创建PNN，其中PNN的最优平滑系数取为0.03[8]，对剩余60组信号的特征信息进行有效分类，与真实情况进行比较，结果如图6所示。

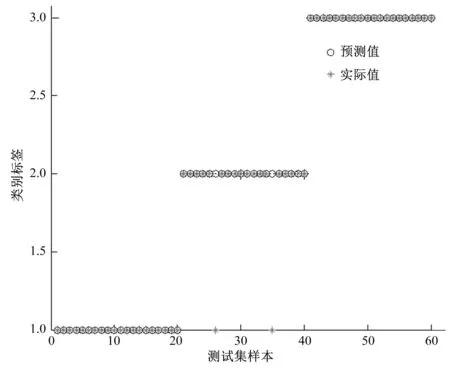
图6 小波-SVD的PNN分类结果Fig.6 PNN classification results of wavelet-SVD

从图6中可以直观看出，小波-SVD的PNN识别率总计为96.67%，分类效果较好。基于此表明基于小波变换与SVD相结合的特征提取方法对水电机组不同的状态区分较敏感，识别率较高。

4 结 语

合理的特征提取环节是对水电机组进行有效故障诊断的前提与关键，本文使用福建水口水电站的实际机组振动信号数据进行分析，提出基于小波变换与SVD的SV特征提取方法。对已进行去噪处理的信号，使用小波变换对信号进行分解，得到小波单支重构系数，对各支重构系数构造SVD输入矩阵，进行SVD处理变换得到SV。为验证SV特征参数效果，使用PNN法对提取的特征进行识别，结果表明基于小波变换与SVD的SV特征提取法便捷准确，对水电机组的状态故障区分敏感，可以为水电机组的故障诊断提供有效的依据。

□