基于SWAT模型和SUFI-2算法的黄柏河东支流域径流模拟研究

万 浩，董晓华，彭 涛，刘 冀，喻 丹，薄会娟，陈 亮

(1.三峡大学水利与环境学院，湖北 宜昌 443002；2.水资源安全保障湖北省协同创新中心，武汉 430072)

0 引 言

黄柏河流域位于湖北省宜昌市西北部，是宜昌市重要的水源地，也是著名的磷矿产区。近年来随着经济的不断发展和磷矿的大量开采，流域生态系统的结构和功能遭到严重损害，引发了一系列的生态与环境问题，例如流域水环境恶化、水土流失以及河道断流等现象，水资源保护形势日趋严峻[1,2]。水作为污染物传输和转化的基本载体，是维持生态平衡的物质基础，因此准确模拟径流的变化规律是流域水资源管理和规划的重要基础[3]。流域水文模型是研究水文循环过程的重要工具。现有的水文模型可以分为集总式水文模型和分布式水文模型，其中分布式水文模型能够准确模拟下垫面和降雨的空间差异性，被广泛用于流域水文过程模拟的相关研究中[4]。SWAT(Soil and Water Assessment Tool)模型是美国农业部(USDA)农业研究中心(ARS)于20世纪90年代开发并不断完善的一个流域尺度的分布式水文模型。SWAT模型具有较强的物理基础，能够模拟流域气候、土壤条件、土地利用以及管理措施变化下的水沙、营养物、杀虫剂等物质的运移[5]。在国内外，SWAT模型已得到了广泛应用[6,7]。

SWAT模型参数众多，很多参数难以直接获取，且同时需要考虑不同子流域参数的空间差异性，参数率定是一项繁杂的工作。此外模型是将复杂的水文现象和过程经概化后的近似的数学物理模型，其中存在着模型结构、模型输入和模型参数这三个方面的不确定性。因此，采用合理的参数率定方法对于提高模型模拟精度和模型的可靠性格外重要。序贯不确定拟合法(Sequential Uncertainty Fitting ver2，SUFI-2)作为近年来使用较多的不确定性分析方法，可以方便快捷地对SWAT模型进行参数率定，验证和不确定性分析，对于模拟精度和运算效率都有很大的提高。

以往对于黄柏河的研究，都主要集中在流域的水质评价以及污染成因分析，采用分布式水文模型来研究流域的径流过程的研究较少。本文构建黄柏河东支流域SWAT模型，进行流域的月径流模拟，同时运用SUFI-2算法进行模型的率定、验证和不确定性分析，以期为黄柏河流域的水资源高效管理规划提供科学依据。

1 数据与方法

1.1 研究区概况

黄柏河位于宜昌市西北部，是长江葛洲坝库区最大的一条支流，干流全长162 km。黄柏河在夷陵区两河口以上分为东西两支，东支发源于宜昌市夷陵区黑良山，东支干流长130 km，集雨面积1 165 km2，河道平均坡降0.6%。流域地势为北高南低，北部海拔1 300～1 900 m，中部海拔1 000～1 200 m，南部海拔200～800 m。黄柏河流域属于亚热带季风性湿润气候，四季分明，雨量丰沛，多年平均气温16.9 ℃，多年平均降水量1 138 mm，且降水分布具有明显的季节性，降水主要集中在6-9月，暴雨、短时强降水等灾害性天气多发。

黄柏河流域水能资源丰富，多年平均径流量约8.95 亿m3，由上游到下游建有玄庙观、天福庙、西北口、尚家河水库，流域供水覆盖了宜昌市50%的人口，是宜昌市的重要水源地。本研究选择黄柏河东支尚家河水库以上流域作为研究区(图 1)，研究区面积为932.26 km2。

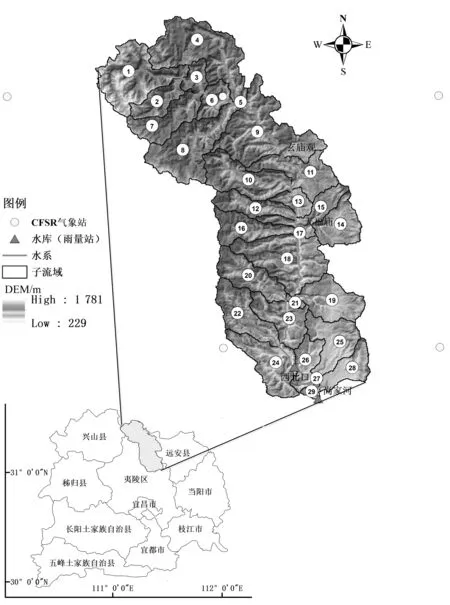
图1 研究区概况Fig.1 Overview of the study area

1.2 数据来源及处理

SWAT模型的输入数据主要包括：数字高程DEM、土地利用数据、土壤数据以及气象数据。其中DEM数据、土地利用和土壤栅格数据需要采用相同的投影坐标系统。根据研究区的地理位置，本文采用WGS-1984地理坐标系统和6°分带的UTM(通用横轴墨卡托)投影坐标，带号为49N，中央经线为111°E。

本研究所用的DEM高程数据来源于地理空间数据云(http://www.gscloud.cn/)提供的SRTM数据，分辨率为90M，研究区的DEM图如图 1所示。土地利用数据是基于Landsat8遥感影像，数据来源于地理空间数据云(http://www.gscloud.cn/)，使用ENVI5.1软件采用K-Means非监督分类[8]的方法进行遥感解译得到，如图 2(a)所示。根据SWAT模型数据库的要求，进行土地利用编码，各土地利用类型与SWAT模型编码的对应关系如表 1所示。本研究的土壤数据来源于联合国粮农组织(Food and Agriculture Organization-FAO)和维也纳国际应用系统研究所(International Institute for Applied Systems Analysis-IIASA)构建的世界协调土壤数据库HWSD(Harmonized World Soil Database)。本文采用魏怀斌等[9]提出的方法来构建研究区的土壤数据库。土壤类型的采用FAO-90土壤分类系统，研究区共有5种土壤类型，图 2(b)显示的是研究区的土壤空间分布情况，各土壤类型的面积及对应编码见表1。SWAT需要输入日尺度的气温(日平均、最高和最低)、太阳辐射，风速、相对湿度、降水、天气发生器等数据来驱动模型。本研究采用美国国家气象预报中心(National Centers for Atmospheric Prediction-NCEP)的全球气候再分析系统(Climate Forecast System Reanalysis-CFSR)提供的全球高精度气候变量数据来构建研究区的天气发生器。

图2 研究区土地利用图及土壤类型图Fig.2 Land use map categories and soil map of the study area

序号土地利用类型SWAT编码面积/km2比例/%FAO90土壤名称面积/km2比例/%1荒地BARR1.010.10ATc人为土41.521.772耕地AGRL142.1715.25LVh1高活性淋溶土1163.8217.573水域WATR12.381.33LVh2高活性淋溶土2439.7347.174林地FRST758.9381.41LVh3高活性淋溶土3270.7229.035城镇URBN17.771.91ALh高活性强酸土16.474.46 合计 932.26100合计932.26100

降雨采用位于流域内4座水库大坝处(图 1)雨量站的2008-2016年实测日降雨数据。因缺乏实测数据，其他气象数据则采用构建的天气发生器模拟。各水库的日平均出入库流量来源于黄柏河流域管理局提供的逐日观测数据。

1.3 研究方法

1.3.1 SWAT模型

SWAT是分布式的物理-概念水文模型，采用分布式计算。SWAT模型的原理参见SWAT官方网站的相关技术文(http://swat.tamu.edu /documentation)，此处不再赘述。

为了准确模拟研究区的2008-2016年的月径流过程，本文基于研究区的DEM、土地利用、土壤和日尺度的气象数据建立研究区的SWAT模型。根据DEM数据，并结合流域实际情况和模型的计算效率，设定集水面积划分阈值为2 000 hm2，并手动将4个水库出口添加为子流域出口，最终将研究区域划分为29个子流域，如图1所示。土地利用类型、土壤类型的划分阈值为5%，坡度类型划分阈值为10%，最终生成315个水文响应单元。SWAT模型的地表径流模拟采用SCS曲线法，河道汇流演算采用变动存储系数法，潜在蒸散发采用Penman-Monteith方法。

1.3.2 SWAT-CUP和SUFI-2算法

SWAT-CUP(SWAT Calibration and Uncertainty Programs)是Abbaspour等开发的一款可实现对SWAT模型进行参数敏感性分析、率定、验证和不确定性分析的计算机程序[10]。该程序包含了GLUE、ParaSol、SUFI2、MCMC和PSO五种优化算法，其中SUFI-2算法因为运行效率高，模拟效果好等优点，应用较广泛[11]。本文采用SUFI-2算法对所构建的SWAT模型进行参数敏感性分析、率定、验证和不确定性分析。

SUFI-2算法了考虑了水文模型的输入数据、模型结构和模型参数的不确定性，并用最后率定的参数分布范围来反映这些不确定性[12]。算法采用P-factor和R-factor两个指标来表征不确定性，P-factor表示在95PPU区间内包含观测数据的百分比，即95%置信区间包含的观测数据量。R-factor等于95PPU带的平均宽度除以观测值的标准偏差，反映95%置信区间内观测值的密集程度[13]。本研究选取2.5%～97.5%的区间作为SUFI-2算法的95%的置信区间(95PPU)，两个不确定性指标(P-factor、R-factor)计算方法参见文献[13]。理论上，P-factor的范围是0～1，R-factor的范围是0～∞。理想的情况是用最小的95PPU带去包含大部分观测数据(即P-factor等于1，R-factor接近于零)，但是通常一个较大的P-factor也对应着较大的R-factor[14]。因此，在率定的过程中，要综合权衡两个指标，使P-factor和R-factor均达到可接受的范围。

SUFI-2算法中提供了两种参数敏感性分析方法，One-At-a-Time(OAT)和全局敏感性(global sensitivity)方法。本研究采用全局敏感性分析对参数进行敏感性分析，敏感性计算公式见文献[13]。在分析中，采用t-Stat和p-Values来表示参数的敏感性。其中，t-Stat 表示参数的敏感性，p-Values表示敏感性的显著性。即t-Stat的绝对值越大和p-Values值越小，表示参数越敏感[15]。

2 结果与分析

2.1 敏感性分析结果

根据模型运算原理及各参数意义，参考Abbaspour等[16]的参数选择和总结，结合其他研究者的成果，选取与径流相关的19个参数进行全局敏感性分析。参数的原始范围是根据经验和参数的物理意义确定的，见表2。程序运行500次，得出敏感性分析结果见表2。

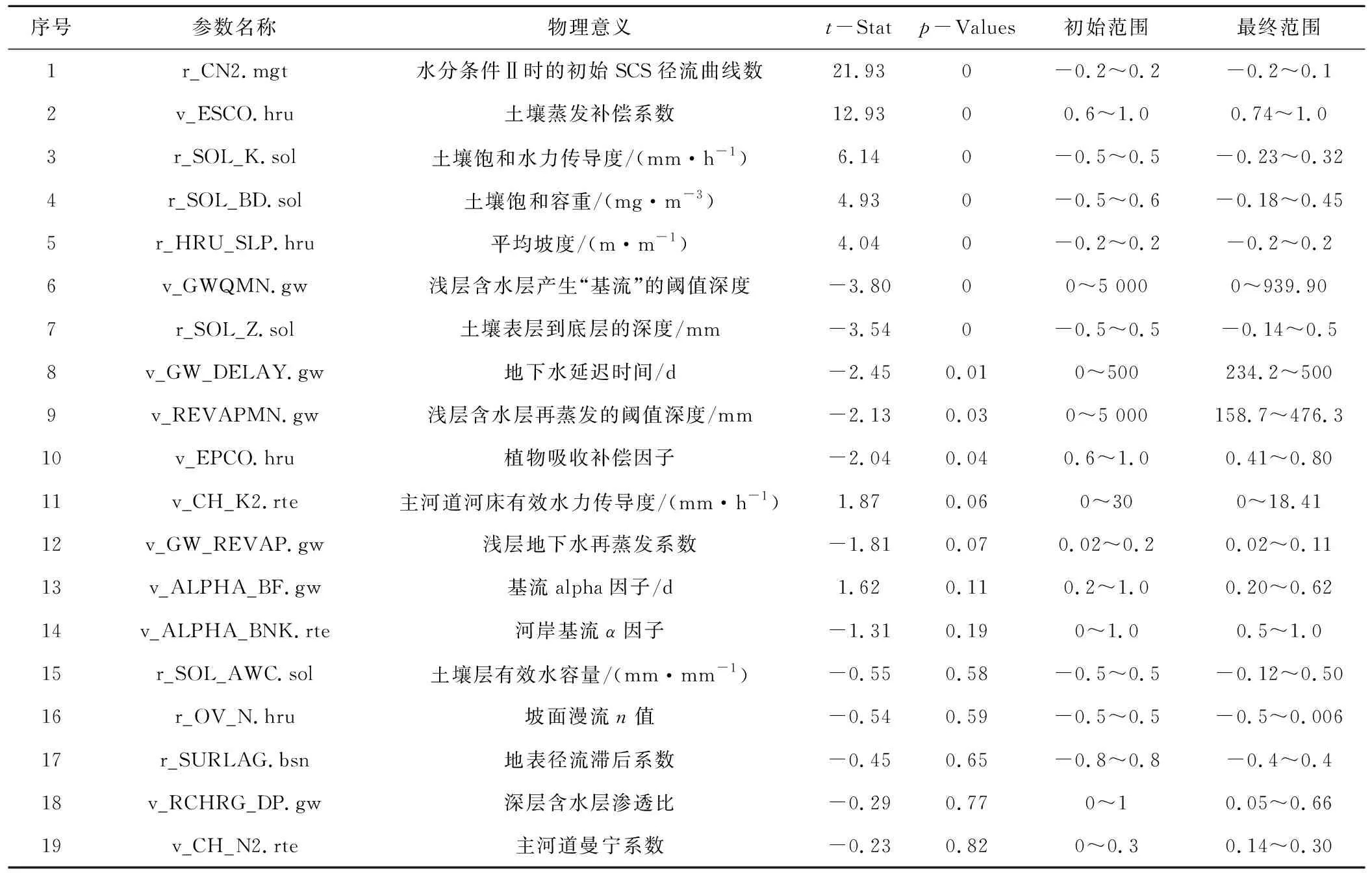
表2 参数敏感性分析及率定结果Tab.2 Sensitivity analysis and calibrated values for model parameters

注：v_是指绝对变化，直接替代原参数值；r_是相对变化，用原始值乘以(1十变化值)。

从表2中可以看出对黄柏河东支流域月径流模拟结果最为敏感的参数依次为：水分条件II时的初始SCS径流曲线数(CN2.mgt)、土壤蒸发补偿系数(ESCO.hru)、土壤饱和水力传导度(SOL_K.sol)等。CN2是采用SCS曲线法计算地表产流的关键参数，其值直接影响着径流量的大小。与其他湿润地区的研究[17,18]相比，相同的敏感性参数有CN2、ESCO、SOL-K、GWQMN，说明这些参数对于湿润地区的径流模拟有重要影响。

2.2 参数率定和验证结果

选取2008年为模型的预热期，以降低模型在运行初期初始条件的影响。2009-2013年为模型率定期，2014-2016年为验证期，进行黄柏河东支流域的月径流模拟。选取国内外文献[19,20]中普遍使用的Nash-Sutcliffe Efficiency纳什系数(NSE)、均方根误差与标准差比值(ratio of root mean square error to standard deviation，RSR)和百分比偏差(Percent Bias，PBLAS)来综合评价模型的模拟精度，各评价指标的计算方法见文献[20]。一般认为NSE>0.5，RSR<0.7，|PBLAS|<25%时，模型模拟结果是可以接受的。

SUFI-2算法是通过不断迭代来获得最佳参数范围，每次迭代都会计算目标函数和参数之间的相关性，然后为下一次迭代提出新的参数范围。需要注意的是，在迭代过程中，一些建议的参数范围超出了参数的物理意义，需要对这些参数进行手动调整，使它们不超过最大/最小绝对值的范围。本研究共进行了3次迭代，每次迭代运行500次，得出了最终的结果，参数率定结果见表2。

月径流率定和验证结果见图3和表3。由图3可以看出，玄庙观、天福庙、西北口和尚家河站的SWAT模型模拟的月径流过程线与实测月径流过程线较为吻合，对于洪峰均有响应。各站的均方根误差与标准差比值RSR均小于0.7，在误差范围内。纳什效率系数NSE除玄庙观站为0.64外，其余各站均在0.75以上，西北口和尚家河站都达到了0.9以上，模拟精度较高。在验证期，各站点的纳什效率系数NSE均在0.85以上，相对于率定期均有所提高，这可能是由于验证期相对于率定期时间较短，参数拟合相对较容易。同时发现，在率定期和验证期下游站点的模拟精度都高于上游站点，上游站点所控制的流域面积较小，径流受人类活动的影响较大。最上游的玄庙观站在率定期和验证期纳什效率系数NSE均最小，分析原因可能是由于玄庙观站受流域内磷矿开采影响较大，流域水循环模式改变显著，一部分地表径流进入磷矿开采所形成的矿坑，这增加了模型模拟的难度。另外，根据调查玄庙观流域内建有小水电站，模型未能考虑小水电调洪等人类活动的影响，对于模型模拟精度也有影响。

表3 黄柏河东支流域月径流模拟结果统计Tab.3 Evaluation of monthly runoff simulation results

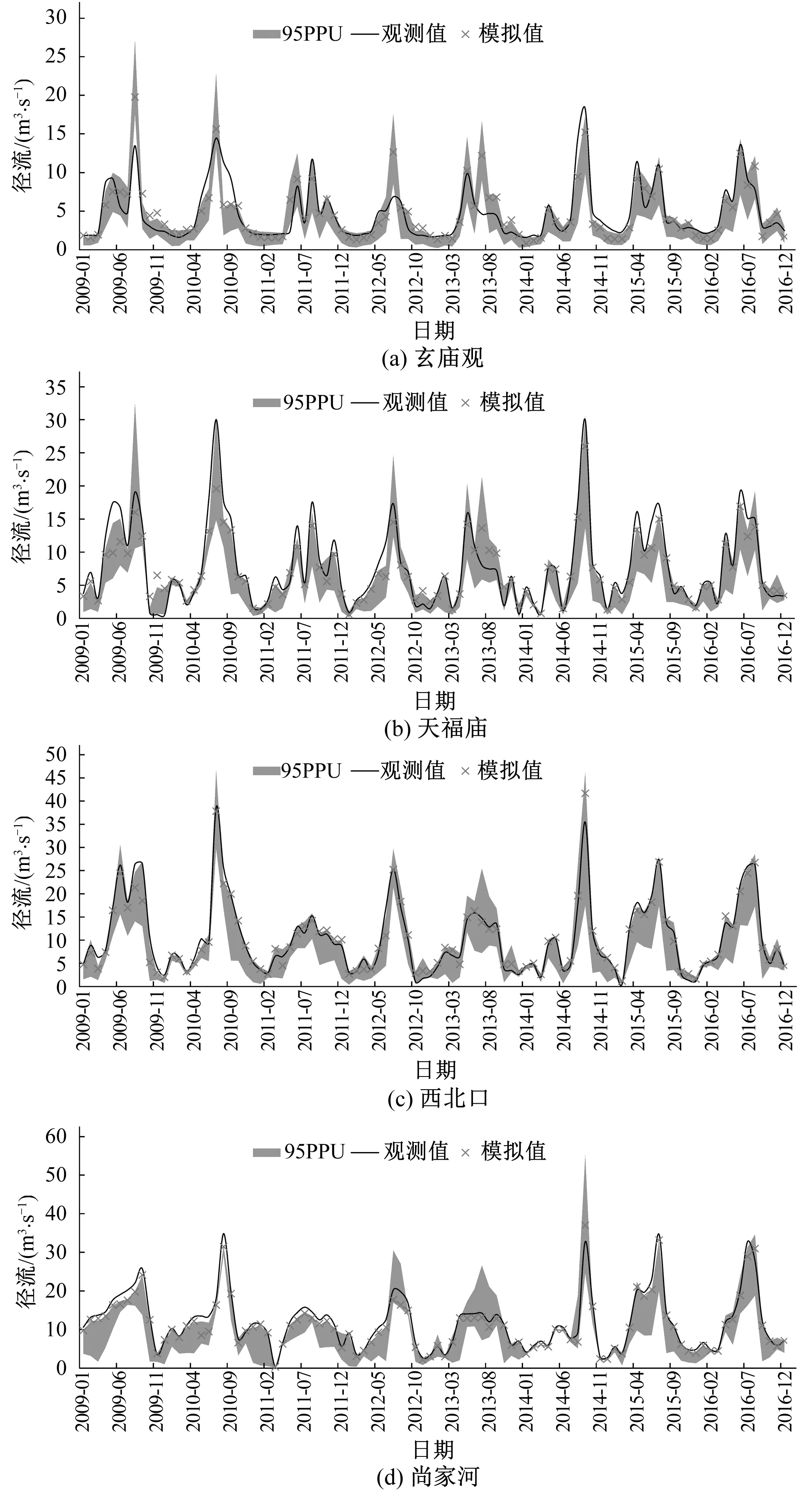
图3 黄柏河流域各站月径流观测值和模拟值对比及95PPUFig.3 Observed,simulated and 95PPU of monthly runoff in calibration period

对于百分比偏差PBIAS而言，大部分站点在率定期和验证期的PBIAS值均大于0且小于25%，说明模型在率定期和验证期月径流模拟结果较观测值偏低。整体来看，3个评价指标均在误差范围内，SWAT模型能够较好地模拟研究区的月径流过程，在流域的月径流模拟中具有较好的适应性。

2.3 不确定性分析结果

不确定性结果见表3。在验证期和率定期各站点的P-factor均大于0.65，R-factor均小于1、表明大多数观测值落在95PPU区间内，所构建的SWAT模型径流模拟的不确定性较小。

除玄庙观站外，验证期和率定期相比，各站点的不确定性均有所降低，观测值落在95PPU区间内的个数增多。在率定期，天福庙的P-factor最小，径流模拟的不确定性最大，但是天福庙站的纳什效率系数NSE并不是最小的，这表明模型的不确定性结果并不完全和模型模拟精度相一致。较大的参数范围能够反映出参数对模拟结果的影响，但由此产生较宽的不确定性区间，降低了模拟的置信水平。在参数率定的过程中，综合考虑了模型的模拟精度和模型率定的不确定性，来提高模型模拟的可靠性。

3 讨 论

由表3可知，玄庙观、天福庙两个水库坝址处的径流模拟结果比另外两个水库坝址处的模拟结果要差。原因可能是因为人类大量的采矿活动改变了流域下垫面条件。为了进一步分析这两个水库坝址处径流模拟结果较差的原因，图4给出了流域降雨的空间分布[图 4(a)]、实测径流深分布[图 4(b)]以及磷矿位置。

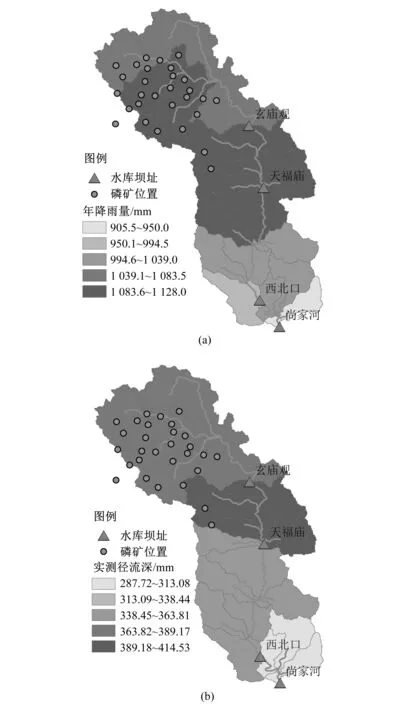
图4 降雨径流空间分布Fig.4 The spatial distribution of annual rainfall, runoff depth in the study area

由图 4(a)可以看出，磷矿均位于天福庙水库以上的区域。流域的年降雨量从上游到下游呈递减趋势，河流右岸地区高于左岸地区，年降雨量中游最高，下游流域出口地区降雨量最小。比较图 4(a)和图 4(b)可以发现，天福庙以上区域的降雨量较大，但是并没有产生相应较大的径流深。特别是在上游磷矿密集分布区域，降雨量大而径流深却小。由于玄庙观、天福庙以上区域磷矿分布密集，我们认为造成径流深减少的原因是由于磷矿开采活动引起的。磷矿开采过程中形成的地下裂隙、矿洞和矿坑，下渗的降水通过这些地下通道大量流失，从而减少了地表径流。这与文献[21]的研究结果相同，即磷矿开采减少了径流量。

磷矿开采活动改变了流域下垫面条件，使地表径流通过矿洞、裂隙等通道进入地下。由于SWAT模型对地下水过程的模拟比较简单，仅仅分为浅层和深层含水层，因此使得玄庙观、天福庙两个水库坝址处的径流模拟精度远低于另外两个水库坝址处的径流模拟精度。如果需要提高天福庙以上区域的径流模拟精度，需要改进SWAT模型中的地下水模拟模块，或将SWAT模型与VISUAL MODFLOW等地下水模型耦合，使其能够模拟磷矿开采对径流的影响，提高流域径流模拟的精度。

4 结 语

本文在黄柏河东支流域构建了SWAT模型，运用SWAT-CUP软件中的SUFI-2算法进行了模型参数的敏感性分析、率定和不确定性分析，对研究区的月径流进行了模拟。主要结论如下。

(1)参数敏感性分析结果表明，在所选取的19个与径流相关的参数中，CN2、ESCO、SOL_K最为敏感，对研究区的月径流模拟结果影响最为显著。

(2)应用SWAT模型进行黄柏河流域的月径流模拟可以取得较满意的结果，多数站点在率定期和验证期的NSE均大于0.75，流量过程线拟合程度较好，表明SWAT模型在研究区具有较好的适用性。

(3)采用SUFI-2方法的不确定性分析表明，各个站点的不确定性都较小，大多数观测值落在95PPU区间内，验证期的不确定性小于率定期。其中，天福庙站的径流模拟精度虽然较高，但是其模拟结果的不确定性最大，说明模拟精度和不确定性结果并不一致，需要在模拟精度和模拟结果的不确定性之间取得平衡。

(4)模拟结果表明，流域上游径流模拟精度低于下游，原因是上游区域大量存在磷矿开采活动，这一人类活动改变了流域的下垫面条件，增加了SWAT模型的模拟难度，预计通过改进SWAT模型的地下径流模块可以提高径流模拟精度。

□