面向区域覆盖的多传感器优化布站*

俞宙，单甘霖，段修生,2

(1.陆军工程大学 石家庄校区，河北 石家庄 050003；2.石家庄铁道大学，河北 石家庄 050003)

0 引言

随着电磁干扰、反辐射导弹、超低空突防、隐身武器的快速发展，战术侦察系统面临着巨大的挑战和威胁[1]。战术侦察系统目前配置了不同体制、不同功能、不同频段的雷达、红外、激光和侦察车等传感器，对目标区域进行协同探测。传感器位置不同得到的侦察效果也不同，为了获得最佳探测效果、提升系统生存能力，必须根据传感器数量确定优化布站方式。

文献[2]提出的雷达配置算法，综合考虑了雷达覆盖图，RCS(radar cross section)，带宽等因素。文献[3]考虑雷达节点受距离限制，采用演化优化算法进行网络拓扑设计。文献[4]将目标发现概率和雷达功能仿真相结合，构建了雷达探测概率仿真模型。文献[5]考虑了地球曲率对目标定位精度的影响，讨论了GDOP(geometrical dilution of precision)对传感器几何布站的影响。文献[6]解决了无线传感器网络中覆盖和节能之间的权衡问题。文献[7]讨论了传感器几何形状对定位精度的影响。文献[8]解决了最小距离传感器的线段覆盖问题。在文献[9]的基础上，文献[10]提出了一种基于改进遗传算法的雷达网优化布站方法，给出了求解过程和步骤。文献[11]提出了一种基于改进粒子群算法的雷达布站优化算法,改善了算法搜索性能不强的缺陷。文献[12]将区域划分为中心和边缘区域，确保无线传感器的连通性和覆盖范围。文献[13]建立了雷达圈、线、扇形配置模型，但未进行有效求解。文献[14]建立了一种简要阵地约束条件下探测覆盖系数的雷达组网模型。文献[15]考虑地形因素，但只考虑了可用凸多边形建模的地形。

针对现有传感器布站模型不能解决复杂战场地理和战术条件限制下的传感器布站问题，本文根据具体侦察任务要求，在充分考虑各种限制条件的基础上，构建了战场多传感器优化布站的结构和模型，解决了复杂战场地理条件下传感器布站受限问题。在此基础上，提出了一种基于遗传粒子群算法的多传感器优化布站方法，增强了粒子群算法的全局寻优能力。并通过仿真验证了构建的战场多传感器优化布站模型的可行性，以及基于GA-PSO的多传感器优化布站方法的有效性。

1 优化布站任务描述

1.1 明确任务

某次侦察任务中，上级命令对某城市及周边区域进行协同探测，并对中心市区进行重点探测。根据重要程度不同，把上级要求覆盖的区域作为责任区域，把中心市区作为核心区域。

责任区域是指该区域至少能被一部传感器所覆盖，表示为Ar。核心区域相对重要，要求该区域至少能被2部以上的传感器所探测，即传感器重叠系数K≥K0(K0>1)，表示为Ac。因此，两者之间的关系为：Ac⊂Ar。

1.2 布站要求

基于以上任务需求，为了合理利用传感器资源，提出以下布站要求[16]：

(1) 责任区内实现最大探测范围；

(2) 远、中、近距离探测一体化；

(3) 机动、屏蔽与防护一体化；

(4) 频率与空间一体化。

此外，布站阵地的选择还应该考虑生存因素、战场地理和战术条件等因素。

2 战场多传感器优化布站模型

2.1 传感器探测

假设战术侦察系统中有N部传感器S={S1,S2,…,SN}，传感器Si的位置点坐标为(xi,yi,zi)，对于责任区内任意一个位于(xj,yj,zj)的目标点Tj，传感器和目标之间的距离为

(1)

单传感器的探测概率Pi近似为

(2)

式中:k为参数,d为传感器与目标的距离，则探测概率只与传感器与目标之间的距离有关。

因此，多传感器Si对目标Tj的联合探测概率为

(3)

通常，传感器的探测范围大小与概率有关。一般要求责任区域内联合探测概率不低于某门限值P0，即Pall≥P0。即当确定P0以后，传感器的探测范围随之确定。

2.2 战场地理约束

实际应用中，传感器不能任意布站，其受到地理环境的约束(如湖泊、高山沼泽等)，同时应尽量避免具有强电磁干扰的设施(如机场、雷达站等)。此外，考虑到实际地理环境，布站责任区域往往形状极不规则，难以精确描述。为此，提出了一种网格化的地理环境模型。主要步骤如下：

(1) 责任区域网格划分

明确布站责任区范围以后，用平行线对责任区进行等间隔的网格划分，建立布站网格，每一个网格区域都是一个备选的传感器布站位置点。

(2) 建立布站约束矩阵

把责任区看成一个矩形，把其中的每一个布站位置点看成矩阵中的一个元素，建立布站约束矩阵BM×N。假设每一个布站点只能放一部传感器，BM×N中的元素bij(1≤i≤M，1≤j≤N)就代表责任区内的每一个布站点，则矩阵为

(4)

式中：布站约束矩阵bij描述了布站责任区内的布站位置点的地形状况，bij的取值bij={0,1,2},(1≤i≤M,1≤j≤N)根据责任区的地理情况来确定。并且有

(5)

式(5)表明，如果该点可以布站，则bij取值为1；如果该点不能布站，则bij取值为0；若该点是重点区域，且可以布站，则bij取值为2。

本次任务中，红方收到上级分发的责任区如图1所示，地图来自北方某城市。则责任区域布站网格划分如下，其中，红色标注的中心市区为核心区域。

根据对责任区域的网格划分，可以建立如下的布站约束矩阵BM×N。通常，网格划分越精细，对区域的描述就越准确，但同时会增大计算量。因此，布站网格的划分应根据具体任务及实际地形来确定。图2给出了M=N=20时的布站约束矩阵。

(3) 表达式描述

通过把布站约束矩阵的数值映射到布站网格上，将责任区域坐标化，用表达式来描述责任区域。

不能布站区域Aunable定义为由责任区域内所有不能布站的位置点组成的区域，表示为

Aunable=∪bij,bij=0.

(6)

可以布站区域Aable定义为责任区内所有可以布站位置点组成的区域，表示为

Aable=∪bij,bij=1∪bij=2.

(7)

则战场地理约束条件可以表示为

bij∈Aable≠Aunable

.

(8)

为了实现传感器之间的信息交互、协同探测、相互补盲的功能，传感器之间必须要有一定的距离限制，则相邻传感器之间的距离可以用式(9)来约束。

|ri-rj|≤d(Si,Sj)≤ri+rj,

(9)

式中：ri，rj为第i，j部传感器的探测范围。

因此，根据实际任务情况，构建上述的战场地理约束模型，可以简单地消除布站范围内不能布站区域对于传感器布站的影响，同时可以形成有效的数学约束条件，避免在制定优化布站方案时误选了不能布站的位置点。

2.3 战术条件限制

传感器布站通常考虑以下战术条件限制：

(1) 责任区域覆盖系数

责任区域覆盖系数α定义为实际获得的责任探测区域与责任区域的比值

(10)

式中：R为实际获得的最大责任探测区域；Ai为第i部传感器的探测范围。

(2) 核心区域覆盖系数

考虑到实际应用中，某些区域应该重点覆盖，因此，核心区域覆盖系数β定义为实际获得的核心探测区域与核心区域的比值

(11)

式中：C为实际获得的最大责任探测域。

(3) 频率干扰系数

为了避免因频率干扰影响系统的探测性能，频率有重叠的传感器布站时要尽量错开。频率干扰系数θ定义为相邻传感器之间同频干扰的程度

(12)

式中:fi表示第i部传感器的频率宽度，为了获得最佳抗干扰性能，通常θ的取值范围为[0,1]。

(4) 资源利用系数

通常2部传感器覆盖区域有重叠视为合理，3部及以上传感器覆盖区域有重叠视为浪费。资源利用系数η定义为3部以下传感器覆盖区域与核心区域的比值

(13)

为了合理利用资源，通常η的取值范围为[0,1]。

2.4 优化布站数学模型

为了在责任区域内获得最大覆盖范围，并对核心区域进行重点覆盖，同时避免传感器的同频干扰和资源浪费问题。综合考虑战场地理约束和战术条件限制，运用加权法建立如下的多传感器优化布站数学模型，通过优化求解，可以获得最佳的多传感器优化布站方案。

(14)

式中:F为最大探测区域覆盖能力；ωi为各指标的重要性程度，由指挥员综合考虑战场实际任务、目标重要程度、蓝方威胁程度等因素来决策。

若蓝方武器落后，进攻方式保守，红方可采取积极主动的策略，在责任区内获得尽可能大的覆盖区域，增大ω1的数值。若蓝方目标机动灵活，威胁较大，则应提高对核心区域的覆盖，增大ω2的数值。经专家论证本文取值ω1=0.3，ω2=0.5，ω3=0.1，ω4=0.1，能够满足作战需求。

3 多传感器优化布站算法

3.1 粒子群算法

粒子群算法(particle swarm optimization,PSO)将优化问题可行解初始化为一群随机粒子。粒子根据如下的公式来更新自己的位置和速度：

vi(t+1)=λvi(t)+c1r1(Pibest-Xi(t))+

c2r2(Pgbest-Xi(t)),

(15)

Xi(t+1)=Xi(t)+vi(t+1).

(16)

3.2 遗传粒子群算法

针对PSO计算函数极值时，容易出现早熟收敛、全局寻优能力较差等问题。我们将粒子群算法和遗传算法(genetic algorithm,GA)相结合，在PSO繁殖操作基础上增加GA的选择、交叉和变异操作，提出一种遗传粒子群算法(GA-PSO)对函数进行寻优计算。得出的GA-PSO增强了PSO的全局寻优能力，加快了进化速度，提高了收敛精度。下面我们详细讨论这2个操作。

3.2.1 选择、交叉操作

首先，依据某种策略(本文采用赌轮选择法)选出M(偶数)个个体，然后对选出的个体进行两两配对，以概率Pc执行如下交叉操作：

(17)

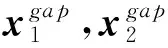
3.2.2 变异操作

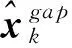
(18)

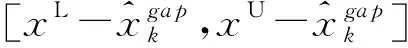
基于以上分析，可以得出GA-PSO算法的流程：

(1) 初始化种群中N个个体位置及速度，计算适应度值，找出个体极值和群体极值；

(2) 按式(15)和式(16)更新粒子的速度和位置，并计算它们的适应度值；

(3) 若满足结束条件则输出最优解，终止程序，否则继续执行(4)；

(4) 按适应度值随机选出M个个体执行交叉操作，得到M个新个体；

(5) 对所有个体执行变异操作，在M+N中选择适应度高的个N个体进入下一代，转向(2)。

4 实验结果与分析

4.1 GA-PSO算法性能测试

为了验证GA-PSO的有效性，通过大量的实验对PSO与GA-PSO算法进行寻优能力对比分析，本文选取2个经典的测试函数Rastrigrin和Griewank进行实验。实验中，粒子数目100，迭代次数200，重复实验100次，搜索空间[-50,50]，实验结果如图3，4和表1所示。

Rastrigrin

(19)

Griewank

(20)

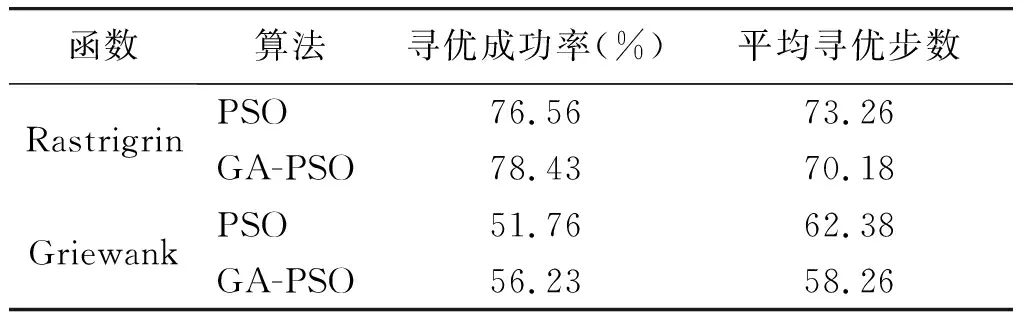
函数算法寻优成功率(%)平均寻优步数RastrigrinPSO76.5673.26GA-PSO78.4370.18GriewankPSO51.7662.38GA-PSO56.2358.26

4.2 多传感器优化布站

此次任务中，侦察区域的范围为100 km×100 km，核心区域范围为20 km×20 km。为通过对比分析，可以看出GA-PSO的收敛速度明显快于PSO，对于寻优有着加速作用，且寻优成功率高于PSO，全局寻优能力更强。

因此，基于GA-PSO的多传感器优化布站方法流程如下，流程图如图5所示。

(1) 明确作战任务，进行需求分析；

(2) 导入责任区域地图，进行区域划分；

(3) 建立战场地理约束模型；

(4) 考虑战术条件限制，建立战场多传感器优化布站模型；

(5) 采用GA-PSO算法求解；

(6) 获得优化布站方案；

(7) 若满足要求，终止程序进行(8)，否则转向(6)进行实时调整；

(8) 根据优化布站方案进行传感器布站。

4.2 多传感器优化布站

此次任务中，侦察区域的范围为100 km×100 km，核心区域范围为20 km×20 km。为了避免传感器数目过多造成资源浪费，采用4部传感器进行布站。在第Ⅰ种环境中，探测概率P0取为0.7，确定4部传感器的最大探测半径分别为25,30,30,30 km。第Ⅱ种环境中，当探测概率P0取为0.8时，确定4部传感器的最大探测半径分别为20,25,30,35 km。初始种群为200，权重λ取为1，最大迭代次数为200，交叉概率Pc为0.7，变异概率Pm为0.05，采用PSO和GA-PSO算法进行优化计算，运行结果如表2所示。

由表2绘制的GA-PSO布站情况如图6，7所示。由仿真实验效果图可以看出，在实际布站时，当给定责任区内有不可达的地域时，本文提出的基于GA-PSO优化布站方法较PSO有了明显的优化，在满足侦察任务要求基础上，成功地解决了制定布站方案时布站地形条件的约束问题，避免了传感器落入不能布站区域，确保布站方案能够顺利实施。

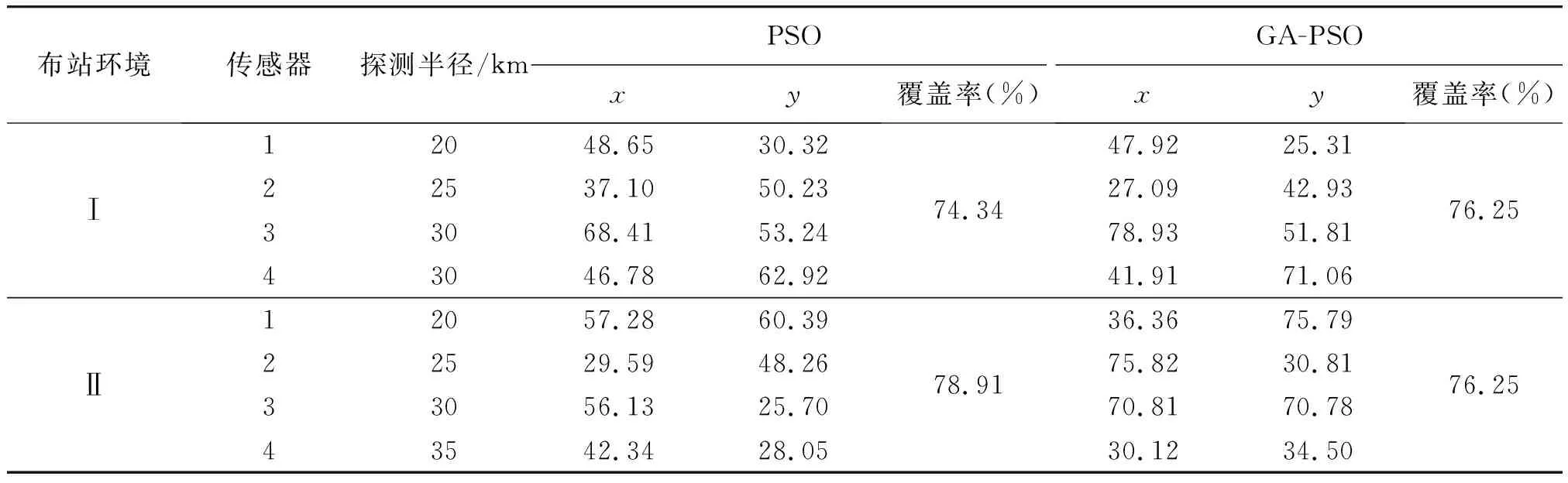
表2 GA-PSO求得的四部传感器坐标

5 结束语

本文根据具体侦察任务，描述了多传感器优化布站问题。在充分考虑各种限制条件的基础上，建立了多传感器优化布站模型。针对该模型，提出了一种基于遗传粒子群算法的多传感器优化布站方法，增强了粒子群算法的全局寻优能力，加快了进化速度，提高了收敛精度。通过仿真给出了传感器最优布站位置，验证了所提出的传感器优化布站模型的可行性，以及基于GA-PSO的传感器优化布站方法的有效性。