民用飞机某型前轮转弯偏离角度计算方法研究
周 佳
(上海飞机设计研究院,中国 上海 201807)
0 引言
本文某型飞机为基础, 研究一种民用飞机接通前轮转弯情况下直线滑行时出现偏离倾向时的角度计算方法, 通过对飞机前轮转弯进行数学建模分析, 计算得出飞机直线滑行时的偏离角度, 通过对前轮转弯系统预设参数的调整实现飞机纠偏, 提高了飞机的前轮转弯性能, 对飞机的生产试飞和航线运营具有较大的指导意义。
1 民用飞机某型前轮转弯系统介绍
飞机的前轮转弯系统是飞机地面操纵性的重要指标, 当飞机低速滑行时能够使飞机具有良好的地面机动能力; 当飞机高速滑行时能够保持航向和提供足够的液压阻尼, 防止起落架发生摆振, 并对航向进行纠正。
2 前轮转弯系统偏离角度计算研究
2.1 问题背景
某型飞机在生产试飞时,需要检查飞机15 节速度直线滑行时接通前轮转弯后飞机直线滑行保持能力。当飞机出现较大偏离倾向时通过Trimming 对前轮转弯进行调整配平,但是飞机出现偏离倾向时CMS 上无法显示一个确定的偏离角度,EICAS 也无相关的告警信息; 可是飞机实际已出现了明显的偏离倾向, 需要对飞机前轮转弯系统进行Trimming 调整配平。 具体配平多少一般按经验结合之前架次飞行数据确定, 没有具体的计算公式。
某型飞机前轮转弯系统可以通过飞机中央维护系统(CMS)进行机械电子调零(Rigging)和通过修改SCU的预设值对前轮转弯系统进行配平 (Trimming)。 前轮Trimming 可调节范围为±1°, 即可对±1°范围内的飞机偏离倾向进行调节配平。
2.2 三点式前轮转弯偏转模型
某型飞机采用前三点式起落架布局, 根据飞机偏转的现象进行以下三种数学建模分析。
a.简化点模型
将飞机整体简化为一个点, 飞机直线滑行由起始点开始到终止点结束, 连接起始点到终止点直线简化为飞机实际运行轨迹L, 飞机终止点距离垂直线位移H 为可实际人工测量的飞机水平偏离量,L、H 和垂直线构成一个三角模型, 通过数学计算可得出飞机偏离角度α,具体见图1。

图1 简化点模型
以上模型将飞机整体简化为一个点, 将起始点和终止点连线简化为飞机实际运行轨迹, 但此模型存在一定问题即默认飞机在初始状态时以一个确定的偏转角度滑行, 但整个滑行过程中默认飞机沿直线滑行至终止点。 经分析此简化模型与飞机实际滑行过程差别较大, 飞机滑行整个过程偏离一直存在并非仅在初始状态存在偏离。
采用此模型进行实例计算举例: 飞机滑行速度15节,跑道宽45 米;飞行机组记录飞机直线滑行时间15秒后飞机偏离跑道中轴线距离约占跑道1/8。 即L=115.65,H=5.625, 带入公式计算得出偏离角度α=2.8°;实际飞机调整0.5°后可保持直线滑行。 通过此模型计算得出偏离角度2.8°相对实际验证角度0.5°差距较大,且实际trimming 范围为±1°。 此模型不符合实际飞机前轮转弯偏离过程, 计算得出的偏离角度仅表示飞机由起始点到终止点时飞机最终的偏离角度,不能代表飞机动态实时偏离倾向角度, 因此以上数学建模不够严谨。
b.微积分模型
将飞机整体简化为一个点, 飞机直线滑行由起始点到终止点运行轨迹L 简化为n 段直线段, 每段飞机滑行轨迹为L1、L2、L3……对应每段偏离距离H1、H2、H3……采用微积分形式, 飞机实际运行轨迹整体近似为一个圆弧形,飞机终止点距离垂直线位移H 为可实际人工测量的飞机水平偏离量, 通过数学建模计算飞机偏离角度α,具体见图2。
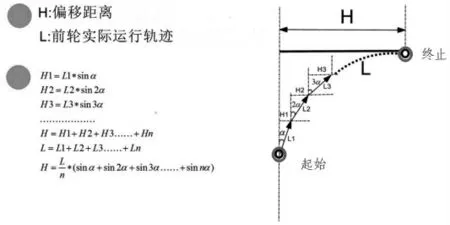
图2 微积分模型
采用此模型进行实例计算举例: 飞机滑行速度15节,跑道宽45 米;飞行机组记录飞机直线滑行时间15秒后飞机偏离跑道中轴线距离约占跑道1/8。 由与以上建模求解计算时, 当n 趋近于无穷时函数不收敛,角度α 无解,所以以上建模不成立。
c.三轮车模型
将飞机整体简化为一个三轮车模型, 如图4 中蓝色三角所示;飞机前轮和主轮距离为h,当飞机带偏离倾向滑行时, 飞机前轮由起始点运行到终止点, 运行轨迹L 为半径R 的圆弧,飞机起始点位置沿R 半径切线方向与垂直方向夹角即为飞机偏离角α, 通过数学建模计算飞机偏离角度α,具体见图3。
采用此模型进行实例计算举例: 飞机滑行速度15节,跑道宽45 米;飞行机组记录飞机直线滑行时间15秒后飞机偏离跑道中轴线距离约占跑道1/8。 带入公式计算得出偏离角度α=0.6°; 实际飞机调整0.5°后可保持直线滑行。 对比此模型计算角度与实际验证角度差距较小,比较符合实际前轮转弯偏转情况。
综上3 种建模对比,第3 种“三轮车模型”最接近实际飞机转弯偏转情况, 通过数学计算得出的偏离角度与实际最相符。
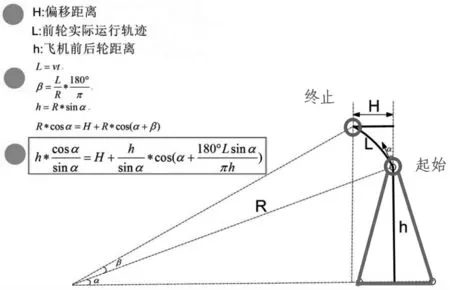
图3 三轮车模型
2.2 前轮转弯偏离角度计算
由于飞机转弯偏离模型建模和数学公式计算复杂, 不方便在实际生产过程中进行使用, 实际生产中最直接的参数是记录飞机滑行时间和读取飞机偏离距离跑道占比(即飞机偏移量),通过编制小程序(见图4),将带入数学公式,使用时仅输入常用参数即可得出计算结果,方便实际应用。

图4 飞机前轮偏转角度计算小程序界面
3 结语
经过以上建模分析对比,得出“三轮车模型”与实际飞机转弯情况最接近, 建模的准确性直接影响最终计算结果准确性, 对飞机前轮偏转问题的研究具有重要的意义;通过利用Excel 小程序对复杂建模公式进行二次转换,方便实际生产中使用。

