基于非线性优化的高温隔热服参数的研究①
,
(太原工业学院 理学系, 山西 太原 030008)
0 引 言
为了确保高温作业工作者安全,就需要为他们配备专用的工作服。耐高温的专用隔热服一般由三层织物材料构成,记为ⅠⅡⅢ层,其中Ⅰ层与外界环境接触,Ⅲ层内表面与皮肤之间存在的空隙层称为Ⅳ层。而传统隔热服生产企业采用的服装厚度设计参数算法复杂[1,5],人性化查,用户可选种类少,难以选到性价比高,又隔热效果好的产品。通过对隔热服热传导效果的分析,对厚度参数的选取做了优化处理,在结合文献4中MATLAB算法的实现,得到了简洁实用的定参法。
1 研究方法及过程
在现阶段各层常采用的材料参数如下表:
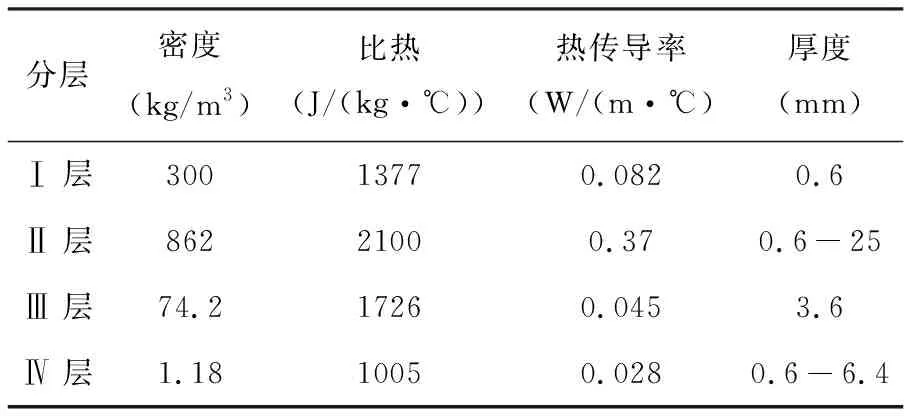
表1 高温隔热服参数表
从表中可知:在选定各层材料的基础上,第Ⅱ、Ⅳ层厚度的选取对服装隔热性能的影响尤为重要。为了把各层厚度对隔热影响的效果量化,先设计如下实验。将体温控制在37℃的假人放置在75℃高温环境中,给其配备Ⅱ层厚度为6mm、Ⅳ层厚度为5mm的工作服,设定工作时间为90min。测量假人皮肤表层的温度,发现其在16s开始升温,274s时温度达到44℃,1645s达到稳态温度48.08℃.考虑到隔热服的长度和宽度远大于它的厚度,所以将其近似看做平面处理,建立如下一维热传导模型。
对模拟各层的温度传递过程采用杆传热模型,假设它在同一截面上的温度是相同的,热交换发生在杆的表面和其周围介质,并服从规律[2]:
dQ=k1(u-u1)dSdt
其中密度为ρ,比热为c,热传导系数为k,温度为u
取层中的任意一段(x1,x2),从时刻t1到时刻t2热量的增加量为:
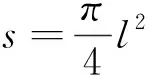
流过(x1,x2)侧面的热量与周围介质发生的热交换量为:
根据能量守恒定律Q1=Q2-Q3,以及x1,x2,t1,t2的随机性得:
其中
下面将热传导的方程:
离散以后得到:
为了确保上述差分式是稳定的,就需要使0 选择具有所需次数偏微商的函数u(x,t),满足上述方程和初始条件: u(x,0)=φ(x),0 边值条件: u(0,t)=u(l,t)=0,0tT 假定φ(x)在相应区域内光滑,并在x=0,l满足相容条件,使上述问题有且仅有唯一充分光滑的解。 计算步骤如下: (1)选定初始点X0和给定的要求ε>0,k=0; (3)在X(k)处沿方向P(k)做一维搜索得X(k+1)=Xk+λkPk,令k=k+1,返回第二步,直到求得最优解为止.可以求得[3] 可得:a1=0.000445532,a2=0.000452103,a3=0.000592767,a4=0.004859012 下面为其添加限制条件,当环境温度取为65℃、Ⅳ层的厚度为5.5 mm时,确定Ⅱ层的最优厚度,确保工作60min时,假人皮肤外侧温度达到稳态温度不超过47℃,且超过44℃的时间不早于55min[4]。 T|x>h447,t60,t|T≥445,T|x=0=65, h4=5.5,h2∈[0.6,25],h4∈[0.6,6.4] 采用Richardson差分形式,设定t和x的步长来求解这个优化问题,这里取0.01和0.1作为步长。 通过编程计算,可以得到如下结果,最佳厚度范围为[9.21,10.30],误差小于0.01,满足所需的要求,为了方便作业让总重量尽量减轻,由此选取9.21作为第Ⅱ层的厚度值。 若把工作时长设定为30min时,假人皮肤外侧温度达到稳态温度不超过47℃,且超过44℃的时间不早于25min时,第Ⅱ、Ⅳ层厚度均为变量[5] 需要得出厚度函数f(x)极小点的初始值X(0),按某种规律计算出一系列的X(k)(k=1,2,…),点阵{X(k)}的极限X*就是f(x)的一个极小点。 检验{X(k)}是否收敛与最优解,通过给定的精度ε>0,判断是否||f(Xk+1)||ε。 当用迭代法求函数的极小点时,常常用到一维搜索,即沿某一已知方向求目标函数的极小点值。 计算步骤如下: (1)对任意初始点X(1)∈En和向量P(1)=-f(X(1)),取k=1; X(k+1)=Xk+λkPk,λk=minf(X(k)+λkP(k))= (3)令k=k+1;返回(2) 为进一步改进模型,取环境温度为80℃时,探讨Ⅱ层和Ⅳ层的最优厚度,使之确保工作30分钟时,假人皮肤外侧温度达到稳态温度不超过47℃,且超过44℃的时间不早于25min。根据已知T|x>h447,t30,t|T≥445,T|x=0=80其中h2∈[0.6,25],h4∈[0.6,6.4] 利用Richardson差分形式,设定t和x的步长来求解这个优化问题,这里取0.001和0.01作为步长。 通过编程计算,可以得到如下结果, Ⅱ层最佳厚度范围为[11.69,13.80],Ⅳ层最佳厚度范围为[5.26,6.22],误差小于0.01,符合的要求,为了总重量尽量减轻,由此选取11.69和5.26分别作为第Ⅱ层和第Ⅳ层的厚度。 建立的热传导模型具有思维条理化,逻辑化,简明化的特征并且更贴近实际,得出的数据真实有效。建立了算法分类体系,有一定的容错能力,而且在得出大量数据之前,优化模型使得预测结果更具准确性和科学性。由于在一些数据处理中,因未考虑到热损等因素,导致结果存在一定的误差。 在热传导问题上,要综合考虑各种不同因素决定采用差分法求解偏微分方程,通过分析出各个因素的比例得到传导作用的优先顺序,由此得到温度场分布。从数理统计分析、实际环境和计算结果多方面因素可得,该模型基本上满足了实际要求。但实际情况与模型存在差异,该模型还有很大的优化空间。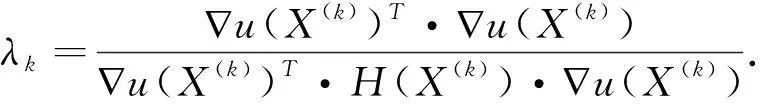
3 研究结果
3.1 当隔热服给定Ⅰ、Ⅲ、Ⅳ层,第Ⅱ层厚度的最优取法
3.2 当隔热服给定Ⅰ、Ⅲ层,第Ⅱ、Ⅳ层厚度的最优取法
4 结 语
4.1 模型的优缺点
4.2 模型的推广

