基于VSM与图像统计的多聚焦图像融合
李昌兴, 武 洁, 惠莉萍
(1. 西安邮电大学 理学院,陕西 西安 710121;2. 西安邮电大学 通信与信息工程学院,陕西 西安 710121;3. 西安科技大学 理学院,陕西 西安 710054)
图像融合是将一个场景的两个或两个以上源图像的显著特征融合到一幅融合图像的重要技术,为图像分析以及目标识别等应用提供了非常有价值的信息[1]。多焦点图像融合是融合使用不同的相机设置拍摄的同一场景中不同目标分别聚焦的多幅图像,形成一幅各个目标都清晰聚焦的新图像[2]。图像融合技术已广泛地应用于计算机视觉和计算机图形、医学影像、数码摄影、显微成像以及刑侦现场图像处理等应用领域。
目前,基于多尺度分析的融合算法受到的关注较多,如有能量压缩和多分辨率性质的小波变换[3]使融合后的图像结合了边缘及纹理等重要特征;基于提升小波变换[4]的方法,以融合图像的视觉质量和性能指标为代价减少了计算量;剪切波变换[5]解决了小波变换中块状效应的问题,并有效地提高了运算速率,但是,在离散化过程中,下采样的操作使其失去了平移不变性,在图像去噪和图像融合时可能在奇异点附近产生伪布吉斯现象[6];基于各向异性扩散(anisotropic diffusion, AD)[7]的融合方法是通过二阶偏微分方程实现的,对图像的均匀区域进行各向同性平滑,同时保持非各向同性区域,融合图像在平滑过程中模糊了边缘容易受到块状或伪影效应的影响,从而可能导致计算机视觉中检测到虚假物体[8];基于引导滤波的加权平均图像融合算法[9]有效地避免了伪影效应,但视觉显著特征不能被拉普拉斯算子生成的显著图表示出来,并且因考虑多方向分解,致使图像部分细节信息丢失;基于交叉双边滤波器(cross bilateral filter, CBF)[10]的融合方法结合图像的灰度相似性和相邻像素的空间邻近度获取滤波器内核,再对图像进行平滑,融合后的图像容易产生梯度反转伪像,且实现时间相对较长;基于四阶偏微分方程(ffourth order partial differential equations, FPDEs)[8]的融合方法避免了块状效应的影响,在边缘信息保留和图像平滑之间能更好的平衡。
针对以上多聚焦图像融合方法存在块状、伪影效应,图像细节信息失真等问题,本文拟提出一种将视觉显著性映射融合规则与图像统计相结合的融合策略。分别使用FPDEs和CBF对源图像进行多尺度分解获取近似层和细节层;对近似层采用基于视觉显著性映射(visual saliency map, VSM)[11]的融合方法提取图像的显著结构、区域和目标,用以减少融合图像的对比度损失,获得更好的整体视觉效果;细节层采用图像统计的融合规则,自适应地找到细节图像的最佳权重进行合并;对处理后的近似层和细节层通过线性组合的方式得到融合后的图像。最后,将本文方法分别与基于离散余弦变换(DCT)[12]、基于离散余弦谐波小波变换(DCHWT)[13]、基于主成份分析(PCA)[14]、基于四阶偏微分方程(FPDEs)[15]、基于交叉双边滤波器(CBF)[10]融合方法的实验结果进行比较以验证所提方法的效果。
1 多尺度图像分解
1.1 基于FPDEs的多尺度分解方法
图像可视为一个连续的对象,通常对图像进行无限小的迭代操作。为了避免块状效应的影响,在边缘信息保留和图像平滑之间能更好的平衡,本文采用基于四阶偏微分方程(fourth order partial differential equations, FPDEs)[8]的融合方法。
假设一个平面图像是能量函数Eu的全局极小化,则定义在Ω上的连续图像函数空间中的能量泛函[16]为
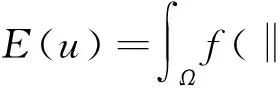
(1)
其中,Ω为图像的定义域,u为图像强度函数,2是拉普拉斯算子,‖·‖表示绝对值,f(·)为非负的增函数。
为极小化能量泛函,FPDEs方法使用梯度下降的过程[8]如下
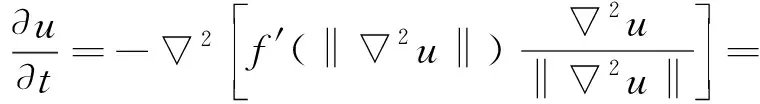
(2)
其中,t为时间,f′(s)=g(s)s,s为变量,g(·)为扩散系数,k是常量。
应用迭代法对偏微分方程(1)进行数值逼近,记为
(3)
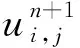
(4)
(5)
对源图像A和B分别经过FPDEs[15]边缘保留的分解过程获得近似层Aa(i,j)和Ba(i,j),分别记为
Aa(i,j)=FPDEs(A(i,j)),
Ba(i,j)=FPDEs(B(i,j))。
(6)
1.2 基于CBF的多尺度分解方法
基于交叉双边滤波器(Cross Bilateral Filter, CBF)[17]的融合方法先是结合其中一个源图像的灰度相似性和相邻像素的空间邻近度获取滤波器内核后,再对另一个源图像进行滤波处理,最后从源图像中减去相对应的滤波后的图像获取细节层图像。
假设源图像为A,利用双边滤波器计算源图像A的灰度相似性和相邻像素的空间邻近度以获取核函数,源图像A在像素x处的双边滤波器输出[10]为
(7)
式中σμ和ση分别是控制空间域和强度域中权重下降的参数,R(x)是x的空间邻域,‖y-x‖是y与x之间的Euclidean距离,ν是归一化常数,表示为
(8)
源图像B在像素x处的CBF输出[18]为
(9)
同理,可获得ACBF(x)。分别从源图像A和B中减去所对应CBF的输出获取源图像A和B,即可得到细节层图像,分别记为
Ad=A-ACBF,Bd=B-BCBF。
(10)
2 基于VSM与图像统计的融合规则
2.1 视觉显著性映射
一般情况下,多尺度分解方法为了减少计算量,致使分解级数受到限制,因此从源图像中获得的近似层保留了相当多的残余低频信息,使得融合图像的整体视觉反差较大。而传统的“平均”融合规则不能充分有效地利用这些低频信息,通常导致融合图像的对比度不足。视觉显著性映射是一种利用计算感知或认知技术定量预测视觉吸引力的图像分析方法[19],能有效地减少融合图像的对比度损失,获得更好的整体外观。构造VSM[11,20,21]的方法如下所述。
定义源图像I中α处的像素Iα的显著性值为
(11)
式中‖Iα-Ii‖是Iα与Ii之间的颜色距离度量,Ii的取值范围为[0,255]。扩展像素等级后,式(11)可以写为
SV(Iα)=‖Iα-I1‖+‖Iα-I2‖+
…+‖Iα-IN‖。
(12)
其中N表示图像I中像素总数。若两个像素具有相同的强度值,则对应的显著性值也相等,则式(12),可以写为
(13)
式中Mi表示图像中像素Ii的数量,L是灰度级数。通常情况下,SV(Iα)被归一化,且其取值范围为[0,1]。
同理,分别对源图像A和B使用上述VSM方法提取源图像的显著性图AV和BV,再用改进的平均融合规则将AV和BV与近似层Aa(i,j)和Ba(i,j)进行融合得到融合后的近似层图像,记为
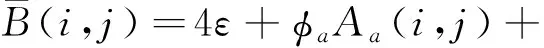
(14)
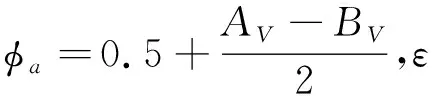
2.2 图像统计
基于图像统计的融合规则可以使用邻域的统计特性[22]自适应地决定权重,其主要思想是图像块的协方差矩阵的特征值取决于图像块中边缘的强度,从而为中心像素选择一个更佳的权重,使像素具有更清晰的邻域权值。鉴于此,本文采用图像邻域的统计特性自适应地找到细节图像的最佳权重。
通过在该像素点的周围取一个大小为w×w的窗口来计算图像中像素点(i,j)处对应的权重,主要是根据水平和垂直细节层强度寻找对应图像位置的最佳权重。
首先,假设图像块为矩阵K,将矩阵K的每一行作为观测值,每一列作为变量,其协方差矩阵为[23]
Dh(K)=E[(K-E[K])(K-E[K])T],
(15)
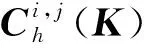
(16)
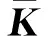
(17)
(18)
通过将水平和垂直这两个相应的细节层强度相加得到图像细节层系数的权重,记为
W(i,j)=βh(i,j)+βv(i,j)。
(19)
对细节层图像Ad(i,j)和Bd(i,j)分别采用图像统计的融合规则得到最佳权重WA(i,j)和WB(i,j),再与源图像进行加权平均得到融合后的细节层图像,记为
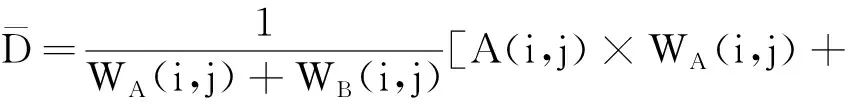
(20)
2.3 图像融合

(21)
2.4 算法流程及步骤
本文提出的多聚焦图像融合方法是将视觉显著性映射与图像统计特性的融合规则结合在一起,通过四阶偏微分方程(FPDEs)与交叉双边滤波器(CBF)多尺度分解的方法获取源图像的近似层和细节层,近似层采用基于视觉显著性映射(VSM)的融合规则,细节层采用图像统计的融合规则,再对处理后的近似层和细节层图像进行线性组合得到融合图像。算法流程如图1所示。
算法的具体步骤如下。
步骤1分别对源多聚焦图像A和B采用FPDEs的多尺度分解方法得到近似层图像Aa(i,j)和Ba(i,j)。
步骤2分别对源多聚焦图像A和B采用基于CBF的多尺度分解方法得到细节层图像Ad(i,j)和Bd(i,j)。
步骤3分别对源图像A和B使用VSM方法提出源图像的显著性图AV和BV。
步骤4对步骤1中获取的近似层Aa(i,j)和Ba(i,j)以及步骤3中得到的显著性图AV和BV采用加权平均的方法进行融合。
步骤5对步骤2中获取的细节层图像Ad(i,j)和Bd(i,j)采用图像统计的融合规则进行融合。
步骤6对步骤4和步骤5中获取的近似层图像和细节层图像进行线性组合得到最终的融合图像。
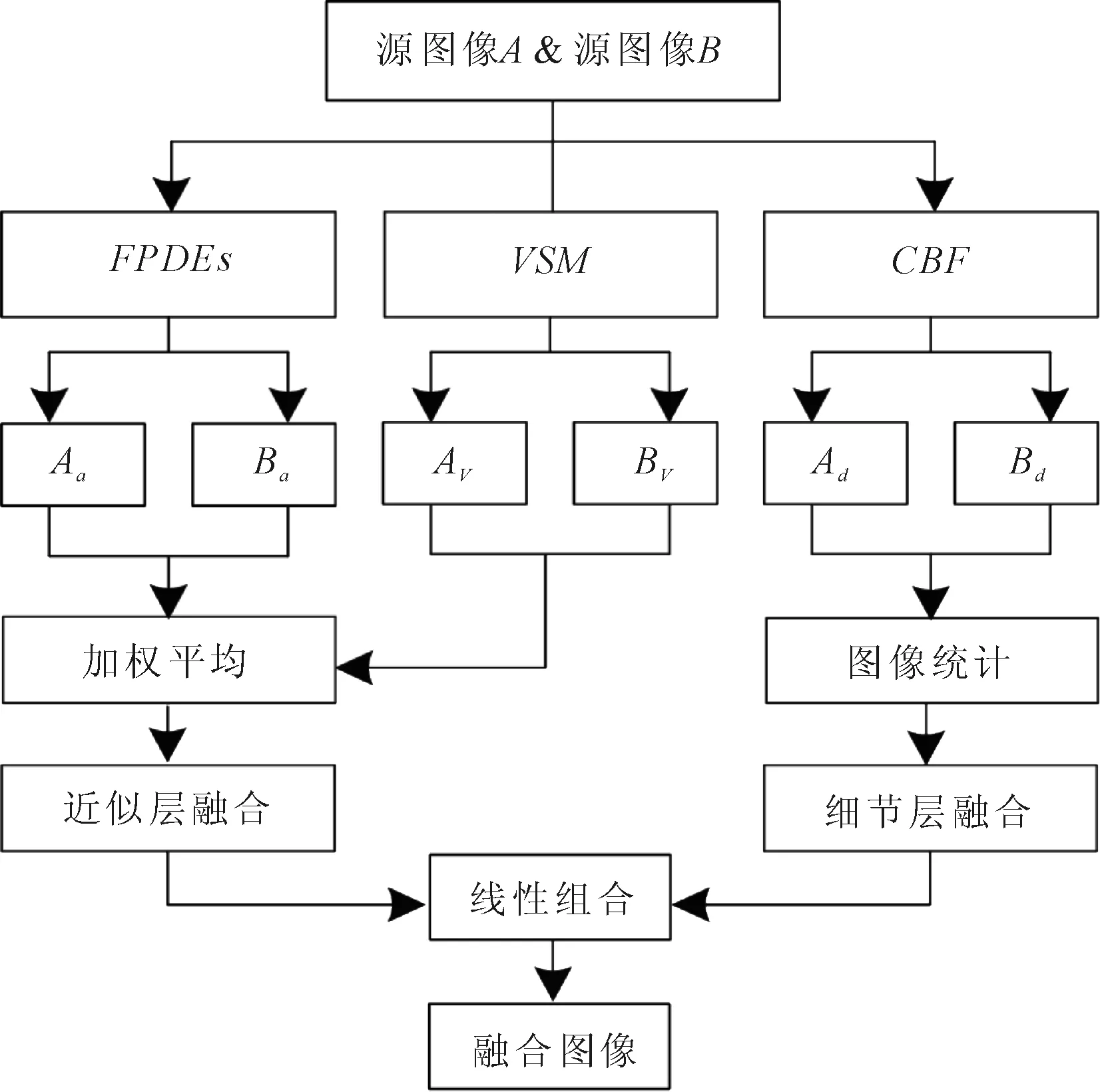
图1 融合算法流程图
3 实验结果与分析
为了验证文中提出方法的有效性,选择不同聚焦水平的两组源图像进行实验,分别为“Clock”图像数据集和“Pepsi”图像数据集,如图2所示。

图2 两组待融合源图像
实验运行环境为中央处理器为Intel(R) Core(TM)i3-3217U,1.8GHz,安装内存为4GB的PC机,64位Win7操作系统,Matlab版本为Matlab 8.3.0.532(R2014a)。从主观视觉和客观指标上对本文方法与文献[12-15]及文献[10]中的方法进行评估比较。两组实验中不同融合方法的融合结果详细显示了融合图像的视觉质量,如图3所示。为便于分析融合图像的结果,其部分区域被放大。

图3 两组图像不同融合结果比较
3.1 主观评价
在第一组以“Clock”为源图像的结果图中,由图3(a)可以看出文献[12]的融合方法存在锯齿效应,特别是小时钟的上边缘标出的部分,信息失真较严重。图3(b)可以看出文献[13]方法的融合图像背景中产生了块状伪影。图3(c-d)可以看出文献[14-15]方法的融合图像对比度不高而且存在阴影,导致视觉效果模糊,特别是小钟表中的数字“6”。图3(e)可以看出文献[10]的方法产生了梯度反转伪像。
在第二组以“Pepsi”为源图像的结果图中,由图3(a)可以看出文献[12]的融合方法在“ES Magnifier Quality”词汇的上边沿均存在阴影,在字符“P”区域中有块状伪影。文献[13]方法的融合结果中存在块状效应,而文献[10]方法的融合图像存在梯度反转伪像。图3(c-d)可看出文献[14-15]方法的融合图像对比度相对较低并存在阴影,导致视觉上看到的部分区域较模糊。与以上方法相比,两组实验中图3(f)的融合图像避免了“块状伪影”的现象,减少了图像对比度的损失,图像的亮度、以及视觉效果更佳。
3.2 客观评价
考虑到人眼视觉效果对融合图像的评价带有一定主观色彩,为了对融合后的图像进行更加客观的分析,本文分别采用图像的平均像素强度(API)、标准差(SD)、平均梯度(AG)、信息熵(H)、相关系数(Corr)、空间频率(SF)和相互特征信息(FMI)的指标[22]等进行评估。
两组实验所获得的融合图像的性能指标大小,分别如表1和表2所示。
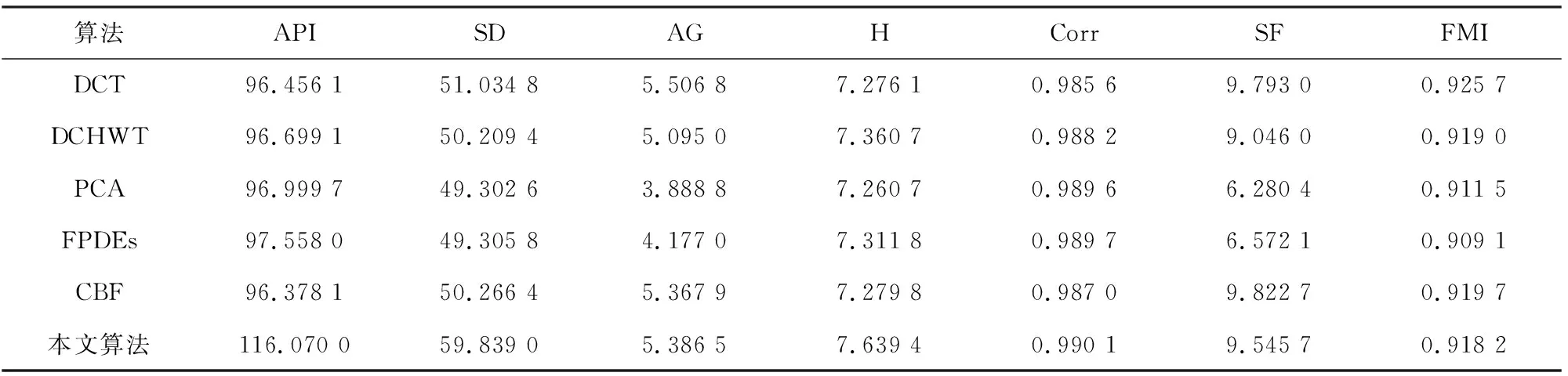
表1 不同融合方法的客观评价(第一组“Clock”实验)
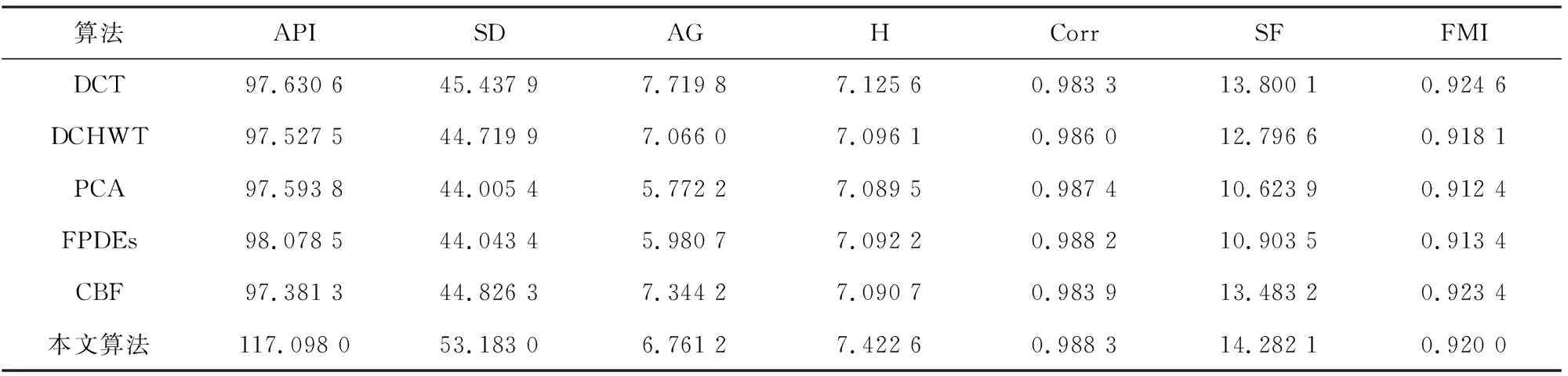
表2 不同融合方法的客观评价(第二组“Pepsi”实验)
从表1中以“Clock”为源图像的数据中可以看出,本文算法的融合结果在平均像素强度、标准差、信息熵、相关系数4个质量指标上比文献[12-15]及文献[10]中的更高,说明得到的融合图像的平均亮度更高,包含的源图像中的信息更加丰富,融合图像与源图像的相关性更高;从表2中以“Pepsi”为源图像的数据中可以看出,本文算法的融合结果在平均像素强度、标准差、信息熵、相关系数和空间频率5个质量指标上都比文献[12-15]及文献[10]中的融合算法更高,说明融合图像的亮度更高,包含源图像中的信息更加丰富,与源图像的相关性更高,区域整体信息也更多。因此,可以说明本文方法的融合图像在平均亮度、信息丰富度上更为优越,与源图像的相关性更高,图像的质量更好,这与主观评价一致。
4 结语
针对多聚焦图像融合问题,提出一种视觉显著性映射融合规则与图像统计相结合的融合方法。该方法利用FPDEs和CBF的多尺度分析方法分别从源图像中获取近似层和细节层,近似层采用一种基于VSM的加权平均技术融合,细节层采用图像统计的融合方法,将处理后的近似层与细节层图像进行线性组合得到融合图像。实验结果表明,该方法能够有效地将源图像的有用信息转移到融合图像中,并且相对减少了图像融合过程中的对比度损失和伪像现象,融合图像的平均像素强度、标准差、信息熵及相关系数等指标都有显著的提高。本文方法是否适合多聚焦彩色图像融合将是值得研究的问题之一。

