裂缝性地层溢流侵入动态规律研究
何世明,刘 森,赵转玲,汤 明,李 恒,邓富元
(1.油气藏地质及开发工程国家重点实验室(西南石油大学),四川成都 610500;2.中石化中原石油工程有限公司钻井工程技术研究院,河南濮阳 457001)
对于以碳酸盐岩为代表的裂缝性储层来说,由于其安全窗口极小,在钻井过程中极易发生溢流或漏失。了解发生溢流时流体从地层流入井筒的过程是研究环空多相流的基础,弄清不同条件下的溢流机理有助于更好地模拟环空流体运移情况。目前,关于裂缝性地层溢流机理的研究主要有试验探究、理论模型分析和模拟分析等3种方式。张志等人[1-3]研制了可视化试验装置,通过室内试验,分析了负压溢流、正压漏失和重力置换溢流的发生条件;R.Majidi等人[4-6]建立了单条裂缝模型,模拟了井下溢流、漏失、重力置换情况;舒刚[7]则进一步用模拟软件证实了重力置换溢流规律。但是,目前针对裂缝性地层欠平衡溢流机理的研究尚不充分,多数是沿用渗透性地层渗流理论。因此,有必要建立裂缝性地层欠平衡溢流模型,探究其溢流机理,并在此基础上分析天然条件下裂缝闭合对溢流规律的影响。为此,笔者建立了考虑裂缝闭合情况的单条裂缝欠平衡溢流侵入动态模型,采用有限差分法对其进行了求解,分析了影响因素及影响规律,以期为建立更加完善的裂缝性地层溢流、漏失模型提供依据。
1 模型的建立
1.1 裂缝微观闭合模型
假设条件:1)裂缝为径向单条裂缝;2)裂缝面微凸体受压满足赫兹弹性接触定律;3)各方位水平地应力相等。
地层条件下,裂缝内压力满足有效应力定理[8]:
σn=σ-pp
(1)
式中:σn为裂缝有效应力(由微凸体承担),MPa;σ为作用于裂缝面的正应力,MPa;pp为裂缝内流体压力,MPa。
考虑裂缝倾角、水平应力和垂向应力[9],式(1)可改写为:
式中:ρm为上覆岩层密度,kg/m3;H为裂缝所在深度,m;ν为岩石泊松比;θ为裂缝倾角,(°)。
采用B&S模型描述裂缝闭合[10],裂缝上下两面皆为微凸体,粗糙平面高度随机分布,将上下两个粗糙平面合成为一个粗糙平面与一个光滑平面(见图1,图1中:z为复合接触面上的微凸体高度,mm;z1,z2分别为原始接触面两面上微凸体高度,mm),认为接触发生在合成表面与光滑平面之间。微凸体为半球体形状,满足赫兹弹性接触理论,如图2所示(图2中:R为微凸体期望半径,mm;Δh为法向变形量,mm;b0为裂缝初始开度,mm;δ为裂缝闭合量,mm)。
根据赫兹弹性接触理论[11],裂缝有效应力与裂缝闭合量之间的关系为:

图1 B&S模型复合接触示意Fig.1 Schematic of composite contact in B&S model
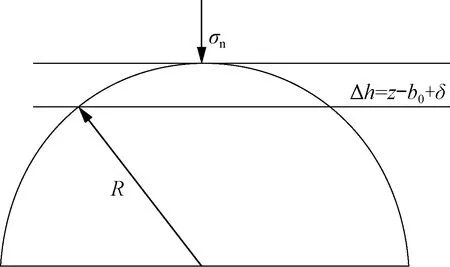
图2 赫兹弹性接触示意Fig.2 Schematic of Hertz elastic contact
式中:αd为微凸体密度,mm-2;Ψ为剪切应力校正因子;E′为岩石有效弹性模量,GPa;φ为裂缝面微凸体高度分布函数。
假设裂缝上下表面岩石性质相同,裂缝面微凸体高度分布一般满足正态分布[12],则:
(4)
(5)

1.2 裂缝气体流动模型
假设条件:1)径向平板裂缝中心为井筒,裂缝属于中—大裂缝;2)裂缝内流体仅为天然气,裂缝空间封闭,无外界气源供给,也不考虑基质系统向裂缝供气;3)气体流动满足高速非达西流动条件;4)溢流期间井底流动压力恒定;5)不考虑气体重力作用;6)气体流动过程中温度恒定。
基于以上假设,根据质量守恒定律,可得气体运动连续性方程:
(6)
式中:r为径向距离,m;v为气体流动速率,m/s;ρ为气体密度,kg/m3。
气体为高速非达西流动,满足二项式运动方程[13],其运动方程为:
(7)
式中:p为缝内气体压力,Pa;μ为天然气黏度,Pa·s;K为裂缝等效渗透率(满足立方定律),m2;β为惯性系数,m-1。
惯性系数采用A.Firoozabadi等人[14]提出的经验公式计算:
(8)
由于存在裂缝面微凸体,气体流动通道等效开度应小于裂缝几何开度,计算井底溢流总量时也会用到裂缝水力等效开度。等效开度采用R.W.Zimmerman等人[15]给出的公式计算:
(9)
式中:be为裂缝水力等效开度,mm;b为裂缝几何开度,mm;c为裂缝接触面积比(裂缝面相互接触的面积与裂缝面总面积之比)。
1.3 考虑裂缝闭合情况的溢流侵入模型
将裂缝微观闭合模型与裂缝气体流动模型联立,便得到考虑裂缝闭合情况的单条裂缝欠平衡溢流侵入模型。
2 模型的求解
考虑裂缝闭合条件的单条裂缝欠平衡溢流侵入模型是一维瞬态模型,难以获得解析解。因此,采用有限差分法对其进行数值模拟。
2.1 差分方程
为方便求解,引入气体压缩系数:
(10)
式中:C为气体压缩系数,Pa-1。
将式(7)、式(10)代入式(6),得到:
(11)
其中,ζ为二项式紊流修正系数,计算公式为:
(12)
将式(11)展开,可得:
(13)
式(13)的差分格式为:
(14)
式中:rw为井筒半径,m。
井底流压pwf是常数,可确定内边界条件。裂缝系统封闭,无外界气体供给,因此外边界条件为:
(15)
裂缝钻开之前裂缝内压力处处相等且等于裂缝初始压力pi,得出初始条件:
p(0,r)=pi
(16)
2.2 求解步骤
裂缝微观闭合模型与裂缝气体流动模型的结合点是裂缝内气体压力。随着缝内气体逐渐流出,裂缝压力逐渐降低,裂缝有效应力逐渐增大,导致微凸体被压缩,裂缝渐渐闭合,开度减小,而裂缝闭合又会导致缝内气体被压缩,压力有所上升,形成耦合关系。在求解时,先算出该时刻的压力分布,再联立闭合方程,耦合处理后得到新的压力分布,作为计算下一时刻压力分布的已知条件。计算流程如图3所示。
算出任意时刻任意空间的压力、速率等参数后,对每一个时刻的溢流量进行求和运算。溢流总量计算公式为:
(17)
式中:Q为井底溢流总量,L;v0为气体从地层流至井筒时的速率,m/s。
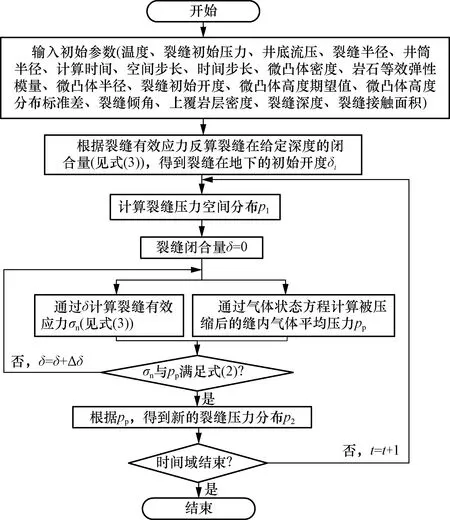
图3 裂缝压力分布计算流程Fig.3 Calculation flow of fracture pressure distribution
3 溢流规律及影响因素分析
利用上述所建模型,分析了考虑裂缝闭合和不考虑裂缝闭合两种情况下的溢流规律及其影响因素。若文中未特别说明,以下参数的取值分别为:地层温度373 K,裂缝深度4 000 m,井底流压55 MPa,井筒半径0.075 m,岩石等效弹性模量19 GPa,微凸体密度10个/mm2,微凸体半径0.1 mm,裂缝倾角0°,上覆岩层密度2.5 g/cm3,岩石泊松比0.3,裂缝接触面积比0.4。
3.1 不考虑裂缝闭合时的溢流规律及影响因素
与渗透性地层相比,气体在裂缝性地层中的流动通道大,流动速率快,导致气体在裂缝中的流动规律与渗透性地层不同。根据所建模型,分析了裂缝开度、裂缝半径和压差对溢流规律的影响。
3.1.1 裂缝开度的影响
假设裂缝压力与井底流压的差为2 MPa,裂缝半径为20 m,分别分析裂缝开度为0.1,0.3,0.5,0.7和0.9 mm时,裂缝平均压力及溢流量随时间的变化规律,结果如图4所示。
由图4(a)可知,随着溢流时间的增长,裂缝平均压力下降速度先快后慢。随着裂缝开度增大,曲线逐渐由近似线性关系发展到越来越下凹,说明裂缝压力下降越来越快,原因是裂缝开度越大,等效渗透率越大,气体流动的惯性系数越小,流动阻力越小,流动速率越快,裂缝压力加速衰竭。

图4 不考虑裂缝闭合时不同开度下裂缝平均压力与溢流量变化规律Fig.4 Variation laws of fracture average pressure and overflow volume under different opening degrees without considering the closure
由图4(b)可知,溢流量随着时间的增长而下降,在最初的2 s内溢流量迅速下降,之后呈近似线性关系降至约为0。随着裂缝开度的线性增大,初始溢流量增加越来越快;随着时间的增长,裂缝开度大的溢流量衰减较快,很快降至0。
图4说明裂缝开度对溢流产生重要影响。随着裂缝开度线性增长,气体初始流动速率不断加快,压力衰减也加快,越来越呈现裂缝溢流的规律;裂缝开度越小,越来越呈现渗透性地层流动规律。模拟条件下,在裂缝开度为0.1 mm的裂缝中溢流衰竭时间约10 min,而在裂缝开度为0.9 mm裂缝中仅约52 s。由此可见,在钻遇开度较小(微米级)的裂缝(组)地层时,气体溢流持续时间较长,溢流速率较小,有利于地面发现后采取措施;但在钻遇开度较大的裂缝、溶洞地层时,溢流将会在较短时间内结束,速率较大,可能地面尚未发现时就已结束,无法采取相应措施,并且随着大量气体向上运移、膨胀,可能产生严重的井涌甚至井喷,对井控安全造成巨大威胁。
3.1.2 裂缝半径的影响
假设裂缝压力与井底流压的差为2 MPa,裂缝开度为0.8 mm,分别分析裂缝半径为1,5,10,15,20,25和30 m时,裂缝平均压力及溢流量随时间的变化规律,结果如图5所示。

图5 不考虑裂缝闭合时不同半径下裂缝平均压力与溢流量变化规律Fig.5 Variation laws of fracture average pressure and overflow volume under different radius without considering the closure
由图5(a)可知,随着溢流时间的增长,裂缝压力下降的速度先快后慢。随着裂缝半径的增大,裂缝压力衰减越来越慢,钻遇半径较小的裂缝时气体释放将在10 s内结束。溢流量随时间的变化规律与裂缝平均压力随时间的变化规律基本一致。
由图5(b)可知,随着裂缝半径增大,初始溢流量恒定。裂缝半径越大,裂缝内储存的气体量越多,井筒附近的气体流出后裂缝远端的气体能够及时补给,整体的平均压力衰减也更慢。
3.1.3 压差的影响
假设裂缝开度为0.8 mm,裂缝半径为20 m,分别模拟压差为1,2,3,4和5 MPa时,裂缝平均压力及溢流量随时间的变化规律,结果如图6所示。
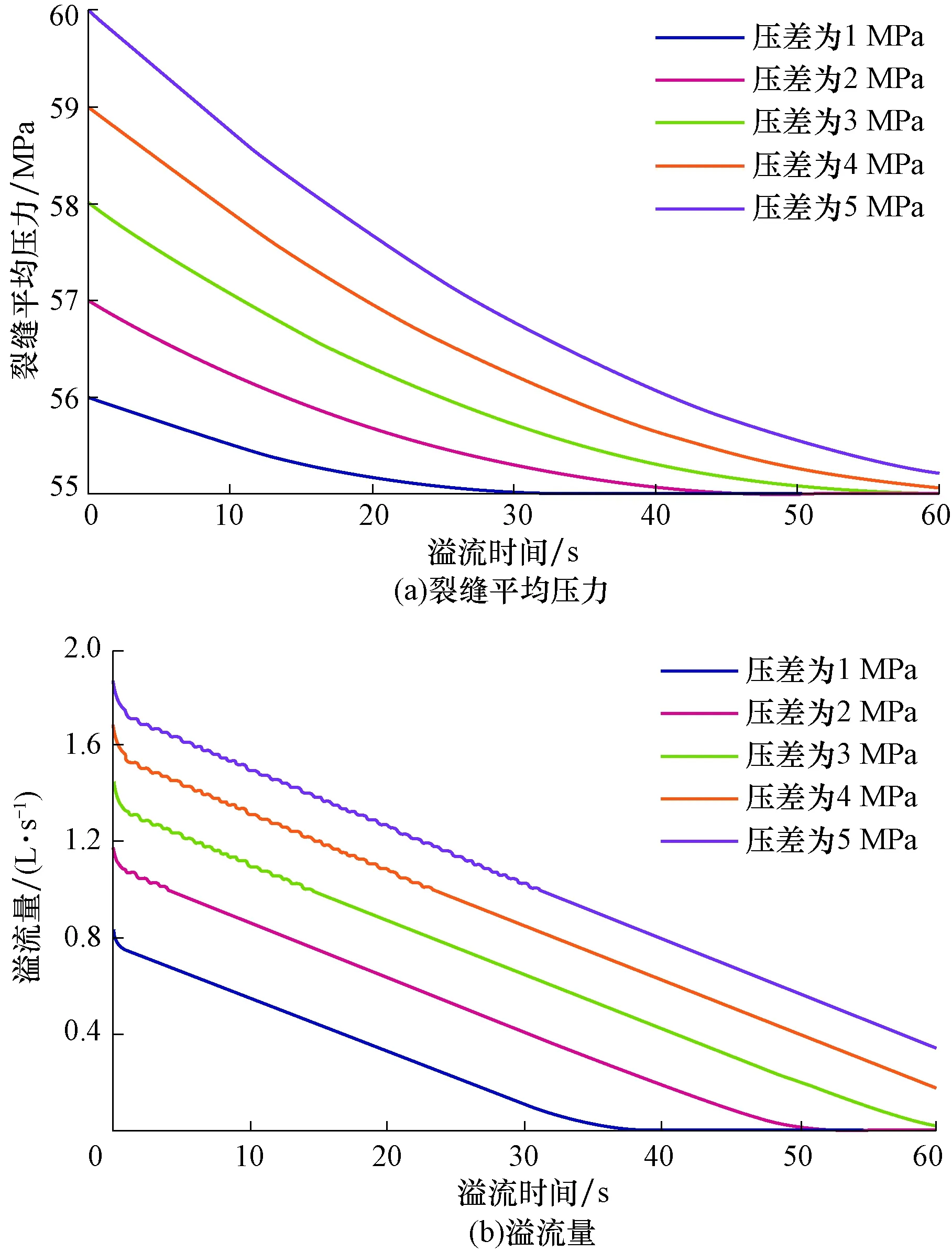
图6 不考虑裂缝闭合时不同压差下裂缝平均压力与溢流量变化规律Fig.6 Variation laws of fracture average pressure and overflow volume under different pressure difference without considering the closure
由图6(a)可知,裂缝平均压力降低速度随时间先快后慢,压差越大,同一时间段内压力衰减的幅度越大,流出的气体量越多;由图6(b)可知,随着压差增大,溢流量逐渐增大,但增幅依次减小,满足高速二项式渗流规律。
3.2 考虑裂缝闭合时的溢流规律及影响因素
在自然条件下,随着气体从裂缝流动至井筒,裂缝压力减小,有效应力增大,将会压缩裂缝表面的微凸体,从而压缩裂缝空间,导致溢流情况更加趋于恶劣。因此,分析了裂缝闭合时压差、裂缝开度对溢流规律的影响。
3.2.1 压差的影响
假设裂缝开度为0.8 mm,裂缝半径为20 m,分别模拟压差Δp为1,2和3 MPa条件下考虑/不考虑闭合情况时的裂缝平均压力和溢流量变化规律,结果如图7所示。

图7 不同压差下裂缝平均压力与溢流量变化规律Fig.7 Variation laws of fracture average pressure and overflow volume under different pressure difference
从图7(a)可以看出,考虑裂缝闭合与不考虑裂缝闭合两种情况下,裂缝平均压力具有相同的变化趋势。考虑裂缝闭合时裂缝压力衰减较慢,28 s后压差为2 MPa;压差3 MPa时,考虑裂缝闭合时的压力曲线甚至在不考虑裂缝闭合的压力曲线之上。抽取压差为2 MPa时的压力曲线,研究不同溢流时间下裂缝压力随径向距离的变化趋势(见图8),可知在压力衰竭之前,随着时间的增长,同一位置下考虑/不考虑裂缝闭合的裂缝压力差值越来越大。同时,压差越大,同一时刻下考虑/不考虑裂缝闭合时的裂缝压力差值也越大。
由图7(b)可知,考虑裂缝闭合时溢流量的变化趋势与裂缝压力变化趋势相似,但曲线斜率绝对值更小,说明溢流量衰减更慢,原因在于裂缝闭合后压缩气体,使得裂缝内气体压力尽可能地保持在较高值,而压力值较高意味着与井底流压的差值始终较大,所以气体流速较大,溢流量较大。经计算,压差为2 MPa时,考虑裂缝闭合时的溢流总量约为不考虑裂缝闭合时的1.7倍。

图8 不同时刻裂缝压力的径向分布Fig.8 Radial distribution of pressure at different times
3.2.2 初始裂缝开度的影响
假设压差为2 MPa,裂缝半径为20 m,分别模拟初始裂缝开度为0.3,0.5和0.7 mm时考虑和不考虑裂缝闭合情况下裂缝的平均压力和溢流量变化规律,结果见图9。

图9 不同开度下裂缝平均压力与溢流量变化规律Fig.9 Variation laws of fracture average pressure and overflow volume under different opening degrees while considering the closure
由图9(a)可知,考虑裂缝闭合时3种裂缝初始开度的压力大于同时刻不考虑裂缝闭合时的压力;随着初始裂缝开度的增大,同一时刻下,考虑与不考虑裂缝闭合时的裂缝压力差值逐渐减小,是因为初始开度小的裂缝其缝宽减小幅度大于初始开度大的裂缝。由图9(b)可知,裂缝的闭合延长了溢流衰竭时间,溢流总量也有所增大。
由此可见,考虑裂缝闭合情况的模型显示裂缝的压力降低、流量减小更慢,同一时间内的溢流量更多,衰竭时间更长。分析认为,其原因是裂缝闭合之后,裂缝空间减小,会对其本身因气体流出而造成的压力降低起到缓解作用,使压力尽可能保持在较高的水平,裂缝闭合空间的气体也最终流入井筒。因此,由考虑裂缝闭合情况的模型得到的溢流表现出速率更快、总量更多、时间更长的特点。
4 结论与建议
1) 通过建立裂缝气体流动模型,模拟了钻遇裂缝、溶洞时的溢流侵入动态规律,研究发现钻遇裂缝、溶洞时会发生短时间剧烈的溢流过程,裂缝压力、溢流量的变化与裂缝开度、裂缝半径和欠压值有关。
2) 自然条件下,随着裂缝中气体流入井筒,裂缝会产生闭合,这种闭合一方面受气体流动的影响,另一方面也会影响气体流动。在裂缝气体流动模型的基础上,联立裂缝微观闭合模型,将裂缝的闭合与气体从裂缝流至井筒的过程耦合起来,揭示了自然条件下的溢流规律,与不考虑裂缝闭合情况的模型相比,考虑裂缝闭合后得到的裂缝压降更慢,溢流速率更快、溢流总量更多、溢流持续时间更长。
3) 所建立的考虑裂缝闭合条件的单条裂缝欠平衡溢流侵入模型,将裂缝闭合与裂缝内流体运动进行了耦合,对今后裂缝性地层溢流、漏失模型的建立具有一定指导意义。但综合而言,本文所建模型的假设条件较为理想化,未考虑外界气源的供给与基质对裂缝的供气情况,建议进一步研究完善。

