Influence of control strategy on stability of dual-spin projectiles withfixed canards
Yu Wang,Xiao-ming Wang,Ji-yan Yu
Nanjing University of Science&Technology,School of Mechanical Engineering,210094,Nanjing,People's Republic of China
Keywords:Dual-spin projectile Fixed canards Control strategy Flight stability
A B S T R A C T Existing literature has shown that the control force at the nose could cause dynamic instability for controlled projectiles.To lower the adverse impact on the dual-spin projectile with fixed canards under the premise of meeting guidance system requirements,the influence of control moment provided by a motor on the flight stability is analyzed in this paper.Firstly,the effect of the rolling movement on stability is analyzed based on the stability criterion derived using the Hurwitz stability theory.Secondly,the evaluation parameters combining the features of different control periods that could assess the variation of stability features after the motor torque are obtained.These effective formulas are used to indicate that,to reduce the flight instability risks,the stabilized rolling speed of roll speed keeping period should be as small as possible;the variation trend of motor torque during the rolling speed controlling period and the roll angle of the forward body during roll angle switching period are recommended corresponding to the projectile and trajectory characteristics.Moreover,detailed numerical simulations of 155 mm dual-spin projectile are satisfactory agreement with the theoretical results.
1.Introduction
Undoubtedly,low collateral damage and high strike precision are the increasing requirements of the modern and future battlefield.To this purpose,interest in retrofitting the large stockpile of existing conventional munitions to possess trajectory correction capability has led to the development of several programs[1-6]over the past four decades.Because the extremely high spin rates of the spin-stabilized projectile will bring severe technical challenges for smart-weapon designers,the concept of roll-decoupled course correction fuse with canards was proposed.
Costelloetal.[7]developedadual-spinprojectilesevendegreeof-freedom(7DOF)dynamicmodelanddiscussedthedynamicand the gyroscopic stability by using projectile linear theoryapplicable for this projectile without canards.Wernert[8]studied the stabilityofcanard-guideddual-spinprojectilebyvirtueofalinearized model of the pitching and yawing motion.Zhu et al.[9]deduced a stability criterion for such a projectile utilizing the linear theory,Murphy's complex variable method and Hurwitz stability theory.Ollerenshaw[10]and Fresconi[11]analyzed the swerve response of spin-stabilized projectiles to control mechanism inputs,and demonstratedthatthephaseshiftoftheswerveresponseiscloseto 180°when the control mechanism is located near the nose of projectile.Chang[12]explored the dynamic response to control input by considering the coupled effect of canard control and gravity,and indicated that the phase shift may vary substantially with different deflection angles of canards during the process of guidance and control.Theodoulis et al.[13]analyzed the airframe stability for operating points of the flight envelop in terms of the quasi-linear parameter-varying model and presented a complete design concerning the guidance and autopilot modules for a class of spin-stabilized fin-controlled projectiles.Frank Fresconi[14]derived a guidance and control strategy based on flight dynamics that enables precision and trajectory shaping with reduced sensor and actuator needs.
The work here aims at the dual-spin projectile with two sets offixed canards[15](shown in Fig.1):a pair of spin canards(canards 1-3)and a pair of steering canards(canards 2-4).In a bank-toturn approach,steering is accomplished by stabilizing the forward body at the appropriate roll angle to create lift in a desired direction with the motor.Contrary to the extensive literature on several aspects regarding this projectile,such as general design,aerodynamics[16],dynamic response,flight stability and guidance,research on the influence of control strategy on the stability of the dual-spin projectile with fixed canards is,to the authors'knowledge,very limited.
This paper investigates the affecting laws of control moment onflight stability of a dual-spin projectile,which can provide a foundationforstructureandcontrollingplandesign.Thearticlebeginswitha descriptionofthedifferentialequationforthecomplexangleofattack utilizing the projectile linear theory and Murphy's complex variable method.Then the stability criterion and the influence of control moment on flight stability in different control periods are derived.Finally,numerical simulation results and concluding remarks are provided.
2.Stability analysis
For the sake of simplicity,a simplified 7DOF dynamic model whose general case was studied by Costello[7]is established based on the assumption that.
(1)The projectile is nearly aerodynamic symmetric and mass balanced;
(2)The composite center of mass locates on the longitudinal symmetry axis;
(3)Only the roll constrain moment is considered between the forward and the aft bodies;
The translational and rotational dynamic equations of motion are expressed in the fixed-plane frame as
Where˙φFP=-r tanθ.
The dynamic model of the dual-spin projectile with fixed canards is almost the same with that with cruciform canards other than the control force,control moment and the motor moment acting on the axis-direction.Referring to the model in Refs.[9]and[12],the control force and control moment of a dual-spin projectile due to fixed canards in the fixed-plane reference frame can be calculated by
The structure schematic of the dual-spin projectile and the moments on the longitudinal symmetry axis of the projectile are shown in Fig.2.The rolling moments come from the bearing Mrband motor Mmoare acting on the forward and aft body in the opposite direction.The roll damping moments MrdAand MrdFwhich can be calculated by equation(4)are acting on the aft and forwardbody respectively.CrdFhereisa negativenumber;CrdAhere is a positive number.In order to ensure the normal operation of the correction course fuse,a negative roll moment due to the spin canards(shown in equation(5))is acting on the forward body.
Substituting these moments into the dynamic equation(1),the rolling dynamic equations of the forward and aft parts are expressed in the fixed-plane frame
Corresponding to directions of these moments shown in Fig.2 and the dynamic equations shown as equation(6),CrdFis negative,and Crc,CrdAare positive.
The remaining rolling moment come from bearing Mrbis composed of the viscous damping and rolling friction.The moments acting on the axis-direction of projectile can be written as[7].
where the absolute value of normal force acting on the bearing|FN|is related to the axial force of the forward and aft part.
By using Murphy's method[17]and the linear theory for projectile,the differential equation of complex angle of attack can be written as
Where
Linearized at the equilibrium point of equation(8),Φcould be estimated as-iξetan θe[β′′+ (H-2g*-iP)β′],so the equation of complex angle of attack can be rewritten as
Where ξ = β-iα;ε=0.5 tan θe.By the coefficient freezing way,the equilibrium point of equation(8)can be expressed as
By comparison with the complex angle of attack of a dual-spin projectile with cruciform canards deduced in Ref.[9],equation(9)has a good consistency with that of cruciform canards on the form and difference on the parameters,such as M and C.Hence,according to the Hurwitz stability criterion,the stability criteria for the projectile with fixed canards shown in inequalities(11)are similar to those derived in Ref.[9].
Where p2= (H-2g*)2+P2- (2-2εαe)M/(1-2εαe)-2εβePT/(1-2εαe);=2T≈M/(1- εαe)+ εβePT/(1- εαe)2+εβePM/[(1- εαe)=(1- εαe)(H-2g*);=P2/(4).
3.Control strategy influence on stability
Since the wingspan and deflection angle of canards are immutable,the rolling speed and roll angle of the forward body of this projectile are controlled by the motor torque exactly.Therefore,the control strategy of the dual-spin projectile with fixed canards means the motor torque during the control period in order to satisfy the requirements of guidance system.Neglecting the indirect effect of the motor torque on the Magnus force and Magnus moment,the changing of the motor torque only affects the rolling movement,which includes the rolling speed and roll angle of the forward and aft bodies pA,pF,γA,γF.
For the sake of simplicity,the study on the influence on stability of control strategy is divided into two steps:the analysis on the effects of the rolling movement on stability and the control strategy on rolling movement.The main problem in the first step is the influence law of the rolling movement on the stability parameters.The second step is to study the dependences of the rolling movement parameters corresponding to the results obtained in the first step on the control strategy.
3.1.Impact of rolling movement on stability
As is known to all,the stability margin indicates the distance between the operating point and the critical stable state.The infl uence of the control strategy on the stability is transformed into an optimization of the stability margin under different control strategies.Because of stability of this projectile is assessed through three parameters p1,p2and Cdynasynchronously,the influence on stability should take these three aspects into account comprehensively.
3.1.1.The first stability parameter p1
According to the aforementioned analysis,it is reasonable to assume that with the variation of control strategy-the motor torque,only the rolling movement-pA,pF,γA,γFvaries,other than the other trajectory characteristics such as velocity,the pitch angle et al.Therefore,the parameters unrelated to rolling movement such as g*,H,M,,areindependent fromthecontrolstrategy.Consideringthe definition p1=2(H-2g*),the first stability parameter p1is invariant with the rolling movement as well as the control strategy.
3.1.2.The second stability parameter p2
In view of the definition of p2,the variation of this stability parameter under different pA,pF,γA,γFcan be expressed as
Since|PT|is usually much smaller than M[18],neglecting the variation ofβeunder different rolling movement and letting 1-2εαe≈1 and 1- εαe≈1,equation(12)can be calculated approximately as
To simplify the analysis,the rolling speeds corresponding to this stability characteristic p2to be compared are recorded as pA+ΔpA,pF+ΔpFand pA,pFrespectively.As the moment of inertial is the inherent property of the projectile,and the variation of velocity caused by different control strategies is small enough to be neglected,Δp2is a function that depends on pA,pF,ΔpFand ΔpA.Compared with pA-dependent term,it is reasonable to neglect the terms correlated to pF,ΔpF,ΔpAand the starred coefficients along with trim angle of sideslipβe,so thatΔp2shown in equation can be simplified and rewritten as
According to the stability criterion p2>0 and equation(14),the stabilitycorresponding to p2will ascend with the increasing ofΔp2,in other words,the stability corresponding to p2will increase when IxFΔpF+IxAΔpA>0;otherwise,the stability will weaken.
3.1.3.The third stability parameter Cdyna
According to dynamic stability condition shown as the third inequality of criterion(11),the dynamic stability is enhanced with increasing of Cdyna.Similarly to the analysis in the previous section,the rolling speeds corresponding to the dynamic criterion characteristic Cdynato be compared are recorded as pA+ΔpA,pF+ΔpFand pA,pFrespectively.Substituting the aforementioned definition ofandthe variation of Cdynaunder different rolling speeds of the forward and aft bodies can be expressed as
As the rolling speed of the aft body are much larger than that of the forward body and variations of these rolling speed caused by control,Δλ,ΔΦ and ΔΦ2can be calculated and simplified as
Substituting equations(16)and(17)into equation(15),the dynamic criterion characteristic neglecting the small values can be rewritten as
3.2.Influence of control strategy on stability
According to the aforementioned analyses of the influence of control strategy on the flight stability,the variation of the flight stability is characterized by
whereΔCp2represents the influence on the stability corresponding to the second criterion;ΔCdynarepresents the influence on that corresponding to the third one.
As is known to all,the stability margin indicates the distance between the operating point and the critical stable state.It can be seen from equations(14)and(19)that the change of stability margin corresponding to p2equals toΔCp2,and the change of dynamic stability margin equals toΔCdyna.So the larger these characteristics are,the more stable the projectile is.
To assess the influence on stability synthetically,a function(shown in equation(21))colligates the relative variation of the second and the third criterion of formula is defined.As the parameters in this function are dynamic,it is a function of time under a specific control strategy.
where p2and Cdynaare the stability parameters corresponding to the free flight ballistics at the time to study.
For sake of simplicity,the motor torque is divided into two parts:the balancing torque moment of the forward body MmoSand the rest momentΔMmowhich is related to the control strategy directly.
Substituting Mmo=MmoS+ΔMmointo equation(6),it can be obtained that during roll angle keeping period,the variation rate of the rolling speed of the aft body can be calculated by
Assumingthesamecontrolstrategyisimplementedwhichmeans ΔMmoisthesame,theevaluationparametershowninequation(21)is proportional toΔpAwhose coefficient is usually positive because of the stability of the free flight projectile should be guaranteed.Therefore the flight stability will increase with the increasing of pA.Although MrdAis proportional to pA,the major factor of˙pAis the driving moments instead of the retardation torque MrdA,which means˙pAwill decrease with increasing Mrc.In conclusion,the flight stabilityof thisprojectileisstrengtheningwithdecreasingMrc,under a determined control strategy.To evade or decrease instability risk of the projectile with fixed canards,a pair of spin canards whose roll moment is as small as possible should be designed.
When the structure of projectile is determined,a variable motor torque characterized byΔMmois executed to complete the instructions issued by guidance system.It can be seen from equation(22)that the rolling speed of the aft and forward bodyare governed byΔMmo,as well as by the roll damping moments which interact with the rolling speeds.To predigest the calculation ofΔpF,ΔpAcaused byΔMmo,an iteration method whose derivation process is shown in Fig.3 is proposed by means of considering the change of rolling speeds as a gradual process.According to the iteration flow shown in Fig.3,ΔpF,ΔpAcan be expressed as
where In(*)represents the n-ple time integral of*.Due to the roll angle variation is the time integral of the corresponding rolling speed variation,ΔγF,ΔγAcan be expressed as
To analyze the impact of control strategy namelyΔMmoon theflight stability,substituting equation(25)into equation(20),the
characteristics representing the variation of stability can be rewritten as
Substituting equations(25)and(26)into equation(21),the criterion for assessing the influence on flight stability of control strategy can be rewritten as
To avoid inconsistencyand the potential possibility of resonance[19]caused by the free rotation of the forward body,it is necessary to hold pFto a specific value rather than non-control when the uncontrolled instruction is issued.Based on the control characters,the control period is divided into four parts(shown in Fig.4):the roll speed controlling,the roll speed keeping,the roll angle switching and the roll angle keeping period.In the roll speed controlling period,pFis controlled from one value to another;analogously,γFis switched from one value to anther in the roll angle switching period.In the roll angle/speed period,γFor pFremains as a designated value.
After the projectile passes muzzle,a short period of free flight are take place for the initialization of the missile-borne circuit system.Once a signal has been received to start,the rolling speed of the forward body is controlled from a negative value to zero or a specific value in the roll speed controlling period subsequently.And then an adjustment to the roll speed or angle of the forward body required by the guidance system is made.When the guidance system commands stopping control,the control mode is switched into the roll speed controlling period followed by a roll speed keep period.These control periods can switch to each other during theflight process under the command from guidance system.
3.2.1.Roll speed controlling period
As is commanded by the guidance system,the starting and stopping time and the variation of the forward body's rotation speed of this period are immutable.The difference between the forward body's rotation speeds at the starting and ending point is recorded asΔpFv,and the control time during this period is tv.
As the stability characteristic shown as equation(27)is variable with the time,it is one-sided to assess the stability at any moment of a period.To assess the stability of this period overall,the stability assessment during a period to be studied should be judged by the integration of G(t),which is recorded as Sp
Where tbis the beginning time of the period to be studied,and teis the ending time of this period.
For the sake of simplicity,ΔMmois considered as a superposition of the average and vibration ofΔMmo,which can be recorded as
WhereΔMmoarepresents the average ofΔMmo,andΔMmovrepresents the vibration during the study period.
Considering the definition ofΔMmovand ΔMmoa,the single and double integral ofΔMmocan be expressed as
Substituting equation(30)into equation(25)and equation(28),it can be obtained that
Dividing the control time into n segments,the integrations can be turned into the sums of these segments:
Where h= (te-tb)/n=tv/n;n is infinity;ΔMmov(i)is the ΔMmovin the i segment.Hence equation(31)can be rewritten as
As tvandΔpFvare invariable,the stability ascends with the increasing of the second item.According to equation(33),Sphas a maximum value when ΔMmovfollowing the change of(n-i+1)(K3+K4h(n-i+2)/2).Considering the control time of this period is quite short,K3and K4may be taken as constants which can be calculated before this period.Consequently,though the analysis of (n-i+1)(K3+K4h(n-i+2)/2),the recommend change law ofΔMmovfor stability during the roll speed controlling period can be summarized as follows.
Through the deep analysis of the aforementioned preliminaryfindings,a broad regulation of general application is concluded that ΔMmoshould increase when K3-K4(t-tb-tv)<0 and decrease when K3-K4(t-tb-tv)>0 during the roll speed controlling period for the sake of stability.
3.2.2.Roll angle/speed keeping period
During the roll angle or roll speed keeping period,the roll speed of the forward body is held as a designated constant recorded as pFK,which can be described by the equation=0.Substituting into the firstequation of equation(6),it can be obtained that Mmo=MmoS=Mrc-Mrb-MrdFandΔMmo=0 during these periods.In other words,the control strategiesof these periodsaretheoretically definite when pFis immutable.
SubstitutingΔMmo=0 into equation(22),the rotational dynamic equations on the rolling direction can be written as
Because of the roll damping moment of the aft body is the secondary factor in the first equation which cannot change the variation trend ofand CrdFis negative,will decrease with increasing pFKwhen the roll moment due to spin canards is certain.Combining with the expression of the evaluation parameter shown in equation(21),a lower pFKshould be chosen on practical basis,in the interest of enhancing the projectile stability during the roll speed keeping period.
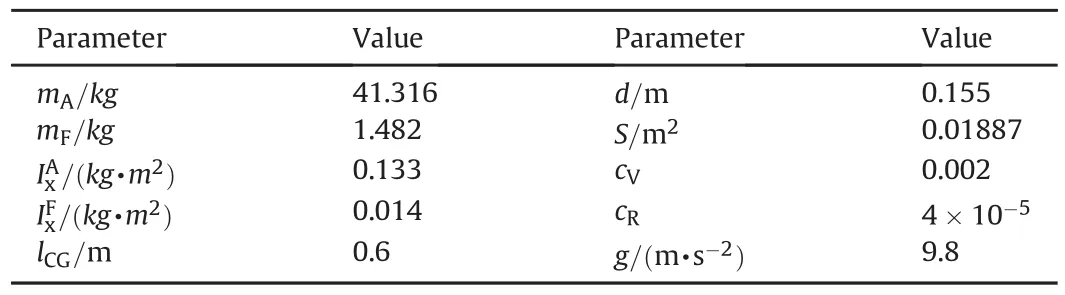
Table 1 Physical properties for 155 mm dual-spin projectile.
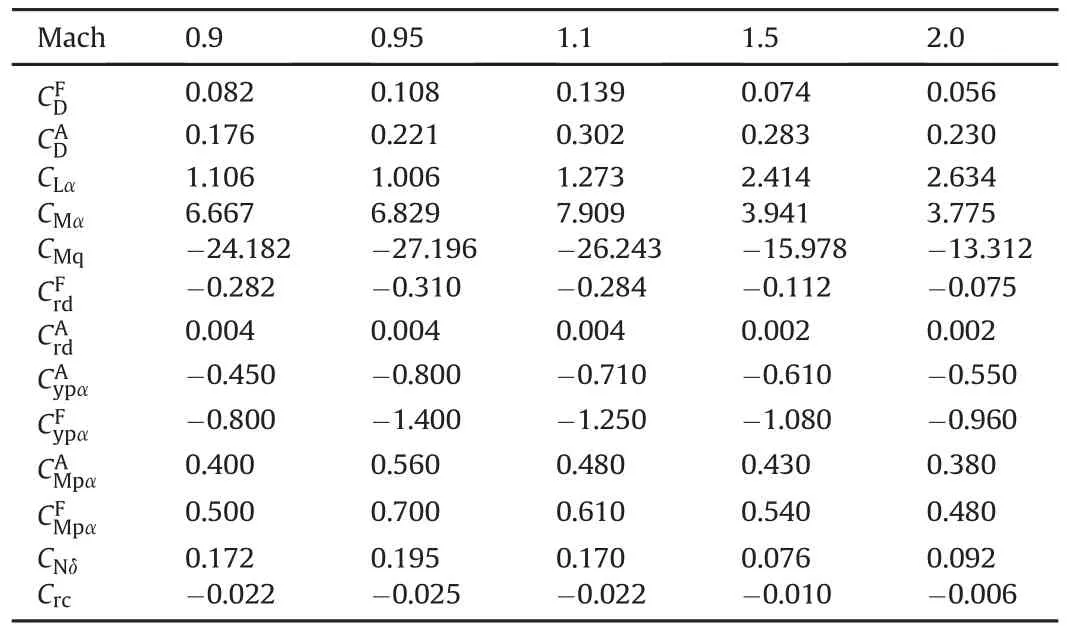
Table 2 Aerodynamic coefficients for 155 mm dual-spin projectile.
3.2.3.Roll angle switching period
At the starting and ending point of the roll angle switching period,the variation of rotation speeds of the forward body during this period ΔpFASis a specific value.AsγFat the beginning and ending of roll angle switching period(recorded asγFASBand γFASErespectively)are commanded by the guidance system,considering the operational principle of the actuator of the dual-spin projectile with fixed canards,the variation ofγFduring this period should satisfy the equation ΔγFAS= γFASE-γFASB+2Kπ,where K can be any integer.
Similarly to the analytical method used in the roll speed controlling period,ΔMmois decomposed into the average valueΔMmoaand the vibrationΔMmov,so thatΔpFASandΔγFAScan be expressed as
where tsmeans the control time of the roll angle switching period.For the sake of the requirements of guidance system,the control time of this period is quite short compared to that of roll angle keeping period followed with it.As is analyzed above,the stability is independenton the control strategy during the rollangle keeping period,so that the stability at the ending point should be studied instead of that during the roll angle switching period.
Substituting equation(35)into equation(27),the stability at the ending point of this period can be expressed as

Table 3 Spand convergence rate with differentΔMmo(tv=1s).
From equation(36),several results can be obtained that.
(1)The stability of projectile is irrelevant to the control strategy ofΔMmoduring the roll angle switching period when ΔγFASis definite;
(2)when K4>0,the larger K is,the more stable the projectile is;when K4<0,on the contrary.
4.Simulations
To verify the influence of control strategies on the flight stability deduced above,nonlinear trajectory simulations are run for 155 mm dual-spin projectile with fixed canards.All simulations results are obtained from a fixed-step(0.005s),forth-order Runge-Kutta numerical integration of the 7DOF equations of motion.The shells are launched from 0 m under the initial conditions of V=630m·s-1,θ=45°and pA=1277rad·s-1.The physical properties and the aerodynamic coefficients for the 155 mm dual-spin projectile are listed in Table 1 and Table 2 respectively.
4.1.Roll speed controlling period
In these 7DOF simulations,the roll speed controlling period which starts at 20s,under different control strategies is followed with the same free ballistic flight.In order to avoid the influence of the subsequent control state,pFafter the roll speed controlling period is kept as 5 rounds per second(r·s-1).The parameters K3,K4at 20s of the trajectory are 0.0311 and-0.0442 respectively,so K3/K4during this period can be estimated as-0.704.According to the theoretical analysis above,when tv=1s,the motor torque first ascending and then descending taken the turning point as 20.3s is recommend;when tv=0.5s,the monotone increasing one is.
When control time tv=1s,in order to investigate the stability of projectile under different motor torques,a set ofΔMmoshown in Fig.6 are applied at the projectile under the same initial conditions before the roll speed controlling period.The angular motions of the 155 mm projectile during 20-25s under different control strategies are shown in Fig.7.
As the result of stability comparison under different control strategies during this period is variable,it is unjustified to compare the angular motion at any time of this period.Considering the subsequent roll speed keeping periods of these trajectories are at the same pF(5r·s-1),whose influence to stability is the same,it is reasonable to compare the stability under different control strategies of the roll speed controlling period based on the convergence rate of angular motion during the roll speed keeping period.The theoretical approximate calculated values of Spwith different ΔMmo(shown in Fig.6)and the average of convergence rate ofα andβduring the roll speed keeping period obtained by simulations are shown in Table 3.
Table 3 and Fig.6 shows that the trajectorycorresponding to the larger theoretical stability assessment characteristic Sphas larger convergence rate during the roll speed keeping period,and the largest Spand convergence rate are obtained under A1#ΔMmowhich is increasing before 20.3s and decreasing after that.
Similarly to the simulations above,when the control time of roll speed controlling period is set as 0.5s,the angular motions of the 155 mm projectile during 20-25s under different control strategies in Fig.8 are shown in Fig.7,and the corresponding Spand convergence rate of angular motion are listed in Table 4.
Figs.8 and 9 and Table 4 demonstrate that the change trend of the convergence rate and Spunder differentΔMmoare the same,and the largest one is obtained under B3#,which is monotonously decreasing.
To conclude,these simulation results of different tv(0.5s or 1s)are in line with the theoretical analysis.
4.2.Roll speed keeping period
To verify the theoretical analysis results of the roll speed keeping period,7DOF simulations are run under the same initial conditions with different roll speed of the forward body(-10r·s-1,-5r·s-1,5r·s-1and 10r·s-1).In order to avoid interfering by the other control periods,only the roll speed keeping period is taken place in these simulations.
The angle of attack of these simulations and the zoom view of it are shown in Fig.10 and Fig.11 respectively.Fig.10 shows that the angle of attack shots up at 40s when pF=10r·s-1;shots up at 45s when pF=5r·s-1;changes smoothly when pF=-5r·s-1or-10r·s-1.In other words,the whole trajectory is stable when pF=-5r·s-1or-10r·s-1;unstable at 45s when pF=5r·s-1and at 40s when pF=10r·s-1.It is observed from Fig.11 that greater pFis relatively to larger magnitude of angle of attack during this period under the same initial conditions.These simulation results show that the flight stability decreases with the increasing of pF,which is consistent with the theoretical results.
4.3.Roll angle switching period
The simulations of the influence of co ntrol strategy during roll angle switching period on stability of the projectile are divided into two parts:the sameΔγFand differentΔγF.
In the simulations of the same ΔγF,the roll angle switching period begins at 21s,and the γFis switching from 180°to 270°.The initial conditions and control strategies during the flights other than the roll angle switching period are the same.The angular motions of the projectile during 21-25s under different control strategies(shown in Fig.12)are shown in Fig.13.
Figs.12 to 13 demonstrate that pAafter the roll angle switching period under different control strategies are nearly the same;the angular motions under different control strategies are similar numerically.These phenomena conform to the stability analysis during the roll angle switching period when ΔγFis the same.
Simulations are running with ΔγF=0.5π+2Kπ(K=0,±1)and the same control time of this period 1.5s.The initial conditions and parameters of these simulations are the same with the previous simulations.The angular motion with different K value during 21-25s is shown in Fig.14.
Fig.14 demonstrates that the angle of attack is increasing with K,especially the angular motion goes unstable when K=1.In sum,to satisfy the same command from guidance system,the projectile's stability descends with the increasingΔγF.Since K4at this time is approximately equal to-0.046 which is negative,the phenomena in the aforementioned simulations conform to the theoretical predictions very well.
5.Conclusion
The influence of control strategy is investigated on the stability of the dual-spin projectile with fixed canards in this effort.Using the projectile linear theory and the Hurwitz stability criterion,the linearized angular motion and the stability criterions have been formulated.To study the influence of the control strategy on stability,a parameter for assessing the impact is defined through comprehensive consideration of the stability criterions.For the sake of the difference between the control features,the controllingflight is separated into three periods,and the influence of control strategy is studied in these parts separately.
Based on the theoretical analysis,the following conclusions can be obtained.To evade or decrease instability risk of the projectile with fixed canards.
(1)A pair of spin canards whose roll moment is as small as possible should be designed;
(2)A lower pFKshould be chosen on practical basis during the roll speed keeping period;
(3)During the roll speed controlling period:ΔMmoshould increase when K3-K4(t-tb-tv)<0 and decrease when K3-K4(t-tb-tv)>0;
(4)During the roll angle switching period:when is definite,the stability of projectile is irrelevant to the control strategy of ΔMmoduring the roll angle switching period;when K4>0,the largerΔγFASis,the more stable the projectile is,vice versa.
Numerical simulations of 155 mm dual-spin projectiles indicate that the influence of control strategies on the stability gives satisfactory agreement with numerical results.
- Defence Technology的其它文章
- Novel approach to quantify the chemical stability and shelf life of modified double-base propellants
- Study on buffering performance of thin-walled metal tube with different angles
- Path planning in uncertain environment by using firefly algorithm
- An experimental and numerical approach-characterisation of power cartridge for water-jet application
- Analysis and use of fuzzy intelligent technique for navigation of humanoid robot in obstacle prone zone
- The law of barrel wear and its application

