Understanding the mechanisms of friction stir welding based on computer simulation using particles

A.Yu.Smolin,E.V.Shilko,S.V.Astfurov,E.A.Kolubev,G.M.Eremin,S.G.Pskhie,c

aInstitute of Strength Physics and Materials Science SB RAS,Tomsk,634055,Russia

bTomsk State University,Tomsk,634050,Russia

cSkolkovo Institute of Science and Technology,Skolkovo,143025,Russia

Keywords:Friction stir welding Plastic flow Deformation mechanisms Simulation Particle method

A B S T R A C T Friction stir welding(FSW)is a novel technique for joining different materials without melting.In FSW the welded components are joined by stirring the plasticized material of the welded edges with a special rotating pin plunged into the material and moving along the joint line.From the scientific point of view,the key role of the FSW processes belongs to formation of the special plasticized conditions and activation of physical mechanisms of mixing the materials in such conditions to produce the strong homogeneous weld.But it is still a lack of complete understanding of what are these conditions and mechanisms.This paper is devoted to understanding the mechanisms of material mixing in conditions of FSW based on a computer simulation using particles.The movable cellular automaton method(MCA),which is a representative of the particle methods in mechanics of materials,was used to perform all computations.Usually,material flow including material stirring in FSW is simulated using computational fluid mechanics or smoothed particle hydrodynamics,which assume that the material is a continuum and does not take into account the material structure.MCA considers a material as an ensemble of bonded particles.Breaking of inter-particle bonds and formation of new bonds enables simulation of crack nucleation and healing,as well as mass mixing and micro-welding.The paper consists of two main parts.In the first part,the simulations in 2D statements are performed to study the dynamics of friction stir welding of duralumin plates and influence of different welding regimes on the features of the material stirring and temperature distribution in the forming welded joints.It is shown that the ratio of the rotational speed to the advancing velocity of the tool has a dramatic effect on the joint quality.A suitable choice of these parameters combined with additional ultrasonic impact could considerably reduce the number of pores and microcracks in the weld without significant overheating of the welded materials.The second part of the paper considers simulation in the 3D statement.These simulations showed that using tool pins of different shape like a cylinder,cone,or pyramid without a shoulder results in negligible motion of the plasticized material in the direction of workpiece thickness.However,the optimal ratio of the advancing velocity to the rotational speed allows transporting of the stirred material around the tool pin several times and hence producing the joint of good quality.

1.Introduction

One of the most outstanding achievements of the last decades in the field of production of non-detachable joints is the development of the technology of friction stir welding(FSW)[1].This technique was patented at the end of 1991 by The Welding Institute UK and found wide application in space and aircraft industry in the middle of the 1990s[2-5].Recent studies have shown that FSW is a very effective way to obtain high-quality joints for structures of various dimensions and shapes,including sheets,3D profile structures,and pipes.The main feature of the FSW is the ability to weld the joined materials without melting.The consequence of this is the great number of advantages of FSW in comparison with conventional welding methods like electric arc welding,electron beam,and laser welding.Among these advantages are the absence of hot cracks,melt,and defects caused by solidification of the liquid metal,changes in material properties due to its significant superheating,possibility to join dissimilar alloys and materials(including those that were earlier considered to be impossible to weld by traditional welding methods)[4-6].More of that,based on the principles of FSW a special surface processing technique(so-called friction stir processing)has been developed and utilized to modify and strengthen the surface of different materials[7-9].

The main problem in the industrial application of FSW technology is associated with the correct choice of technological parameters of the process,such as the tool shape[10-12],penetration depth,rotational speed and longitudinal velocity of the pin,etc.[4-6].A non-optimal choice of the FSW regimes often reduces the weld quality due to the formation of a large number of differentscale defects in the weld.However,it is unfeasible to define the optimal regime and parameters without a deep insight into the fundamental processes taking place in the material during FSW.Since the early 90s,a lot of experimental and simulation studies of FSW have been performed in order to understand the peculiarities of material flow,heat generation and temperature distribution,material microstructure changes,etc.[3-14].Unfortunately,the main fundamental problem of FSW,which is the understanding the mechanisms of severe plastic deformation that enable plastic flow,stirand material coalescing behind the rotating and moving pin(i.e.plasticized material behavior in FSW)still remains unclear.

Most of the simulations of FSW are performed using the finite element method[14].Because the joining materials experience severe plastic flow and stir while the tool is almost rigid,materialflow in FSW is usually simulated based on computational fluid mechanics.To take into account the pin deformation and heating the so-called Arbitrary Lagrangian Eulerian Approach is the most suitable for solving such problems[14,15].All these methods belong to the continuum concept in mechanics,i.e.they assume that the state controlling variables distribute in space continuously and does account for the material structure.At the same time for describing severe distortion and failure of a material in Lagrangian approach,the most promising are so-called meshless(or meshfree) methods,namely smoothed particle hydrodynamics[16-19].To be precise,meshless methods are not pure particle ones.They just use scattered nodes to discretize continuum mechanics equations in space,i.e.they are really based on continuum approach.The principal difference of particle methods from computational methods in continuum mechanics is the replacement of continuous representation of a material by an ensemble of interacting particles.This,in turn,determines the difference in governing equations as well.Thus,partial differential equations of continuum mechanics are replaced by Newton-Euler equations governing the motion of a particles ensemble.Constitutive laws for the considered material in tensor form(which conventionally describe relationships between local stresses and strains or their time derivatives)therewith are replaced by potentials/forces of inter-particle interaction.One of the most important features of particle-based methods is an inherent capability of particles to change their surroundings,i.e.interacting neighbors.This makes discrete element methods[20-22]very attractive for direct simulationof complicated processes of severedeformation including stir taking place in FSW[23,24].

The key point,which determines the mechanical behavior of a discrete elements ensemble,is the structural form of the expressions for interaction forces between elements and the relationship between these expressions and the constitutive law of the modeled material.Usually,pair-wise elastic interaction forces,which can be treated as springs between elements,are used.The spring stiffness is derived on the assumption that strain energy stored in a unit cell of deformed element ensemble is equal to associated strain energy of the equivalently deformed continuum[21,22].However,an approximation of pair-wise interaction has a number of important limitations,in particular,fundamental problems in the correct simulation of irreversible strain accumulation in ductile materials[25,26].

Previously,we showed that these problems can be solved by using many-particle interaction [25,26].Such formulation is adopted from the Wiener-Rosenblueth model of cellular automata[27,28]and this hybrid technique is referred to as the movable cellular automaton method[29,30]usually abbreviated as MCA.The main advantage of the generalized expression for interacting forces is the ability of trivial establishing the relationship between vector parameters of the inter-particle interaction and tensor parameters of the material constitutive law.As a result,we can adopt different models and criteria of elasticity,plasticity,and fracture to the formalism of MCA.

This paper is devoted to the theoretical investigation of the peculiarities of material deformation,flow,and stir,as well as heat generation taking place in FSW in order to understand the basic mechanisms of these processes.The investigation was based on computer simulation by the MCA method,which considers a material as an ensemble of bonded particles and allows accounting for the material structure.The breaking of inter-particle bonds and formation of new bonds enables simulation of crack nucleation and healing,as well as material stir and microwelding.

2.Method of movable cellular automata

It is assumed that a material under consideration consists of elementary objects of finite size(automata)which interact among each other and can rotate and move in space,thereby simulating a deformation process of the material.The motion of such automata is governed by the Newton-Euler equations

It has to be noted,that automata of the pair may represent the parts of different bodies(contacted pair)or of one body(bonded pair,its interaction really is not a contact one).That is why further we will put the word “contact”in quotation marks.The automaton size is characterized by one parameter di,but it does not mean that the shape of the automaton is a sphere in 3D or a circle in 2D.Real shape of the automaton is determined by its “contacts”with neighbors.

For isotropic material the volume-dependent part of the total force can be written as follows[25,26]where Pjis the pressure in the volume of the neighboring automaton j,Sijis the area of interaction surface of automata i and j and A is defined by the ratio of elastic properties of the material.

Let us rewrite the total force acting on automaton i as a sum of normalandtangentialcomponents

To compute components of the average stress tensor in the bulk of automaton i we can use homogenization procedure described in Refs.[25,26]

whereαandβdenote the global coordinate axes X,Y,Z,Viis the automaton volume,nij，αis theα-component of the unit vectorand Fij，βis β-component of the total force acting at the point of“contact”between automata i and j.The pressure Pi(or the mean stress)in the bulk of automaton can be computed from thus defined stress tensor

We can also compute the other tensor invariants in the bulk of automaton,in particular,von Mises stress

From Equations(1)-(3)itfollows that thespecific expressions for computingandactually determine the rheology of a model material.

For further convenience,the central and tangential interaction of the automata i and j are characterized by the corresponding stressesηijand

Because this study uses the two-dimensional as well as threedimensional simulations,the shear stressin(6)is a vector in the plane which is normal to

Deformation of automaton i under its normal interaction with automaton j is characterized by the normal strain

Because each automaton of a pair may represent different material,the pair overlap is somehow distributed between both ith and jth automata

where Δ denotes an increment per integration time stepΔt.The strain distribution rule in the pair is defined by the expression for computing interaction forces.For central interaction it is similar to Hooke's law for diagonal components of stress tensor

where K and G are the bulk and shear moduli of ith automaton material,the pressure Pimay be computed using(3)and(4)at previous time step or by a predictor-corrector scheme.

The starting point to characterize shear deformation in automata pair is a kinematics formula for free motion of a rigid body applied to the pair i-j

Along with this pair rotation each automaton rotates with its own rotational velocity(Fig.2).Hence the increment of shear strains of both automata i and j per time stepΔt is defined by the relative tangential displacement at the contact pointdivided by the distance between the automata

The increment of tangential force can be expressed similarly to Hooke's law for non-diagonal stress tensor components

The difference in rotations ofthe pair automata causes deformation of relative “bending”and “torsion”of the pair as well(Fig.3).The pair resists to such relative rotation via the torque,which value can be computed as follows

Formulae(1)-(14)describe the mechanical behavior of a linearly elastic body in the framework of the MCA method.To describe elastoplastic flow of the material,it was proposed to use the plasticflow theory(namely von Mises model)byadapting the algorithm of Wilkins in the MCA method[25,26].Radial return algorithm of Wilkins consists in the solution of the elastic problem in increments and subsequent“drop”of components of stress deviator tensor Dαβ= σαβ-1/3σkkδαβto von Mises yield surface in the case that equivalent stress exceeds it(Fig.4)

where M= σpl/σint,σintis the equivalent stress,σplis the current radius of von Mises yield circle.

Applied to the automaton i,this algorithm can be written as follows

where α,β denote global coordinates X,Y,Z and α≠β;andare returned components of the average stress tensor;andare the corresponding stress tensor components obtained from the solution of the elastic problem;Mi=is the current radius of von Mises yield circle.

The specific normal and tangential interaction forces are also corrected using the obtained value of coefficient M[25,26]

Thus,rheological properties of the automaton material are actually defined by the unified hardening curve）(hereis the equivalent strain that can be computed similarly to[25,26]);this dependence is referred to as the automaton response function.

The equations of motion(1)are usually integrated with the use of the velocity Verlet algorithm modified by introducing a predictor for estimation ofat the given time step[25].

A pair of automata can be in one of two states:bound and unbound.Thus,in MCA fracture and coupling of fragments(crack healing,microwelding etc)is simulated by the corresponding switching of the pair state(Fig.5(a)).Switching criteria depend on physical mechanisms of material behavior.Note,that knowing stress and strain tensor in the bulk of an automaton makes possible direct application of conventional fracture criteria written in tensor form.

To be precise,for use such a criterion we need to know local stress tensor at the area of interaction(“contact”)of the considered pair i-j(hereinafter we denote this tensor as).In the local coordinate system X′Y′of the pair defined in Fig.5(b)the componentsandare equal to the specific forces of central(σij)and tangential(τij)interaction of the pair.The other componentsandmay be defined by linear interpolation of the corresponding values in the centers of the automataand

where a= σc/σtis the ratio of compressive strength σcto tensile strength σtof the pair,andare the corresponding invariants of the stress tensor

Usually,we use an explicit scheme for integrating the motion equations.In this case,the value of time stepΔt is limited above by the time of sound propagation throughout the bulk of automaton.Practically the time step is equal to or less than a quarter of this limit.Therefore,bond breaking during one time step actually suggests that separation of automata materials takes place simultaneously over the whole area of the automata “contact”,which is not true.That is why herein we use a more accurate description of the crack growth.It is assumed that the breaking of a bond is a process distributed in time as well as space.For this purpose,we introduce the dimensionless factor(0≤≤1)which has the meaning of the portion of the bonded part of the contact area Sij.Thus,the dynamics of bond breaking is determined by the dependence（t）,wheredecreases from the initial value 1 to the final value 0.Depending on the internal structure of the material the crack growth may be stable or unstable,which can be described by two corresponding models for the dependence

In the case of stable crack growth(first model),the bond breaking is governed by the predefined functionwhereis the equivalent strain at the pair“contact”.In the simplest case,this function can be constant.

In the case of unstable crack growth(second model)it is assumed that if the fracture criterion threshold is exceeded then a bond breakage(crack)begins to grow in time t according to the specified lawIn the simplest case,this function can be constant as well,which means that the crack propagates throughout the pair “contact”area with the constant velocity Vcrack.

Unbonded(i.e.contacting)automata do not resist to tension,and their tangential force is limited by the dry friction model(for example,Amonton's law,Dieterich's model and so on).

To model a new bond formation in the pair of unbonded automata we use special criteria based on two threshold values.First is the magnitude of the central compression strength,it should be equal to yield strength,i.e.pair should experience plastic deformation.The second is the magnitude of plastic work(heat)in the pair,which means that to form a new pair of bonded automata the forces applied to the pair have to perform the work equal to the energy of the new chemical bond Wb.

3.Material characterization

Herein we model friction stir welding of two plates of aluminum-based alloy D16(duralumin).The input parameters of the model within the MCA method formalism are the elastic characteristics and the stress-strain curve for the uniaxial tension of the simulated material,which determine the response function of a movable cellular automaton.The elastic mechanical properties of the material werecharacterizedbythe following parameters:the shear modulus G=27.27GPa,the bulk modulus K=66.67 GPa.Plastic behavior was characterized by the yield stressσy=274 MPa and linear work hardening up to the strength limitσt=800MPaat the ultimate strain εt=0.15.Thus,the response function of the cellular automata simulating the welded plates was described by the elastic-plastic loading curve with linear hardening(Fig.6)plotted byapproximating the uniaxial tension curve of macroscopic duralumin samples.

An essential advantage of the MCA method,like a representative of discrete element methods,is that an element can change its neighborhood.This allows one to explicitly take into consideration the breaking and formation of bonds between material fragments simulated by individual elements.Bond breaking in the MCA method is simulated by switching the state of a pair of interacting discrete elements from so-called bonded to unbonded state.Pairs of unbonded automata can experience only contact interaction that includes the compression resistance force of a pair and dry/viscous friction force.The switching from bonded to unbonded state in this study was conducted using a Drucker-Prager fracture criterion(16)with ultimate tensile stressσt=800MPaand compression strength σc=700 MPa.The bond formation in pairs of unbonded(contacting)movable cellular automata was also simulated using a special criterion based on the value of plastic work in the pair to be equal to Wb=50 MJ/m3.

4.Results of 2D simulations

4.1.Geometry of the model and scheme of loading

A two-dimensional structural model used tostudy the dynamics of FSW within the MCA method framework is shown in Fig.7.The motion of an absolutely rigid disc(hereinafter referred to as a tool pin)rotating about its center and moving along the interface of two metalplateswasconsidered.The plate dimensionswere 10×25 mm.The diameter of the tool pin was 3 mm.The pin was initially placed at a distance of 8mm from the left lateral surface of the simulated system.This position of the pin was chosen to minimize the influence of the lateral faces(particularly,elastic wave reflection)on the dynamics of the FSW process.

A three-stage scheme of loading was used.On the first stage,the initial stress state of the system was simulated by its hydrostatic compression and pin rotation.This stage was necessary because we simulated a relativelysmall fragment of the joined materials.In this case,a large number of elastic waves can propagate in the joining plates as well as high elastic stresses can arise during the pin rotation.On the second stage,the lateral,upper and lower faces of the simulated system were fixed,and the systemwas kept until the force equilibrium was reached.On the third stage,the FSW process was simulated by the pin motion with translational velocity Vtransalong the joint line between the two plates and its rotation about the disc center with angular velocityω(the instantaneous linear velocity on the disc surface was Vrot=ωR,where R is the pin radius).In the framework of the considered model,the lateral,top and bottom surfaces of the modeled system were fixed(Fig.7).

4.2.Analysis of the different regimes on materials mixing

In this section,the dynamics of friction stir welding is analyzed.The computer simulation results have shown that when the rotating pin starts to rotate the materials of the plates adhere to the pin surface,fragments of materials in the contact region between the joined plates and the pin are torn off and intensively stirred(Fig.8(a)).As the pin advances,the materials of the plates continue to stir and the stirred material is transferred from the front(region to the right from the rotating pin in Fig.8)to the back side around the pin(Fig.8(b))toformtheweld(Fig.8(c)).It is seen fromFig.8(c)that the region behind the pin includes at least two zones.Directly behind the pin,an area is observed where the processes of mixing of the substance take place and which is characterized by relatively high porosity.At a distance of about 1/6 of the pin radius,we can see the area where the mixing process is completed.This zone is characterized by a relatively uniform distribution of the welded materials.The produced weld is slightly asymmetric relative to the joint line between the plates.The width of the weld zone below the joint line is by about 7%larger than that of the upper zone(Fig.8(c)).This result agrees well with the available experimental data[3-6].

Analysis of the computer simulation results showed that the weld quality,which is determined by its porosity,uniform volume distribution of welded materials,and other factors,greatly depends on the pin motion regime(on the ratio of the instantaneous linear velocity of rotation on the pin surface Vrotto translational velocity Vtrans).Therefore,a detailed study of the influence of this parameter on the formation of the weld was performed in the paper.For this purposes,the angular velocity of rotation of the pin was constant ω =1600π rad/s(Vrot≈7.6 м/с),and change in the ratio Vrot/Vtranscarried out by varying the welding speed Vtransfrom 0.05 to 1 m/s.Fig.9 and Table 1 illustrate the structure of the produced weld for three different pin motion regimes.It is seen from the figure that with decreasing value of Vrot/Vtrans(due to increasing velocity Vtrans)the weld quality decreases.For example,at Vrot/Vtrans=38(Vtrans=0.2 m/s,Fig.9(a))the weld joint has the ratherlow porosity(4.2 vol%,Table 1)and a small number of planar defects(microcracks).A doubled decrease in Vrot/Vtrans(Vtrans=0.4 m/s)leads to weld porosity increase more than 1.5 times(Table 1).In this case,the weld has a large number of long microcracks.With the further decrease in the ratio Vrot/Vtrans(Vtrans=0.84 m/s,Fig.9(b))the weld loses its continuity,there are macropores and macrocracks even at a large distance from the pin.The porosity value in the weld region amounts to 23.4vol%(Table 1).Consequently,the synchronization of the rotating and translational velocities of the pin is a necessary condition for producing welds with the low amount of pores,microcracks,and uniform volume distribution of the joining materials in the weld.

Fig.10 shows the plot of porosity of the forming weld versus the welding speed Vtrans.It is seen that this dependence has a pronounced two-stage character.At low welding speeds(Vtrans≤0.4 m/s)the presented dependence is nearly constant.In this interval,we also observe the formation of the welded joint with the minimum volume content of pores(less than 6vol.%,Fig.10).At the sametime,a significant increase in the welding speed(Vtrans＞0.4 m/s)leads to a significant increase in the porosity of the weld,and as a result a decrease of its strength characteristics.In this case,the motion of the rotating pin leads to the significant crushing of the material in the front area(in the direction of the pin motion).It should be noted that the lowest porosity(less than 5%)is achieved at the minimum welding speed(Vtrans≤0.2 m/s,Fig.10),which is not beneficial from the viewpoint of the technological process.

Table 1 Weld porosity versus pin motion regime.

Analysis of the simulation results shows that this kind of plot of the porosity versus the welding speed is greatly determined by the mass transfer characteristics.Fig.11(a)shows the histograms of distribution of the number of movable cellular automata(particles)according to their integral displacement in the process of welded joint formation for fourdifferent welding speeds Vtrans(the abscissa indicates the integral displacement of the particles d),normalized to the circumferential length the tool pin(Ltool).This parameter directly reflects the value of the mass transfer.Thus,the greater the number of particles that pass the longer path(integral displacement)the greater the mass transfer characterizes the FSW process for the given technological parameters.It should be noted that in the analysis of mass transfer only discrete elements,which is characterized by significant integral displacements(over 15%of the circumference length of the rotating pin),were taken into account.This is due to the fact that exactly these particles are directly involved in the process of mass transfer.

Analysis of the presented distributions for different welding speeds showed that increase in Vtransleads to an increase of mass transfer during the motion of the rotating pin.Thus increase of the welding speed up to 0.4m/s results in an increase of the number of particles,which are involved in an intensive mass transfer,from about 2.5%(at Vtrans=0.05m/s)up to～ 75%(～30 times,Fig.11(b)).Note,here it is considered that the particles are involved in an intensivemass transferif theirintegral displacement is greaterthan at least half of the circumference length of the tool pin(d/Ltool≥0.5).The significant increase in mass transfer with an increase in welding speed allows forming a quality weld with a low content of pores and defects(Fig.10).Further increase in Vtrans(more than 0.4m/s)leads to ceasing the increase of the number of particles participating in intensive mass transfer(Fig.11(b))and even to its reduction(down to 56%at Vtrans=1m/s).This means that the mass of the material,which is carried by the rotating pin during the welding process,becomes insufficient for formation of the qualitative welded joint.The result is a significant increase in the porosity of the weld at Vtrans＞0.4 m/s(Fig.10).A possible way to increase the mass transfer in this case(at high welding speeds)may be increasing of frequency of rotation of the pin(a greater increase in the ratio Vrot/Vtrans).However,in real systems,this can result in a substantial increase in the temperature in the welding area,fast wear of the rotating pin,formation of burrs,etc.[3,5].

Fig.12 shows the temperature fields in the forming welded joints for different welding speeds Vtrans.It can be seen that the increase in the welding speed leads to a significant increase in the temperature of the stirred material.The local temperature may reach 550°C in the front region(in Fig.12 on the right side of the rotating pin).Furthermore,the increase of the welding speed leads to an inhomogeneity of the temperature field in the forming weld.

Note that in the considered model the heat source is the plastic work.Thus,in the process of plastic deformation of the material,there is a dissipation of mechanical energy.In the framework of the used approach,it is assumed that all the dissipated energy is converted into heat and we did not account for the heat transfer.The analysis of the von Mises strain fields in the welding region at different welding speeds showedthatwith increasingofVtransmore intensive plastic deformation of the material takes place,especially in the front region of the advanced side(Fig.13).As a consequence,we can observe a temperature increase in the region of the rotating pin at high values of the welding speed.

4.3.Influence of the ultrasonic action on materials mixing

A possible way to improve the weld quality during friction stir welding is the application of additional ultrasonic vibrations to the pin during the joining process.Analysis of the literature[32,33]shows that such additional action can increase the fatigue strength of the welded joint,provides microcrack and pore healing,and increases the weld microhardness.In this paper,we theoretically studied the influence of vibrational action on the material mixing and the welded joint properties.Ultrasonic vibrationwas simulated byapplying to the pin additional sign-alternating velocity Vusalong the weld direction,which is characterized by amplitude Ausand frequencyνusin the ultrasound range

Different values of the amplitude and frequency of this ultrasonic action were considered.Below we will also characterize the power of the ultrasonic action by maximal displacement of the pin per one period of vibration Dus.

Analysis of the obtained results revealed that the application of an additional ultrasonic vibration to the rotating pin manifests itself mainly for low welding speed Vtrans.First,it reduces the porosity of the produced weld.For all the considered vibration amplitudes and frequencies,the weld porosity is lower than in the case of welding without ultrasonic treatment(comparison data are given in Table 2).The lowest weld porosity value(1.2 vol%)was obtained at Aus=6.28m/s andνus=33kHz.

Analysis of the total displacementof the automata in the process of FSW showed that the applied ultrasonic vibration does not change the distribution shown in Fig.11 dramatically even for thelow values of the welding speed Vtrans.Nevertheless,the temperature fields shown in Fig.14 allow us to conclude that an increase in the power of the ultrasound action cause increasing of the maximum temperatureof the material near the pin and its location.Thismeansthatadditionalultrasound vibration resultsin increasing of plastic work especially at the moments when the direction of the ultrasound vibration concurs with the translational speed of the pin.

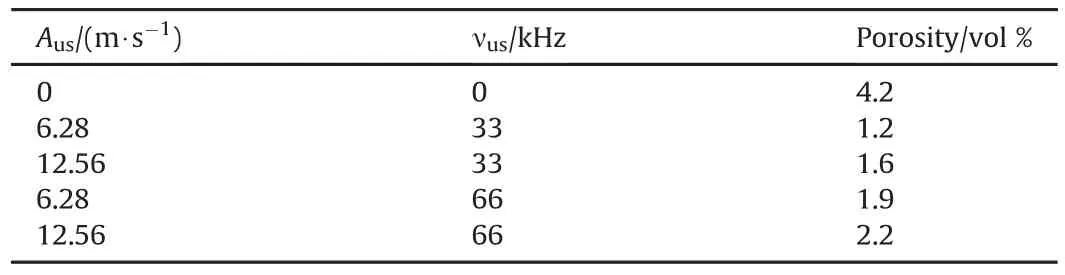
Table 2 Weld porosity versus ultrasonic vibration amplitude and frequency(Vrot=7.6 m/s and Vtrans=0.2m/s).

Increase in the frequency of the ultrasound vibration leads to more uniform temperature field and little decrease in its total value(Fig.14).Thus,high-frequency vibration acts like a peculiar“deformation pump”that uniformly redistributes stresses and plastic strains in the bulk of the material.This may be confirmed by pictures of the von Mises stress fields shown in Fig.15.One can see that increase in ultrasound frequency at the same amplitude decreases the high-stress volume in the material,which is characterized by active deformation(Fig.16)especially in front of the moving pin.At the same frequency,increase in the amplitude of the ultrasonic action leads to increasing of the total stress level in the joined materials(Fig.15)and,as a consequence,increasing the temperature around the pin(Fig.14).

5.Results of 3D simulations

5.1.Geometry of the 3D model and scheme of loading

Fig.17 depicts the model geometry,which was used in the 3D simulation herein.There were two plates of the in-plane dimensions of 6.5×18.0 mm(the dimensions were changed,with taking into account the 2D results obtained)and the thickness of 2.5mm.Joining of the plates was performed by rotating and moving of the hard pin(a cone in Fig.17)along the axis Y in its positive direction.The pin rotated with the speedωaround its axis,which was always parallel to coordinate axis Z.The initial position of the tool pin was located at the distance of 6mm from the left back face in Fig.17.

The pin motion started by only rotation with the speedω=800 1/s at the initial place.This preliminary stage was used to form a plasticized zone around the pin and took up to five full revolutions.Then the axis of the pin started to move along the joint direction with the constant velocity Vtrans.

To simplify our computation,the following boundary conditions were set.To simulate the restricting action from the supporting plate and the pin shoulder the automata were not allowed to cross the lower and upper surfaces of the geometry.We should note,that using such simplification resulted in neglecting of the rotation of the pin shoulder and getting the plasticized zone size much smaller than one in the real process.The automata at the other lateral surfaces of the plates were fixed.

The spatial structure of the automata in the weld region differed from the initial periodic packing.The number of the bonded neighbors of the automata in this region is not equal to the initial value of 12,which is the coordination number for fcc packing used in the simulation.It may be greater as well as less than this number.But the averagenumberof the bonded neighbors in the weld region is always less than 12.The less is this number the weaker is the weld material.Thus,to characterize the quality of the 3D model weld we proposed to use the plot of the number of bonded automata Nlin the simulated systemversus length of the pinpath S.Fig.18 depicts several typical curves of Nl(S).In the beginning,a strong decrease of Nlcorresponds to the initial stage of the loading when the pin just rotates and then starts to move.The main part of the plot,which is usually characterized by the constant linear decrease of Nl,corresponds to stable weld formation and indicates a good quality of the weld.

5.2.3D simulation results

First,we consider the influence of the welding speed Vtranson the dynamics of FSW process,which will be characterized by the plot Nl(S).In these computations,the rotational speed of the pin was the same and equal toω=800 1/s,and we varied only the welding speed from 0.05 up to 0.50m/s.The resulting plots for the number of bonded automata in the system versus the length of the pin path are shown in Fig.18.One can see that the optimal value of Vtransis equal to 0.10 m/s when automata of the plasticized material is transporting around the pin several times.The corresponding weld region are characterized by the minimum number of unbounded automata and their homogeneous spatial distribution.In the case of the welding speed of 0.50 m/s,we got the worst weld,and the program was aborted by reaching the critical inhomogeneity level of the weld.The results in Fig.18 also show that using the very slow welding speed results in the larger number of defects in the weld.These results are in very good agreement with the results of the 2D simulations presented above as well as the experimental evidence[2].

One of the advantages of 3D simulations is that herewe can vary the shape of the pin.To study the influence of the pin shape on the FSW process we created several different pins.The most interesting of them are shown in Fig.19(a)and may be grouped by their original geometrical bodies:cone,cylinder,and pyramid.The conical and cylindrical pins were also supplied by additional“wings”in order to enforce material to flow in the direction of the plate thickness.

The resulting plots Nl(S)for all these pins are shown in Fig.19(b).As one can see,the initial decay in the number of bonded automata is proportional to the surface area of the pin.However,as it was mentioned before,the quality of the weld is determined by the inclination and smoothness of the main part of the plot Nl(S).This fact allows us to conclude from the presented results that the best pin shapes in terms of the weld quality(minimum number of defects)are 2,3,6(Fig.19(a)).From the point of view of the process stability,only shapes 1,6,and 7 allowed us to get the homogeneous weld.

Fig.20(d)depicts the top view of the weld produced by the narrow pyramid(pin 6 in Fig.19(a)).It has to be noted that the width of this weld is very wide if we compare it with the welds obtained by the conical or cylindrical pins.The reason is that the weld width produced by the square-shaped pin is determined by the diagonal of the square,not by its side.The second important point is that such a pin is not a body of revolution and hence provides better stir of the plasticized material in the joint.But if we compare the Nl(S)plots for the pyramids of different width(curves 6 and 7 in Fig.19(a))we can conclude that to produce the best weld an optimal ratio of the pyramid width and height should exist.

To analyze the peculiarities of the material flow along the plate width during friction stir welding we colored all the automata according to their initial horizontal position(along axis Z).For this purpose,we also used the special pins with additional“wings”(2,3).The final distributions of the stirred automata in the welds obtained by three conical pins are shown in Fig.21.The results demonstrate no significant role of the “wings”on the material flow in the plate width direction.From the other side,the experiments clearly show a marked flow in this direction in the vicinity of the pin[3,10,11].This discrepancy in the experimental evidence and our modeling results can be explained by the assumption that the main role in the flow of the material in the plate width direction during FSW belongs tothe pin shoulder that provides awide area of stirred material in the top of the plate and substantial gradient of stirred material along the plate width direction.

The final point in the 3D simulation of FSW is a study of additional vibrations applied tothe pin during the joining process in the same manner as discussed for the 2D case above.The simulation results for 3D and 2D showed that additional vibration applied perpendicularly to the direction of welding produces much less effect comparing to the longitudinal direction.That is why further we will discuss the results obtained with the vibration applied along axis Y.The plots Nl(S)for different vibration frequencies are shown in Fig.22.For comparison,this figure also contains the plot for the case of no vibration.The power of the vibrations was the same Dus=15μm.

From the presented data one can conclude that the positive effect on the weld quality has vibrations of higher frequencies.For example,the vibration withνus=15Hz resulted in more defects in the weld and made the joining process to be unstable.From the other side,vibration withνus=66Hz allowed to enhance the weld quality.Varying of the vibration amplitude Dusin the range from 5 up to 100μm showed that there was the optimal value of about 30μm that allowed us to get the best weld characterized by the minimal inclination of the plot Nl(S).Thus,the conclusion,which may be drawn from the 3D simulations,that there are the optimal parameters of ultrasound vibration which allow producing the better weld quality is also in good agreement with the results of 2D simulations.

6.Conclusions

Computer simulation using movable cellularautomaton method was performed to theoretically study the peculiarities of materialflow in friction stir welding of duralumin plates.First,we studied the influence of the welding regimes on the material transfer and stir,as well as temperature fields in the welded joints in the 2D statement.The simulation results showed that for the considered model system the optimal values of the ratio of the rotational velocity to the welding speed Vrot/Vtransranged within the interval of 20-40,which provides sufficient material stir and transfer to form a welded joint with a minimum number of defects.The use of FSW regimes in the specified range allows avoiding significant overheating of the joining materials as well.Then the application of the additional ultrasonic impact to the rotating pin was analyzed.The simulations showed that additional ultrasonic vibrations of the special amplitude and frequency can reduce the weld porosity without the significant increase in the weld width.

Based on the 2D simulation results obtained,a 3D model of FSW using movable cellular automaton method is developed.The obtained 3D simulation results allow us to make the following conclusions:(i)the optimal ratio Vrot/Vtransallows transporting of the welded material around the pin several times and producing the joint of high quality;(ii)using the pins of different shape(cylinder,cone,pyramid)without a shoulder results just in small scatter of displacements of the plasticized material in the workpiece thickness direction;(iii)applying additional ultrasonic vibration to the pin may lead to better stir of the welded material behind the pin.

Acknowledgements

The work was carried out in the framework of the Russian Fundamental Research Program of the State Academies of Sciences for 2013-2020(Priority direction III.23).