人工明渠突发水质污染预测模型研究

刘波波，申烨红，雷晓辉

(1.陕西省引汉济渭工程建设有限公司，陕西 西安 710010；2. 中国水利水电科学研究院，北京 100038)

近年来，为解决我国水量分布不均的问题，国内兴建了各种类型的调水工程[1- 2]。其中，人工明渠以其施工方便、成本较低成为被广泛应用的工程形式，特别是在一些长距离调水工程中，多采用人工明渠为主、结合其他形式的水工建筑物进行远距离调水。如我国兴建的南水北调中线工程，全线基本为明渠自流输水。但是明渠开放式的特点，易受自然环境及人为因素影响，加之沿线控制建筑物和交叉建筑物众多，存在各类突发水污染事件隐患。突发水污染事件具有很强的不确定性，且危害大，对水质污染预测和应急处理的要求很高。为了能够较好地模拟污染物的归趋特点，为突发水质污染应急处理提供辅助决策。本文结合人工明渠特点，对突发水质污染事件进行预测研究。

水质模型是根据物质守恒定律，用数学的语言和方法描述参加水循环的水体中水质组分所发生的物理、化学、生物等方面的变化，研究它们之间的相互关系和内在规律的数学模型[3]。针对明渠输水工程突发污染事件，国内外学者开展了一系列研究[4- 6]。目前应用最广泛的是WASP水质模型[7]，它是美国国家环保局开发的专业水质模型软件，能够模拟水文动力学、河网一维非恒定流、湖泊和河口三维非恒定流的常规污染物和有毒污染物在水中的迁移和转化规律。国内在明渠水质模拟方面也做了大量的工作，河海大学开发了一套感潮河网水量水质数学模型(Hwqnow)[8]，并应用在改善上海浦东新区河网水环境调水方案的研究中，取得了良好的效果；徐祖信[9]和廖振良[10]建立了上海苏州河水系的水动力和水质模型，对苏州河水系进行了模拟，取得了令人满意的效果；彭虹[11]利用有限体积法构建了一维明渠综合水质模型，成功地应用于汉江部分河段。

本文以南水北调中线工程某典型渠段为例，开展突发水污染事故预测研究，建立一维水力学模型和基于均衡域的水质离散模型。该离散方程物理机理明确，且该水质控制方程推导中考虑了上风因子，对于以对流为主的河道污染物迁移扩散模拟得更精确。在此基础上，对该典型渠段进行水质模拟，为类似工程的突发水污染事件应急调控提供一定的技术支撑。

1 水质模型

1.1 模型概化

选取的渠段长2km，在该段渠道上包含2座节制闸。在模型中，把渠道中的各类建筑物表达为一系列节点，再通过每段渠道把各个节点串联起来。这些节点的长度为选定的空间坐标长度，这样就把渠道概化为由一系列完全混合反应器构成的系统。为了便于建立物质平衡关系，把所有的节点分为6种类型：源头节点、正常节点、分水口上端节点、分水口下端节点、有点源节点、渠道末节点。渠道概化如图1所示。

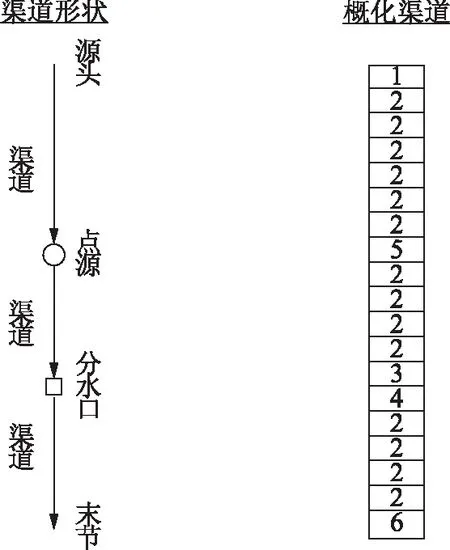
图1 渠道概化

1.2 水质模型中的水力学数值模型

建立水质模型的前提和基础是建立水动力模型，对于长距离输水渠道一般采用描述一维非恒定流的Saint-Venant方程组，表达式如下：

一维St.Venant方程组由连续性方程和动量方程组成：

(1)

(2)

式中，x—空间坐标，m；t—时间坐标，s；A—过流断面面积，m2；Q—流量，m3/s；Z—水位，m；g—重力加速度，m/s2；q—单位长度渠道上的侧向入流流量，m3/s；α—动量修正系数；S0—渠道底坡；Sf—水力坡度。

1.3 水质数值模型

全断面混合距离，考虑反射作用，采用中心排污经验公式

L=0.1VW2/Dt

(3)

式中，L—全混合的均衡域长度，m；V—流速，m/s；Dt—横向离散系数；W—水面宽度，m。

一维瞬时投放示踪实验浓度计算公式为：

(4)

式中，M—总投放物质质量，kg；DL—纵向离散系数；C(x，t)—距离投放源x处t时刻的投放物质浓度。

对于明渠纵向离散系数，本文采用经验公式进行估算。刘亨立(H.Liu)1980年提出的公式为：

(5)

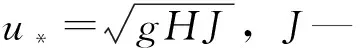
考虑二维瞬时源浓度计算公式：

(6)

式中，x—距离投放点位置纵向距离；y—距离投放点位置横向距离，断面中心处取值为0；Dx—纵向离散系数；Dy—横向离散系数。

考虑到明渠侧壁的反射作用，并假定渠道边壁处浓度达到中心处(断面最大浓度)的95%时，断面污染物质完全混合均匀，故有：

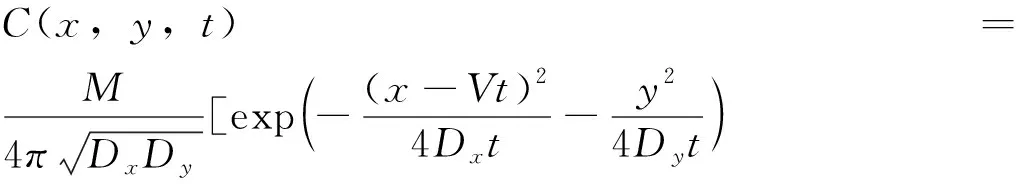
(7)

横向离散系数由经验公式可得：

Dy=0.15h(gRJ)0.5

(8)

式中，h—水深，m；R—水力半径，m；b—水面宽度，m。

2 突发污染计算实例

2.1 突发水质污染工况仿真结果

结合人工明渠突发水污染事件应急调控处置需求，以突发漂浮性油污染事件或可溶性污染事件为例，选取南水北调中线工程某典型渠段开展试验。

假设发生大量有机磷农药泄漏至渠道的突发水污染事件，利用蔗糖(C12H22O11)作为可溶性有机物代替有机磷农药进行示踪试验。蔗糖溶于水后无色，且无臭无毒，不会散发气味，投放后对水体无影响。将1t的蔗糖投入渠道，示踪模拟5t的有机磷农药泄漏至渠道这一突发污染事件。按照设定投放量投放后，经过沿程稀释，选取3个断面为监测点。从上至下分别为1断面，2断面，3断面，3个断面距投放点的距离分别为500、1500、1800m。

试验开始后，每隔1h对各断面的污染物浓度进行监测，每个断面在左、中、右3个位置取水样，将所测污染物浓度的平均值作为该断面的污染物浓度；同时，利用建立的水质模型进行仿真模拟，得出各断面的水力要素和污染物浓度变化过程。模型计算得出的污染物浓度过程线与实测污染物浓度过程线分别如图2—3所示。

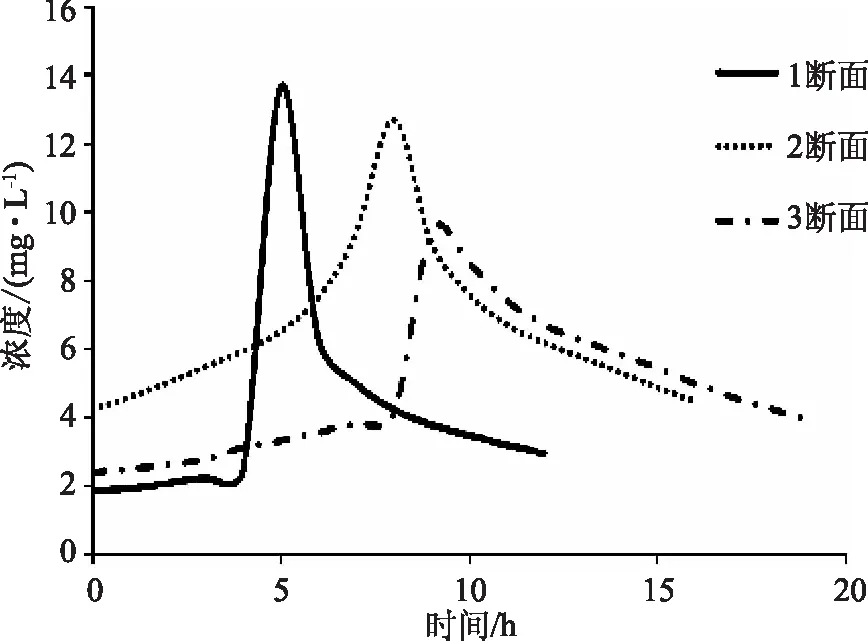
图2 各断面预测浓度过程线

图3 各断面实测浓度过程线

可以看出，在起点发生污染后，随着污染物逐渐向下游扩散，3个断面的污染物浓度依次达到了峰值，且峰值浓度依次降低。随着监测和模拟时间的延长，污染物浓度最后逐渐将至初始值。预测值和实测值显示了相同的趋势和结果。

为检验模型模拟的精确程度，将各断面污染物浓度的实测值和预测值进行比对，如图4—7所示。

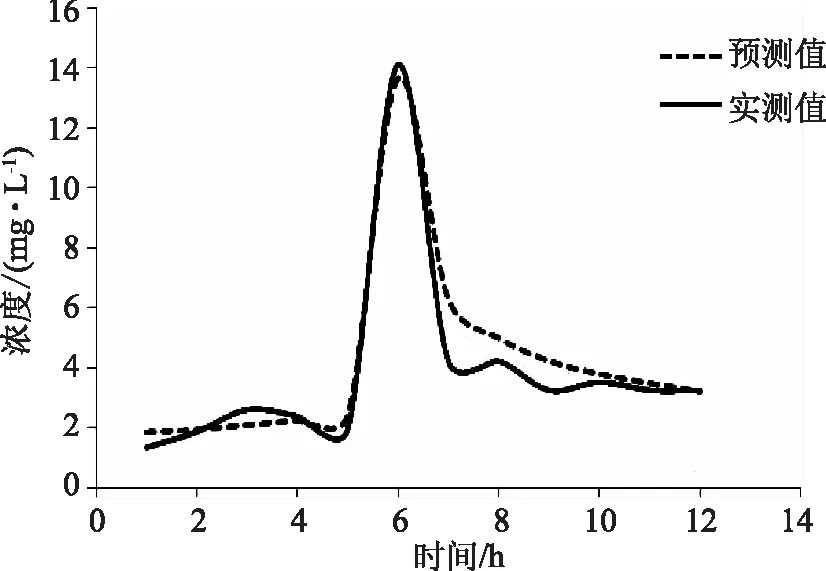
图4 1断面浓度变化过程曲线

图5 2断面浓度变化过程线

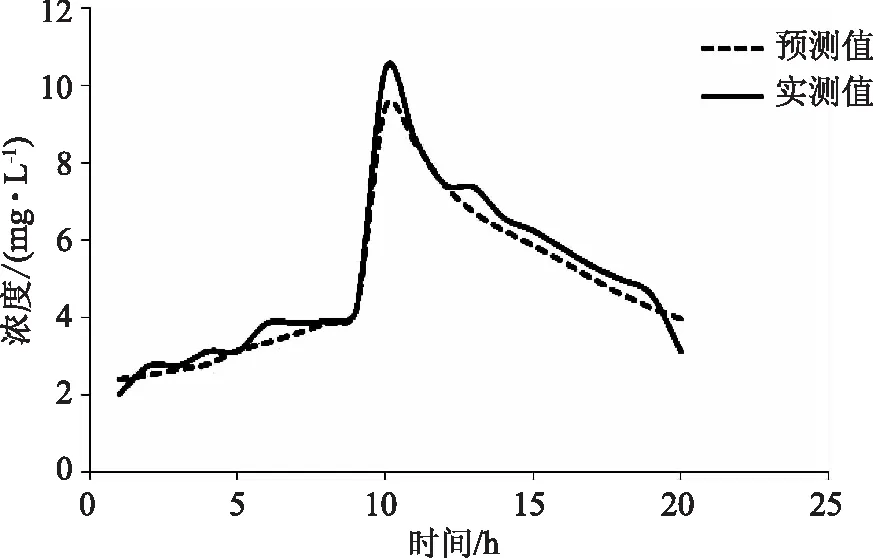
图6 3断面浓度变化过程线

图7 不同时刻渠道污染物总量误差

由图4—6可以看出，预测值和实测值的曲线变化趋势相同，线型基本吻合，误差不超过2mg/L。图7为用模型计算的各时刻的污染物浓度求得的渠道污染物总量与实测计算的相对误差，可以看出，相对误差不超过0.02%，说明模型模拟的结果较为精确。图中相对误差随时间推移逐渐变大，是因为随着污染物不断地扩散稀释，测得的污染物浓度偏差较大导致。

各断面水力要素计算及模型系数选择对比见表1—2。

2.2 结果分析

(1)由表2可以看出，第一个监测断面距离投放点为500m，大于完全混合均匀的均衡域长度410m。从而可以判断，从第一断面开始，在渠道中投放的蔗糖已混合均匀，故采用一维水质模型计算完全可以满足精度要求。

表1 各断面水力要素汇总表

表2 各断面水质汇总表

(2)比较表1和表2，可以看出实测的浓度峰值到达时间与模型计算的峰值到达时间基本一致。模型计算的峰值浓度与实测的浓度峰值相对误差最大为9.38%，最小为1.48%，模拟较为准确。

(3)通过比较模拟值和实测值，峰值浓度前后出现较大偏差，且局部出现了小波峰，产生这种现象的原因可能是：投放蔗糖溶液时未完全做到瞬时投放；采水样时由于仅在表层取水，且渠道横向紊动较大，导致浓度峰值变化不均。

(4)3个断面通过实测计算的纵向离散系数有所差别，但都和通过经验公式计算所得的1.52较为接近；对3个断面纵向离散系数加权平均，得到试验渠道纵向离散系数DL估算值为1.46，所以直接利用通过经验公式所得的离散系数也比较合理，可以大大精简计算。

3 结论

(1)本文针对研究渠段的特点和设计的水污染试验，建立了基于一维圣维南方程组和均衡域的水质离散模型。研究表明，模型计算的结果与各项试验实测数据吻合较好，所建立的模型可以较准确地模拟污染物的扩散过程，且能较准确地预测各断面的浓度峰值和达到峰值的时间，为长距离输水工程突发水污染事件时的应急处置提供辅助决策支持。

(2)本文工作仅进行了一维建模研究，尚存在不足之处，如对于长距离大跨度的输水渠道，二维、三维模型更能准确反映污染物在空间扩散的规律；在试验和建模时均未考虑风速等自然因素的影响，而自然因素也会在一定程度上影响污染物的迁移规律。